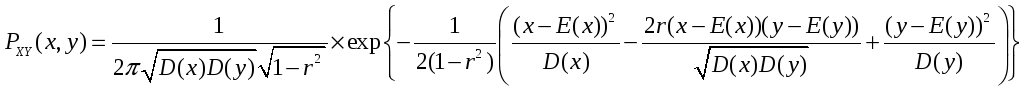Как найти математическое ожидание?
Математическое ожидание случайной величины $X$ (обозначается $M(X)$ или реже $E(X)$) характеризует среднее значение случайной величины (дискретной или непрерывной). Мат. ожидание — это первый начальный момент заданной СВ.
Математическое ожидание относят к так называемым характеристикам положения распределения (к которым также принадлежат мода и медиана). Эта характеристика описывает некое усредненное положение случайной величины на числовой оси. Скажем, если матожидание случайной величины — срока службы лампы, равно 100 часов, то считается, что значения срока службы сосредоточены (с обеих сторон) от этого значения (с тем или иным разбросом, о котором уже говорит дисперсия).
Формула среднего случайной величины
Математическое ожидание дискретной случайной величины Х вычисляется как сумма произведений значений $x_i$ , которые принимает СВ Х, на соответствующие вероятности $p_i$: $$ M(X)=sum_^. $$ Для непрерывной случайной величины (заданной плотностью вероятностей $f(x)$), формула вычисления математического ожидания Х выглядит следующим образом: $$ M(X)=int_<-infty>^ <+infty>f(x) cdot x dx. $$
Пример нахождения математического ожидания
Рассмотрим простые примеры, показывающие как найти M(X) по формулам, введеным выше.
Пример 1. Вычислить математическое ожидание дискретной случайной величины Х, заданной рядом: $$ x_i quad -1 quad 2 quad 5 quad 10 quad 20 \ p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1 $$
Используем формулу для м.о. дискретной случайной величины: $$ M(X)=sum_^. $$ Получаем: $$ M(X)=sum_^ =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8. $$ Вот в этом примере 2 описано также нахождение дисперсии Х.
Пример 2. Найти математическое ожидание для величины Х, распределенной непрерывно с плотностью $f(x)=12(x^2-x^3)$ при $x in(0,1)$ и $f(x)=0$ в остальных точках.
Используем для нахождения мат. ожидания формулу: $$ M(X)=int_<-infty>^ <+infty>f(x) cdot x dx. $$ Подставляем из условия плотность вероятности и вычисляем значение интеграла: $$ M(X)=int_<-infty>^ <+infty>f(x) cdot x dx = int_<0>^ <1>12(x^2-x^3) cdot x dx = int_<0>^ <1>12(x^3-x^4) dx = \ =left.(3x^4-frac<12><5>x^5) right|_0^1=3-frac<12> <5>= frac<3><5>=0.6. $$
Вычисление математического ожидания онлайн
Как найти математическое ожидание онлайн для произвольной дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку «Вычислить».
- Калькулятор покажет вычисленное математическое ожидание $M(X)$.
Видео. Полезные ссылки
Видеоролики: что такое среднее (математическое ожидание)
Если вам нужно более подробное объяснение того, что такое мат.ожидание, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Полезные ссылки
Что еще может пригодиться? Например, для изучения основ теории вероятностей — онлайн учебник по терверу. Для закрепления материала — еще примеры решений по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
3.3 Математические ожидания и ковариации векторов и матриц
3.3. Математические ожидания и ковариации векторов и матриц
При работе с линейными моделями удобно представлять данные в виде векторов или матриц. Элементы некоторых векторов или матриц статистических линейных моделей являются случайными переменными. Определение случайной переменной было дано. Значение этой переменной зависит от случайного результата опыта.
В этой книге рассматривается такой тип векторов случайных переменных отклика, элементы которого могут быть коррелированы, а влияющие на них переменные являются контролируемыми и неслучайными. В конкретной линейной модели, влияющие на отклик переменные, имеют выбранные или полученные в результате расчёта детерминированные значения. Таким образом, в рассматриваемых линейных моделях имеются два вектора случайных переменных:
у= 

Значения i-й переменной уi (i=1, 2, …, n) отклика наблюдаются в результате проведения i-го опыта эксперимента, а значения переменной ei случайной ошибки не наблюдаются, но могут оцениваться по наблюдаемым значениям переменной отклика и значениям влияющих на неё переменных.
При рассмотрении линейных моделей широко используются векторы и матрицы случайных переменных, поэтому в первую очередь для них необходимо обобщить идеи математического ожидания, ковариации и дисперсии.
Математическое ожидание вектора у размеров пх1 случайных переменных y1, y2, . уп определяется как вектор их ожидаемых значений:
Е(у)=Е


Рекомендуемые файлы
где E(уi)=yi получается в виде E(уi)=
Если х и у — векторы случайных переменных размеров пх1, то, в силу (3.3.1) и (3.2.7), математическое ожидание их суммы равно сумме их математических ожиданий:
Пусть уij (i=1, 2, . m; j=1, 2, . п) набор случайных переменных с ожидаемыми значениями E(уij). Выражая случайные переменные и их математические ожидания в матричной форме, можно определить общий оператор математического ожидания матрицы Y=(yij) размеров mхп следующим образом:
Определение 3.3.1. Математическое ожидание матрицы Y случайных переменных равно матрице математических ожиданий её элементов
По аналогии с выражением (3.3.1), ожидаемые значения матрицы Y случайных переменных представляются в виде матрицы ожидаемых значений:
E(Y)=

Вектор можно рассматривать как матрицу, следовательно, определение 3.3.1 и следующая теорема справедливы и для векторов.
Теорема 3.3.1. Если матрицы А=(аij) размеров lхm, B=(bij) размеров nхp, С=(cij) размеров lхp – все имеют элементами постоянные числовые значения, а Y – матрица размеров mхn случайных переменных, то
Доказательство дано в книгах [Себер (1980) стр.19; Seber, Lee (2003) стр.5]
Там же доказывается, что, если матрицы A и В размеров mхn, элементами которых являются постоянные числовые значения, а х и у — векторы случайных переменных размеров пх1, то
Если f(Y) – линейная функция матрицы Y, то её ожидаемое значение находится по формуле Е[f(Y)]=f[Е(Y)] [Boik (2011) cтр.134]. Например, если матрицы А размеров рхm, B размеров пхр и С размеров рхр — все имеют элементами постоянные числовые значения, а матрица Y размеров тхп случайных переменных, то
Ковариации и дисперсии
Аналогичным образом можно обобщить понятия ковариации и дисперсии для векторов. Если векторы случайных переменных х размеров mх1 и у размеров nх1, то ковариация этих векторов определяется следующим образом.
Определение 3.3.2. Ковариацией векторов х и у случайных переменных является прямоугольная матрица ковариаций их элементов
Теорема 3.3.2. Если случайные векторы х и у имеют векторы математических ожиданий E(x)=x и Е(у)=y, то их ковариация
Применим эту теорему для нахождения матрицы ковариаций векторов х размеров 3х1 и у размеров 2х1
=E
=Е
=
=
E[(y–y)(y–y) T ]=
Дисперсии s11, s22, . sпп переменных y1, y2, . уп и их ковариации sij, для всех i≠j, могут быть удобно представлены матрицей дисперсий и ковариаций, которая иногда называется ковариационной матрицей и обозначается прописной буквой S строчной s:
S=D(у)= 
В матрице S i-я строка содержит дисперсию переменной уi и её ковариации с каждой из остальных переменных вектора у. Чтобы быть последовательными с обозначением sij, используем для дисперсий sii=si 2 , где i =1, 2, . n. При этом дисперсии расположены по диагонали матрицы S и ковариации занимают позиции за пределами диагонали. Отметим различие в значении между обозначениями D(у)=S для вектора и С(уi, уj)=sij для двух переменных.
Матрица S дисперсий и ковариаций симметричная, так как sij=sji [см. (3.2.9)]. Во многих приложениях полагается, что матрица S положительно определённая. Это обычно верно, если рассматриваются непрерывные случайные переменные, и между ними нет линейных зависимостей. Если между переменными есть линейные зависимости, то матрица S будет неотрицательно определённой.
Для примера найдём матрицу дисперсий и ковариаций вектора у размеров 3х1
=E
=E
=
=
Как следует из определения 3.3.3,
что после подобного сделанному в (3.2.4) преобразованию приводится к выражению
Последние два выражения являются естественным обобщением одномерных результатов данных выражениями (3.2.2) и (3.2.4).
Пример 3.3.1. Если а — какой-либо вектор числовых значений тех же размеров пх1, что и вектор у, то
Напомним, что симметричная матрица А является положительно определенной, если для всех векторов у≠0 квадратичная форма у Т Ау>0. В дальнейшем будет использоваться часто следующая теорема.
Теорема 3.3.3. Если у — вектор случайных переменных, в котором ни одна из переменных не является линейной комбинации остальных, то есть, нет вектора а≠0 и числа b таких, что а Т у=b для любого у, то D(у)=S — положительно определенная матрица.
Доказательство этой теоремы дано в [Себер (1980) стр.22].
Обобщенная дисперсия и нормированный вектор
Матрица S содержит дисперсии и ковариации всех п случайных переменных вектора у и всесторонне представляет полную их вариацию. Обобщённой мерой, характеризующей вариацию случайных переменных вектора у, может служить определитель матрицы S:
Обобщенная дисперсия =det(S). (3.3.9)
В качестве статистики обобщённой дисперсии используется обобщённая выборочная дисперсия, определяемая детерминантом матрицы S=Y T (I–Е/n)Y/(n–1) вариаций и ковариаций выборочных значений переменных вектора у, представленных матрицей Y=[y1, y2, …, yk], где её столбцы составлены из векторов значений переменных вектора у [Rencher, Christensen (2012) стр.81]:
Обобщенная выборочная дисперсия =det(S). (3.3.10)
Если det(S) малый, то значения переменных вектора у располагаются ближе к их усреднённым значениям вектора 
Для получения полезной меры разности между векторами у и y необходимо учитывать дисперсии и ковариации переменных вектора у. Как для одной нормированной случайной переменной, получаемой по формуле z=(у–y)/s и имеющей среднее равное 0 и дисперсию равную 1, нормированная разность между векторами у и y определяется в виде
Использование матрицы S –1 в этом выражении нормирует (трансформирует) переменные вектора у так, что нормированные переменные имеют средние равные 0 и дисперсии равные 1, а также становятся и некоррелированными. Это получается потому, что матрица S положительно определённая. По теореме П.6.5 её обратная матрица тоже положительно определённая. В силу (П.12.18), матрица S –1 =S –1/2 S –1/2 . Отсюда
где z=S –1/2 (у–y) — вектор нормированных случайных переменных. Математическое ожидание вектора z получается
и его дисперсия
Следовательно, по пункту 2 теоремы 4.5.2 следующей главы вектор S –1/2 (у–y) имеет нормальное распределение N(0, I).
Для нормированной разности, как параметра, есть соответствующая статистика, а именно, выборочная нормированная дистанция, определяемая формулой (у–






Математическое ожидание
Математическое ожидание — это ожидаемый результат от какого-то действия.
Например, можно рассчитать ожидаемую стоимость инвестиции в определённый момент в будущем. Рассчитывая математическое ожидание перед тем, как инвестировать, можно выбрать наилучший сценарий который, по мнению инвестора, даст наилучший результат.
Случайная величина может быть двух типов:
- Дискретной: число возможных значений X — это числимое конечное или бесконечное множество точек; пример: количество дефектных устройств в производстве фабрики.
- Непрерывной: X может принимать любое значение в заданном диапазоне; пример: концентрация углекислого газа в воде.
Математическое ожидание дискретной случайной величины рассчитывается этой формулой:
Математическое ожидание дискретной случайной величины рассчитывается:
1. Сначала нужно умножить каждое из возможных результатов на свою вероятность (например: вероятность, что выпадет «1» — 1/6, «2» — 1/3, значит умножаем 1 на 1/6, 2 на 1/3, и т.д.),
2. Затем суммируем все эти значения (1 × 1/6 + 2 × 1/3 и т.д.).
Для непрерывной случайной величины используется эта формула:
В этом случае рассчитывается интеграл в заданном интервале.
Примеры вычисления математического ожидания
- если в задаче даётся таблица с данными, то перемножаем каждое событие на его вероятность и потом всё складываем;
- если в задаче дают функцию с заданным интервалом, то вычисляем интеграл с этим интервалом.
Пример 1
Вычислить математическое ожидание дискретной случайной величины Х со следующими данными:
| xi | −1 | 1 | 2 | 3 | 4 |
| pi | 0,1 | 0,2 | 0,3 | 0,1 | 0,3 |
Используется формула для дискретной случайной величины:
M(X) = ∑ xi×pi = −1×0,1+ 1×0,2 + 2×0,3 + 3×0,1 + 4×0,3 = −0,1 + 0,2 + 0,6 + 0,3 + 1,2 = 2,2
Пример 2
Найти математическое ожидание для величины Х, распределённой непрерывно с плотностью f(x) = 2x, при x∈(0,1) и f(x) = 0 в остальных точках.
Используется формула для непрерывной случайной величины:
Пример 3
Вычислить математическое ожидание дискретной случайной величины Х со следующими данными:
| xi | 1 | 2 | 3 | 4 | 5 |
| pi | 0,3 | 0,3 | 0,1 | 0,1 | 0,2 |
Используется формула для дискретной случайной величины:
M(X) = ∑ xi×pi = 1×0,3 + 2×0,3 + 3×0,1 + 4×0,1 + 5×0,2 = 0,3 + 0,6 + 0,3 + 0,4 + 1 = 2,6
Пример 4
Найти математическое ожидание для величины Х, распределённой непрерывно с плотностью f(x) = (1/10).(3x²+1), при x∈(0,2) и f(x) = 0 в остальных точках.
Используется формула для непрерывной случайной величины:
http://studizba.com/lectures/47-matematika/680-statisticheskie-metody-eksperimentalnyh-issledovaniy/13066-33-matematicheskie-ozhidaniya-i-kovariacii-vektorov-i-matric.html
http://www.uznaychtotakoe.ru/matematicheskoe-ozhidanie/
Савельев Ф. Г.
Гр. 2351
Вариант 19.
Дано:
-
Вычисление вектора мат. Ожиданий и
ковариационных характеристик С.В.
Сначала найдём неизвестную константу.
Для этого вычислим плотность распределения
одной из компонент случайного вектора
с учётом неизвестной константы C
и приравняем её к единице.
.
Найдём вектор математических ожиданий
Имеем:
.
Плотность распределения
:
Плотность распределения
:
Отсюда,
—
вектор мат. ожиданий.
Ковариационную матрицу мы можем найти
двумя способами
1-ый способ. Ковариационная матрица
– это матрица, обратная матрице
квадратичной формы.
Матрица квадратичной формы:
;
Матрица ковариации:

2-ой способ. Найдем первый и четвертый
элемент матрицы ковариации – это
дисперсии компонент случайного вектора
x и y
соответственно.
,
Остается найти второй и третий члены
матрицы. Они, как известно, равны между
собой и вычисляются по формуле:
.
Найдем
.
Тогда второй и третий элементы будут
равны:
.
Имеем матрицу ковариации:
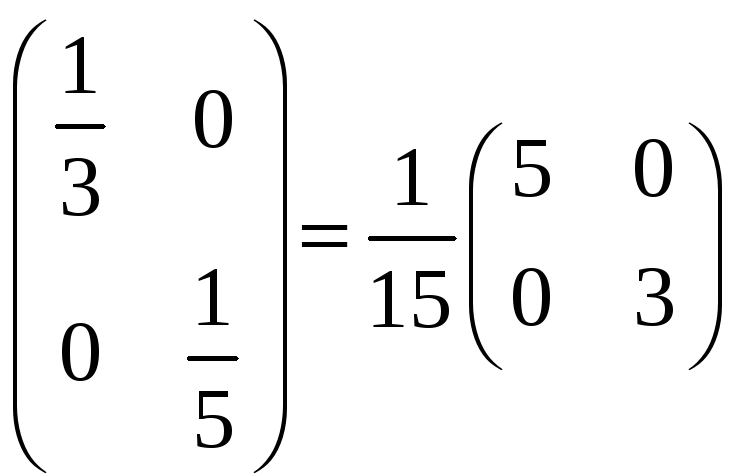
что полностью совпало с вычисленным
первым способом.
-
Найти ортогональное преобразование,
переводящее соответствующий центрированный
случайный вектор в вектор с независимыми
компонентами.
Преобразование будет называться
ортогональным, если его матрица будет
ортогональна т. е.
Тогда само преобразование можно описать
формулой
— матрица
— вектор при этом матрица
должна быть ортогональной.
Однако нам в задании уже дана плотность
с независимыми компонентами, следовательно
для перевода данного случайного вектора
в центрированный вектор необходим лишь
сдвиг. Опишем общий вид данного
преобразования.
Матрица
— матрица перехода от стандартного
базиса к базису собственных векторов
нашей матрицы квадратичной формы.
Матрица квадратичной формы
уже диагональная и собственные числа
равны, соответственно,
Матрица перехода будет
— единичная матрица. Эта матрица
ортогональна, следовательно, ортогонально
и преобразование. Для центрирования
данного случайного вектора необходимо
просто отнять столбец математических
ожиданий данных компонент.
Произведём первую замену. Вместе
,
подставляем новые координаты

Тогда квадратичная форма будет следующей
Якобиан такой замены будет равен 1
Следовательно, после такой замены,
плотность случайного вектора принимает
вид
Данный вектор центрирован (математическое
ожидание обоих компонент равно 0), имеет
независимые друг от друга компоненты
и получен ортогональным преобразованием.
Из такого вектора легко получить
стандартный нормальный вектор. Достаточно
сделать ещё одну замену. Вместо
,
ставим
На диагонали всегда будут находиться
члены вида
.
Якобиан такой замены также можно очень
просто посчитать
И умножив плотность распределения
т. е. компонент предыдущей замены получим
плотность распределения стандартного
и центрированного вектора.
4. Вычислить характеристики совместного
распределения с.в.
и
записать его плотность.
Математические ожидания мы находим,
используя свойство его линейности.
Пусть
,
тогда
,
.
Находим новые дисперсии, используя
свойства линейности для независимых
компонент.
Для заданного случайного вектора
компоненты уже независимы, следовательно,
мы можем найти дисперсию так:
Из ранее найденного имеем:
Тогда можно вычислить
.
Аналогично, имеем для дисперсии Y:
.
Вычислим матрицу ковариации
,
Надо вычислить ковариации новых компонент
вектора.
.
для наших независимых компонент равно
0.
Отсюда, матрица ковариации в явном виде:
.
Записываем плотность нового случайного
вектора
где

Подставив все значения, получим:

Для проверки распределения составим
матрицу квадратичной формы,
Возведем ее в (-1)-ую степень
получили матрицу ковариации, что
показывает верность наших расчетов.
Материал из MachineLearning.
Перейти к: навигация, поиск
Математическое ожидание — мера среднего значения случайной величины в теории вероятностей. В зарубежной литературе обозначается через (например, от англ. Expected value или нем. Erwartungswert), в русской
(возможно, от англ. Mean value).
Содержание
- 1 Определение
- 2 Основные формулы для математического ожидания
- 2.1 Математическое ожидание дискретного распределения
- 2.1.1 Математическое ожидание целочисленной величины
- 2.2 Математическое ожидание абсолютно непрерывного распределения
- 2.1 Математическое ожидание дискретного распределения
- 3 Математическое ожидание случайного вектора
- 4 Математическое ожидание преобразования случайной величины
- 5 Простейшие свойства математического ожидания
- 6 Дополнительные свойства математического ожидания
- 7 Примеры
- 8 Литература
Определение
Пусть задано вероятностное пространство и определённая на нём случайная величина
. Тогда, если существует интеграл Лебега от
по пространству
, то он называется математическим ожиданием, или средним значением, и обозначается
или
.
Основные формулы для математического ожидания
- Если
— функция распределения случайной величины, то её математическое ожидание задаётся интегралом Лебега — Стилтьеса:
-
.
Математическое ожидание дискретного распределения
- Если
— дискретная случайная величина, имеющая распределение
-
,
то прямо из определения интеграла Лебега следует, что
-
.
Математическое ожидание целочисленной величины
- Если
— положительная целочисленная случайная величина (частный случай дискретной), имеющая распределение вероятностей
то её математическое ожидание может быть выражено через производящую функцию последовательности
как значение первой производной в единице: . Если математическое ожидание
бесконечно, то
и мы будем писать
Теперь возьмём производящую функцию последовательности «хвостов» распределения
Эта производящая функция связана с определённой ранее функцией свойством:
при
.
Из этого по теореме о среднем (формуле конечных приращений) следует, что математическое ожидание равно просто значению этой функции в единице:
Математическое ожидание абсолютно непрерывного распределения
- Математическое ожидание абсолютно непрерывной случайной величины, распределение которой задаётся плотностью
, равно
-
.
Математическое ожидание случайного вектора
Пусть — случайный вектор. Тогда по определению
-
,
то есть математическое ожидание вектора определяется покомпонентно.
Математическое ожидание преобразования случайной величины
Пусть — борелевская функция, такая что случайная величина
имеет конечное математическое ожидание. Тогда для него справедлива формула:
-
,
если имеет дискретное распределение;
-
,
если имеет абсолютно непрерывное распределение.
Если распределение случайной величины
общего вида, то
-
.
В специальном случае, когда , Математическое ожидание
называется
-тым моментом случайной величины.
Простейшие свойства математического ожидания
- Математическое ожидание числа есть само число.
-
-
-
— константа;
- Математическое ожидание линейно, то есть
-
-
,
-
- где
— случайные величины с конечным математическим ожиданием, а
— произвольные константы;
-
-
;
-
- Математическое ожидание не зависит от поведения случайной величины на событии вероятности нуль, то есть если
почти наверное, то
-
-
.
-
- Математическое ожидание произведения двух независимых случайных величин
равно произведению их математических ожиданий
-
-
.
-
Дополнительные свойства математического ожидания
- Неравенство Маркова.
Пусть случайная величина определена на вероятностном пространстве
, и её математическое ожидание конечно. Тогда
,
где .
- Теорема Леви о монотонной сходимости.
Пусть — монотонная последовательность неотрицательных почти наверное интегрируемых случайных величин. Тогда
-
.
- Теорема Лебега о мажорируемой сходимости.
Пусть есть сходящаяся почти наверное последовательность случайных величин: почти наверное. Пусть в дополнение существует интегрируемая случайная величина
, такая что
почти наверное. Тогда случайные величины
интегрируемы и
-
.
- Тождество Вальда.
Пусть — независимые одинаково распределенные случайные величины.
— также является случайной величиной имеющей дискретное распределение и принимающая положительные целые значения. Далее,
и
должны иметь конечное математическое ожидание и
должно быть независимым от
. Тогда
-
.
- Лемма Фату.
Пусть есть неотрицательная последовательность интегрируемых случайных величин . Тогда выполняется следующее неравенство для нижних пределов:
-
.
Примеры
- Пусть случайная величина имеет дискретное равномерное распределение, то есть
Тогда её математическое ожидание
равно среднему арифметическому всех принимаемых значений.
-
.
- Пусть случайная величина
имеет стандартное распределение Коши. Тогда
-
,
то есть математическое ожидание не определено.
Литература
- В.Феллер Глава XI. Целочисленные величины. Производящие функции // Введение в теорию вероятностей и её приложения = An introduction to probability theory and its applicatons, Volume I second edition. — 2-е изд. — М.: Мир, 1964. — С. 270—272.
3.3. Математические ожидания и ковариации векторов и матриц
При работе с линейными моделями удобно представлять данные в виде векторов или матриц. Элементы некоторых векторов или матриц статистических линейных моделей являются случайными переменными. Определение случайной переменной было дано. Значение этой переменной зависит от случайного результата опыта.
В этой книге рассматривается такой тип векторов случайных переменных отклика, элементы которого могут быть коррелированы, а влияющие на них переменные являются контролируемыми и неслучайными. В конкретной линейной модели, влияющие на отклик переменные, имеют выбранные или полученные в результате расчёта детерминированные значения. Таким образом, в рассматриваемых линейных моделях имеются два вектора случайных переменных:
у=

Значения i-й переменной уi (i=1, 2, …, n) отклика наблюдаются в результате проведения i-го опыта эксперимента, а значения переменной ei случайной ошибки не наблюдаются, но могут оцениваться по наблюдаемым значениям переменной отклика и значениям влияющих на неё переменных.
При рассмотрении линейных моделей широко используются векторы и матрицы случайных переменных, поэтому в первую очередь для них необходимо обобщить идеи математического ожидания, ковариации и дисперсии.
Математические ожидания
Математическое ожидание вектора у размеров пх1 случайных переменных y1, y2, …, уп определяется как вектор их ожидаемых значений:
Е(у)=Е


Рекомендуемые материалы
где E(уi)=yi получается в виде E(уi)=
Если х и у — векторы случайных переменных размеров пх1, то, в силу (3.3.1) и (3.2.7), математическое ожидание их суммы равно сумме их математических ожиданий:
Е(х+у)=Е(х)+Е(у). (3.3.2)
Пусть уij (i=1, 2, …, m; j=1, 2, …, п) набор случайных переменных с ожидаемыми значениями E(уij). Выражая случайные переменные и их математические ожидания в матричной форме, можно определить общий оператор математического ожидания матрицы Y=(yij) размеров mхп следующим образом:
Определение 3.3.1. Математическое ожидание матрицы Y случайных переменных равно матрице математических ожиданий её элементов
E(Y)=[E(yij)].
По аналогии с выражением (3.3.1), ожидаемые значения матрицы Y случайных переменных представляются в виде матрицы ожидаемых значений:
E(Y)=

Вектор можно рассматривать как матрицу, следовательно, определение 3.3.1 и следующая теорема справедливы и для векторов.
Теорема 3.3.1. Если матрицы А=(аij) размеров lхm, B=(bij) размеров nхp, С=(cij) размеров lхp – все имеют элементами постоянные числовые значения, а Y – матрица размеров mхn случайных переменных, то
E(AYB+C)=AE(Y)B+C. (3.3.4)
Доказательство дано в книгах [Себер (1980) стр.19; Seber, Lee (2003) стр.5]
□
Там же доказывается, что, если матрицы A и В размеров mхn, элементами которых являются постоянные числовые значения, а х и у — векторы случайных переменных размеров пх1, то
E(Aх+Bу)=AE(х)+BE(у).
Если f(Y) – линейная функция матрицы Y, то её ожидаемое значение находится по формуле Е[f(Y)]=f[Е(Y)] [Boik (2011) cтр.134]. Например, если матрицы А размеров рхm, B размеров пхр и С размеров рхр — все имеют элементами постоянные числовые значения, а матрица Y размеров тхп случайных переменных, то
E[след(AYB+C)]=след[E(AYB+C)], так как след матрицы — линейный оператор
=след[AE(Y)B+C], так как AYB+C — линейная функция матрицы Y
=след[AE(Y)B]+след(C). (3.3.5)
Ковариации и дисперсии
Аналогичным образом можно обобщить понятия ковариации и дисперсии для векторов. Если векторы случайных переменных х размеров mх1 и у размеров nх1, то ковариация этих векторов определяется следующим образом.
Определение 3.3.2. Ковариацией векторов х и у случайных переменных является прямоугольная матрица ковариаций их элементов
C(х, у)=[C(хi, уj)].
Теорема 3.3.2. Если случайные векторы х и у имеют векторы математических ожиданий E(x)=x и Е(у)=y, то их ковариация
C(х, у)=E[(x–x)(y–y)T].
Доказательство:
C(х, у)=[C(хi, уj)]
={E[(хi–xi)(yj–yj)]} [в силу (3.2.9)]
=E[(x–x)(y–y)T]. [по определению 3.3.1]
□
Применим эту теорему для нахождения матрицы ковариаций векторов х размеров 3х1 и у размеров 2х1
C(х, у)=E[(x–x)(y–y)T]
=E
=Е
=
Определение 3.3.3. Если х=у, то матрица ковариаций C(у, у) записывается в виде D(у)=E[(y–y)(y–y)T] и называется матрицей дисперсий и ковариаций вектора у. Таким образом,
D(у)=E[(y–y)(y–y)T]=[C(уi, уj)]
=
А так как C(уi, уj)=C(уj, уi), то матрица (3.3.4) симметричная и квадратная.
Матрица дисперсий и ковариаций вектора у представляется в виде ожидаемого значения произведения (y–y)(y–y)T. В силу (П.2.13), произведение (yi–yi)(yj–yj) является (ij)-м элементом матрицы (y–y)(y–y)T. Таким образом, в силу (3.2.9) и (3.3.4), математическое ожидание E[(yi–yi)(yj–yj)]=sij является (ij)-м элементом Е[(y–y)(y–y)T]. Отсюда
E[(y–y)(y–y)T]=
Дисперсии s11, s22, …, sпп переменных y1, y2, …, уп и их ковариации sij, для всех i≠j, могут быть удобно представлены матрицей дисперсий и ковариаций, которая иногда называется ковариационной матрицей и обозначается прописной буквой S строчной s:
S=D(у)=
В матрице S i-я строка содержит дисперсию переменной уi и её ковариации с каждой из остальных переменных вектора у. Чтобы быть последовательными с обозначением sij, используем для дисперсий sii=si2, где i =1, 2, …, n. При этом дисперсии расположены по диагонали матрицы S и ковариации занимают позиции за пределами диагонали. Отметим различие в значении между обозначениями D(у)=S для вектора и С(уi, уj)=sij для двух переменных.
Матрица S дисперсий и ковариаций симметричная, так как sij=sji [см. (3.2.9)]. Во многих приложениях полагается, что матрица S положительно определённая. Это обычно верно, если рассматриваются непрерывные случайные переменные, и между ними нет линейных зависимостей. Если между переменными есть линейные зависимости, то матрица S будет неотрицательно определённой.
Для примера найдём матрицу дисперсий и ковариаций вектора у размеров 3х1
D(у)=E[(y–y)(y–y)T]
=E
=E
=
=
Как следует из определения 3.3.3,
D(у)=E[(у–y)(y–y)T], (3.3.7)
что после подобного сделанному в (3.2.4) преобразованию приводится к выражению
D(y)=E(yyT)–yyT. (3.3.8)
Последние два выражения являются естественным обобщением одномерных результатов данных выражениями (3.2.2) и (3.2.4).
Пример 3.3.1. Если а — какой-либо вектор числовых значений тех же размеров пх1, что и вектор у, то
D(y–а)=D(y).
Это следует из того, что yi–ai–E(yi–ai)=yi–ai–E(yi)+ai=yi–E(yi), так что
C(yi–ai, yj–aj)=C(yi, yj).
□
Напомним, что симметричная матрица А является положительно определенной, если для всех векторов у≠0 квадратичная форма уТАу>0. В дальнейшем будет использоваться часто следующая теорема.
Теорема 3.3.3. Если у — вектор случайных переменных, в котором ни одна из переменных не является линейной комбинации остальных, то есть, нет вектора а≠0 и числа b таких, что аТу=b для любого у, то D(у)=S — положительно определенная матрица.
Доказательство этой теоремы дано в [Себер (1980) стр.22].
□
Обобщенная дисперсия и нормированный вектор
Матрица S содержит дисперсии и ковариации всех п случайных переменных вектора у и всесторонне представляет полную их вариацию. Обобщённой мерой, характеризующей вариацию случайных переменных вектора у, может служить определитель матрицы S:
Обобщенная дисперсия =det(S). (3.3.9)
В качестве статистики обобщённой дисперсии используется обобщённая выборочная дисперсия, определяемая детерминантом матрицы S=YT(I–Е/n)Y/(n–1) вариаций и ковариаций выборочных значений переменных вектора у, представленных матрицей Y=[y1, y2, …, yk], где её столбцы составлены из векторов значений переменных вектора у [Rencher, Christensen (2012) стр.81]:
Обобщенная выборочная дисперсия =det(S). (3.3.10)
Если det(S) малый, то значения переменных вектора у располагаются ближе к их усреднённым значениям вектора 
Для получения полезной меры разности между векторами у и y необходимо учитывать дисперсии и ковариации переменных вектора у. Как для одной нормированной случайной переменной, получаемой по формуле z=(у–y)/s и имеющей среднее равное 0 и дисперсию равную 1, нормированная разность между векторами у и y определяется в виде
Нормированная разность =(у–y)ТS–1(у–y). (3.3.11)
Использование матрицы S–1 в этом выражении нормирует (трансформирует) переменные вектора у так, что нормированные переменные имеют средние равные 0 и дисперсии равные 1, а также становятся и некоррелированными. Это получается потому, что матрица S положительно определённая. По теореме П.6.5 её обратная матрица тоже положительно определённая. В силу (П.12.18), матрица S–1=S–1/2S–1/2. Отсюда
(у–y)ТS–1(у–y)=(у–y)ТS–1/2S–1/2(у–y)
=[S–1/2(у–y)]Т[S–1/2(у–y)]
=zТz,
Вам также может быть полезна лекция «Построение формы в ранне многоголосии».
где z=S–1/2(у–y) — вектор нормированных случайных переменных. Математическое ожидание вектора z получается
Е(z)=Е[S–1/2(у–y)]=S–1/2[Е(у)–y]=0
и его дисперсия
D(z)=D[S–1/2(у–y)]=S–1/2D(у–y)S–1/2=S–1/2SS–1/2=S–1/2S1/2S1/2S–1/2=I.
Следовательно, по пункту 2 теоремы 4.5.2 следующей главы вектор S–1/2(у–y) имеет нормальное распределение N(0, I).
Для нормированной разности, как параметра, есть соответствующая статистика, а именно, выборочная нормированная дистанция, определяемая формулой (у–






Математи́ческое ожида́ние — понятие в теории вероятностей, означающее среднее (взвешенное по вероятностям возможных значений) значение случайной величины[1]. Математическое ожидание характеризует распределение вероятностей для случайной величины [math]displaystyle{ X }[/math].
В случае непрерывной случайной величины подразумевается взвешивание по плотности распределения (более строгие определения см. ниже). Математическое ожидание случайного вектора равно вектору, компоненты которого равны математическим ожиданиям компонентов случайного вектора.
Обозначается через [math]displaystyle{ mathbb{E}[X] }[/math][2] (например, от англ. Expected value или нем. Erwartungswert);
в русскоязычной литературе также встречается обозначение [math]displaystyle{ M[X] }[/math] (возможно, от англ. Mean value или нем. Mittelwert, а возможно от «Математическое ожидание»). В статистике часто используют обозначение [math]displaystyle{ mu }[/math].
Для случайной величины, принимающей значения только 0 или 1 математическое ожидание равно [math]displaystyle{ p }[/math] — вероятности «единицы». Математическое ожидание суммы таких случайных величин равно [math]displaystyle{ np }[/math], где [math]displaystyle{ n }[/math] — количество таких случайных величин. При этом вероятности появления определенного кол-ва единиц рассчитываются по биномиальному распределению. Поэтому в литературе, скорее всего, легче найти запись, что мат. ожидание биномиального распределения равно [math]displaystyle{ np }[/math] [3].
Некоторые случайные величины не имеют математического ожидания, например, случайные величины, имеющие распределение Коши.
На практике математическое ожидание обычно оценивается как среднее арифметическое наблюдаемых значений случайной величины (выборочное среднее, среднее по выборке). Доказано, что при соблюдении определенных слабых условий (в частности, если выборка является случайной, то есть наблюдения являются независимыми) выборочное среднее стремится к истинному значению математического ожидания случайной величины при стремлении объема выборки (количества наблюдений, испытаний, измерений) к бесконечности.
Определение
Общее определение через интеграл Лебега
Пусть задано вероятностное пространство [math]displaystyle{ (Omega,mathfrak{A},mathbb{P}) }[/math] и определённая на нём случайная величина [math]displaystyle{ X }[/math]. То есть, по определению, [math]displaystyle{ XcolonOmega to mathbb{R} }[/math] — измеримая функция. Если существует интеграл Лебега от [math]displaystyle{ X }[/math] по пространству [math]displaystyle{ Omega }[/math], то он называется математическим ожиданием, или средним (ожидаемым) значением и обозначается [math]displaystyle{ M[X] }[/math] или [math]displaystyle{ mathbb{E}[X] }[/math].
- [math]displaystyle{ mathbb{E}[X]=intlimits_{Omega}! X(omega), mathbb{P}(domega). }[/math]
Определение через функцию распределения случайной величины
Если [math]displaystyle{ F_X(x) }[/math] — функция распределения случайной величины, то её математическое ожидание задаётся интегралом Лебега — Стилтьеса:
- [math]displaystyle{ mathbb{E}[X]=intlimits_{-infty}^{infty}!x, dF_X(x) }[/math], [math]displaystyle{ x in mathbb R }[/math].
Определение для абсолютно непрерывной случайной величины (через плотность распределения)
Математическое ожидание абсолютно непрерывной случайной величины, распределение которой задаётся плотностью [math]displaystyle{ f_X(x) }[/math], равно
- [math]displaystyle{ mathbb{E}[X]=intlimits_{-infty}^{infty}! x f_X(x), dx }[/math].
Определение для дискретной случайной величины
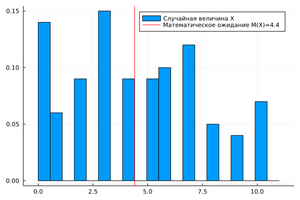
Математическое ожидание случайной величины [math]displaystyle{ X }[/math], принимающей значения [math]displaystyle{ [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10] }[/math] с разной вероятностью. Математическое ожидание [math]displaystyle{ mathbb{E}(X)=4,4 }[/math]
Если [math]displaystyle{ X }[/math] — дискретная случайная величина, имеющая распределение
- [math]displaystyle{ mathbb{P}(X=x_i) = p_i }[/math] , [math]displaystyle{ sumlimits_{i=1}^{infty} p_i = 1 }[/math],
то прямо из определения интеграла Лебега следует, что
- [math]displaystyle{ mathbb{E}[X]=sumlimits_{i=1}^{infty} x_i, p_i }[/math].
Математическим ожиданием дискретной случайной величины называется сумма ряда при условии сходимости ряда.
Математическое ожидание целочисленной величины
- Если [math]displaystyle{ X }[/math] — положительная целочисленная случайная величина (частный случай дискретной), имеющая распределение вероятностей
- [math]displaystyle{ mathbb{P}(X=j) = p_j }[/math] , [math]displaystyle{ j=0,1,dotsc }[/math], [math]displaystyle{ sumlimits_{j=0}^{infty} p_j = 1 }[/math],
то её математическое ожидание может быть выражено через производящую функцию последовательности [math]displaystyle{ {p_i} }[/math]
- [math]displaystyle{ P(s)=sum_{k=0}^infty;p_k s^k }[/math]
как значение первой производной в единице: [math]displaystyle{ mathbb{E}[X] = P'(1) }[/math]. Если математическое ожидание [math]displaystyle{ X }[/math] бесконечно, то [math]displaystyle{ lim_{sto 1}P'(s)=infty }[/math] и мы будем писать [math]displaystyle{ P'(1)=mathbb{E}[X]=infty }[/math]
Теперь возьмём производящую функцию [math]displaystyle{ Q(s) }[/math] последовательности «хвостов» распределения [math]displaystyle{ {q_k} }[/math]
- [math]displaystyle{ q_k=mathbb{P}(Xgt k)=sum_{j=k+1}^infty{p_j} }[/math] , [math]displaystyle{ Q(s)=sum_{k=0}^infty q_k s^k. }[/math]
Эта производящая функция связана с определённой ранее функцией [math]displaystyle{ P(s) }[/math] свойством: [math]displaystyle{ Q(s)=frac{1-P(s)}{1-s} }[/math] при [math]displaystyle{ |s|lt 1 }[/math]. Из этого по теореме о среднем следует, что математическое ожидание равно просто значению этой функции в единице:
- [math]displaystyle{ mathbb{E}[X]=P'(1)=Q(1) }[/math]
Математическое ожидание случайного вектора
Пусть [math]displaystyle{ X=(X_1,dots,X_n)^{top}colonOmega to mathbb{R}^n }[/math] — случайный вектор. Тогда по определению
- [math]displaystyle{ mathbb{E}[X]=(mathbb{E}[X_1],dots,mathbb{E}[X_n])^{top} }[/math],
то есть математическое ожидание вектора определяется покомпонентно.
Математическое ожидание преобразования случайной величины
Пусть [math]displaystyle{ gcolonmathbb{R}to mathbb{R} }[/math] — борелевская функция, такая что случайная величина [math]displaystyle{ Y = g(X) }[/math] имеет конечное математическое ожидание. Тогда для него справедлива формула
- [math]displaystyle{ mathbb{E}left[g(X)right] = sumlimits_{i=1}^{infty} g(x_i) p_i, }[/math]
если [math]displaystyle{ X }[/math] имеет дискретное распределение;
- [math]displaystyle{ mathbb{E}left[g(X)right] = intlimits_{-infty}^{infty}!g(x) f_X(x), dx, }[/math]
если [math]displaystyle{ X }[/math] имеет абсолютно непрерывное распределение.
Если распределение [math]displaystyle{ mathbb{P}^X }[/math] случайной величины [math]displaystyle{ X }[/math] общего вида, то
- [math]displaystyle{ mathbb{E}left[g(X)right] = intlimits_{-infty}^{infty}!g(x), mathbb{P}^X(dx). }[/math]
В специальном случае, когда [math]displaystyle{ g(X) = X^k }[/math], математическое ожидание [math]displaystyle{ mathbb{E}[g(X)] = mathbb{E}[X^k] }[/math] называется [math]displaystyle{ k }[/math]-м моментом случайной величины.
Свойства математического ожидания
- Математическое ожидание числа (не случайной, фиксированной величины, константы) есть само число.
-
- [math]displaystyle{ mathbb{E}[a] = a }[/math]
- [math]displaystyle{ a in mathbb{R} }[/math] — константа;
- Математическое ожидание линейно[4], то есть
-
- [math]displaystyle{ mathbb{E}[aX+bY] = amathbb{E}[X]+bmathbb{E}[Y] }[/math],
- где [math]displaystyle{ X,Y }[/math] — случайные величины с конечным математическим ожиданием, а [math]displaystyle{ a,bin mathbb{R} }[/math] — произвольные константы;
В частности, математическое ожидание суммы (разности) случайных величин равно сумме (соответственно — разности) их математических ожиданий.
- Математическое ожидание сохраняет неравенства, то есть если [math]displaystyle{ 0 leqslant X leqslant Y }[/math] почти наверняка, и [math]displaystyle{ Y }[/math] — случайная величина с конечным математическим ожиданием, то математическое ожидание случайной величины [math]displaystyle{ X }[/math] также конечно, и более того
-
- [math]displaystyle{ 0 leqslant mathbb{E}[X] leqslant mathbb{E}[Y] }[/math].
- Математическое ожидание не зависит от поведения случайной величины на событии вероятности нуль, то есть если [math]displaystyle{ X = Y }[/math] почти наверняка, то
-
- [math]displaystyle{ mathbb{E}[X]=mathbb{E}[Y] }[/math].
- Математическое ожидание произведения двух независимых или некоррелированных[5] случайных величин [math]displaystyle{ X,Y }[/math] равно произведению их математических ожиданий
-
- [math]displaystyle{ mathbb{E}[XY] = mathbb{E}[X]cdot mathbb{E}[Y] }[/math].
Неравенства, связанные с математическим ожиданием
Неравенство Маркова — для неотрицательной случайной величины [math]displaystyle{ Xcolon Omega to mathbb{R}^+ }[/math] определённой на вероятностном пространстве [math]displaystyle{ (Omega, mathcal{F},mathbb{P}) }[/math] с конечным математическим ожиданием [math]displaystyle{ mathbb{E}(X) }[/math] выполняется неравенство:
- [math]displaystyle{ mathbb{P}left(X geqslant aright) leqslant frac{mathbb{E}(X)}{a} }[/math], где [math]displaystyle{ agt 0 }[/math].
Неравенство Йенсена для математического ожидания выпуклой функции от случайной величины. Пусть [math]displaystyle{ (Omega,mathcal{F},mathbb{P}) }[/math] — вероятностное пространство, [math]displaystyle{ XcolonOmegato mathbb{R} }[/math] — определённая на нём случайная величина, [math]displaystyle{ varphicolonmathbb{R} to mathbb{R} }[/math] — выпуклая борелевская функция, такие, что [math]displaystyle{ X, varphi(X) in L^1(Omega,mathcal{F},mathbb{P}) }[/math], то
- [math]displaystyle{ varphi(mathbb{E}(X)) leqslant mathbb{E}(varphi(X)) }[/math].
Теоремы, связанные с математическим ожиданием
- Теорема Леви о монотонной сходимости.
- Теорема Лебега о мажорируемой сходимости: пусть есть сходящаяся почти всюду последовательность случайных величин: [math]displaystyle{ X_nto X }[/math]. Пусть в дополнение существует интегрируемая случайная величина [math]displaystyle{ Y }[/math], такая что [math]displaystyle{ forall ninNquad|X_n|leqslant Y }[/math] почти наверное. Тогда случайные величины [math]displaystyle{ X_n,;X }[/math] интегрируемы и
- [math]displaystyle{ limlimits_{ntoinfty}mathbb{E}(X_n)=mathbb{E}(X) }[/math] .
- Тождество Вальда: для независимых одинаково распределённых случайных величин [math]displaystyle{ X_1,…,X_N }[/math], где [math]displaystyle{ N }[/math] является положительной целочисленной случайной величиной, независимой от [math]displaystyle{ X_i }[/math], при условии, что [math]displaystyle{ X_i }[/math] и [math]displaystyle{ N }[/math] имеют конечное математическое ожидание, будет выполняться следующее равенство:
-
- [math]displaystyle{ mathbb{E}left(sum_{i=1}^{N}X_iright)=mathbb{E}(N)mathbb{E}(X) }[/math]
- Математическое ожидание случайной величины [math]displaystyle{ X }[/math] равно значению первой производной её производящей функции моментов [math]displaystyle{ G(u) }[/math] в точке 0:
- [math]displaystyle{ mathbb{E}(X) = G'(0) }[/math].
Примеры
- Пусть случайная величина имеет дискретное равномерное распределение, то есть [math]displaystyle{ mathbb{P}(X = x_i) = frac{1}{n},; i=1,ldots, n. }[/math] Тогда её математическое ожидание
- [math]displaystyle{ mathbb{E}[X] = frac{1}{n} sumlimits_{i=1}^n x_i }[/math]
равно среднему арифметическому всех принимаемых значений.
- Пусть случайная величина имеет непрерывное равномерное распределение на интервале [math]displaystyle{ [a,b] }[/math], где [math]displaystyle{ alt b }[/math]. Тогда её плотность имеет вид [math]displaystyle{ f_X(x) = frac{1}{b-a} mathbf{1}_{[a,b]}(x) }[/math] и математическое ожидание равно
- [math]displaystyle{ mathbb{E}[X] = intlimits_{a}^b!frac{x}{b-a}, dx = frac{a+b}{2} }[/math].
- Пусть случайная величина [math]displaystyle{ X }[/math] имеет стандартное распределение Коши. Тогда
- [math]displaystyle{ intlimits_{-infty}^{infty}!xf_X(x), dx = infty }[/math],
то есть математическое ожидание [math]displaystyle{ X }[/math] не определено.
См. также
- Дисперсия случайной величины
- Моменты случайной величины
- Условное математическое ожидание
Примечания
- ↑ «Математическая энциклопедия» / Главный редактор И. М. Виноградов. — : «Советская энциклопедия», 1979. — 1104 с. — (51[03] М34). — 148 800 экз.
- ↑ А. Н. Ширяев. 1 // «Вероятность». — : МЦНМО, 2007. — 968 с. — ISBN 978-5-94057-036-3, 978-5-94057-106-3, 978-5-94057-105-6.
- ↑ В.Е.Гмурман. Часть вторая. Случайные величины. ->
Глава 4. Дискретные случайные величины. ->
Параграф 3. // [http://elenagavrile.narod.ru/ms/gmurman.pdf РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ И
МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ]. — 1979. — С. 63. — 400 с. Архивная копия от 21 января 2022 на Wayback Machine - ↑ Пытьев Ю. П., Шишмарев И. А., Теория вероятностей, математическая статистика и элементы теории возможностей для физиков. — М.: Физический факультет МГУ, 2010.
- ↑ Теория вероятностей: 10.2. Теоремы о числовых характеристиках. sernam.ru. Дата обращения: 10 января 2018. Архивировано 10 января 2018 года.
Литература
- Феллер В. Глава XI. Целочисленные величины. Производящие функции // Введение в теорию вероятностей и её приложения = An introduction to probability theory and its applicatons, Volume I second edition / Перевод с англ. Р. Л. Добрушина, А. А. Юшкевича, С. А. Молчанова Под ред. Е. Б. Дынкина с предисловием А. Н. Колмогорова. — 2-е изд. — М.: Мир, 1964. — С. 270—272.