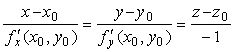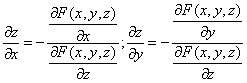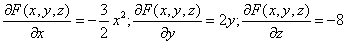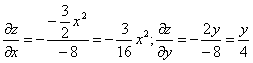Вектор нормали поверхности как найти

Касательная плоскость и нормаль к поверхности

Касательной плоскостью к поверхности σ в её точке М₀ называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М₀.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M₀(x₀,y₀,z₀) имеет вид:

Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M₀(0;1).
Решение. Запишем уравнения касательной в общем виде: z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 0 , y₀ = 1 , тогда z₀ = 5
Найдем частные производные функции z = x^3+5*y :
f’_x(x,y) = (x 3 +5•y)’_x = 3•x 2
f’_x(x,y) = (x 3 +5•y)’_y = 5
В точке М₀(0,1) значения частных производных:
f’_x(0;1) = 0
f’_y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 5 = 0(x — 0) + 5(y — 1) или -5•y+z = 0

Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M₀(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:

Для нашей функции:

Тогда:

В точке М₀(1,0,1) значения частных производных:
f’_x(1;0;1) = -3 /₁₆
f’_y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 1 = -3 /₁₆(x — 1) + 0(y — 0) или 3 /₁₆•x+z- 19 /₁₆ = 0

Пример . Поверхность σ задана уравнением z= y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М₀(x₀, y₀, z₀), принадлежащей ей, если x₀ = –1, y₀ = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x 3 :
f_x’(x, y) = (y/x + xy – 5x 3 )’_x = – y/x 2 + y – 15x 2 ;
f_y’ (x, y) = (y/x + xy – 5x 3 )’_y = 1/x + x.
Точка М₀(x₀, y₀, z₀) принадлежит поверхности σ, поэтому можно вычислить z₀, подставив заданные x₀ = –1 и y₀ = 2 в уравнение поверхности:

Пример №1 . Дана функция z=f(x,y) и две точки А(х₀, y₀) и В(х₁,y₁). Требуется: 1) вычислить значение z₁ функции в точке В; 2) вычислить приближенное значение z₁ функции в точке В исходя из значения z₀ функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x₀,y₀,z₀).
Решение.
Запишем уравнения касательной в общем виде:
z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 1, y₀ = 2, тогда z₀ = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_x = 2•x+3•y 3
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_y = 9•x•y 2
В точке М₀(1,2) значения частных производных:
f’_x(1;2) = 26
f’_y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26•x-36•y+z+73 = 0

Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).
Скачать решение

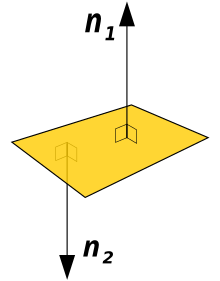
Нормальный вектор плоскости, координаты нормального вектора плоскости

Существует ряд заданий, которым для решения необходимо нормальный вектор на плоскости, чем саму плоскость. Поэтому в этой статье получим ответ на вопрос определения нормального вектора с примерами и наглядными рисунками. Определим векторы трехмерного пространства и плоскости по уравнениям.

Нормальный вектор плоскости – определение, примеры, иллюстрации

Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.

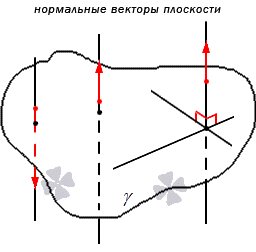
Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.

Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.

Нормальные векторы располагаются на параллельных прямых, поэтому они все коллинеарны. То есть, при нормальном векторе n → , расположенном в плоскости γ , вектор t · n → , имея ненулевое значение параметра t , также нормальный вектор плоскости γ . Любой вектор может быть рассмотрен как направляющий вектор прямой, которая перпендикулярна этой плоскости.

Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.

Рассмотрим на примере нормального вектора на плоскости.

Задана прямоугольная система координат О х у z в трехмерном пространстве. Координатные векторы i → , j → , k → считаются нормальными векторами плоскостей O y z , O x z и O x y . Это суждение верно, так как i → , j → , k → ненулевые и расположены на координатных прямых O x , O y и O z . Эти прямые перпендикулярны координатным плоскостям O y z , O x z и O x y .

Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости

Статья предназначена для того, чтобы научить находить координаты нормального вектора плоскости при известном уравнении плоскости прямоугольной системы координат О х у z . Для определения нормального вектора n → = ( A , B , C ) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид A x + B y + C z + D = 0 . То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.

Найти координаты нормального вектора, принадлежащего плоскости 2 x — 3 y + 7 z — 11 = 0 .

По условию имеем уравнение плоскости. Необходимо обратить внимание на коэффициенты, так как они и являются координатами нормального вектора заданной плоскости. Отсюда получаем, что n → = ( 2 , — 3 , 7 ) — это нормальный вектор плоскости. Все векторы плоскости задаются при помощи формулы t · n → = 2 · t , — 3 · t , 7 · t , t является любым действительным числом не равным нулю.

Ответ: n → = ( 2 , — 3 , 7 ) .

Определить координаты направляющих векторов заданной плоскости x + 2 z — 7 = 0 .

По условию имеем, что дано неполное уравнение плоскости. Чтобы увидеть координаты, необходимо преобразовать уравнение x + 2 z — 7 = 0 к виду 1 · x + 0 · y + 2 z — 7 = 0 . Отсюда получим, что координаты нормального вектора данной плоскости равны ( 1 , 0 , 2 ) . Тогда множество векторов будет иметь такую форму записи ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

Ответ: ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

При помощи уравнения плоскости в отрезках, имеющего вид x a + y b + z c = 1 , и общего уравнения плоскости возможна запись нормального вектора этой плоскости, где координаты равны 1 a , 1 b , 1 c .

Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Поверхности. Касательная плоскость и нормаль

Краткие теоретические сведения

Способы задания поверхностей

Рассматриваем вектор–функцию двух скалярных аргументов: $$vec=vec(u,v).$$ Годографом такой функции является поверхность.

Запишем четыре способа задания поверхности: 1. Векторное уравнение: $$vec=vec(u,v).$$ 2. Параметрическое уравнение: $$x=x(u,v),,, y=y(u,v),,, z=z(u,v).$$ 3. Неявное уравнение: $$varPhi(x,y,z)=0.$$ 4. Явное уравнение: $$z=z(x,y).$$

Поверхность называется регулярной ($k$ раз дифференцируемой), если у каждой точки этой поверхности есть окрестность, допускающая регулярную параметризацию (то есть функции $x(u,v), y(u,v),z=z(u,v)$ $k$ раз непрерывно дифференцируемы). При $k=1$ поверхность называется гладкой.

Регулярная поверхность в окрестности каждой своей точки допускает бесчисленное множество параметризаций.

Кривая, лежащая на поверхности $vec=vec(u,v)$, задается уравнениями $$ u=u(t),,, v=v(t).$$ Линии $u=mbox$, $v=mbox$ являются координатными линиями данной параметризации поверхности.

Решение задач

Задача 1 (Феденко №544)

Дана поверхность begin x=u+v, ,, y=u-v,,, z=uv. end Проверить, принадлежат ли ей точки $A(4,2,3)$ и $B(1,4,-2)$.

Ответ. Точка $A$ принадлежит, так как ее координаты удовлетворяют системе уравнений, задающих поверхность. Точка $B$ не принадлежит поверхности.

Задача 2 (Феденко № 546)

Найдите неявное уравнение поверхности, заданной параметрическими уравнениями: begin begin x & = x_0 + a,mbox,u,mbox,v, \ y & = y_0 + b,mbox,u,mbox,v, \ z & = z_0 + c,mbox,u. end end

Ответ. Эллипсоид с полуосями $a$, $b$, $c$ и центром в точке $(x_0, y_0, z_0)$: begin frac<(x-x_0)^2>+frac<(y-y_0)^2>+frac<(z-z_0)^2>=1. end

Задача 3 (Феденко №528)

В плоскости $xOz$ задана кривая $x=f(u)$, $z=g(u)$, не пересекающая ось $Oz$. Найдите параметризацию поверхности, полученной при вращении этой кривой вокруг оси $Oz$.

Решение задачи 3

Произвольная точка $M$, принадлежащая кривой и имеющая координаты $x_0=f(u_0)$, $y_0=0$, $z_0=g(u_0)$, движется по окружности с центром на оси $Oz$ и радиусом $R=f(u_0)$ в плоскости, параллельной плоскости $xOy$: $z=g(u_0)$. Поэтому изменение ее координат можно записать следующими уравнениями: begin left< begin x_0 & = & f(u_0),mbox,v, \ y_0 & = & f(u_0),mbox,v, \ z_0 & = & g(u_0). \ end right. end

Поскольку точка $M$ произвольная, уравнение искомой поверхности: begin left< begin x & = & f(u),mbox,v, \ y & = & f(u),mbox,v, \ z & = & g(u). \ end right. end

Касательная плоскость. Нормаль

Краткие теоретические сведения

Пусть $vec=vec(u,v)in C^1$ — поверхность, проходящая через точку $P(u_0, v_0)$. Пусть $u=u(t)$, $v=v(t)$ — уравнения гладкой кривой, проходящей через точку $P(u_0, v_0)$ и лежащей на заданной поверхности.

Пусть точка $P$ не является особой, то есть ранг матрицы begin left( begin x_u & y_u & z_u \ x_v & y_v & z_v \ end right) end в точке $P$ равен $2$ (для особой точки ранг меньше $2$). Если поверхность задана неявно $varPhi(x,y,z)=0$, то в не особой точке $P$ выполняется условие: $varPhi_x^2+varPhi_y^2+varPhi_z^2neq0.$

Касательная к кривой $u=u(t)$, $v=v(t)$ на поверхности $vec=vec(u,v)$ определяется вектором: begin displaystylefrac>

=vec_udisplaystylefrac

+vec_vdisplaystylefrac

, end где $vec_u=displaystylefrac>$, $vec_v=displaystylefrac>$. Для разных кривых, проходящих через точку $P(u_0, v_0)$, значения $displaystylefrac

$, $displaystylefrac

$ будут разными, а $vec_u$, $vec_v$ теми же. Следовательно, все векторы $displaystylefrac>

$ лежат в одной плоскости, определяемой векторами $vec_u$, $vec_v$. Эта плоскость называется касательной плоскостью к поверхности в точке $P$. Запишем уравнение касательной плоскости.

Обозначения:
— $vec=$ — радиус-вектор произвольной точки касательной плоскости.
— $vec=$ — радиус вектор точки $P(u_0, v_0)$.
— Частные производные $x_u$, $y_u$, $z_u$, $x_v$, $y_v$, $z_v$ вычисляются в точке $P(u_0, v_0)$.

Уравнение касательной плоскости:

1. Если поверхность задана векторно, то уравнение касательной плоскости можно записать через смешанное произведение трех линейно зависимых векторов: $$ left(vec-vec, , vec_u, , vec_v right)=0. $$ 2. Если поверхность задана параметрически, запишем определитель: begin left| begin X-x & Y-y & Z-z \ x_u & y_u & z_u\ x_v & y_v & z_v\ end right|=0 end 3. Если поверхность задана неявным уравнением: begin varPhi_x(X-x)+varPhi_y(Y-y)+varPhi_z(Z-z)=0. end 4. В случая явного задания поверхности, уравнение касательной плоскости примет вид: begin (Z-z)=z_x(X-x)+z_y(Y-y). end

Нормалью поверхности в точке $P$ называется прямая, проходящая через $P$ перпендикулярно касательной плоскости в этой точке.

Уравнение нормали:

1.$$ vec=vec + lambdavec, ,, vec=vec_utimesvec_v. $$ 2. begin displaystylefrac< left| begin y_u & z_u\ y_v & z_v\ end right|>= displaystylefrac< left| begin z_u & x_u\ z_v & x_v\ end right|>= displaystylefrac< left| begin x_u & y_u\ x_v & y_v\ end right|>. end 3. begin displaystylefrac<varPhi_x>=displaystylefrac<varPhi_y>=displaystylefrac<varPhi_z>. end 4. begin displaystylefrac=displaystylefrac=displaystylefrac<-1>. end

Решение задач

Задача 1 (Феденко №574)

Дана поверхность begin x=u,mbox,v,,, y=u,mbox,v,,, z=u. end Написать:
а) уравнение касательной плоскости к поверхности;
б] уравнение нормали к поверхности;
в) касательной к линии $u=2$
в точке $Mleft(u=2, v=displaystylefrac<pi><4>right)$ поверхности.

Задача 2

Через точки $A(0,1,0)$ и $B(1,0,0)$ провести плоскость, касательную к поверхности $vec=$.

Ответ. $z=0, -2X-2Y+Z+2=0$.

Задача 3

Построить касательную плоскость к поверхности $y=x^2+z^2$, перпендикулярную вектору $vec<2,1,-1>$.

Задача 4

Через точку $M(1,2,1)$ провести плоскость, касательную к поверхности $x^2+y^2-z^2=0$.

Ответ. $X-Z=0$, $3X-4Y+5Z=0$.

Задача 5 (Феденко №594)

Докажите, что поверхности begin z=mbox(xy), ,, x^2-y^2=a end ортогональны в точках их пересечения.

Решение задачи 5

Запишем направляющие векторы нормалей к поверхностям, проведенным в точках их пересечения: begin begin vec_1&=left<frac<mbox^2(x_0y_0)>,frac<mbox^2(x_0y_0)>,-1right>,\ vec_2&=left<2x_0,-2y_0,0right>. end end Скалярные произведения векторов $n_1$ и $n_2$ равны нулю, следовательно векторы ортогональны. begin n_1cdot n_2=0. end

источники:

http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/normalnyj-vektor-ploskosti-koordinaty-normalnogo-v/

http://vmath.ru/vf5/diffgeom/seminar5

Пусть имеем поверхность, заданную уравнением вида

Введем следующее определение.

Определение 1. Прямая линия называется касательной к поверхности в некоторой точке , если она является

касательной к какой-либо кривой, лежащей на поверхности и проходящей через точку .

Так как через точку Р проходит бесконечное число различных кривых, лежащих на поверхности, то и касательных к поверхности, проходящих через эту точку, будет, вообще говоря, бесконечное множество.

Введем понятие об особых и обыкновенных точках поверхности

Если в точке все три производные равны нулю или хотя бы одна из этих производных не существует, то точка М называется особой точкой поверхности. Если в точке все три производные существуют и непрерывны, причем хотя бы одна из них отлична от нуля, то точка М называется обыкновенной точкой поверхности.

Теперь мы можем сформулировать следующую теорему.

Теорема. Все касательные прямые к данной поверхности (1) в ее обыкновенной точке Р лежат в одной плоскости.

Доказательство. Рассмотрим на поверхности некоторую линию L (рис. 206), проходящую через данную точку Р поверхности. Пусть рассматриваемая кривая задана параметрическими уравнениями

Касательная к кривой будет касательной к поверхности. Уравнения этой касательной имеют вид

Если выражения (2) подставить в уравнение (1), то это уравнение превратится в тождество относительно t, так как кривая (2) лежит на поверхности (1). Дифференцируя его по получим

Проекции этого вектора зависят от — координат точки Р; заметим, что так как точка Р обыкновенная, то эти проекции в точке Р одновременно не обращаются в нуль и потому

касательный к кривой, проходящей через точку Р и лежащей на поверхности. Проекции этого вектора вычисляются на основании уравнений (2) при значении параметра t, соответствующем точке Р.

Вычислим скалярное произведение векторов N и которое равно сумме произведений одноименных проекций:

На основании равенства (3) выражение, стоящее в правой части, равно нулю, следовательно,

Из последнего равенства следует, что вектор ЛГ и касательный вектор к кривой (2) в точке Р перпендикулярны. Проведенное рассуждение справедливо для любой кривой (2), проходящей через точку Р и лежащей на поверхности. Следовательно, каждая касательная к поверхности в точке Р перпендикулярна к одному и тому же вектору N и потому все эти касательные лежат в одной плоскости, перпендикулярной к вектору ЛГ. Теорема доказана.

Определение 2. Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную ее точку Р, называется касательной плоскостью к поверхности в точке Р (рис. 207).

Заметим, что в особых точках поверхности может не существовать касательной плоскости. В таких точках касательные прямые к поверхности могут не лежать в одной плоскости. Так, например, вершина конической поверхности является особой точкой.

Касательные к конической поверхности в этой точке не лежат в одной плоскости (они сами образуют коническую поверхность).

Напишем уравнение касательной плоскости к поверхности (1) в обыкновенной точке. Так как эта плоскость перпендикулярна вектору (4), то, следовательно, ее уравнение имеет вид

Если уравнение поверхности задано в форме или уравнение касательной плоскости в этом случае примет вид

Замечание. Если в формуле (6) положим , то эта формула примет вид

ее правая часть представляет собой полный дифференциал функции . Следовательно, . Таким образом, полный дифференциал функции двух переменных в точке соответствующий приращениям независимых переменных х и у, равен соответствующему приращению аппликаты касательной плоскости к поверхности, которая является графиком данной функции.

О пределение 3. Прямая, проведенная через точку поверхности (1) перпендикулярно к касательной плоскости, называется нормалью к поверхности (рис. 207).

Напишем уравнения нормали. Так как ее направление совпадает с направлением вектора N, то ее уравнения будут иметь вид

Скачать с Depositfiles

4. ТЕОРИЯ ПОВЕРХНОСТЕЙ.

4.1 УРАВНЕНИЯ ПОВЕРХНОСТЕЙ.

Поверхность в трёхмерном пространстве может быть задана:

1) неявно:
F

(
x

,

y

,

z

)

=0 (4.1)

2) явно:
z

=

f

(
x

,

y

)

(4.2)

3) параметрически: (4.3)

или:
(4.3’)

где скалярные аргументы
иногда называют криволинейными координатами. Например, сферу
удобно задавать в сферических координатах:
.

4.2 КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К ПОВЕРХНОСТИ.

Если линия лежит на поверхности (4.1), то координаты её точек удовлетворяют уравнению поверхности:

Дифференцируя это тождество, получим:

(4.4)

или
(4.4
’
)

в каждой точке кривой на поверхности. Таким образом, вектор градиента в неособых точках поверхности (в которых функция (4.5) дифференцируема и
) перпендикулярен касательным векторам к любым линиям на поверхности, т.е может быть использован в качестве вектора нормали для составления уравнения касательной плоскости в точке М
0
(x

0

,

y

0

,

z

0

) поверхности

(4.6)

и в качестве направляющего вектора в уравнении нормали:

(4.7)

В случае явного (4.2) задания поверхности уравнения касательной плоскости и нормали соответственно примут вид:

(4.8)

и
(4.9)

При параметрическом представлении поверхности (4.3) векторы
лежат в касательной плоскости и уравнение касательной плоскости может быть записано в виде:

(4.10)

а в качестве направляющего вектора нормали может быть принято их векторное произведение:

и уравнение нормали может быть записано в виде:

(4.11)

где
— значения параметров соответствующие точке М
0
.

В дальнейшем мы ограничимся рассмотрением лишь таких точек поверхности, где векторы

не равны нулю и не параллельны.

Пример 4.1
Составить уравнения касательной плоскости и нормали в точке М
0
(1,1,2) к поверхности параболоида вращения
.

Решение: Так как уравнение параболоида задано в явном виде, то согласно (4.8) и (4.9) нужно найти
в точке М
0
:

, а в точке М
0

. Тогда уравнение касательной плоскости в точке М
0
примет вид:

2(x

-1)+2(y

-1)-(z

-2)=0 или 2
x

+2
y



–
z
‑ 2=0, а уравнение нормали
.

Пример 4.2
Составить уравнения касательной плоскости и нормали в произвольной точке геликоида
, .

Решение. Здесь ,

Уравнение касательной плоскости:

или

Уравнения нормали:

.

4.3 ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ.

Если поверхность задается уравнением

то кривая
на ней может быть задана уравнением
(4.12)

Дифференциал радиус-вектора
вдоль кривой, отвечающий смещению из точки М
0
в близлежащую точку М, равен

(4.13)

Так как
— дифференциал дуги кривой, отвечающий тому же смещению), то

(4.14)

где .

Выражение в правой части (4.14) называется первой квадратичной формой поверхности и играет в теории поверхностей огромную роль.

Интегрирую дифференциал
ds

в пределах от
t

0
(соответствует точке М
0
) до
t
(соответствует точке М), получим длину соответствующего отрезка кривой

(4.15)

Зная первую квадратичную форму поверхности, можно находить не только длины, но и углы между кривыми.

Если
du

,

dv

— дифференциалы криволинейных координат, отвечающие бесконечно малому смещению по одной кривой, а
— по другой, то с учетом (4.13):

(4.16)

С помощью формулы

(4.17)

первая квадратичная форма дает возможность вычислить площадь области
поверхности.

Пример 4.3
На геликоиде , найти длину винтовой линии
между двумя точками .

Решение. Поскольку на винтовой линии
, то . Найдём в точке
первую квадратичную форму. Обозначив и
v

=

t

,

получим уравнение данной винтовой линии в виде . Квадратичная форма:

= ‑ первая квадратичная форма.

Здесь . В формуле (4.15) в данном случае
и длина дуги:

=

4.4 ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ.

Обозначим
‑ единичный вектор нормали к поверхности
:

(4.18)
.
(4.23)

Линия на поверхности называется линией кривизны, если ее направление в каждой точке является главным направлением.

4.6 ПОНЯТИЕ О ГЕОДЕЗИЧЕСКИХ ЛИНИЯХ НА ПОВЕРХНОСТИ.

Определение 4.1
. Кривая на поверхности называется геодезической, если ее главная нормаль в каждой точке, где кривизна отлична от нуля, совпадает с нормалью к поверхности.

Через каждую точку поверхности в любом направлении проходит, и при том только одна геодезическая. На сфере, например, геодезическими являются большие круги.

Параметризация поверхности называется полугеодезической, если одно семейство координатных линий состоит из геодезических, а второе ему ортогонально. Например, на сфере меридианы (геодезические) и параллели.

Геодезическая на достаточно малом отрезке является кратчайшей среди всех близких к ней кривых, соединяющих те же точки.

Уравнение нормальной плоскости

1.

4.

Касательная плоскость и нормаль к поверхности

Пусть дана некоторая поверхность, A — фиксированная точка поверхности и B — переменная точка поверхности,

(рис. 1).

Ненулевой вектор

называется нормальным вектором
к поверхности в точке A , если

Точка поверхности F (x , y , z) = 0 называется обыкновенной
, если в этой точке

1. частные производные F » x
   , F » y
   , F » z
   непрерывны;
2. (F » x
   )2
   + (F » y
   )2
   + (F » z
   )2
   ≠ 0 .

При нарушении хотя бы одного из этих условий точка поверхности называется особой точкой поверхности
.

Теорема 1.
Если M (x 0
, y 0
, z 0
) — обыкновенная точка поверхности F (x , y , z) = 0 , то вектор

= grad F (x 0 , y 0 , z 0 ) = F » x (x 0 , y 0 , z 0 ) + F » y (x 0 , y 0 , z 0 ) + F » z (x 0 , y 0 , z 0 )

(1)

является нормальным к этой поверхности в точке M (x 0
, y 0
, z 0
) .

Доказательство
приведено
в книге И.М. Петрушко, Л.А. Кузнецова, В.И. Прохоренко, В.Ф. Сафонова
«Курс высшей математики: Интегральное исчисление. Функции нескольких
переменных. Дифференциальные уравнения. М.: Изд-во МЭИ, 2002
(стр. 128).

Нормалью к поверхности
в
некоторой ее точке называется прямая, направляющий вектор которой
является нормальным к поверхности в этой точке и которая проходит через
эту точку.

Канонические уравнения нормали
можно представить в виде

x − x 0 F » x (x 0 , y 0 , z 0 ) = y − y 0 F » y (x 0 , y 0 , z 0 ) = z − z 0 F » z (x 0 , y 0 , z 0 ) .

(2)

Касательной плоскостью
к
поверхности в некоторой точке называется плоскость, которая проходит
через эту точку перпендикулярно нормали к поверхности в этой точке.

Из этого определения следует, что уравнение касательной плоскости
имеет вид:

(3)

Если точка поверхности является особой, то в этой точке нормальный к
поверхности вектор может не существовать, и, следовательно, поверхность
может не иметь нормали и касательной плоскости.

Геометрический смысл полного дифференциала функции двух переменных

Пусть функция z = f (x , y) дифференцируема в точке a (x 0
, y 0
) . Ее графиком является поверхность

f (x , y) − z = 0.

Положим z 0
= f (x 0
, y 0
) . Тогда точка A (x 0
, y 0
, z 0
) принадлежит поверхности.

Частные производные функции F (x , y , z) = f (x , y) − z суть

F » x
= f » x
, F » y
= f » y
, F » z
= − 1

и в точке A (x 0
, y 0
, z 0
)

1. они непрерывны;
2. F «2
   x
   + F «2
   y
   + F «2
   z
   = f «2
   x
   + f «2
   y
   + 1 ≠ 0 .

Следовательно, A — обыкновенная точка поверхности F (x , y , z) и в этой точке существует касательная плоскость к поверхности. Согласно (3), уравнение касательной плоскости имеет вид:

f » x
(x 0
, y 0
) (x − x 0
) + f » y
(x 0
, y 0
) (y − y 0
) − (z − z 0
) = 0.

Вертикальное смещение точки на касательной плоскости при переходе из точки a (x 0
, y 0
) в произвольную точку p (x , y) есть B Q (рис. 2). Соответствующее приращение аппликаты есть

(z − z 0
) = f » x
(x 0
, y 0
) (x − x 0
) + f » y
(x 0
, y 0
) (y − y 0
)

Здесь в правой части стоит дифференциалd
z функции z = f (x , y) в точке a (x 0
, x 0
). Следовательно,
d
f (x 0
, y 0
). есть приращение аппликаты точки плоскости касательной к графику функции f (x , y) в точке (x 0
, y 0
, z 0
= f (x 0
, y 0
)).

Из определения дифференциала следует, что расстояние между точкой P на графике функции и точкой Q на касательной плоскости есть бесконечно малая более высокого порядка, чем расстояние от точки p до точки a .

Рассмотрим геометрические приложения производной функции нескольких переменных. Пусть функция двух переменных задана неявно: . Эта функция в области своего определения изображается некоторой поверхностью (п. 5.1). Возьмем на данной поверхности произвольную точку , в которой все три частных производных , , существуют и непрерывны, причем хотя бы одна из них не равна нулю.

Точка с такими характеристиками называется обыкновенной

точкой поверхности. Если хотя бы одно из указанных выше требований не выполняется, то точка называется особой

точкой поверхности.

Через выбранную на поверхности точку можно провести множество кривых, к каждой из которых может быть проведена касательная.

Определение 5.8.1

. Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через некоторую точку , называется касательной плоскостью к данной поверхности в точке
.

Чтобы провести данную плоскость достаточно иметь две касательных прямых, то есть две кривых на поверхности. Это могут быть кривые, полученные в результате сечения данной поверхности плоскостями , (рис. 5.8.1).

Запишем уравнение касательной линии к кривой, лежащей на пересечении поверхности и плоскости . Поскольку данная кривая лежит в системе координат , то уравнение касательной к ней в точке , в соответствии с п. 2.7, имеет вид:

. (5.8.1)

Соответственно, уравнение касательной к кривой, лежащей на пересечении поверхности и плоскости , в системе координат в той же точке имеет вид:

. (5.8.2)

Воспользуемся выражением для производной неявно заданной функции (п. 5.7). Тогда , а . Подставляя эти производные в (5.8.1) и (5.8.2), получим, соответственно:

; (5.8.3)

. (5.8.4)

Поскольку полученные выражения не что иное, как уравнения прямых в канонической форме (п. 15), то из (5.8.3) получаем направляющий вектор , а из (5.8.4) – . Векторное произведение даст вектор, нормальный к данным касательным линиям, а, следовательно, и к касательной плоскости:

Отсюда следует, что уравнение касательной плоскости к поверхности в точке имеет вид (п. 14):

Определение 5.8.2

. Прямая, проведенная через точку поверхности перпендикулярно касательной плоскости в этой точке, называется нормалью к поверхности
.

Так как направляющий вектор нормали к поверхности совпадает с нормалью к касательной плоскости , то уравнение нормали имеет вид:

.

Скалярное поле

Пусть в пространстве задана область , занимающая часть или все это пространство. Пусть каждой точке этой области по какому-то закону поставлена в соответствие некоторая скалярная величина (число).

Определение 5.9.1

. Область в пространстве, каждой точке которой ставится в соответствие по известному закону некоторая скалярная величина , называется скалярным полем
.

Если с областью связана какая-то система координат, например, прямоугольная декартовая, то каждая точка приобретает свои координаты. В этом случае скалярная величина становится функцией координат: на плоскости – , в трехмерном пространстве – . Скалярным полем часто называют и саму функцию , описывающую данное поле. В зависимости от размерности пространства, скалярное поле может быть плоским, трехмерным и т.д.

Необходимо подчеркнуть, что величина скалярного поля зависит лишь от положения точки в области , но не зависит от выбора системы координат.

Определение 5.9.2

. Скалярное поле, зависящее только от положения точки в области , но не зависящее от времени, называется стационарным
.

Нестационарные скалярные поля, то есть зависящие от времени, в данном разделе нами рассматриваться не будут.

В качестве примеров скалярных полей можно назвать поле температур, поле давлений в атмосфере, поле высот над уровнем океана.

Геометрически скалярные поля часто изображаются с помощью так называемых линий или поверхностей уровня.

Определение 5.9.3

. Множество всех точек пространства, в которых скалярное поле имеет одно и то же значение называется поверхностью уровня или эквипотенциальной поверхностью. В плоском случае для скалярного поля это множество называется линией уровня или эквипотенциальной линией
.

Очевидно, что уравнение поверхности уровня имеет вид , линии уровня – . Придавая в данных уравнениях константе разные значения, получаем семейство поверхностей или линий уровня. Например, (вложенные друг в друга сферы с разными радиусами) или (семейство эллипсов).

В качестве примеров линий уровня из физики можно привести изотермы (линии равных температур), изобары (линии равных давлений); из геодезии – линии равных высот и т.д.

Графиком функции 2-х переменных z = f(x,y) является поверхность, проектирующаяся на плоскость XOY в область определения функции D.

Рассмотрим поверхность σ
, заданную уравнением z = f(x,y) , где f(x,y) – дифференцируемая функция, и пусть M 0 (x 0 ,y 0 ,z 0) – фиксированная точка на поверхности σ , т.е. z 0 = f(x 0 ,y 0).
Назначение
. Онлайн-калькулятор предназначен для нахождения уравнения касательной плоскости и нормали к поверхности
. Решение оформляется в формате Word
. Если необходимо найти уравнение касательной к кривой (y = f(x)), то необходимо использовать данный сервис .

Правила ввода функций
:

Правила ввода функций
:

Касательной плоскостью к поверхности
σ
в её точке М
0 называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ
через точку М
0 .

Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M 0 (x 0 ,y 0 ,z 0) имеет вид:

z – z 0 = f’ x (x 0 ,y 0)(x – x 0) + f’ y (x 0 ,y 0)(y – y 0)

Вектор называется вектором нормали к поверхности σ
в точке М 0 . Вектор нормали перпендикулярен касательной плоскости.

Нормалью к поверхности
σ
в точке М
0 называется прямая, проходящая через эту точку и имеющая направление вектора N.

Канонические уравнения нормали к поверхности, заданной уравнением z = f(x,y) , в точке M 0 (x 0 ,y 0 ,z 0), где z 0 = f(x 0 ,y 0), имеют вид:

Пример №1
. Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M 0 (0;1).

Решение
. Запишем уравнения касательной в общем виде: z — z 0 = f» x (x 0 ,y 0 ,z 0)(x — x 0) + f» y (x 0 ,y 0 ,z 0)(y — y 0)

По условию задачи x 0 = 0 , y 0 = 1 , тогда z 0 = 5

Найдем частные производные функции z = x^3+5*y:

f» x (x,y) = (x 3 +5 y)» x = 3 x 2

f» x (x,y) = (x 3 +5 y)» y = 5

В точке М 0 (0,1) значения частных производных:

f» x (0;1) = 0

f» y (0;1) = 5

Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М 0: z — 5 = 0(x — 0) + 5(y — 1) или -5 y+z = 0

Пример
. Поверхность σ
задана уравнением z
= y/x + xy
– 5x
3 . Найти уравнение касательной плоскости и нормали к поверхности σ
в точке М
0 (x
0 , y
0 , z
0), принадлежащей ей, если x
0 = –1, y
0 = 2.

Найдем частные производные функции z
= f
(x
, y
) = y/x + xy
– 5x
3:

f x ’(x
, y
) = (y/x + xy
– 5x
3)’ x = – y/x 2 + y
– 15x
2 ;

f y ’ (x
, y
) = (y/x + xy
– 5x
3)’ y = 1/x + x
.

Точка М
0 (x
0 , y
0 , z
0) принадлежит поверхности σ
, поэтому можно вычислить z
0 , подставив заданные x
0 = –1 и y
0 = 2 в уравнение поверхности:

z
= y/x + xy
– 5x
3

z
0 = 2/(-1) + (–1) 2 – 5 (–1) 3 = 1.

В точке М
0 (–1, 2, 1) значения частных производных:

f x ’(М
0) = –1/(-1) 2 + 2 – 15(–1) 2 = –15; f y ’(М
0) = 1/(-1) – 1 = –2.

Пользуясь формулой (5) получаем уравнение касательной плоскости к поверхности σ
в точке М
0:

z
– 1= –15(x
+ 1) – 2(y
– 2) z
– 1= –15x
– 15 – 2y +
4 15x
+ 2y
+ z
+ 10 = 0.

Пользуясь формулой (6) получаем канонические уравнения нормали к поверхности σ
в точке М
0: .

Ответы: уравнение касательной плоскости: 15x
+ 2y
+ z
+ 10 = 0; уравнения нормали: .

Пример №1
. Дана функция z=f(x,y) и две точки А(х 0 , y 0) и В(х 1 ,y 1). Требуется: 1) вычислить значение z 1 функции в точке В; 2) вычислить приближенное значение z 1 функции в точке В исходя из значения z 0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x 0 ,y 0 ,z 0).

Решение.


Запишем уравнения касательной в общем виде:
z — z 0 = f» x (x 0 ,y 0 ,z 0)(x — x 0) + f» y (x 0 ,y 0 ,z 0)(y — y 0)
По условию задачи x 0 = 1, y 0 = 2, тогда z 0 = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f» x (x,y) = (x 2 +3 x y +y 2)» x = 2 x+3 y 3
f» x (x,y) = (x 2 +3 x y +y 2)» y = 9 x y 2
В точке М 0 (1,2) значения частных производных:
f» x (1;2) = 26
f» y (1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М 0:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26 x-36 y+z+73 = 0

Пример №2
. Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).

В самом общем случае нормаль к поверхности
представляет ее локальную кривизну, и,
следовательно, направление зеркального
отражения (рис. 3.5). Применительно к нашим
знаниям можно сказать, что нормалью
называется вектор, определяющий
ориентацию грани (рис. 3.6).

Рис. 3.5 Рис. 3.6

Во многих алгоритмах удаления невидимых
линий и поверхностей используются
только ребра и вершины, поэтому, для
того чтобы объединить их с моделью
освещения, необходимо знать приближенное
значение нормали на ребрах и в вершинах.
Пусть заданы уравнения плоскостей
полигональных граней, тогда нормаль к
их общей вершине равна среднему значению
нормалей ко всем многоугольникам,
сходящимся к этой вершине. Например, на
рис. 3.7 направление приближенной нормали
в точке V₁есть:

n_v1
= (a₀
+ a₁
+ a₄)i
+ (b₀
+ b₁
+ b₄)j
+ (c₀
+ c₁
+ c₄)k,
(3.15)

где a₀, a₁,
a₄, b₀, b₁,
b₄, c₀, c₁,
c₄— коэффициенты уравнений
плоскостей трех многоугольниковP₀,
P₁, P₄,окружающихV₁. Отметим, что
если требуется найти только направление
нормали, то делить результат на количество
граней необязательно.

Если же уравнения плоскостей не заданы,
то нормаль к вершине можно определить,
усредняя векторные произведения всех
ребер, пересекающихся в вершине. Еще
раз, рассматривая вершину V₁на
рис. 3.7, найдем направление приближенной
нормали:

n_v1
= V₁V₂

V₁V₄
+V₁V₅

V₁V₂
+ V₁V₄

V₁V₅
(3.16)

Рис. 3.7 — Аппроксимация
нормали к полигональной поверхности

Следует
обратить внимание на то, что необходимы
только внешние нормали. Кроме того, если
полученный вектор не нормируется, то
его величина зависит от количества и
площади конкретных многоугольников, а
также от количества и длины конкретных
ребер. Сильнее проявляется влияние
многоугольников с большей площадью и
более длинными ребрами.

Когда
нормаль к поверхности используется для
определения ин­тенсивности и для
изображения объекта или сцены выполняется
перспективное преобразование, то нормаль
следует вычислять до перспективного
деления. В противном случае направление
нор­мали будет искажено, а это приведет
к тому, что интенсивность, задаваемая
моделью освещения, будет определена
неправильно.

Если известно аналитическое описание
плоскости (поверхности), то нормаль
вычисляется непосредственно. Зная
уравнение плоскости каждой грани
многогранника, можно найти направление
внешней нормали.

Если
уравнение плоскости имеет вид:

, (3.17)

то вектор нормали к этой плоскости
записывается следующим образом:

, (3.18)

где
— единичные векторы осейx,y,zсоответственно.

Величина dвычисляется с помощью
произвольной точки, принадлежащей
плоскости, например, для точки ()

. (3.19)

Пример.Рассмотрим 4-х сторонний
плоский многоугольник, описываемый
4-мя вершинами V1(1,0,0), V2(0,1,0), V3(0,0,1) и
V4(1,1,1) (см. рис. 3.7).

Уравнение
плоскости имеет вид:

x
+ y
+ z
— 1 = 0.

Получим нормаль к этой плоскости,
используя векторное произведение пары
векторов, являющихся смежными ребрами
к одной из вершин, например, V1:

Во
многих алгоритмах удаления невидимых
линий и поверхностей используются
только ребра или вершины, поэтому, для
того, чтобы объединить их с моделью
освещения, необходимо знать приближенное
значение нормали на ребрах и в вершинах.

Пусть
заданы уравнения плоскостей граней
многогранника, тогда нормаль к их общей
вершине равна среднему значению нормалей
ко всем граням, сходящимся в этой вершине.

Например, на рис.3.7 направление приближенной
нормали в точке
есть

,

где
— коэффициенты уравнений плоскостей
3-х многоугольниковP0,P1иP4,
окружающих.

Если
же уравнение плоскостей не заданы, то
нормаль к вершине можно определить,
усредняя векторные произведения всех
ребер, пересекающихся в вершине. Опять,
выбирая вершину
(см.
рис. 3.7), найдем направление приближенной
нормали:

Замечания:

1. нам необходимы только внешние нормали;

2. вычисление нормали осуществляется до
   перспективных преобразований, в
   противном случае направление нормали
   будет искажено, что приведет к неправильной
   модели освещения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

From Wikipedia, the free encyclopedia

This article is about the normal to 3D surfaces. For the normal to 3D curves, see Frenet–Serret formulas.

In geometry, a normal is an object (e.g. a line, ray, or vector) that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the (infinite) line perpendicular to the tangent line to the curve at the point.
A normal vector may have length one (in which case it is a unit normal vector) or its length may represent the curvature of the object (a curvature vector); its algebraic sign may indicate sides (interior or exterior).

In three-dimensional space, a surface normal, or simply normal, to a surface at point P is a vector perpendicular to the tangent plane of the surface at P. The word normal is also used as an adjective: a line normal to a plane, the normal component of a force, the normal vector, etc. The concept of normality generalizes to orthogonality (right angles).

The concept has been generalized to differentiable manifolds of arbitrary dimension embedded in a Euclidean space. The normal vector space or normal space of a manifold at point is the set of vectors which are orthogonal to the tangent space at
Normal vectors are of special interest in the case of smooth curves and smooth surfaces.

The normal is often used in 3D computer graphics (notice the singular, as only one normal will be defined) to determine a surface’s orientation toward a light source for flat shading, or the orientation of each of the surface’s corners (vertices) to mimic a curved surface with Phong shading.

The foot of a normal at a point of interest Q (analogous to the foot of a perpendicular) can be defined at the point P on the surface where the normal vector contains Q.
The normal distance of a point Q to a curve or to a surface is the Euclidean distance between Q and its foot P.

Normal to surfaces in 3D space[edit]

Calculating a surface normal[edit]

For a convex polygon (such as a triangle), a surface normal can be calculated as the vector cross product of two (non-parallel) edges of the polygon.

For a plane given by the equation the vector is a normal.

For a plane whose equation is given in parametric form

where is a point on the plane and are non-parallel vectors pointing along the plane, a normal to the plane is a vector normal to both and which can be found as the cross product

If a (possibly non-flat) surface in 3D space is parameterized by a system of curvilinear coordinates with and real variables, then a normal to S is by definition a normal to a tangent plane, given by the cross product of the partial derivatives

If a surface is given implicitly as the set of points satisfying then a normal at a point on the surface is given by the gradient

since the gradient at any point is perpendicular to the level set

For a surface in given as the graph of a function an upward-pointing normal can be found either from the parametrization giving

or more simply from its implicit form giving
Since a surface does not have a tangent plane at a singular point, it has no well-defined normal at that point: for example, the vertex of a cone. In general, it is possible to define a normal almost everywhere for a surface that is Lipschitz continuous.

Choice of normal[edit]

The normal to a (hyper)surface is usually scaled to have unit length, but it does not have a unique direction, since its opposite is also a unit normal. For a surface which is the topological boundary of a set in three dimensions, one can distinguish between the inward-pointing normal and outer-pointing normal. For an oriented surface, the normal is usually determined by the right-hand rule or its analog in higher dimensions.

If the normal is constructed as the cross product of tangent vectors (as described in the text above), it is a pseudovector.

Transforming normals[edit]

in this section we only use the upper matrix, as translation is irrelevant to the calculation

When applying a transform to a surface it is often useful to derive normals for the resulting surface from the original normals.

Specifically, given a 3×3 transformation matrix we can determine the matrix that transforms a vector perpendicular to the tangent plane into a vector perpendicular to the transformed tangent plane by the following logic:

Write n′ as We must find

Choosing such that or will satisfy the above equation, giving a perpendicular to or an perpendicular to as required.

Therefore, one should use the inverse transpose of the linear transformation when transforming surface normals. The inverse transpose is equal to the original matrix if the matrix is orthonormal, that is, purely rotational with no scaling or shearing.

Hypersurfaces in n-dimensional space[edit]

For an -dimensional hyperplane in -dimensional space given by its parametric representation

where is a point on the hyperplane and for are linearly independent vectors pointing along the hyperplane, a normal to the hyperplane is any vector in the null space of the matrix meaning That is, any vector orthogonal to all in-plane vectors is by definition a surface normal. Alternatively, if the hyperplane is defined as the solution set of a single linear equation then the vector is a normal.

The definition of a normal to a surface in three-dimensional space can be extended to -dimensional hypersurfaces in A hypersurface may be locally defined implicitly as the set of points satisfying an equation where is a given scalar function. If is continuously differentiable then the hypersurface is a differentiable manifold in the neighbourhood of the points where the gradient is not zero. At these points a normal vector is given by the gradient:

The normal line is the one-dimensional subspace with basis

Varieties defined by implicit equations in n-dimensional space[edit]

A differential variety defined by implicit equations in the -dimensional space is the set of the common zeros of a finite set of differentiable functions in variables

The Jacobian matrix of the variety is the matrix whose -th row is the gradient of By the implicit function theorem, the variety is a manifold in the neighborhood of a point where the Jacobian matrix has rank At such a point the normal vector space is the vector space generated by the values at of the gradient vectors of the

In other words, a variety is defined as the intersection of hypersurfaces, and the normal vector space at a point is the vector space generated by the normal vectors of the hypersurfaces at the point.

The normal (affine) space at a point of the variety is the affine subspace passing through and generated by the normal vector space at

These definitions may be extended verbatim to the points where the variety is not a manifold.

Example[edit]

Let V be the variety defined in the 3-dimensional space by the equations

This variety is the union of the -axis and the -axis.

At a point where the rows of the Jacobian matrix are and Thus the normal affine space is the plane of equation Similarly, if the normal plane at is the plane of equation

At the point the rows of the Jacobian matrix are and Thus the normal vector space and the normal affine space have dimension 1 and the normal affine space is the -axis.

Uses[edit]

• Surface normals are useful in defining surface integrals of vector fields.
• Surface normals are commonly used in 3D computer graphics for lighting calculations (see Lambert’s cosine law), often adjusted by normal mapping.
• Render layers containing surface normal information may be used in digital compositing to change the apparent lighting of rendered elements.^{[citation needed]}
• In computer vision, the shapes of 3D objects are estimated from surface normals using photometric stereo.^[1]

Normal in geometric optics[edit]

The normal ray is the outward-pointing ray perpendicular to the surface of an optical medium at a given point.^[2] In reflection of light, the angle of incidence and the angle of reflection are respectively the angle between the normal and the incident ray (on the plane of incidence) and the angle between the normal and the reflected ray.

See also[edit]

• Dual space – In mathematics, vector space of linear forms
• Ellipsoid normal vector
• Normal bundle – term related to the preceding concept
• Pseudovector – Physical quantity that changes sign with improper rotation
• Vertex normal – directional vector associated with a vertex, intended as a replacement to the true geometric normal of the surface

References[edit]

External links[edit]

• Weisstein, Eric W. «Normal Vector». MathWorld.
• An explanation of normal vectors from Microsoft’s MSDN
• Clear pseudocode for calculating a surface normal from either a triangle or polygon.