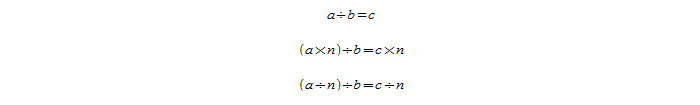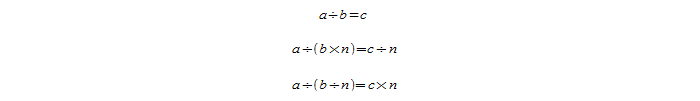Содержание:
- § 1 Деление на двузначное, трехзначное и т.д. числа
- § 2 Прикидка частного
- § 3 Краткие итоги урока
§ 1 Деление на двузначное, трехзначное и т.д. числа
В этом уроке поговорим о деление на двузначное, трехзначное, четырехзначное и т.д. число с однозначным частным.
Всем нам известно, что обратное действие для деления – это умножение. Другими словами, чтобы проверить правильность выполнения деления, необходимо частное умножить на делитель.
Рассмотрим следующую задачу:
какие из чисел 1, 2, 3, 4, 5, 6 являются частным чисел 432 и 72?
Чтобы ответить на поставленный вопрос, проверим каждое число путем умножения на делитель 72.
Проверяем число 1: 72 · 1 = 72, 72 < 432, значит, 1 не подходит.
Проверяем число 2: 72 · 2 = 144, 144 < 432, значит, 2 не подходит.
Проверяем число 3: 72 · 3 = 216, 216 < 432, значит, 3 не подходит.
Проверяем число 4: 72 · 4 = 288, 288 < 432, значит, 4 не подходит.
Проверяем число 5: 72 · 5 = 360, 360 < 432, значит, 5 не подходит.
Проверяем число 6: 72 · 6 = 432, значит, 6 подходит.
Таким образом, путем последовательного умножения чисел 1, 2, 3, 4, 5, 6 на делитель 72 мы подобрали частное чисел 432 и 72: 432 : 72 = 6. Но данный путь можно сократить. Если мы вначале выполним прикидку 432 : 72 ≈ 420 : 70 = 6, то увидим, что проверку можно было начать сразу с числа 6.
Исходя из этого, можно сделать вывод, что при делении на двузначное, трехзначное, четырехзначное и т.д. число необходимо выполнить прикидку частного, а затем путем умножения на делитель подобрать искомое частное, начиная с приближенного его значения.
Опираясь на данное правило, найдем частное чисел 1028 и 257
1.Выполняем прикидку частного: 1028 : 257 ≈ 900 : 300 = 3
2.Подбираем частное, начиная с приближенного значения: 257 · 3 = 771, 771 < 1028, значит, 3 не подходит.
Поскольку при умножении на делитель у нас получилось число меньшее 1028, значит, необходимо для проверки взять число больше 3, а именно — 4. 257 · 4 = 1028, значит, 4 подходит.
3.Делаем вывод: 1028 : 257 = 4.
§ 2 Прикидка частного
Важно отметить, что если при умножении приближенного значения частного на делитель, получается число большее делимого, то необходимо для проверки взять число меньшее приближенного.
Покажем это на нашем примере:
1.Выполняем прикидку частного: 1028 : 257 ≈ 1000 : 200 = 5
2.Подбираем частное, начиная с приближенного значения: 257 · 5 = 1285, 1285 > 1028, значит, 5 не подходит. Поскольку при умножении на делитель у нас получилось число большее 1028, значит, необходимо для проверки взять число меньше 5, а именно — 4:
257 · 4 = 1028, значит, 4 подходит.
3.Делаем вывод: 1028 : 257 = 4.
Рассмотрим еще один пример 284 : 81
1.Выполняем прикидку частного: 284 : 81 ≈ 240 : 80 = 3
2.Подбираем частное: 81 · 3 = 243 – не подходит, 81 · 4 = 324 – не подходит. Проверять другие числа не имеет смысла, так как при увеличении числа произведение тоже будет увеличиваться, а при уменьшении – уменьшаться. Ни тот, ни другой вариант нам не подходит. Значит, 284 на 81 нацело разделить нельзя. 324 больше делимого 284, значит, 4 частным не является. 243 меньше делимого 284, значит, 3 является неполным частным чисел 284 и 81.
3.Делаем вывод:при делении 284 на 81 получаем неполное частное 3 и остаток 284 – 81 · 3 = 41, причем остаток должен быть меньше делителя, 41 < 81. 284 : 81 = 3 (ост. 41)
Деление с остатком оформляют следующим образом.
§ 3 Краткие итоги урока
Подведем итоги этого урока:
Для того чтобы выполнить деление на двузначное, трехзначное, четырехзначное и т.д. число, необходимо:
1.выполнить прикидку частного;
2.подобрать частное путем умножения на делитель, начиная с найденного приближенного значения частного.
Список использованной литературы:
- Петерсон Л.Г. Математика. 4 класс. Часть 1./Л.Г. Петерсон. – М.: Ювента, 2014
- Математика. 4 класс. Методические рекомендации к учебнику математики «Учусь учиться» для 4 класса. / Л.Г. Петерсон . – М.: Ювента, 2014.
- Зак С.М. Все задания к учебнику математики для 4 класса Л.Г. Петерсон и комплекту самостоятельных и контрольных работ. ФГОС. – М.: ЮНВЕС, 2014.
- CD-ROM. Математика. 4 класс. Сценарии уроков к учебнику к 1 части Петерсон Л.Г. – М.: Ювент, 2013.
Представим себе такую историю…
– И как же мне узнать-то? – задумался Саша.
– Что случилось? – поинтересовался у друга
Паша.
– Мы с родителями собрали 27 литров берёзового
сока, – начал рассказывать Саша. – Мама сказала к вечеру подготовить
трёхлитровые банки, чтобы закатать сок.
– Здорово! – обрадовался за друга Паша. –
Берёзовый сок очень полезный! Так, а что ты там не мог узнать?
– Не могу понять, сколько мне нужно
подготовить банок, – расстроенно ответил Саша.
– Ну, давай подумаем вместе! – предложил
Паша. – Тебе нужно подготовить трёхлитровые банки, то есть банки, в которые
поместится 3 литра сока. Правильно?
– Да! – ответил Саша.
– Всего вы собрали 27 литров берёзового сока,
– продолжил рассуждать Паша.
– Всё верно! – подтвердил Саша.
– Хорошо! – продолжил Паша. – Значит, надо
найти такое число, которое при умножении на 3 даст 27.
– Так это
же легко, –
сказал Саша. – Если 9 умножить на 3, то получится 27.
– Значит, тебе нужно подготовить 9 банок! –
закончил Паша.
– И что, каждый раз так делают? –
поинтересовался Саша. – Если в жизни встретятся подобные задачки, нужно будет
искать число, которое при умножении с известным числом даёт нужное число?
– Не знаю! – задумался Паша. – А давай
спросим у Электроши.
– Ребята, прежде чем я вам расскажу, как
решать подобные задачки, давайте немного разомнёмся и выполним устные задания,
– предложил Электроша.
– Давайте сверимся! Посмотрите, что у вас
должно было получиться!
– А теперь вернёмся к вашему вопросу, – предложил
Электроша. – Вы всё правильно посчитали и верно
заметили, что для того, чтобы узнать, сколько нужно подготовить трёхлитровых
банок, нужно найти такое число, которое при умножении на 3 даст 27. То есть вы
по одному из множителей и заданному произведению нашли второй множитель. В
таких случаях говорят о делении.
– Запомните! – сказал Электроша. – Действие, с помощью которого по произведению и
одному из множителей находят другой множитель, называют делением.
Действие деления определяют с помощью действия умножения. Например, 27
разделить на 3 – значит найти такое число, которое при умножении на 3 даёт
число 27. Имеем: 9 умножить на 3 равно 27, поэтому 27 разделить на 3 равно 9.
Вообще, для натуральных чисел
,
и
равенство
верно, если верно равенство
.
В равенстве число
называют делимым, число
– делителем, число
и саму запись
– частным.
Частное показывает, во сколько раз число
больше числа
или во сколько раз число
меньше числа
.
– Электроша, а я
слышал, что на 0 делить нельзя, – перебил Паша. – Это правда?
– Давайте порассуждаем, – предложил Электроша. – Возьмём какое-нибудь число, например
7. Что значит разделить 7 на 0?
– Это значит найти такое число
, которое при умножении на 0 даёт 7, – предположил Саша.
– Но ведь мы знаем, что если любое число
умножить на 0, то всегда получится 0, – возмутился Паша.
– Верно! – подтвердил Электроша.
– И это нам говорит, что никакое натуральное число невозможно разделить на 0.
Следовательно, вычислить частное 7 и 0 нельзя.
Запомните! На нуль делить нельзя.
– Электроша, а 0 можно
разделить на какое-нибудь число? – поинтересовался Саша.
– Давайте опять порассуждаем, – предложил Электроша. – Что значит разделить 0 на число
?
– Это значит найти такое число
, которое при умножении на
даст 0, – предположил Паша.
– Хорошо! – согласился Электроша.
– Тогда скажите, можно ли найти такое число ?
– Так это всем понятно, что можно, – начал
Саша. – Сюда подойдёт число 0. Ведь 0 умножить на равно 0.
– Молодец! – похвалил Сашу Электроша. – Запомните! При делении нуля на
натуральное число частное равно нулю. Также для любого натурального числа верны следующие равенства:
,
,
. Первое равенство говорит, что деление числа
на единицу результатом имеет само число. Второе – деление числа на само себя
имеет результатом число один. Последнее равенство выполняется при всех
натуральных числах, кроме , так как на ноль делить нельзя.
– Электроша, а как
проверить, правильно ли выполнено деление? – спросил Паша.
– Вообще,
для того чтобы убедиться в правильности выполнения деления, существует два
способа, – сказал Электроша. – Первый способ: нужно перемножить делитель и
частное, в результате должно получиться делимое. Второй способ: нужно разделить
делимое на частное, в результате должен получиться делитель.
– А теперь давайте попробуем найти частное от
деления чисел 126 126 и 231.
– Ого! Какие большие числа! – удивились
ребята. – Тут нам без калькулятора не обойтись.
– Ребята, всё гораздо проще, чем кажется на
первый взгляд, – успокоил ребят Электроша. – Вы уже
умеете делить уголком многозначное число на двузначное. Точно так же выполняют
и деление любых многозначных чисел. Такой способ поможет быстро и без ошибок
выполнить вычисление.
– Итак, запишем числа рядом на одной строчке,
а чтобы их не перепутать, поставим между ними уголок.
Под горизонтальной чертой будем писать частное или результат деления. Приступим
к делению. В данном случае, чтобы найти первую цифру частного, надо взять
первые четыре цифры делимого и получившееся число разделить на делитель 231.
– Электроша, а
почему мы берём именно первые четыре цифры делимого? – спросил Саша.
– Потому что если бы мы взяли хотя бы на одну
цифру меньше, то получившееся число, в данном случае 126, оказалось бы меньше
делителя 231, а такое деление мы не можем выполнить.
Итак, берём первые четыре цифры делимого и
попытаемся разделить получившееся число на 231. Наиболее подходящим здесь будет
число 5. Запишем его в строчке под делителем. Затем 5 умножим на 231. Получим 1155.
Получившееся число запишем под нашими четырьмя цифрами, что мы брали в качестве
делимого. Теперь от 1261 отнимем 1155. Получим 106. Число 106 меньше делителя,
значит, число 5 мы нашли верно. Теперь снесём следующую цифру делимого, то есть
2. Разделим число 1062 на 231. Возьмём по 4. Запишем четвёрку рядом с пятёркой
в частном. Затем 4 умножим на 231. Получим 924. И вычтем из 1062 число 924.
Получим 138. Видим: это число меньше делителя, значит, число 4 мы нашли верно.
Затем снесём последнюю цифру делимого. Получившееся число 1386 разделим на 231.
Берём по 6. 6 умножим на делитель и получим 1386. Выполним вычитание. Получим 0.
Деление закончено. Следовательно, 126 126 разделить на 231 равно 546.
– А теперь давайте решим несколько уравнений: ,
,
– предложил Электроша.
Итак, первое уравнение .
– Для того чтобы найти корень этого
уравнения, нужно вспомнить правило нахождения неизвестного множителя, – начал
Саша. – Чтобы найти неизвестный множитель, надо произведение разделить на
известный множитель. Получаем, что .
– Молодец! – похвалил Сашу Электроша. – Следующее уравнение .
– А здесь
нам нужно воспользоваться правилом нахождения неизвестного делимого, – сказал Паша, – чтобы найти неизвестное
делимое, надо делитель умножить на частное. Тогда получаем, что
.
– Правильно! – подтвердил Электроша.
– И осталось решить последнее уравнение: .
– В этом уравнении нам нужно найти делитель,
– начал рассуждать Cаша, – значит, воспользуемся правилом нахождения неизвестного делителя:
чтобы найти неизвестный делитель, надо делимое разделить на частное. Получаем, что .
– А теперь, ребята, давайте посмотрим, как вы
всё поняли, и выполним несколько заданий.
Задание первое: скорость моторной лодки 28 км/ч,
а скорость течения реки в 14 раз меньше. Какое расстояние по течению реки
пройдёт лодка за 4 часа?
Решение: сначала найдём скорость течения
реки. Для этого 28 разделим на 14. Получим, что скорость течения реки 2 км/ч.
Затем вычислим скорость моторной лодки по течению реки. Для этого к скорости
моторной лодки прибавим скорость течения реки. Получим 30 км/ч. И осталось
узнать, какое расстояние пройдёт моторная лодка по течению реки за 4 часа. 30 умножим
на 4. Получаем, что моторная лодка за 4 часа пройдёт 120 км по течению реки.
Следующее задание: из двух городов,
расстояние между которыми 260 км, одновременно вышли два поезда в одном
направлении. Скорость шедшего впереди поезда 50 км/ч, а скорость шедшего позади
поезда 70 км/ч. Через сколько часов после выхода второй поезд догонит первый?
Решение: для начала вычислим, на сколько
уменьшается расстояние между поездами каждый час. Для этого от 70 отнимем 50.
Получим 20. А затем вычислим время, за которое второй поезд догонит первый. 260
разделим на 20. Получаем, что второй поезд догонит первый поезд через 13 часов.
Занимаясь с учениками младших и средних классов, я часто вижу у них затруднения в быстром нахождении нужной цифры частного при выполнении промежуточных вычислений действия деления или непосредственно деления многозначных чисел. А между тем, этот навык достаточно простой, и освоив его, любые вычисления, связанные с делением, станут более легкими и быстрыми.
Как узнать, будет ли частное однозначным
Прежде всего, нужно научиться узнавать, получится в результате деления однозначное или многозначное число?
Чтобы это определить, нужно в уме быстро умножить делитель на 10 (самое маленькое многозначное число).
Если полученное произведение больше делимого, тогда частное получится меньше десяти, а значит, оно – однозначное число, а если делимое окажется больше, то частное будет точно больше десяти, а значит, оно – многозначное.
Рассмотрим пример ( textcolor{red} {396 div 33}).
33 на 10 – это 330; так как 330 меньше чем 396, следовательно, частное от деления 396 на 33 обязательно не будет однозначным числом.
Теперь другой пример ( textcolor{red} {396 div 66}).
66 умножить на 10, будет 660, а это больше чем 396. Значит, результат деления 396 на 66 обязательно будет однозначным числом.
Как найти однозначное частное
Рассмотрим два случая, когда в результате деления двух чисел получается однозначное число:
- делитель – однозначное число;
- делитель – многозначное число.
В случае, если делитель и частное – однозначные числа, на помощь приходит таблица умножения.
Например, частное от деления 54 на 9 будет 6, так как ( textcolor{red} {6 cdot 9 = 54} ).
Если поделить 54 на 8, частное будет 6, поскольку ( textcolor{red} {6 cdot 8 = 48} ), что меньше 54, а следующий множитель 7 даст нам результат больше, чем 54, так как ( textcolor{red} {7 cdot 8 = 56} ) , что нам не подходит. Значит, частное от деления 54 на 8 будет именно 6, и при этом в остатке получится ( textcolor{red} {54 – 48 = 6} ).
Во втором случае, если делитель – многозначное число, а частное – однозначное, то это частное находится при помощи испытаний одной или нескольких цифр.
Рассмотрим на примере: найдем однозначное частное при делении 36924 на 5955.
Для начала удостоверимся, действительно ли частное будет однозначным, воспользовавшись приемом, о котором я написал выше. 59550 больше чем 36924. Значит, все в порядке.
Конечно, можно пытаться последовательно умножать делитель 5955 на 2, 3, 4 и т.д., сравнивая результаты с делимым, но этот путь зачастую очень длинный и требует большого количества вычислений.
Я научу вас более простому способу.
1. В делителе берем цифру самого большого разряда (первую слева), а остальные цифры мысленно отбрасываем.
То есть, в нашем случае оставляем только 5 тысяч, а три цифры младших разрядов отбрасываем.
2. В делимом также мысленно отбрасываем столько же цифр младших разрядов, сколько отбросили в делителе.
В нашем примере мысленно отбрасываем от делимого 36924 три цифры справа, и получаем 36 тысяч.
3. Пытаемся разделить полученные числа в уме: делимое на делитель. Иными словами, ищем при помощи таблицы умножения такое число, которое при умножении на делитель даст результат равный или меньший, но как можно ближе к делителю. Частное исходных чисел будет равным или меньшим найденному на этом этапе числу. Меньшим оно может получиться потому, что мы отбросили мысленно несколько цифр.
В рассматриваемом примере нужно 36 разделить на 5. По таблице умножения видно, что это число 7, потому что: ( textcolor{red}{;7 cdot 5 = 35} ), а ( textcolor{red}{ 8 cdot 5 = 40} ), что уже больше чем 36. Значит, искомое частное или равно 7, или меньше 7.
4. Начинаем испытывать с полученного на прошлом этапе числа: умножаем его на изначальный делитель и сравниваем результат с делимым; если он оказался больше делимого, значит, это число не годится, и нужно испытывать следующее за ним меньшее число.
Умножим 5955 на 7; если получится число больше 36924, то попробуем число на единицу меньшее, то есть, 6:

Произведение ( textcolor{red}{ 5955cdot7 = 41685} ), что больше нашего делимого 36924, а произведение ( textcolor{red}{ 5955cdot6=35730}) меньше делимого, значит частное от деления 36924 на 5955 будет 6, при этом получится остаток ( textcolor{red}{36924– 35730= 1194}) .
Обратите внимание! Иногда можно найти первую цифру для испытания еще более удобным способом.
Если вторая слева цифра в делителе больше 5, можно на первом этапе цифру самого старшего разряда увеличить на 1, отбросив цифры младших разрядов, и уже на нее делить укороченное делимое, получившееся на втором этапе.
При этом во время проверки нужно проверяемую цифру частного умножить на изначальный делитель, и полученное произведение вычесть из делимого. Если останется число, большее чем делитель или равное ему, значит проверяемое частное мало, и следует взять следующее за ним большее число.
Так, в нашем примере после цифры 5 стоит 9, значит, можно увеличить 5 на единицу, и на него уже делить число 36. Получается число 6, что как показала проверка в предыдущем способе, является правильным ответом. Таким образом, мы отыскали его на одно действие быстрее.
Как видите, в этом приеме нет ничего особо сложного. Попрактиковавшись определенное количество времени, вы без труда сможете быстро и достаточно легко проводить необходимые вычисления.
Вам также пригодится:
Содержание материала
- Определение частного чисел (деление)
- Видео
- Неполное частное
- Как найти частное чисел
- Проверка деления умножением
- Увеличение или уменьшение делимого
- Нахождение значения частного чисел
- Деление с остатком
Определение частного чисел (деление)
Частное чисел — это результат получаемый при определении количества содержания одного числа в другом. Проще говоря это обычное деление. При этом общепринятые оперируемые понятия для частного это делимое, делитель и само частное — результат.
Пример. Найти частное чисел:
1) 20:2=10;
2) 35:7=5.
Ответ: 20:2=10 и 35:7=5.
Это был самый простой пример. Все самое интересное впереди! Проблемы с делением начинаются тогда, когда числа становятся большими и выходят за рамки таблицы умножения. Здесь приходится делить большое число по определенному правилу. Такое деление еще называется деление в столбик.
Пример. Найти частное чисел:
1) 894:3=298
-894| 3__ 6 |298-29 27— 24 24 0
Ответ: 894:3=298
Видео
Неполное частное
Неполное частное – результат, который получился после деления с остатком.
Под делением с остатком понимается нахождение наибольшего целого числа, которое в произведении с делителем дает число, не превышающее делимое. Это искомое и называют неполным частным.
Разность между делимым и произведением делителя на неполное частное называется остатком, который всегда меньше делителя.
Например, 17 не делится без остатка на 5.
Наибольшее число, результат умножения которого на 5 не превосходит 17, это 3. 3 в данном случае является неполным частным.
Чтобы получить остаток, нужно из 17 вычесть произведение 3 и 5, то есть 17 – 3*5 = 2. Остаток – 2.
Как найти частное чисел
Пришли в цирк трое ребят: Вася, Коля и Оля. На входе их встречал клоун Бим, который дарил детям шарики. У него в руках было 6 шариков, но дарил он их за отгадки. Клоун спросил у ребят:
— Мне надо подарить вам шарики, какое математическое действие я буду применять?
— Деление! — быстро ответил Коля. — Ты же будешь делить шарики между нами.
Клоун хитро прищурился:
— А как называются члены деления?
— Мы недавно это изучали! — воскликнула Оля. — Всё количество шариков, которое ты будешь делить, называется делимое. У тебя сейчас 6 шариков, значит здесь делимое — 6!
— А то, на сколько ребят ты их разделишь, называется делитель, — вмешался Вася. — Нас трое ребят, значит делитель — 3!
Коля продолжил:
— У каждого из нас будет часть шариков, и результат от деления называется частным.
— Какое же здесь будет частное? — спрашивает Бим.
— Два! — не сговариваясь, хором ответили ребята.
— Правильно, каждому из вас достанется по два шарика, это и есть частное.
Ребята ответили на все вопросы Бима, и каждый получил по два шарика — как результат деления:
6 (делимое) : 3 (делитель) = 2 (частное).
Запишем цифрами:
6:3=2
| Делимое | Делитель | Частное |
| 6 | 3 | 2 |
В этом выражении 6 (делимое) стоит самым первым, 3 (делитель) — на втором месте. А частное (2) — после знака равенства справа.
Итак, частное — это число, которое получается в результате деления делимого на делитель.
Проверка деления умножением
— Я что-то не пойму. Это уже умножение, а не деление! — говорит Бим. — Выходит, что деление — действие обратное умножению. То есть, мы можем проверить деление умножением?
— Да, — ответил Бом.
Деление — действие, обратное умножению. Для того чтобы проверить деление, надо провести умножение.
Центр образовательных технологий Advance
Увеличение или уменьшение делимого
Некоторые другие соотношения вытекают из этих. Например, если увеличить или уменьшить делимое в n раз, то в результате частное также повысится или понизится в n раз соответственно.
Изложенное правило имеет такой вид:

Приведём пример:
12 ⁄ 2 = 6 и пусть n = 3.
Проведём увеличение и уменьшение делимого:
(12∗3) /2 = 6∗3 — увеличили делимое на 3, равенство верное: 36 / 2 = 18;
(12 / 3) / 2 = 6 / 3 — уменьшили делимое на 3, равенство все равно верное: 4 / 2 = 2.
То есть, в три раза увеличив делимое, можно в три раза увеличить частное. Аналогично выполняется и уменьшение.
Нахождение значения частного чисел
Пример:
12 : 3 = 4 (в числе 12 4 раза содержится по 3)
15 : 5 = 3 (в числе 15 5 раз содержится по 5)
Нужно знать, что правильность определения частного от деления числа всегда можно проверить путем перемножения его на делитель, либо делимое поделить на частное и получить делитель.
Например:
20 : 4 = 5
Перемножим частное двух чисел на делитель и получим делимое:
4 * 5 = 20
Разделим делимое на частное и получим делитель:
20 : 5 = 4
Таким образом, мы доказали правильность определения частного.
Деление с остатком
Деление с остатком есть отыскание наибольшего целого числа, которое в произведении с делителем дает число, не превышающее делимое. Искомое число называется неполным частным. Разность между делимым и произведением делителя на неполное частное называется остатком. Он всегда меньше делителя.
19 не делится нацело на 5.Числа 1, 2, 3 в произведение с 5 дают 5, 10, 15,не превосходящие делимое 19,но уже 4 дает в произведении с 5 число 20, большее, чем 19.Поэтому неполное частное есть 3.Разность между 19 и произведением 3 · 5 = 15 есть 19 — 15 = 4;поэтому остаток есть 4.
Теги
Математика – царица наук. Она хоть и сложна, и многие боятся некоторых запутанных формул и вычислений, но все они состоят из простых арифметических действий сложения, вычитания, умножения и деления.
Производные операции от этих действий называются суммой, разностью, произведением и частным. Что такое частное в математике и каковы его главные свойства – будет подробно рассказано далее.
Основное свойство частного
Деление – это арифметическая операция, обратная умножению. С ее помощью можно просто узнать, сколько в первом числе содержится значений второго.
По аналогии с умножением, которое способно заменить собой многократное сложение, дробление способно заменить многократное вычитание.
Например, необходимо разделить 10 на 2. Это означает, что требуется узнать, сколько раз число 2 содержится в 10. Делая это вычитанием можно получить следующее:
10 — 2 — 2 — 2 — 2 — 2 = 0.
Проводя постепенное вычитание до нуля, можно определить, что двойка содержится в десятке ровно 5 раз и не образует остаток. Сделать это можно было однократно поделив два значения:
10 : 2 = 5.
Частное чисел – это итог процесса деления одного значения на второе. Пример:
28 : 7 = 4,
где 28 — делимое;
7 — делитель;
4 — частное.
Одно из важнейших правил деления частного, называемое основным свойством частного, заключается в том, что если делимое и делитель умножить или разделить на одно и то же число, то итог этой операции и, соответственно частное, не изменится:
При делении числа самого на себя результатом всегда будет единица, то есть справедливо равенство:
Справедливо и другое правило: если разделить определенную величину на единицу, то итогом процесса будет сама эта величина, то есть делимое:
Увеличение или уменьшение делимого
Некоторые другие соотношения вытекают из этих. Например, если увеличить или уменьшить делимое в n раз, то в результате частное также повысится или понизится в n раз соответственно.
Изложенное правило имеет такой вид:
Приведём пример:
12 ⁄ 2 = 6 и пусть n = 3.
Проведём увеличение и уменьшение делимого:
(12∗3) /2 = 6∗3 — увеличили делимое на 3, равенство верное: 36 / 2 = 18;
(12 / 3) / 2 = 6 / 3 — уменьшили делимое на 3, равенство все равно верное: 4 / 2 = 2.
То есть, в три раза увеличив делимое, можно в три раза увеличить частное. Аналогично выполняется и уменьшение.
Увеличение или уменьшение делителя
Следующее правило звучит так: если увеличить или уменьшить делитель в n раз, то результат деления понизится или повысится в n-нное количество раз:
Для примера требуется взять частное двух значений 54 и 6:
a / b = c и пусть n = 3.
Проведём увеличение и уменьшение делителя:
54 / (6∗3) = 9 / 3 — увеличили делитель в 3 раза, равенство верное: 54 / 18 =3;
54 / (6 / 3) = 9∗3 — уменьшили делитель в 3 раза, получаем равенство: 54 / 2 = 27.
Увеличив делитель в 3 раза, во столько же раз уменьшили частное. Уменьшив делитель в три раза, делитель, напротив, увеличился в три раза.
Проверить эти «законы» можно в любом онлайн калькуляторе или вручную в уме или на бумаге.
Данные правила являются фундаментальными и составляют базу арифметики, с которой начинается математика и остальные области знаний.