При этом трапеция обладает всеми свойствами четырехугольника. Поэтому запоминать надо свойства, которые характерны для трапеции.
Определения для трапеции:
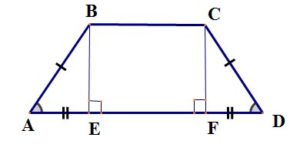
Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
Средняя линия трапеции — отрезок, который соединяет середины боковых сторон данной трапеции (на рис. MN). Средняя линия трапеции параллельна её основаниям и равна их полусумме. Средняя линия параллельна основаниям. Её длина находится по формуле: MN=(AD+BC)/2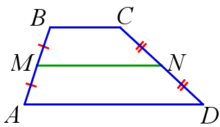
AD||BC, MN||AD, MN||BC,
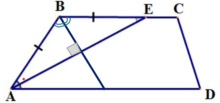
Равнобедренная (равнобокая) трапеция – трапеция, у которой боковые стороны равны (AB=CD).
В равнобедренной трапеции:
— углы при основании равны,
— проекции боковых сторон на основание равны: AE=FD,
— диагонали равны.
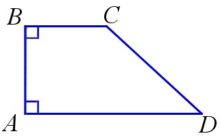
Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.
Свойства углов трапеции
- Свойства углов четырехугольника
- Сумма углов трапеции равна 360°
- Сумма внешних углов трапеции , взятых по одному при каждой вершине, равна 360°.
- Каждый угол трапеции всегда меньше суммы трёх остальных углов.
- Свойства углов трапеции
1. Сумма углов, прилежащих к боковой стороне, равна 180°: ∠A+∠B=180°, ∠C+∠D=180°
2. Каждая диагональ трапеции образует с её основаниями равные углы.
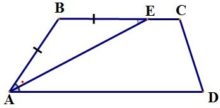
3. Биссектриса любого угла трапеции отсекает на ее основании отрезок, равный боковой стороне: AB=BE.
4. Биссектрисы смежных углов трапеции пересекаются под прямым углом.
Свойства сторон трапеции
- Свойства сторон трапеции (как у четырехугольника)
- Каждая сторона четырехугольника меньше суммы всех его других сторон.
- Сумма диагоналей меньше его периметра.
- Диагонали трапеции (как у четырехугольника)
- Диагонали пересекаются в одной точке.
- Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
- Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
- Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
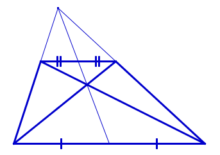
При пересечении диагоналей трапеции и продолжений её боковых сторон образуются подобные треугольники, прилежащие к основаниям.
Трапеция и окружность
В трапецию можно вписать окружность, если сумма её оснований равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.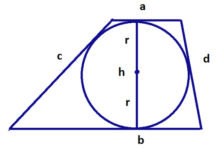
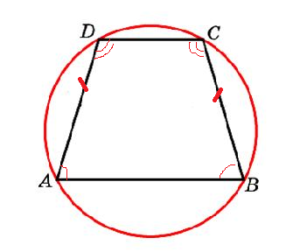
Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной. Центр описанной около трапеции окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон.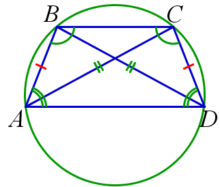
AB=CD ⇒ AC=BD;
AB=CD ⇒ ABCD вписанная
Основные формулы:
Периметр трапеции равен сумме длин всех его сторон:
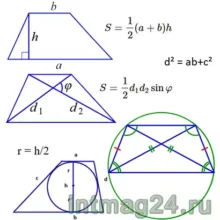
Площадь трапеции можно найти по двум формулам:
1. Половине произведения суммы её оснований на высоту трапеции.
2. Половине произведения её диагоналей на синус угла между ними.
Стороны и диагональ равнобокой трапеции: 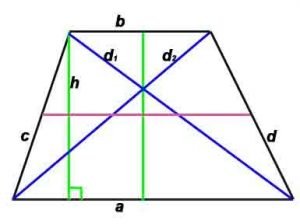
a,b — основания,
c,d — боковые стороны (с – боковые стороны в случае, если трапеция равнобокая),
d1, d2 –диагонали,
P-периметр,
S-площадь,
h -высота, проведенная к противоположной стороне
Трапеция вписанная в окружность и ее свойства
Какими свойствами обладает трапеция, вписанная в окружность?
Трапеция — это четырехугольник. А четырехугольник можно вписать в окружность только тогда, когда сумма противолежащих углов составляет 180 градусов.
А это возможно только в равнобокой трапеции. То есть, только равнобокую трапецию можно вписать в окружность.
Давайте вспомним свойства равнобокой трапеции.
Свойства трапеции равнобокой и трапеции, вписанной в окружность, часто можно встретить при решении задач. Поэтому нужно их помнить.
Хотите иметь справочные материалы со свойствами основных геометрических фигур всегда под рукой?
Тогда скачайте справочник в видеоформате.
«Видеошпаргалки по геометрии»
Интересная статья? Поделитесь ею пожалуйста с другими:
Трапеция. Формулы, признаки и свойства трапеции
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны
- Средняя линия — отрезок, соединяющий середины боковых сторон.
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Сторона трапеции
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a — h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a — c· cos α — d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
h = c· sin α = d· sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| 2 m | 2 m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
d 1 = √ a 2 + d 2 — 2 ad· cos β
d 2 = √ a 2 + c 2 — 2 ac· cos β
2. Формулы диагоналей через четыре стороны:
| d 1 = | √ | d 2 + ab — | a ( d 2 — c 2 ) |
| a — b |
| d 2 = | √ | c 2 + ab — | a ( c 2 — d 2 ) |
| a — b |
d 1 = √ h 2 + ( a — h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2
d 2 = √ h 2 + ( a — h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2
d 1 = √ c 2 + d 2 + 2 ab — d 2 2
d 2 = √ c 2 + d 2 + 2 ab — d 1 2
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
3. Формула площади через диагонали и угол между ними:
| S = | d 1 d 2 | · sin γ | = | d 1 d 2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c 2 — | ( | ( a — b ) 2 + c 2 — d 2 | ) | 2 |
| 2 | 2( a — b ) |
5. Формула Герона для трапеции
| S = | a + b | √ ( p — a )( p — b )( p — a — c )( p — a — d ) |
| | a — b | |
где
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p — a )( p — c )( p — d 1) |
где
a — большее основание
Окружность вписанная в трапецию
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Трапеция. Свойства трапеции
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то
Площадь
или где – средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Узнать ещё
Знание — сила. Познавательная информация
Трапеция вписана в окружность
Рассмотрим несколько направлений решения задач, в которых трапеция вписана в окружность.
Когда трапецию можно вписать в окружность? Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. Отсюда следует, что вписать в окружность можно только равнобокую трапецию.
Радиус окружности, описанной около трапеции, можно найти как радиус окружности, описанной около из одного из двух треугольников, на которые трапецию делит ее диагональ.
Где находится центр окружности, описанной около трапеции? Это зависит от угла между диагональю трапеции и ее боковой стороной.
Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания:
Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции лежит внутри трапеции.
Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием.
Радиус описанной около трапеции окружности можно найти по следствию из теоремы синусов. Из треугольника ACD
Из треугольника ABC
Другой вариант найти радиус описанной окружности —
Синусы угла D и угла CAD можно найти, например, из прямоугольных треугольников CFD и ACF:
При решении задач на трапецию, вписанную в окружность, можно также использовать то, что вписанный угол равен половине соответствующего ему центрального угла. Например,
Кстати, использовать углы COD и CAD можно и для нахождения площади трапеции. По формуле нахождения площади четырехугольника через его диагонали
В равнобедренном треугольнике AMD углы при основании равны. Внешний угол CMD равен сумме внутренних углов, не смежных с ним:
Трапеция — геометрическая фигура представляет собой выпуклый четырехугольник с параллельными
противоположными сторонами. Они называются основаниями. Две другие стороны — боковые.
Трапеция, у которой они одинакового размера, называется равнобедренной. Если одна из боковых сторон
образует у основания угол в 90 градусов-прямоугольной.
Прямая линия, проведенная от одного основания
к другому, именуется высотой трапеции. Величина ее высчитывается делением суммы оснований на 2.
Диагонали — это отрезки, соединяющие противоположные углы фигуры. У равнобедренной трапеции
они равны по длине. Средняя линия-прямая, делящая пополам боковые стороны.
- Угол трапеции при основании через высоту и прилегающую
боковую сторону - Угол трапеции через нижнее основание, боковую сторону и
диагональ - Угол равнобедренной трапеции через нижнее основание,
среднию линию и боковую сторону - Угол равнобедренной трапеции через среднию линию, верхнее
основание и боковую сторону - Острый угол при нижнем основании прямоугольной трапеции
через высоту и два основания - Острый угол при нижнем основании прямоугольной трапеции
через два основания и боковую сторону
Угол трапеции при основании через высоту и прилегающую боковую сторону
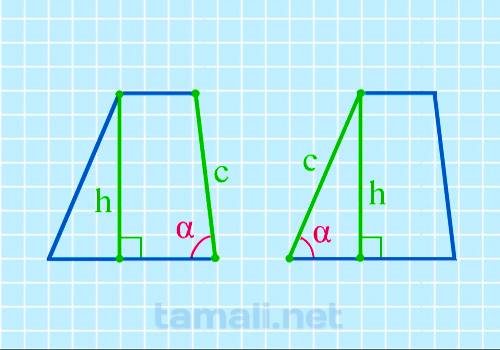
Введем обозначения: h-высота, с — боковая сторона. Угол трапеции α при основании вычисляется с
помощью формулы
sin α = h/с
где: h — высота трапеции, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Заменим буквенные обозначения условными цифрами. Пример: если высота равна
9см, боковая сторона-11см, получим: sin α = 9 / 11 = 0,818 , отсюда α =
55º. Указанное значение находим в таблице синусов. Данный показатель синуса угла соответствует
величине 55 градусов.
Через нижнее основание, среднию линию и боковую сторону в равнобедренной трапеции
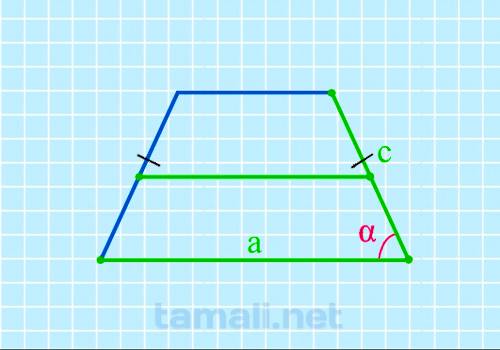
Угол равнобедренной трапеции через нижнее основание, среднюю линию и боковую сторону находится по
формуле:
cos α = (2a-2m) / 2c
где а — нижнее основание, m — средняя линия, с — боковая сторона.
Цифр после
запятой:
Результат в:
Пример.Заменим буквы условными цифровыми значениями. Если нижнее основание равно 8
см, средняя линия-6, а боковая сторона-4,8 см, то косинус угла равен 0,41666, что соответствует 65
градусам. cos α = (2 * 8 — 2 * 6) / 2 * 4,8 = 0, 41666, отсюда α =
65º. Равнобедренная трапеция — геометрическая фигура с нижними острыми углами. Это ее
особенность.
Угол трапеции, зная размер нижнего основания, боковой стороны и диагонали
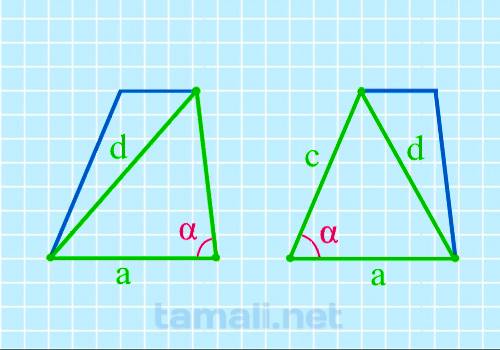
Если известны эти величины, воспользуемся формулой:
cos α= (a²+c²-d²) / 2ac
где а-нижнее основание, d-диагональ, с-боковая сторона.
Цифр после
запятой:
Результат в:
Пример. При условной величине нижнего основания 4 см, диагонали — 5.7 см,
боковой стороны — 4,4 см косинус равняется 0,081534, что соответствует углу 85 градусов по
таблице функций. cos α= (4² + 4,4² — 5,7²) / 2*4*4,4 = 0,081534,
отсюда α = 85º.
Через среднюю линию, верхнее основание и боковую сторону в равнобедренной трапеции
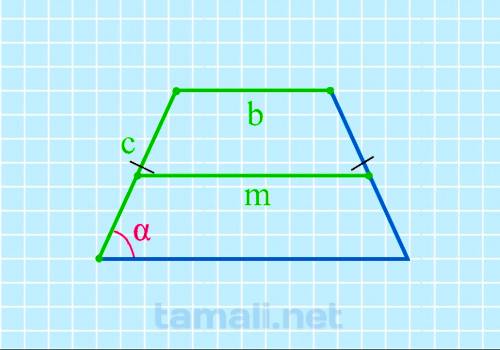
Нахождение угла равнобедренной трапеции через среднюю линию, верхнее основание и боковую сторону
выполняется по предложенной формуле:
cos α = (2m-2b) / 2c
где m — средняя линия, b — верхнее основание, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Введем условные цифровые значения. Допустим, что у равнобедренной трапеции
верхнее основание равно 4 см, средняя линия-6, боковая сторона-4 см. Косинус составляет 0,5.
Значение соответствует 60 градусам по таблице Брадиса. cos α = (2 * 6 — 2 * 4) / 2 * 4 = 0,5,
отсюда α = 60º
Вычисление острого угла при нижнем основании, если известны величины обоих оснований и боковой
стороны в прямоугольной трапеции
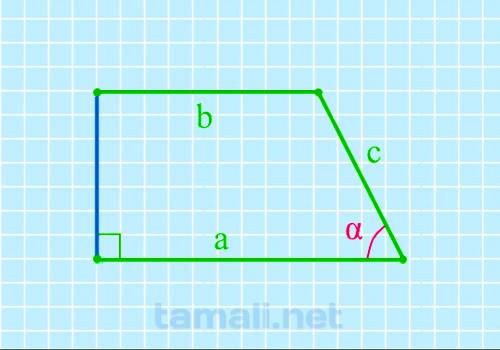
Находится по формуле
cos α = (a — b) / c
где a,b — основания, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Если буквенные выражения заменить условными цифровыми, получится наглядный
пример вычисления. Допустим, длина нижнего основания а 8 см, верхнего b-5,8 см, размер боковой
стороны с-4,8. Подставив в формулу цифровые значения, получим итог: косинус равен 0,45833.
Сравниваем показатель с таблицей вычисления Брадиса: он соответствует углу 63 градуса. cos α=(8 — 5,8) / 4,8 = 0,45833, отсюда α = 63º
Острый угол при нижнем основании, зная высоту и размеры двух оснований прямоугольной трапеции
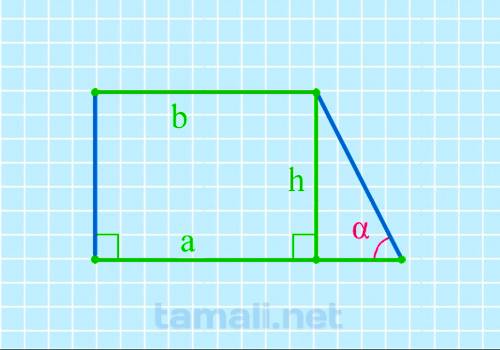
При известных указанных величинах воспользуемся следующей формулой:
tg(α) = h / (a-b)
где h — высота, a,b — верхнее и нижнее основания.
Цифр после
запятой:
Результат в:
Пример. Введя условные цифровые значения h = 15, a = 11, b = 10 получим tg(α) = 15 / (11-10) = 15. При вычислении получим значение тангенса: 15.
По таблице функций показатель соответствует 86 градусам.
Следует знать несколько закономерностей данной геометрической конструкции. У трапеции четыре угла,
общая сумма которых составляет 360 градусов.
Равнобедренная отличается двумя равными острыми, прилегающими к нижнему основанию, и тупыми
одинаковой величины-к верхнему. У прямоугольной трапеции два угла по 90 градусов, другие —
острый и тупой. Если он прилегает к нижнему основанию, величина такого угла определяется делением
высоты на разность между нижним и верхним основаниями. Угол трапеции при основании равен отношению
высоты к боковой стороне.
Какими могут быть углы трапеции?
рисунок 1
Как и все другие четырехугольники и многоугольники, которые изучаются в школьном курсе, трапеция — выпуклый четырехугольник. Поэтому сумма углов трапеции равна 360º (речь идет о внутренних углах).
То есть для трапеции ABCD ∠A+∠B+∠C+∠D=360º.
Поскольку основания трапеции лежат на параллельных прямых, сумма углов трапеции, прилежащих к боковой стороне, равна 180 градусам.
Для трапеции ABCD (рисунок 1)
∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB),
∠C+∠D=180º (как внутренние односторонние при AD ∥ BC и секущей CD).
Следовательно, если один из углов, прилежащих к одной боковой стороне, острый, то другой — тупой. Если один из этих углов прямой, другой — тоже прямой.
Суммы углов, прилежащих к боковым сторонам трапеции, равны:
∠A+∠B=∠C+∠D
Могут ли углы трапеции, взятые в последовательном порядке, относиться как
1) 7:3:5:2?
Нет, поскольку 7k+3k≠5k+2k и 7K+2k≠3k+5k.
2) 5:4:6:3?
5k+4k=6k+3k, следовательно, углы трапеции могут быть пропорциональны этим числам.
На рисунке 1 углы прилежащие к основанию AD, оба острые, углы, прилежащие к основанию BC, оба тупые. В паре противолежащих углов ∠A и ∠С, ∠B и ∠D один — острый, другой — тупой.
Существует ли трапеция, у которой два противолежащих угла обо тупые или оба острые?
рисунок 2
Да, такая трапеция существует.
Например, трапеция, изображенная на рисунке 2.
Существует ли трапеция, у которой два противоположных угла оба прямые? Противоположные углы равны?
Нет, такой трапеции не существует (противоположные углы равны у параллелограмма).