Представим выпуклый пятиугольник в виде четырехугольника с добавленным к нему треугольником. Поскольку сумма углов четырехугольника так или иначе равна 360 градусов, а сумма углов треугольника — 180 градусов, методом простого вычисления 180+360 получаем число 540: именно 540 градусов — сумма углов пятиугольника.
автор вопроса выбрал этот ответ лучшим
chipmunk
[41.5K]
9 лет назад
Сумма углов пятиугольника равна 540 градусов.
Для справки:
У шестиугольника сумма углов — 720 градусов.
У семиугольника сумма углов -900 градусов.
У восьмиугольника сумма углов -1080 градусов.
У четырехугольника сумма углов -360 градусов.
У треугольника сумма углов -180 градусов.
Oleg74
[203K]
8 лет назад
Существует формула для вычисления суммы всех углов многоугольника, благодаря которой можно вычислить сумму углов любого многоугольника, будь то треугольник, или четырехугольник, или пятиугольник и т. д.
Эта формула выглядит так :
Сумма углов = ( n — 2 ) х 180 °.
Тогда сумма углов для нашего пятиугольника будет равна ( 5 — 2 ) х 180 = 3 х 180 = 540 °.
А можно применить для такого вычисления и еще один способ, который заключается в том, что мы наш пятиугольник можем разделить на треугольники, которых будет три, а так как в треугольнике сумма углов равна 180 °, то 3 треугольника умножаем на 180 и получаем те же 540 °.
88SkyWalker88
[429K]
8 лет назад
Пятиугольником, судя по его названию, называют многоугольник с пятью углами.
Сумму углов пятиугольника можно найти по следующей формуле:
( n — 2 ) х 180 °, где n — это количество углов в многоугольнике, в нашем случае это будет пять.
Получается: (5-2) х 180 = 3 х 180 = 540
У пятиугольника с равными углами каждый угол будет равняться 108°.
gematogen
[29.9K]
8 лет назад
Сумма углов любого пятиугольников стоит 540 градусов.
В среднем величина угла около 110 градусов.
Пятиугольники в математике встречаются часто, поэтому необходимо знать формулу, если не знаете сколько градусов в фигуре.
Формула для нахождения суммы градусов в n-угольнике: (n-2)*180 градусов.
Ksyusha26
[26.8K]
8 лет назад
Существует формула, в соответствии с которой можно определить, чему равна сумма углов любого многоугольника. (n-2)*180, где n-это количество углов в нашем многоугольнике. Применим формулу: (5-2)*180=540. Верным ответом на данный вопрос будет число 540
Знаете ответ?
Чему равна сумма углов пятиугольника
Пятиугольник представляет собой геометрическую фигуру, обладающую соответствующим количеством углов. При этом для него, как и для других видов многоугольников, действуют общие правила, касающиеся в том числе суммы величин углов.

Пятиугольник представляет собой геометрическую фигуру, обладающую пятью углами. При этом, с точки зрения геометрии, в категорию пятиугольников входят любые многоугольники, обладающие этой характеристикой, вне зависимости от расположения его сторон.
Пятиугольник фактически представляет собой многоугольник, поэтому для вычисления суммы его углов можно воспользоваться формулой, принятой для исчисления указанной суммы в отношении многоугольника с любым количеством углов. Указанная формула рассматривает сумму углов многоугольника как следующее равенство: сумма углов = (n — 2) * 180°, где n — число углов в искомом многоугольнике.
Таким образом, в случае, когда речь идет именно о пятиугольнике, значение n в данной формуле будет равно 5. Таким образом, подставляя заданное значение n в формулу, получается, что сумма углов пятиугольника составит 540°. Вместе с тем, следует иметь в виду, что применение этой формулы в отношении конкретного пятиугольника связано с рядом ограничений.
Дело в том, что указанная формула для многоугольника, имеющего пять углов, как и для остальных видов этих геометрических фигур, может применяться только в том случае, если речь идет о так называемом выпуклом многоугольнике. Он, в свою очередь, представляет собой геометрическую фигуру, удовлетворяющую следующему условию: все ее точки находятся по одну сторону от прямой, которая проходит между двумя соседними вершинами.
Это определение можно несколько упростить, отметив, что в этом случае геометрическая фигура не должна иметь вершин, направленных внутрь нее. Только в этой ситуации правило, гласящее, что сумма углов пятиугольника составляет 540°, будет верным. Одним из частных случаев выпуклого пятиугольника является правильный пятиугольник, все углы которого равны, причем каждый составляет 108 градусов. В геометрии он имеет особое название, связанное с его греческим корнем — пентагон.
Таким образом, существует целая категория пятиугольников, сумма углов в которых будет отличаться от указанной величины. Так, например, одним из вариантов невыпуклого пятиугольника является геометрическая фигура звездчатой формы. Звездчатый пятиугольник также можно получить, используя всю совокупность диагоналей правильного пятиугольника, то есть пентагона: в этом случае образовавшаяся геометрическая фигура будет носить название пентаграммы, которая обладает равными углами. В этом случае сумма указанных углов будет составлять 180°.
Источники:
- Выпуклый многоугольник
Многоугольник, выпуклый многоугольник, четырехугольник
Ирина Алексеевна Антоненко
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Понятие многоугольника
Определение 1
Многоугольником называется геометрическая фигура в плоскости, которая состоит из попарно соединенных между собой отрезков, соседние из которых не лежат на одной прямой.
При этом отрезки называются сторонами многоугольника, а их концы — вершинами многоугольника.
Определение 2
$n$-угольником называется многоугольник, у которого $n$ вершин.
Виды многоугольников
Определение 3
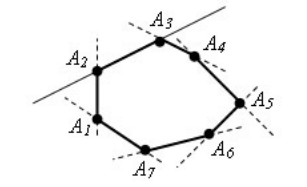
Если многоугольник всегда будет лежать по одну сторону от любой прямой, проходящей через его стороны, то многоугольник называется выпуклым (рис. 1).
Рисунок 1. Выпуклый многоугольник
Определение 4
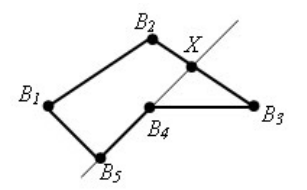
Если многоугольник лежит по разные стороны хотя бы одной прямой, проходящей через его стороны, то многоугольник называется невыпуклым (рис. 2).
Рисунок 2. Невыпуклый многоугольник
Сумма углов многоугольника
Введем теорему о сумме углов -угольника.
Теорема 1
Сумма углов выпуклого -угольника определяется следующим образом
[(n-2)cdot {180}^0]
Доказательство.
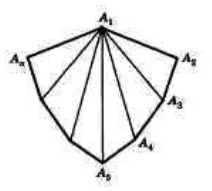
Пусть нам дан выпуклый многоугольник $A_1A_2A_3A_4A_5dots A_n$. Соединим его вершину $A_1$ со всеми другими вершинами данного многоугольника (рис. 3).
Рисунок 3.
При таком соединении мы получим $n-2$ треугольника. Просуммировав их углы мы получим сумму углов данного -угольника. Так как сумма углов треугольника равняется ${180}^0,$ получим, что сумма углов выпуклого -угольника определяется по формуле
[(n-2)cdot {180}^0]
Теорема доказана.
«Многоугольник, выпуклый многоугольник, четырехугольник» 👇
Понятие четырехугольника
Используя определение $2$, легко ввести определение четырехугольника.
Определение 5
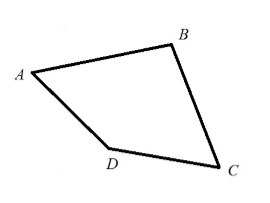
Четырехугольником называется многоугольник, у которого $4$ вершины (рис. 4).
Рисунок 4. Четырехугольник
Для четырехугольника аналогично определены понятия выпуклого четырехугольника и невыпуклого четырехугольника. Классическими примерами выпуклых четырехугольников являются квадрат, прямоугольник, трапеция, ромб, параллелограмм (рис. 5).
Рисунок 5. Выпуклые четырехугольники
Теорема 2
Сумма углов выпуклого четырехугольника равняется ${360}^0$
Доказательство.
По теореме $1$, мы знаем, что сумма углов выпуклого -угольника определяется по формуле
[(n-2)cdot {180}^0]
Следовательно, сумма углов выпуклого четырехугольника равняется
[left(4-2right)cdot {180}^0={360}^0]
Теорема доказана.
Примеры задач
Пример 1
Определить сумму углов выпуклого девятиугольника, семиугольника и двенадцатиугольника.
Решение.
Для решения будем пользоваться теоремой $1$. Получим:
Сумма углов выпуклого пятиугольника равняется
[left(5-2right)cdot {180}^0=3cdot {180}^0={540}^0]
Сумма углов выпуклого девятиугольника равняется
[left(9-2right)cdot {180}^0=7cdot {180}^0={1260}^0]
Сумма углов выпуклого двенадцатиугольника равняется
[left(12-2right)cdot {180}^0=10cdot {180}^0={1800}^0]
Пример 2
Сколько углов имеет выпуклый многоугольник, если сумма его углов равняется ${1620}^0$.
Решение.
Используя формулу задачи $1$, имеем
[left(n-2right)cdot {180}^0={1620}^0] [n-2=9] [n=11]
Ответ: $11$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 12.05.2023

triolana
+10
Решено
7 лет назад
Геометрия
5 — 9 классы
как найти сумму выпуклого б) пятиугольника б) сумиугольника в)девятиугольника
Смотреть ответ
1
Ответ
1
(1 оценка)
1
manikhina1
7 лет назад
Светило науки — 390 ответов — 2313 раз оказано помощи
Сумма углов выпуклого многоугольника вычисляется по формуле: 180*(n-2).
1)сумма углов выпуклого пятиугольника = 180*(5-2) = 540 градусов
2) сумма углов выпуклого семиугольника = 180*(7-2) =180*5= 900 градусов
3) сумма углов выпуклого девятиугольника равна 180*(9-2)= 180*7 = 1260 градусов.
(1 оценка)
https://vashotvet.com/task/9732622