Матрица – это прямоугольная таблица чисел, которая используется в линейной алгебре для решения систем уравнений и других математических задач. Во многих случаях матрицы являются невырожденными, то есть имеют обратную матрицу. Однако, существуют такие матрицы, которые не имеют обратной матрицы – они называются вырожденными.
Эти матрицы имеют много интересных свойств и поэтому интересны для изучения. Однако, определить, является ли матрица вырожденной или нет – задача довольно сложная и требует знаний математики. В этой статье мы рассмотрим, что такое вырожденная матрица и как ее можно определить.
Мы рассмотрим несколько методов определения, включая проверку на линейную зависимость строк и вычисление ее определителя. Также рассмотрим, как вырожденные матрицы используются в практических приложениях, например, для решения систем линейных уравнений и сжатия изображений.
Содержание
- Вырожденная матрица: определение и свойства
- Определение вырожденной матрицы
- Понятие вырожденной матрицы
- Как определить, что матрица является вырожденной?
- Свойства вырожденных матриц
- Как определить вырожденную матрицу?
Вырожденная матрица: определение и свойства
Вырожденная матрица – это матрица, у которой определитель равен нулю. Такая матрица не имеет обратной и не может быть решением системы линейных уравнений.
Важным свойством вырожденной матрицы является то, что ее строки или столбцы линейно зависимы между собой. Это значит, что одна из строк или столбцов может быть выражена через остальные.
- Обратная матрица вырожденной матрицы не существует.
- Количество уникальных решений линейной системы уменьшается при наличии вырожденной матрицы.
- Следствием вырожденности матрицы является ее невырожденность: если некоторые строки и/или столбцы вырожденной матрицы убрать, то новая матрица уже будет невырожденной.
Вырожденная матрица может возникать в различных задачах. Например, при решении системы линейных уравнений методом Гаусса, при нулевом значении определителя матрицы коэффициентов, мы имеем дело с вырожденной матрицей и не можем применить метод обратной матрицы или метод Крамера для нахождения решения.
Определение вырожденной матрицы
Понятие вырожденной матрицы
Вырожденная матрица — это матрица, у которой определитель равен нулю. Такая матрица не имеет обратной и ее система уравнений не имеет единственного решения. То есть, если рассматривать матрицу как систему линейных уравнений, то такая система может иметь бесконечное множество решений или не иметь их вовсе.
Как определить, что матрица является вырожденной?
Определить, что матрица является вырожденной, можно несколькими способами:
- Вычислить определитель матрицы (det(A)) и проверить, что он равен нулю;
- Попробовать выразить один из элементов матрицы через остальные элементы. Если это удастся сделать, то матрица является вырожденной;
- Проверить, что ранг матрицы меньше ее размерности. Если это так, то матрица является вырожденной.
Наличие вырожденной матрицы может быть обусловлено несколькими факторами, например, избыточностью системы уравнений, линейной зависимостью векторов или недостаточностью количества уравнений и переменных в системе.
Свойства вырожденных матриц
Вырожденная матрица — это квадратная матрица n на n, определитель которой равен нулю. У вырожденных матриц есть ряд характерных свойств и особенностей:
- В вырожденных матрицах не существует обратной матрицы — если матрица является вырожденной, то найти обратную к ней не получится;
- Вырожденная матрица не полного ранга, так как ее определитель равен нулю. Это означает, что в столбцах матрицы найдутся зависимые друг от друга вектора;
- Система линейных уравнений с матрицей-коеффициентом, являющейся вырожденной матрицей, не имеет единственного решения. Более того, она может не иметь решений вовсе;
- Вырожденные матрицы не являются некоторыми видами специальных матриц, таких как диагональные, верхнетреугольные или нижнетреугольные матрицы.
Понимание свойств вырожденных матриц помогает в решении линейных алгебраических задач и определении, используется ли в данной ситуации вырожденная матрица.
Как определить вырожденную матрицу?
Вырожденная матрица — это матрица, у которой определитель равен нулю. Определитель — это число, которое вычисляется для квадратной матрицы и является результатом сложения произведений элементов матрицы с определенными знаками.
Для определения вырожденной матрицы необходимо вычислить ее определитель. Если определитель равен нулю, то матрица будет являться вырожденной. Если определитель не равен нулю, то матрица будет невырожденной.
Также существует другой способ определения вырожденной матрицы, который заключается в проверке ее ранга. Ранг матрицы — это максимальное число линейно независимых строк в матрице. Если ранг матрицы меньше числа строк или столбцов, то матрица будет являться вырожденной.
Важно помнить, что вырожденная матрица не имеет обратной матрицы, то есть не может быть решена система уравнений, связанная с данной матрицей. Поэтому важно определять вырожденность матрицы при ее использовании в вычислениях.

Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Невырожденная и вырожденная матрицы
ОПРЕДЕЛЕНИЕ
Квадратная матрица называется невырожденной, если её определитель не равен нулю (
) и вырожденной, если
.
ПРИМЕР 1
| Задание | Определить вырожденные или невырожденные следующие матрицы
|
| Решение | Вычислим определители этих матриц
Определитель матрицы Так как |
| Ответ | матрица |
| Понравился сайт? Расскажи друзьям! | |
Нужна помощь с
решением задач?
Более 500 авторов онлайн и готовы помочь тебе прямо сейчас! Цена от 20 рублей за задачу. Сейчас у нас проходит акция, мы дарим 100 руб
на первый заказ.
Правило Саррюса (правило треугольника).
Пример
1:

–
2×1×
(–5)
+ 5×4×(–
4)
+ 3×2×(–
3)
–
(–
3)
×1× (–
4)
–
4×2×
(–
2)
–
5×3 × (–
5)
= 10 –
80
–18
–12
+16 +75 = –
9.
Пример
2:

45 + 8 ‒ 24 ‒ 60 + 6 ‒ 24 = ‒ 49.
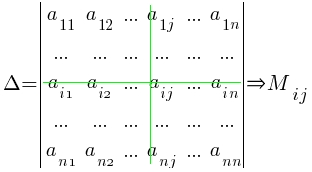
Минором
Mij
элемента aijквадратной
матрицы n
‒ го порядка называется определитель
(n
‒ 1) ‒ го порядка, полученный из данной
матрицы вычеркиванием i
‒ й
строки и j
‒ го
столбца, на пересечении которых стоит
данный элемент.
Пример:

M11
=
= 15 + 2 = 17;
M12
=
= –
6
–
6
= –12;
и т. д. всего 9 миноров.
Алгебраическим
дополнением Aijэлемента
aij
квадратной матрицы называется его
минор,
взятый со знаком (‒1)i+j.
Пример:
А
11 =
(–1)1+1
×
M11
=
17.
А
12 =
(–1)1+2
×
M12
=
‒ 1×M12
= 12.
А
13 =
(–1)1+3
×

4 ‒ 30= – 26; и т.д.
Теорема Лапласа
Определитель
квадратной матрицы равен сумме
произведений элементов любой строки
(столбца) на их алгебраические дополнения.

I
стр. =

(–1)
1+2
×


1+2
×
×


1+2×

Пример:

II
стр. = ‒ 2×(–1)2+1
×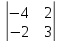
×
×(–1)
2+3×
2×(–12+4)+5×(9–12)–1×(–6+24) = 16–15–18= – 49.
Свойства определителей.
1.
Определитель равен нулю, если содержит:
—
нулевую строку или нулевой столбец;
—
две одинаковые строки (столбца);
—
две пропорциональных строки (столбца).
Пример:

0;


= I
× (-3).
2.
Общий множитель элементов любой строки
(столбца) можно выносить за знак
определителя.
Пример:

2×
3.
Определитель не изменится, если к
элементам любой строки (столбца) прибавить
элементы другой строки (столбца)
умноженные на одно число.
Пример:

× 5 + II; I × (‒2) + III; I × (‒ 4) + IV;
=


Вырожденные и невырожденные матрицы, обратная матрица.
Матрица
А-1называется
обратной к матрице A,
если при умножении ее на матрицу A,
как справа, так и слева, получится
единичная матрица.
А-1×A=A×
А-1=E
Матрица
называется невырожденной,
если ее определитель не равен 0, и
называется вырожденной,
если ее определитель равен 0.
Теорема.
Обратная
матрица А-1существует
только тогда, когда матрица невырожденная,
т.е. |A|
≠ 0.
Алгоритм
нахождения.
1.
Найти определитель матрицы А.
Если
│A│=
0, то обратная матрица не существует,
если │A│≠
0, то перейти ко второму шагу.
2.
Найти матрицу AT,
транспонированную к матрице А.
3.
Найти алгебраические дополнения
элементов матрицы AT
и составить из них матрицу Ã,
которая называется присоединенной.
Ã
=
4.
Обратную матрицу найти по формуле:
5.
Сделать проверку А—1
×
A
= E
Решение матричных уравнений.
Матричное
уравнение имеет вид:
A
× Х= B
Умножим
обе части уравнения на матрицу А—1
слева:
А-1×
A
×Х = А-1
×
В.
Так
как
А-1×А=Е,
то
Е×Х = А-1×В.
Так
какЕ
× Х=X,
то
Х= А-1×В
Пример:
Дано:
А
=

В
=

Найти:
X
‒?
Решение:
1)
│А│=
2)
AT=

3)
Ã=

4)
А-1
=



Х=
А-1×
B
=
Ответ:
Ранг матрицы, нахождение ранга матрицы.
Рангом
матрицы называется наивысший порядок
не равных нулю миноров этой матрицы.
Обозначается
rang
(A)
или r
(A).
Теорема
1.
Ранг матрицы не превосходит наименьшего
из ее размеров.
r(A)
≤ min (m; n)
Пример:
А2×3
=

r
(A)
≤ min
(2; 3) = 2, т. е. согласно теореме r
(A)
≤ 2.

3 + 24 = 27
0; r
(A)
= 2 (порядок ненулевого минора).
Теорема
2.
Ранг квадратной матрицы n-го
порядка равен ее порядку, если она не
вырожденная.
Примеры:
1)А3×3
=
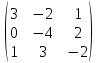
r
(A)
≤ 3.
│А│=
= 24 + 0 – 4 + 4 – 18 – 0 = 6
0


(A)
= 3.
2)А3×3
=
│А│=
0, т.к.
III = I × (– 3)

(A)
< 3.
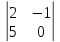
0 + 5 = 5
0

(A)
= 2 (порядок ненулевого минора).
Теорема
3.
Ранг матрицы не изменяется при элементарных
преобразованиях матрицы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Виды матриц.
- Матрица A размера m×n — это прямоугольная таблица чисел, расположенных в m строках и n столбцах
где aij (i =1, …, m; j =1, …, n) — это элементы матрицы A. Первый индекс i — это номер строки, второй индекс j — это номер столбца, на пересечении которых расположен элемент aij.
Сокращённое обозначение матрицы A=(aij)m×n. - Порядок матрицы — это число ее строк или столбцов.
- Главная диагональ квадратной матрицы — это диагональ, идущая из левого верхнего в правый нижний угол.
- Прямоугольная матрица — это матрица, у которой число строк не равно числу столбцов.
- Квадратная матрица — это матрица у которой число строк равно числу столбцов:
- Матрица-столбец — это матрица, у которой всего один столбец:
- Матрица-строка — это матрица, у которой всего одна строка:
- Диагональная матрица — это квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю.
- Единичная матрица — это диагональная матрица, у которой все диагональные элементы равны единице:
- Матрица квадратная диагональная:
- Треугольная матрица — это квадратная матрица, у которой все элементы, расположенные по одну сторону главной диагонали, равны нулю.
- Матрица верхняя треугольная:
- Матрица нижняя треугольная:
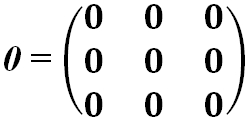
- Нулевая матрица — это матрица, все элементы которой равны 0:
- Операции над матрицами.
- Равенство матриц.
Две матрицы A (aij), B (bij) совпадают |A=B|, если совпадают их размеры и соответствующие элементы равны,
то есть при всех i, j aij=bij. - Сложение матриц.
Суммой двух матриц A=(aij)m×n и B=(bij) m×n одинаковых размеров называется матрица C=(cij)m×n=A+B тех же размеров, элементы которой определяются равенствами cij=aij+bij. Пример 1. - Умножение матрицы на число.
Произведением матрицы A=(aij)m×n на число λ ∈ R называется матрица B=(bij)m×n=λA, элементы которой определяются равенствами bij=λaij. Пример 2. - Умножение матриц.
Произведением матрицы A=(aij)m×k на матрицу B=(bij)k×n называется матрица C=(cij)m×n=A· B размера m×n, элементы которой cij определяются равенством
cij=ai1b1j+ai2b2j+ … aikbkj.
Таким образом, элемент матрицы C=A·B, расположенный в i-й строке и j-м столбце, равен сумме произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B. Пример 3. - Транспонированные матрицы.
Транспонированием матрицы А называется замена строк этой матрицы ее столбцами с сохранением их номеров.
Полученная матрица обозначается через A’ или AT. Пример 4.
Квадратная матрица называется симметричной, если A=A’, то есть для элементов выполнены равенства aij=aji. - Обратная матрица.
Квадратная матрица n–го порядка называется вырожденной, если определитель этой матрицы равен нулю, |A| = 0, и невырожденной, если |A| ≠ 0.
Матрица А-1 называется обратной матрицей для некоторой квадратной матрицы А, если выполняется соотношение:
Если матрица А-1 не вырождена, то существует, и притом единственная, обратная матрица А-1, равная, где АV = Aij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).
1)
2)
3)
4) - Алгоритм нахождения А-1 заключается в следующих пунктах:
1) Находим det A, проверяем det A ≠ 0.
2) Находим Mij — все миноры матрицы A.
3) Определяем
4) Строим матрицу алгебраических дополненийи транспонируем:
5) Делим каждый элемент матрицы на det A:Пример 5.
- Элементарные преобразования строк (столбцов) матрицы:
1) перестановка строк (столбцов);
2) умножение строки (столбца) на число α ≠ 0;
3) прибавление к элементам строки (столбца) матрицы элементов другой строки (столбца), умноженных на некоторое число. - Решение матричных уравнений.
Матричное уравнение — это уравнение, содержащее неизвестную матрицу X и известные матрицы A, B, …, .
Простейшие типы матричных уравнений:
1). Матрица A – квадратная и невырожденная,
|A| ≠ 0, следовательно, существует обратная матрица A-1.
Умножим уравнение на A-1 слева:
2). Матрица A – квадратная, |A| ≠ 0.
Умножим уравнение на A-1 справа:.
3). Матрицы A и B – квадратные, |A| ≠ 0, |B| ≠ 0.
Умножим уравнение на A-1 слева:
Умножим уравнение на B-1 справа:.
- Ранг матрицы.
Ранг матрицы A — это число, равное максимальному порядку отличных от нуля миноров.
Mk этой матрицы:
Матрицы называются эквивалентными, что обозначается
A ∼ B, если.
Ранг матрицы A вычисляется методом окаймляющих миноров или методом элементарных преобразований. - Метод окаймляющих миноров.
Пусть в матрице A элемент aij ≠ 0, тогда M1 ≠ 0 и r(A) ≥ 1. Окаймляем этот элемент элементами соседнего столбца и соседней строки (например, (j+1)–го столбца и (i+1)–й строки), получаем минор 2-го порядка:.
Если M2, то присоединяем другие строки и столбцы, перебирая все возможные миноры 2-го порядка.
Если все миноры второго порядка равны нулю, то r(A) = 1; если же существует хотя бы один минор 2-го порядка, отличный от нуля, то r(A) ≥ 1.
Выбираем отличный от нуля минор 2-го порядка M2 и окаймляем его элементами соседних строк и столбцов до минора 3-го порядка и так до тех пор, пока не будет выполнено условие: Mr ≠ 0, но все Mr+1 = 0. Пример 6. - Метод элементарных преобразований.
Элементарные преобразования матрицы не меняют ее ранга.
К элементарным преобразованиям матрицы относятся следующие: транспонирование; перестановка строк (столбцов); умножение строки (столбца) на число α ≠ 0; прибавление к элементам строки (столбца) матрицы элементов другой строки, умноженных на некоторое число; отбрасывание нулевой строки (столбца) матрицы.
Для определения ранга матрицы A методом элементарных преобразований следует:
1) Переставить строки и столбцы так, чтобы в верхнем левом углу матрицы был ненулевой элемент.
2) Все элементы первого столбца, кроме a11, обратить в ноль с помощью элементарных преобразований строк:
3) Переставить строки со 2–й по m и столбцы со 2–го по n так, чтобы a22 ≠ 0. Повторить операцию (2) со вторым столбцом: во втором столбце все элементы, кроме a12 и a22, обратить в ноль.
Окончательно после многократного применения указанной процедуры и отбрасывания нулевых строк преобразованная матрица будет иметь вид:
Тогда ранг матрицы A равен: rang A = rang Ã.
- Свойства определителей.
- Определитель квадратной матрицы А не меняется при транспонировании: |AT|=|A|.
- При перестановке местами любых двух строк (столбцов) определитель |A| меняет знак:
- Определитель, содержащий две одинаковые строки (столбца), равен нулю.
- Умножение всех элементов некоторой строки (столбца) определителя |A| на число k равносильно умножению определителя на это число:
- Если все элементы некоторой строки (столбца) определителя |A| равны нулю, то и сам определитель равен нулю (вытекает из предыдущего свойства при (k = 0):
- Если все элементы двух строк (столбцов) определителя |A| пропорциональны, то определитель равен нулю.
- Если каждый элемент некоторой строки (столбца) определителя представляет собой сумму двух слагаемых, то такой определитель можно представить в виде суммы двух определителей:
- Если к элементам какой-нибудь строки (столбца) определителя |A| прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель k, то величина определителя не изменится:
- Определитель |A| численно равен сумме произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения:
- Определитель произведения матриц А и В равен произведению их определителей:
.
- Определители n–го порядка.
- Минор Мij или Δij элемента аij ( иначе – дополнительный минор элемента аij) определителя n-го порядка — это определитель (n–1) порядка, полученный из исходного вычеркиванием i–й строки и j–го столбца, на пересечении которых стоит элемент aij.
- Алгебраическое дополнение Аij элемента аij — это его минор со знаком (-1)i+j, где i – номер строки, а j – номер столбца, на пересечении которых стоит элемент aij, Аij=(-1)i+jMij или Аij=(-1)i+jΔij. Пример 8.
Для определителей n-го порядка имеют место все перечисленные выше свойства определителей. - Правило выбора знака перед минором в алгебраическом дополнении:
- Определитель n-го порядка |A| численно равен сумме произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения.
- Метод сведения к треугольному виду.
Используя свойства (1–9), определитель преобразуют к виду, когда элементы, лежащие по одну сторону от главной диагонали, становятся равными нулю. Преобразованный таким образом определитель равен произведению элементов, лежащих на главной диагонали.
Формулы, уравнения, теоремы, примеры решения задач
Вырожденная матрица
Предмет
Высшая математика
Разместил
🤓 n-sorokina-96
👍 Проверено Автор24
квадратная матрица, определитель которой равен нулю
Научные статьи на тему «Вырожденная матрица»
Нахождение обратной матрицы методом Гаусса
Определение 1
Обратной матрицей матрицы $A$ называют такую матрицу $A^{-1}$, при умножении которой…
на исходную матрицу в качестве результата получается единичная диагональная матрица $E$, то есть матрица…
Квадратная матрица – это матрица, у которой количество строк и столбцов одинаково….
Вырожденной называют квадратную матрицу, определитель которой $det(A)$ равен нулю….
матрице:
$(A^T)^{-1} = (A^{-1})^T$;
Единичная обратная матрица равна единичной матрице:
$E = E^{-1}$

Статья от экспертов
Быстрый алгоритм проверки вырожденности ганкелевых матриц
Из результатов работ 2009-2010 годов Платонова В.П. (совместно с Беняш-Кривецем В.В.) следует, что в случае эллиптических полей эффективность алгоритмов вычисления нетривиальных единиц напрямую определяется эффективностью алгоритмов проверки вырожденности соответствующих ганкелевых матриц. В этой связи был разработан асимптотически наилучший рекурсивный алгоритм проверки вырожденности ганкелевых матриц сложности O(nlog 2 n), который не накладывает ограничений на невырожденность ведущих подматриц и для этого алгоритма вычислена мультипликативная константа 468.
Линейное программирование Maple
Квадратной матрицей называется матрица, имеющая одинаковое количество строк и столбцов….
Сингулярной или вырожденной матрицей называется квадратная матрица, имеющая определитель равный нулю….
Например, имеется исходная матрица:
Рисунок 1. Матрица….
Матрица….
Следом матрицы является сумма компонентов в диагонали матрицы.

Статья от экспертов
ХАРАКТЕРИСТИКИ РАЗЛИЧЕНИЯ СИСТЕМЫ СИГНАЛОВ С ВЫРОЖДЕННОЙ КОРРЕЛЯЦИОННОЙ МАТРИЦЕЙ
В статье рассматривается задача различения неортогональных сигналов с многопозиционной фазовой и амплитудно-фазовой модуляцией на фоне гауссовских помех. В качестве решающего правила выбран критерий максимального правдоподобия. При теоретическом анализе вероятностей ошибок решающего правила возникают многомерные нормальные интегралы с вырожденной корреляционной матрицей. Поскольку вычисление таких интегралов не разработано, на практике применяются или оценки вероятности ошибок в виде границ сверху, или эвристические приемы для некоторых частных случаев. Применение метода Монте-Карло для нахождения вероятностей ошибок в этом случае является нетривиальной задачей, поскольку формирование многомерных нормальных векторов, использующее разложение Холецкого вырожденной корреляционной матрицы, невозможно. В данной работе предложен способ вычисления многомерных нормальных интегралов с вырожденной корреляционной матрицей. Расчеты основаны на методе возмущения корреляционной матрицы системы си…
Повышай знания с онлайн-тренажером от Автор24!
- Напиши термин
- Выбери определение из предложенных или загрузи свое
-
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек

![Rendered by QuickLaTeX.com [D=left( begin{matrix} -2 & 6 \ 1 & -3 \ end{matrix} right), text{ } B=left( begin{matrix} -3 & 0 & 2 \ 3 & -1 & 0 \ -2 & 0 & 1 \ end{matrix} right)]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-4f57f28e35e4d2b969d0c007b2cba0c3_l3.png)
![Rendered by QuickLaTeX.com [B=left| begin{matrix} -3 & 0 & 2 \ 3 & -1 & 0 \ -2 & 0 & 1 \ end{matrix} right|=3+0+0-4-0-0=-1ne 0]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-8c63c3fd0802ea21925a00fd0052a048_l3.png)



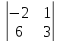







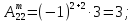






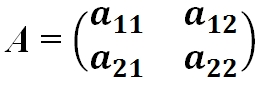
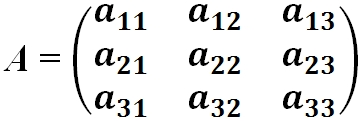
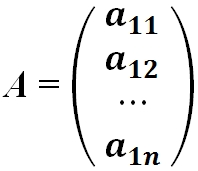
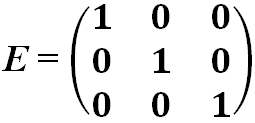
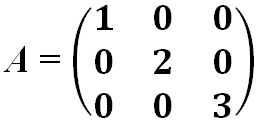
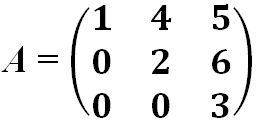
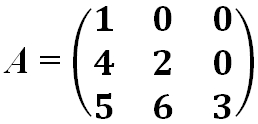

 , где АV = Aij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).
, где АV = Aij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).




 и транспонируем:
и транспонируем: 
 Пример 5.
Пример 5. . Матрица A – квадратная и невырожденная,
. Матрица A – квадратная и невырожденная,
 . Матрица A – квадратная, |A| ≠ 0.
. Матрица A – квадратная, |A| ≠ 0. .
. . Матрицы A и B – квадратные, |A| ≠ 0, |B| ≠ 0.
. Матрицы A и B – квадратные, |A| ≠ 0, |B| ≠ 0.
 .
.
 .
. .
.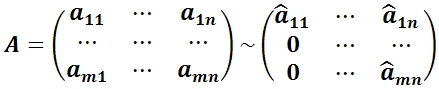
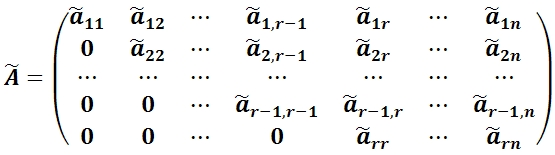







 .
.