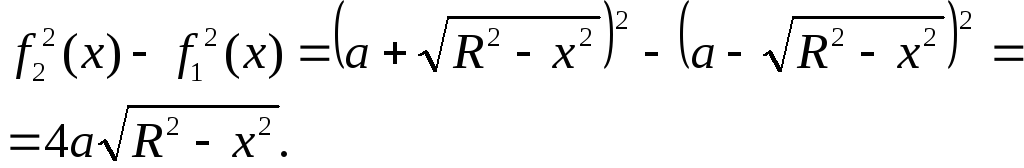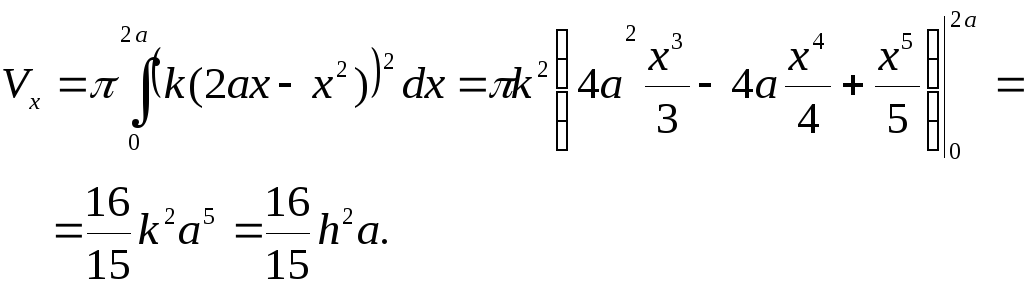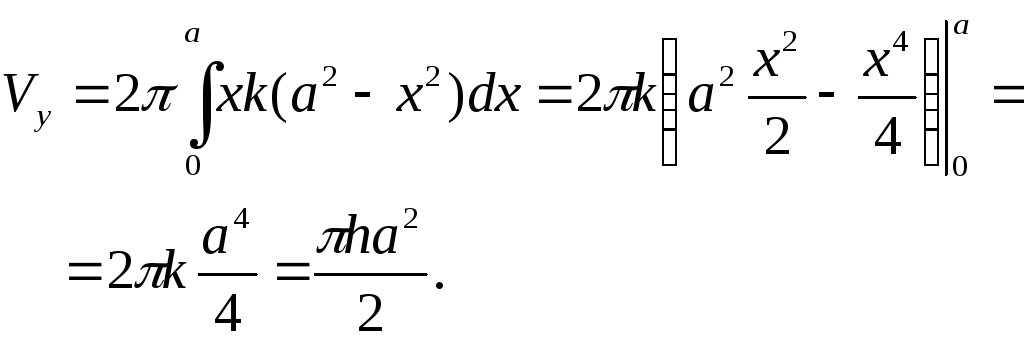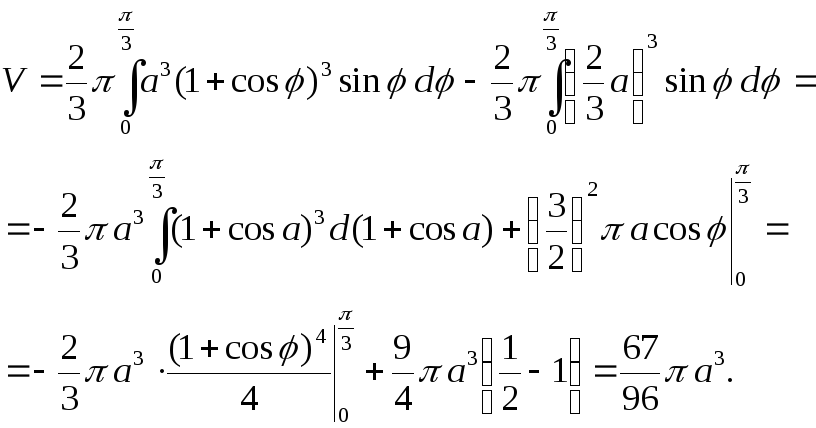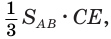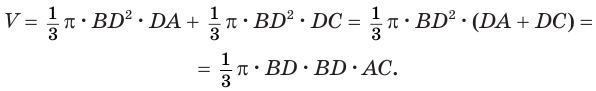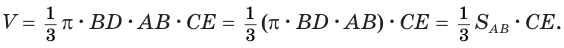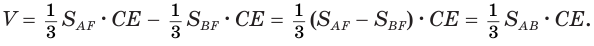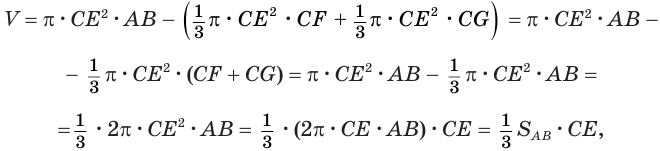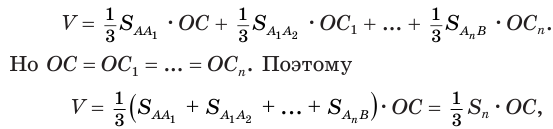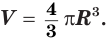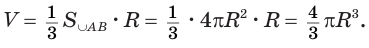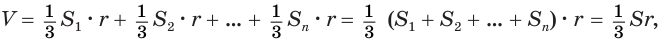Телом вращения называют пространственную фигуру, полученную в результате вращения некоторой плоской фигуры вокруг оси. Среди всех тел вращения выделяют цилиндр, конус и шар.
Цилиндром называют фигуру, полученную в результате вращения прямоугольника вокруг одной из его сторон (оси цилиндра).
Образующей цилиндра называют отрезок, соединяющий точки окружностей оснований цилиндра, и перпендикулярный диаметрам его оснований.
Высотой цилиндра называют перпендикуляр, заключенный между основаниями цилиндра.
На рисунке 9.66 прямая 







Объем цилиндра высоты 

Площадь основания цилиндра (

Площадь поверхности цилиндра находят по формуле:

Площадь боковой поверхности цилиндра находят по формуле:

где 


Конусом называют фигуру, полученную в результате вращения прямоугольного треугольника вокруг одного из катетов (оси конуса).
Образующей конуса называют отрезок, соединяющий вершину конуса с точкой окружности основания конуса.
Высотой конуса называют перпендикуляр, соединяющий вершину конуса с центром его основания.
На рисунке 9.67 прямая 




Усеченным конусом называют часть конуса, ограниченную его основанием и сечением, параллельным плоскости основания.
На рисунке 9.68 изображен усеченный конус.
Объем конуса высоты 

Площадь основания конуса (

Площадь поверхности конуса находят по формуле:

Площадь боковой поверхности конуса находят по формуле:

где 

Объем усеченного конуса находят по формуле:

где 


Площадь боковой поверхности усеченного конуса находят по формуле:

где 



Сферой называют фигуру, полученную в результате вращения полуокружности вокруг ее диаметра (рис. 9.69).
Шаром называют фигуру, полученную вращением полукруга вокруг его диаметра.
Сечение сферы плоскостью – окружность.
Сечение шара плоскостью – круг.
Сечение шара плоскостью, проходящей через центр шара, называют большим кругом (на рисунке 9.69 круг с центром в точке 

Касательной плоскостью к сфере (шару) называется плоскость, имеющая со сферой единственную общую точку (на рисунке 9.69 плоскость 

Касательная плоскость перпендикулярна радиусу сферы в точке касания.
Площадь сферы радиуса 

Объем шара радиуса

Выпуклый многоугольник вписан в сферу, если все его вершины лежат на поверхности сферы, и описан около сферы, если все его стороны касаются поверхности сферы.
Сферическим (шаровым) сегментом называют часть сферы (шара), отсекаемую плоскостью.
Высотой 

Шаровым сектором называют тело, полученное вращением кругового сектора вокруг одного из ограничивающих круговой сектор радиусов.
Высотой шарового сектора называют высоту части его сферической поверхности.
На рисунке 9.70 шаровой сектор получен в результате вращения кругового сектора вокруг радиуса 
Объем шарового сегмента находят по формуле:

Площадь сферической поверхности находят по формуле:

где 

Объем шарового сектора находят по формуле:

где 

Пример 1. Осевое сечение цилиндра – квадрат со стороной 

Решение. Так как осевое сечение квадрат (рис. 9.71), то 

По формулам 9.15 и 9.16 найдем объем цилиндра: 
По формулам 9.16 , 9.17 и 9.18 найдем площадь поверхности цилиндра: 
Ответ: 

Пример 2. Площадь боковой поверхности цилиндра равна 

Решение. Площадь боковой поверхности и объем цилиндра найдем по формулам 9.18 и 9.15 , где 

Тогда согласно условию задачи запишем: 
Разделим первое уравнение системы на второе и получим: 


Найдем 

Ответ: 
Пример 3. Найдите объем и площадь поверхности конуса, осевым сечением которого является правильный треугольник со стороной 
Решение. Так как 



По формулам 9.19 и 9.20 найдем объем конуса: 

По формулам 9.20 , 9.21 и 9.22 найдем площадь поверхности конуса: 

Ответ: 



Пример 4. Радиус основания конуса равен 

Решение. Рассмотрим конус радиуса 

Найдем длину окружности в основании конуса: 
Найдем длину дуги в развертке боковой поверхности конуса: 
Так как 


Из теоремы Пифагора: 

По формулам 9.19 и 9.20 найдем объем конуса: 
Ответ: 
Пример 5. Осевое сечение конуса – равнобокая трапеция с основаниями 


Решение. Имеем усеченный конус (рис. 9.74), радиусы оснований которого соответственно равны 




По формуле 9.24 найдем площадь боковой поверхности конуса: 
По формуле 9.23 найдем объем конуса:

Ответ: 

Пример 6. Периметр правильного шестиугольника, все вершины которого лежат на поверхности шара, равен 

Решение. Найдем сторону правильного шестиугольника, зная его периметр: 
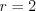
Объем шара находят по формуле 9.26 .
Так как 




Из теоремы Пифагора: 

Ответ: 
Пример 7. Сторона квадрата, описанного около шара, равна 

Решение. 1. Найдем диагональ квадрата, зная его сторону: 



2. Из теоремы Пифагора: 

3. Найдем высоту сферической поверхности:


4. По формуле 9.28 найдем площадь сферической поверхности:


Ответ: 
Пример 8. Равнобедренная трапеция с основаниями 


Решение. Рассмотрим равнобедренную трапецию 










Рассмотрим прямоугольный треугольник 


тогда 

Согласно формуле 


Согласно формуле 


Найдем площадь поверхности тела вращения: 

Ответ: 

1. В цилиндре умейте определять: радиус основания, высоту, образующую, осевое сечение.
2. В конусе умейте определять: радиус основания, высоту, образующую, осевое сечение.
3. Различайте шар и сферу (поверхность шара). Умейте определять: 1) центр, радиус и диаметр сферы; 2) в шаре: центр, радиус, диаметр, сечение, шаровой сегмент и шаровой сектор.
Тела и поверхности вращения. Шар. Цилиндр. Конус
Тела и поверхности вращения.
Шар. Цилиндр. Конус. Площади поверхности и объемы этих фигур.
Подробная теория с наглядными иллюстрациями и основные формулы.
Читай эту статью, здесь все это есть.
Всего за 15 минут ты полностью во всём разберешься!
Тело вращения – это тело в пространстве, которое возникает при вращении какой-нибудь плоской фигуры вокруг какой-нибудь оси.
Вот самый простой пример: цилиндр.
Берем прямоугольник и начинаем вращать его вокруг одной из сторон.
Смотри.
Было–вращаем–стало:
А теперь гораздо хитрее. Бывает так, что ось вращения находится далеко от фигуры, которая вращается.
Например, так:
Вращаем:
Что получится? Бублик. А по-научному – ТОР.
Ну и так вот можно любую фигуру вертеть вокруг любой оси, и будут получаться разные более или менее сложные тела вращения.
Ну, а поверхность вращения – это просто граница тела вращения. Ведь поверхность это всегда граница тела.
Здесь мы рассмотрим подробно несколько тел вращения. Те, которые встречаются в школьных задачах. Это шар, цилиндр и конус.
Шар
Шар – тело вращения, полученное вращением полуокружности вокруг диаметра.
Было–вращаем–стало:
Вообще-то есть и другое определение шара – через ГМТ (геометрическое место точек)
Шар – геометрическое место точек, удаленных от одной фиксированной точки на расстояние, не более заданного.
Скажу тебе по секрету, что, хоть второе определение и пугающее на вид, оно удобнее в обращении. Задумайся, ведь если тебя попросят сказать, что такое шар, ты скажешь что-то вроде:
«ну …там есть центр и радиус…», подразумевая, что все точки внутри шара находятся я на расстоянии не большем, чем радиус.
Ну, в общем, шар он и есть шар.
Названия, которые ты должен знать:
Незнакомое тебе, наверное, только одно.
Диаметральное сечение шара – сечение, проходящее через центр. Это сечение иногда еще называют большим кругом.
А вообще:
- Любое сечение шара – круг.
- Граница шара называется сфера. (Так же, как граница круга – окружность.)
Площадь поверхности сферы
( {{S}_{поверхности }}=4pi {{R}^{2}})
( R) – радиус
Откуда взялось? Умные математики придумали – это не так уж просто – придется просто запомнить.
Объем шара
( {{V}_{шара}}=frac{4}{3}pi {{R}^{3}})
( R) – радиус
Это еще одна хитрая формула, которую придется запомнить, не понимая, откуда она взялась.
Если ты знаком с производной, то можешь заметить это:
( {{V’}_{шара}}={{S}_{поверхности}})
И это не случайно! Но почему это так вышло, мы тоже здесь обсуждать не будем. Можешь попробовать доказать это сам!
Цилиндр
Цилиндр – тело, образованное вращением прямоугольника вокруг одной из сторон.
Вообще-то, полное имя этого тела – «прямой круговой цилиндр», но составители задач и мы вместе с ними по дружбе называем его просто цилиндром. Названия, относящиеся к цилиндру, такие:
Основания у цилиндра – это круги
Еще у цилиндра есть так называемая развертка.
Представь, что у нас от цилиндра осталась только боковая поверхность, и мы ее разрезали вдоль образующей и развернули.
Что получится? Представь себе, прямоугольник.
Развертка цилиндра – прямоугольник.
Площадь боковой поверхности цилиндра
( {{S}_{бок.}}=2pi RH)
( R) – радиус
( H) – высота, она же образующая.
Откуда взялась эта формула? Это как раз легко! Именно потому, что цилиндр можно развернуть, и получится прямоугольник ( 2pi Rcdot H).
Площадь этого прямоугольника и есть площадь боковой поверхности цилиндра.
Площадь прямоугольника, как мы хорошо помним равна произведению сторон, поэтому
( {{S}_{бок.}}=2pi RH)
Площадь полной поверхности цилиндра
Прибавляем теперь площадь двух кругов – оснований и получаем:
( {{S}_{полн .}}=2pi RH+2pi {{R}^{2}})
Можно вынести (хотя и не обязательно) ( 2pi R):
( {{S}_{полн .}}=2pi Rleft( H+R right))
Но эту формулу неудобно запоминать!
Гораздо проще запомнить, что полная поверхность – сумма боковой поверхности и еще двух кругов – оснований, а боковая поверхность – прямоугольник. И тогда ( {{S}_{полн .}}) можно вообще не запоминать, ты всегда сам напишешь, что
( {{S}_{полн .}}=underbrace{2pi RH}_{прямоугольник}+underbrace{2pi {{R}^{2}}}_{два круга})
Объем цилиндра
( V=pi {{R}^{2}}H)
( R) – радиус основания ( H) – высота
Это точно как у призмы и параллелепипеда!
( V={{S}_{основания}}cdot H), только у призмы и параллелепипеда ( {{S}_{основания}}) — это площадь многоугольника, а у цилиндра ( {{S}_{основания}}) — это площадь круга.
Конус
Конус – тело вращения, образованное вращением прямоугольного треугольника вокруг одного из катетов.
Было–вращаем–стало:
И опять же, полное название этого тела: «прямой круговой конус», но во всех задачах у нас говорится просто «конус».
Названия, относящиеся к конусу:
Что тут нужно твердо помнить?
- Основание корпуса – круг
- Все образующие конуса – равны.
Ясно ли это? Вроде должно быть ясно, ведь образующая – это гипотенуза (одна и та же!) Треугольника, который вращаем, а радиус основания – катет.
У конуса тоже есть развертка.
Снова представим, что основания нет, разрежем боковую поверхность вдоль образующей и развернём кулек. Что получится?
Представь себе сектор круга. Пусть длина образующей равна ( l).
Развертка конуса – сектор круга радиуса ( l)
Площадь поверхности конуса
Как найти площадь боковой поверхности корпуса? Вспомним о развертке, ведь для цилиндра все было просто именно с помощью развертки.
По формуле площади сектора ( {{S}_{бок.}}={{l}^{2}}cdot frac{alpha }{2}) Где ( alpha ) – угол при вершине в радианах.
И это уже формула. В некоторых задачах бывает дан именно угол при вершине в развертке конуса.
Но если все же даны только образующая и радиус основания, как быть?
Нужно осознать, что же такое дуга в развертке? Это бывшая окружность основания! Поэтому длина этой дуги равна ( 2pi R).
С другой стороны, длина этой же дуги равна ( alpha cdot l), так как это дуга окружности радиуса ( l). Поэтому
( alpha cdot l=2pi R)
Подставляем
( {{S}_{бок.}}={{l}^{2}}cdot frac{alpha }{2}=frac{l}{2}cdot alpha cdot l=frac{l}{2}cdot 2pi R)
Итак,
( {{S}_{бок.}}=pi Rl), где
( R) — радиус окружности основания,
( l) — длина образующей
Ну, и осталось площадь полной поверхности конуса. Прибавим к боковой поверхности площадь круга основания, и получаем:
( {{S}_{полн. }}=pi Rl+pi {{R}^{2}})
Можно вынести ( pi R):
( {{S}_{полн. }}=pi Rleft( l+R right))
Но, как и для цилиндра, не надо запоминать вторую формулу, гораздо проще всегда пользоваться первой.
Объём конуса
( V=frac{1}{3}pi {{R}^{2}}H)
( R) – радиус основания (
H) – высота
Это так же, как у пирамиды
( V=frac{1}{3}{{S}_{осн.}}cdot H), только
( {{S}_{осн. }}) — это не площадь многоугольника, а площадь круга.
А вот откуда взялась ( frac{1}{3})?, по-прежнему остается загадкой, потому что эта ( frac{1}{3}) получена в результате довольно хитрых рассуждений умных математиков.
А тебе нужно очень твердо запомнить, что в формулах объёма «треугольных» фигур: конуса и пирамиды эта ( frac{1}{3}) и есть, а в формулах параллелепипеда, призмы и цилиндра ее нет!
Бонус: Вебинары по стереометрии из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 14 Стереометрия. Расстояние между точками и от точки до прямой
В этом видео мы научимся «видеть» 3-мерное пространство и изображать 3-мерные объекты на бумаге (то есть на плоской поверхности).
Затем мы научимся двум основным вещам — находить расстояние между точками на таких рисунках, а также расстояние от точки до прямой.
На этих умениях строится всё дальнейшее изучение стереометрии. В общем это очень важное, базовое видео, с которого нужно начинать изучение стереометрии.
Не перескакивайте, не пропускайте его! Даже если вы знаете стереометрию, вы найдете для себя очень много полезного и нового в этом видео.
ЕГЭ 14. Стереометрия. Пирамида. Разбор варианта профильного ЕГЭ 2020
В этом видео:
- Как нарисовать шестиугольную пирамиду.
- Как подписать вершины пирамиды чтобы потом легче было решать задачу.
- Как исправить рисунок, если грани пирамиды сливаются.
- Доказательство пунктов А и Б, а также их правильная запись, которую примет любой проверяющий на ЕГЭ.
- Нахождение площади основания и объема пирамиды.
- Самое главное, на что нужно обратить внимание.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Определение
3. Тело
вращения – это тело, полученное вращением
плоской фигуры вокруг оси, не
пересекающей фигуру и лежащей с ней в
одной плоскости.
Ось вращения может
и пересекать фигуру, если это ось
симметрии фигуры.
Теорема
2. Пусть
криволинейная трапеция, ограниченная
графиком непрерывной неотрицательной
функции
,
осьюи отрезками прямых
и
вращается вокруг оси
.
Тогда объём получающегося тела вращения
можно вычислить по формуле
(2)
Доказательство.
Для такого тела сечение с абсциссой
– это круг радиуса
,
значити формула (1) даёт требуемый результат.
Если фигура
ограничена графиками двух непрерывных
функций
и
,
и отрезками прямыхи
,
причёми
,
то при вращении вокруг оси абсцисс
получим тело, объём которого
Пример
3. Вычислить
объём тора, полученного вращением круга,
ограниченного окружностью вокруг оси абсцисс.
Р
Указанный круг снизу ограничен графиком
функции
,
а сверху –.
Разность квадратов этих функций:
Искомый объём
(графиком
подынтегральной функции является
верхняя полуокружность, поэтому
написанный выше интеграл – это площадь
полукруга).
Пример 4.
Параболический сегмент с основанием
,
и высотой,
вращается вокруг основания. Вычислить
объём получающегося тела («лимон»
Кавальери).
Р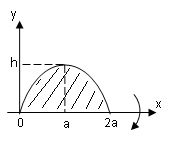
Параболу расположим как показано на
рисунке. Тогда её уравнение
,
причем.
Найдём значение параметра:
.
Итак, искомый объём:
Теорема
3. Пусть
криволинейная трапеция, ограниченная
графиком непрерывной неотрицательной
функции
,
осьюи отрезками прямых
и
,
причём,
вращается вокруг оси.
Тогда объём получающегося тела вращения
может быть найден по формуле
(3)

доказательства.
Разбиваем отрезок
точками
,
на части и проводим прямые.
Вся трапеция разложится на полоски,
которые можно считать приближенно
прямоугольниками с основаниеми высотой
.
Получающийся при
вращении такого прямоугольника цилиндр
разрежем по образующей и развернём.
Получим «почти» параллелепипед с
размерами:
,
и
.
Его объём.
Итак, для объёма тела вращения будем
иметь приближенноё равенство
Для получения
точного равенства надо перейти к пределу
при .
Написанная выше сумма есть интегральная
сумма для функции ,
следовательно, в пределе получим интеграл
из формулы (3). Теорема доказана.
Замечание
1. В теоремах
2 и 3 условие
можно опустить: формула (2) вообще
нечувствительна к знаку,
а в формуле (3) достаточнозаменить на
.
Пример
5.
Параболический сегмент (основание
,
высота)
вращается вокруг высоты. Найти объём
получающегося тела.
Расположим
параболу как показано на рисунке. И хотя
ось вращения пересекает фигуру, она –
ось – является осью симметрии. Поэтому
надо рассматривать лишь правую половину
сегмента. Уравнение параболы
,
причем,
значит.
Имеем для объёма:
Замечание
2. Если
криволинейная граница криволинейной
трапеции задана параметрическими
уравнениями
,
,
и
,
то можно использовать формулы (2) и (3) с
заменойна
и
на
при измененииt
от
до
.
Пример
6. Фигура
ограничена первой аркой циклоиды
,
,
,
и осью абсцисс. Найти объём тела,
полученного вращением этой фигуры
вокруг: 1) оси;
2) оси.
Решение.
1) Общая формула
В нашем случае:
2) Общая формула
Для нашей фигуры:
Предлагаем
студентам самостоятельно провести все
вычисления.
Замечание
3. Пусть
криволинейный сектор, ограниченный
непре-рывной линией
и лучами
,
,
вращается вокруг полярной оси. Объём
получающегося тела можно вычислить по
формуле.
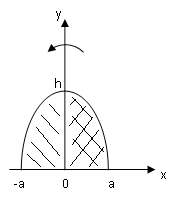
Пример
7. Часть
фигуры, ограниченной кардиоидой
,
лежащая вне окружности,
вращается вокруг полярной оси. Найти
объём тела, которое при этом получается.
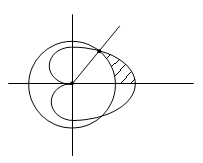
Обе линии, а значит и фигура, которую
они ограничивают, симметричны относительно
полярной оси. Поэтому необходимо
рассматривать лишь ту часть, для которой
.
Кривые пересекаются прии
при
.
Далее, фигуру можно рассматривать как
разность двух секторов, а значит и объём
вычислять как разность двух интегралов.
Имеем:
Задачи
для самостоятельного решения.
1. Круговой сегмент,
основание которого ,
высота
,
вращается вокруг основания. Найти объём
тела вращения.
2. Найти объём
параболоида вращения, основание которого
,
а высота равна.
3. Фигура, ограниченная
астроидой
,
вращает-ся вокруг оси абсцисс. Найти
объём тела, которое получается при этом.
4. Фигура, ограниченная
линиями
и
вращается вокруг оси абсцисс. Найти
объём тела вращения.
Соседние файлы в папке Лекции по мат.анализу
- #
- #
- #
- #
- #
- #
- #
Тема. «Объёмы тел вращения».
Методическое пособие по решению задач для студентов 2 курса СПО.
Дистанционная форма обучения.
1. Теоретический материал.
|
Вид круглого тела |
Формула объёма |
|
1. Цилиндр |
V = |
|
2. Конус |
V = |
|
3. Усеченный конус |
V = |
|
6. Шар |
V = |
2. Решение задач.
Задача № 1
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 36 см3.
|
Дано: Rц = Rк= R; H ц = H к= H; Vк = 36 см3 Найти: Vц
|
Решение. Vц = следовательно объем цилиндра в 3 раза больше объема конуса. Vц = 3 Vк; Vц= Ответ. 108 см3 |
Задача № 2
Высота одного цилиндра вдвое больше высоты второго цилиндра, но его радиус в два раза меньше радиуса второго цилиндра. Найти отношение их объёмов
|
Дано: R1ц = R; Н 1ц = Н; R2ц = 2R; Н 2ц = Найти: |
Решение. V1ц = V1ц =
Ответ. |
Задача № 3.
Найти объем 25м цилиндрической трубы (полого цилиндра), если внешний радиус равен 50см, диаметр стенок равен 10см.
|
|
Дано: полый цилиндр; R = 50cм = 0,5м; d = 10см = 0,1м Н = 25м Найти: V Решение. V = Ответ. 2,25 |
Задача № 4.
Объём конуса равен 36
|
Дано: конус; Н=12; V = 36 Найти: R |
Решение. Vк = 4R2=36; R2 = 36:4 = 9; R = Ответ. 3 |
Задача № 5
Объем конуса равен 24 см3. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной.
Найдите объем меньшего конуса.
|
Дано: конус Vб к = 24см3; SA = Найти: V м к |
Решение: Так как SA = Коэффициент подобия к =2, следовательно
Или: Vб к =
8 V м к = 24; V м к = 24:8=3 Ответ. 3 |
Задача № 6
Диаметр основания конуса равен 16, а длина образующей — 17. Найдите объем конуса.
|
Дано: конус, D =16; L = 17 Найти: V |
Решение: Vк =
конуса, по теореме Пифагора найдем Н. R = Н2 = L2 — R 2; Н2 = 172 = 82 =289-64=225; Н = Vк = Ответ.320 |
Задача № 7
Радиусы оснований усечённого конуса равны 4 и 12, а образующая равна 10. Вычислить объем усечённого конуса.
|
Дано: усеченный конус; R=12; r=4; l = 10. Найти: Vус.к |
Решение: V = Высоту усеченного конуса найдем из прямоугольного треугольника АВС (АВ провели параллельно h ) АВ2 = АС2 — ВС2; ВС=R-r=12-4=8 АВ2 = 102 — 82 =100-64=36; АВ=6; h=6 V = Ответ. 416 |
Задача № 8
Внутренний диаметр полого шара равен 8 см, а толщина стенок равна 2 см. Найдите объем материала, из которого сделан шар.
|
Дано: полый шар; СD = 8см; АС = 2см Найти: V Рассмотрим сечение полого шара диаметральной плоскостью. |
Решение: V=V1 — V2; V1=
r= Ответ. |
Задача № 9
Прямоугольная трапеция с основаниями 11см и 17 см и высотой 12 см вращается около прямой, проходящей через вершину острого угла перпендикулярно основаниям. Hайдите объем полученного тела вращения.
|
Дано: АВСD — трапеция; АВ=12 см. Найти: Vтела вращения |
Решение: При вращении трапеции ABCD получим цилиндр, радиус его основания R = AD =17 см, высотой Н = AB =12 см, из которого вырезан конус с радиусом основания r = CM = AD-BC r =17-11=6 см, высота h=AB=12 см. Vцил = Vкон = Vт.вр = 3468 Ответ. 3324 |
Задача № 10.
Прямоугольный треугольник с катетами 20 см и 15 см вращается вокруг гипотенузы . Найти объём полученного тела вращения.
|
Дано:
АС=15 см; ВС = 20 см. Найти: Vтела вращения |
Решение: При вращении прямоугольного треугольника АВС вокруг гипотенузы получается тело вращения, состоящее из двух конусов с общим основанием. Радиус R этого основания есть перпендикуляр СО, опущенный из вершины прямого угла на гипотенузу. Vт.вр.= V1 кон. + V2 кон; V1 кон. = Vт.вр.= По теореме Пифагора найдем гипотенузу АВ АВ2=АС2+ВС2; АВ2=152+202=225+400=625; АВ= Чтобы найти R, из треугольника АВС определим sin A. sin A= Из прямоугольного треугольника АОС sin A= Vт.вр= Ответ. 1200 |
Задания для самостоятельного решения.
1. Даны две кружки цилиндрической формы. Первая кружка в полтора раза ниже второй, а вторая вдвое шире первой. Во сколько раз объём второй кружки больше объёма первой?
2. Однородный шар диаметром 3 см имеет массу 162 грамма. Чему равна масса шара, изготовленного из того же материала, с диаметром 2 см? Ответ дайте в граммах.
3. Осевое сечение конуса равносторонний треугольник, сторона которого равна 12 см. Найдите объём конуса.
4. Найти объем тела, полученного в результате вращения прямоугольного треугольника вокруг гипотенузы, если катеты равны 3см и 4 см.
5. Прямоугольная трапеция с основанием 5 см и 8 см и высотой 4 см вращается около
большего основания. Найдите объем тела вращения.
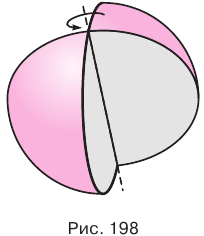
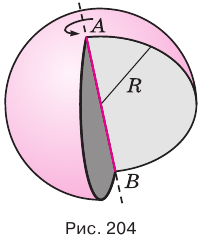
Шаром называется тело, полученное вращением круга вокруг какого-либо его диаметра (рис. 198).
Границей шара является сфера. Центр, радиус, диаметр сферы называют также центром, радиусом, диаметром шара соответственно. Расстояние от центра шара до любой его точки не больше радиуса шара.
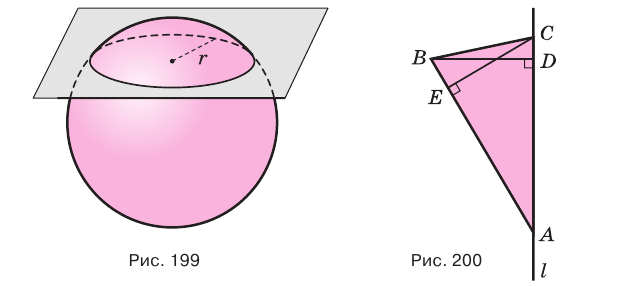
Сечением шара плоскостью является круг, радиус которого изменяется в пределах от нуля до радиуса шара (рис. 199).
Теорема 7.
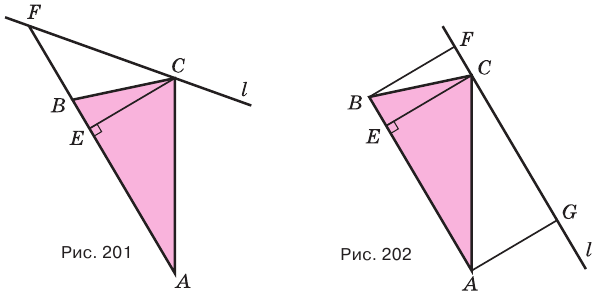
Объем тела, полученного вращением треугольника вокруг прямой, лежащей в его плоскости, проходящей через его вершину и не имеющей с треугольником общих внутренних точек, равен третьей доле произведения поверхности, образованной стороной, лежащей против той вершины треугольника, которая принадлежит оси вращения, и высоты, проведенной к этой стороне.
Доказательство:
Пусть есть тело, полученное вращением треугольника 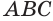

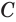

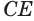
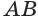
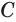
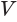
где 
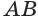
Пусть сторона 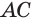

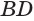
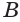

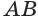
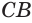
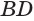
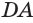
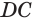
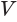
Теперь обратим внимание на то, что 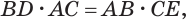
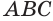
Пусть сторона 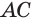

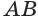
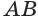

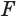
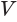
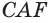
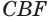
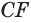
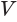
Пусть сторона 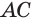

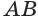
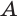
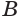
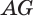
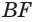

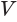
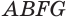
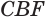
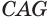
так как выражение 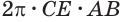
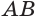
Теорема 8.
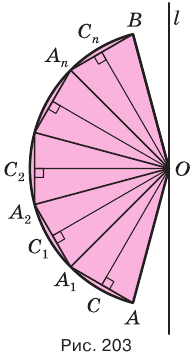
Объем тела, полученного вращением кругового сектора вокруг прямой, проходящей через его центр, лежащей в его плоскости и не имеющей с ним общих внутренних точек, равен третьей доле произведения радиуса сектора и поверхности, образованной при вращении дуги сектора.
Доказательство:
Пусть имеется тело, полученное вращением кругового сектора 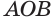
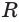

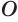
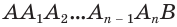

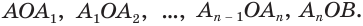
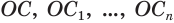
где 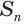
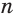
Будем увеличивать количество сторон ломаной, вписанной в круговой сектор 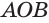
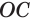
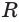
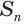
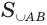
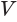
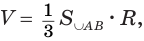

Следствие 1. Объем шара равен третьей доле произведения его поверхности и радиуса:
Действительно, шар с радиусом 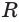
Рассмотрим комбинации шара с другими телами.
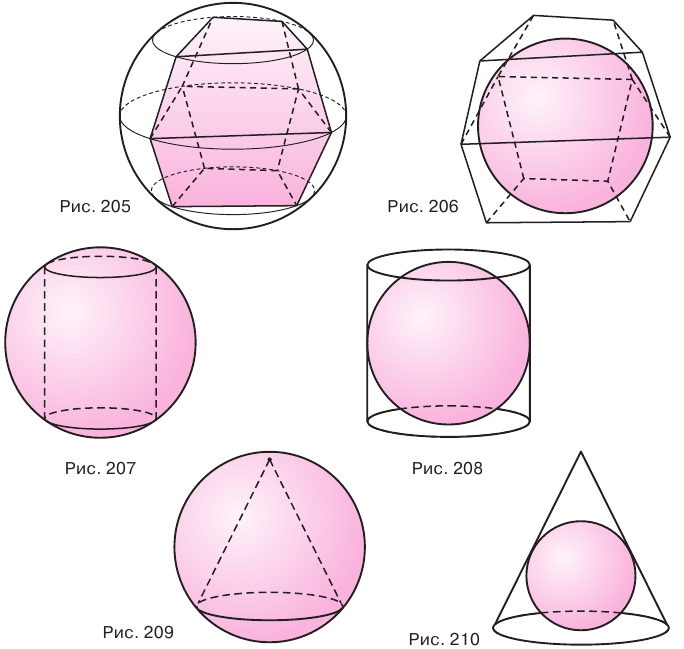
Вписанным в шар многогранником называется многогранник, все вершины которого лежат на соответствующей сфере (рис. 205). Описанным около шара многогранником называется многогранник, все грани которого касаются соответствующей сферы (рис. 206).
Вписанным в шар цилиндром называется цилиндр, окружности оснований которого принадлежат соответствующей сфере (рис. 207). Описанным около шара цилиндром называется цилиндр, основания и все образующие которого касаются соответствующей сферы (рис. 208).
Вписанным в шар конусом называется конус, вершина и окружность основания которого принадлежат соответствующей сфере (рис. 209). Описанным около шара конусом называется конус, основание и все образующие которого касаются соответствующей сферы (рис. 210).
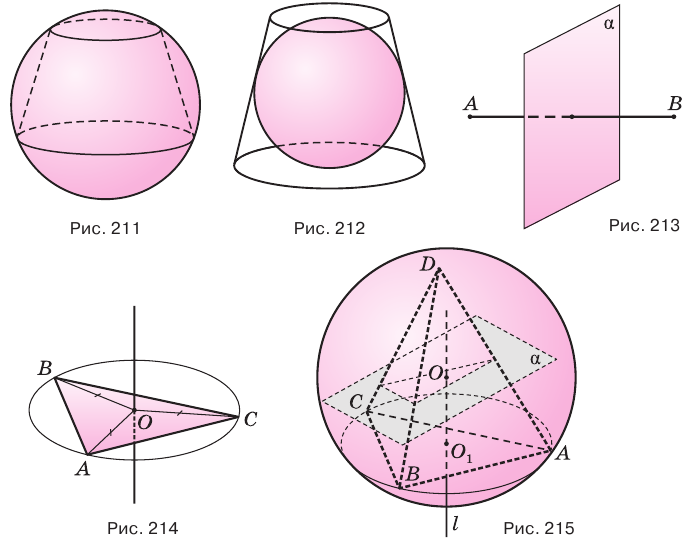
Вписанным в шар усеченным конусом называется усеченный конус, окружности оснований которого принадлежат соответствующей сфере (рис. 211). Описанным около шара усеченным конусом называется конус, основания и все образующие которого касаются соответствующей сферы (рис. 212).
Теорема 9.
Около каждой треугольной пирамиды можно описать единственный шар.
Доказательство:
Сначала обратим внимание на то, что геометрическое место точек, равноудаленных от кондов отрезка, есть плоскость, проходящая через середину отрезка и перпендикулярная ему (рис. 213). Она называется серединной плоскостью отрезка. Геометрическим местом точек, равноудаленных от вершин треугольника, является прямая, проходящая через центр описанной около треугольника окружности и перпендикулярная его плоскости (рис. 214).
Пусть есть треугольная пирамида 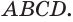
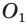
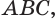


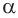



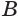
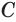

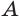
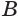
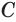
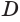

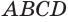


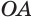
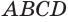
Единственность найденного шара следует из того, что прямая 

Следствие 2. Четыре точки пространства, не лежащие в одной плоскости, определяют единственную сферу, единственный шар.
Теорема 10.
В каждую треугольную пирамиду можно вписать единственный шар.
Доказательство:
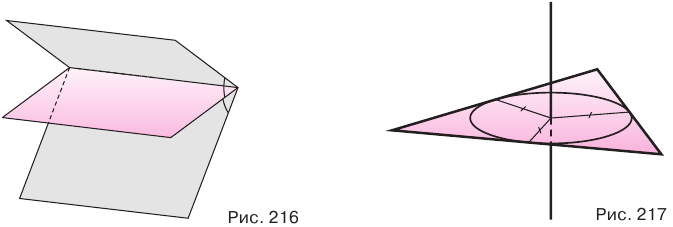
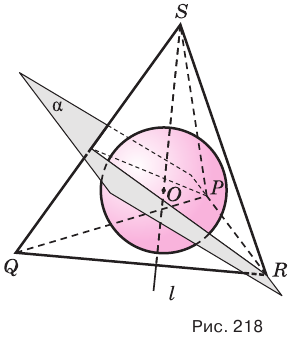
Сначала обратим внимание на то, что геометрическим местом точек, равноудаленных от граней двугранного угла, является полуплоскость, граница которой совпадает с ребром двугранного угла и которая делит этот угол пополам (рис. 216). Она называется биссекторной плоскостью угла. Геометрическим местом точек, равноудаленных от сторон треугольника, является прямая, проходящая через центр вписанной в треугольник окружности и перпендикулярная его плоскости (рис. 217).
Пусть есть треугольная пирамида 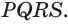
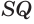
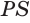


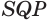
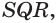
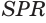
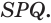

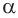
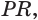


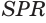
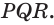


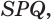
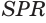
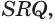
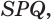
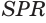
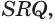
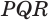

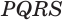


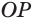
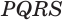
Единственность найденного шара следует из того, что прямая 

Теорема 11.
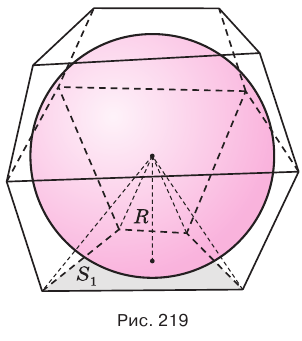
Объем описанного около шара многогранника равен третьей доле произведения полной поверхности многогранника и радиуса шара.
Доказательство:
Пусть есть многогранник, который описан около шара (рис. 219). Центр шара соединим со всеми вершинами многогранника. Если многогранник имеет 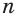
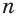
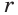
Пусть площади граней многогранника равны 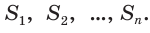
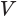
где 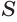
- Правильные многогранники в геометрии
- Многогранники
- Окружность
- Эллипс
- Цилиндр в геометрии
- Пирамида в геометрии
- Конус в геометрии
- Сфера в геометрии