Определение
1.
Квадратная матрица
называется невырожденной
( или неособенной), если
,
в противном случае матрица называется
вырожденной
( особенной ).
Определение
2.
Пусть задана квадратная матрица А, то
матрица
называется взаимной
к
матрице
,
если в ее к-ой строке стоят алгебраические
дополнения элементов k-
го столбца матрицы А, т.е.

Теорема
1.
Для взаимной матрицы
квадратной матрицы А выполнено равенство
А=
А
= АI
= АI
=
где
— определитель матрицы А.
Доказательство.
Докажем для случая А
= АI
=
I
А=

I
Теорема
2.
Особенные матрицы обратных матриц не
имеют. Всякая неособенная матрица имеет
обратную
и причем единственную, определяемую по
формуле
Доказательство.
По определению обратной Х матрицы А А-1
= А-1
А = I
и свойству, что определитель произведение
равен произведению определителей,
получаем
А
А-1
=
А-1
А =
I=
1
0
т.е.
определители матрицы А и А-1
не равны нулю.
Используем
теорему 1: если А
=
I,
то умножая слева на А-1
получим
А-1А
= А-1
I
или
= А-1
и окончательно будет
Докажем
единственность.
Пусть существуют 2 обратные матрицы Y1,
Y.
Тогда А Y
= I,
Y1
(А
Y)
= Y1I,
(Y1
А)Y
= Y1
, I
Y
= Y1,
Y
= Y1
Следствие
1..
Свойство вытекает из цепочки равенств
2.
Замечание:.
Показать,
что если матрица А симметрическая
(кососимметричная), то взаимная матрица
Аж
также
симметрическая (кососимметричная).
Пример.
Найти обратную
матрицу
для матрицы
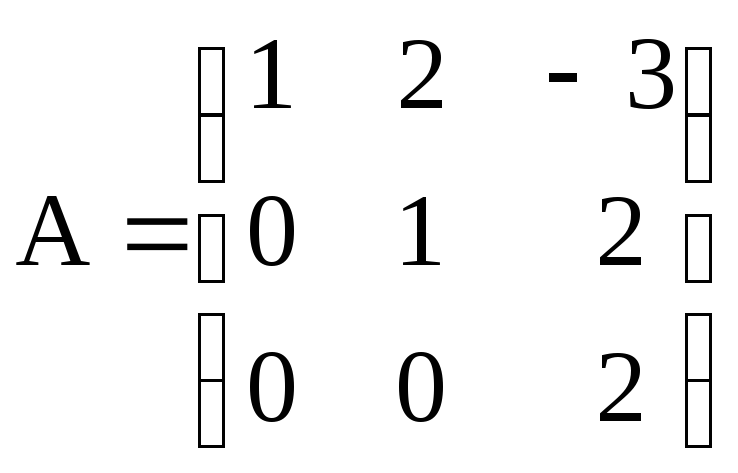
Так
как
,
то обратная матрица существует. Для
удобства вычисления запишем
транспонированную с ней матрицу
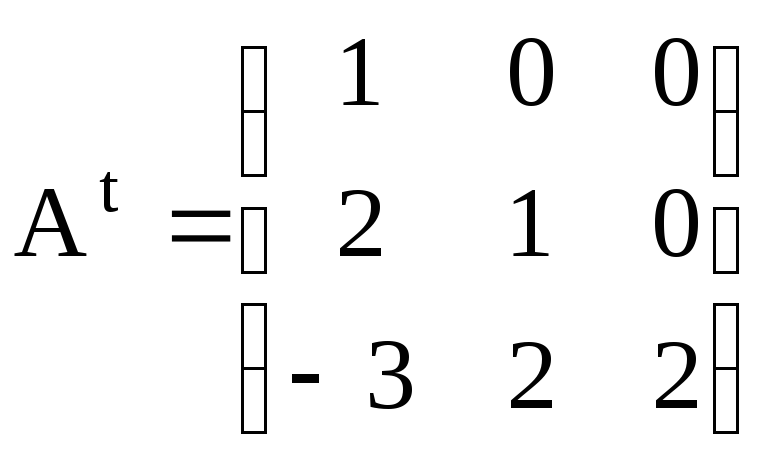
и найдем ее алгебраические дополнения
А11
= 2, А12
= 0, А13
= 0,
А21
=-4, А22
= 2, А23
= 0,
А31
= 7, А32
= -2, А33
= 1
Взаимная
матрица

обратная

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы.
Матрица $A^{-1}$ называется обратной по отношению к квадратной матрице $A$, если выполнено условие $A^{-1}cdot A=Acdot A^{-1}=E$, где $E$ – единичная матрица, порядок которой равен порядку матрицы $A$.
Невырожденная матрица – матрица, определитель которой не равен нулю. Соответственно, вырожденная матрица – та, у которой равен нулю определитель.
Обратная матрица $A^{-1}$ существует тогда и только тогда, когда матрица $A$ – невырожденная. Если обратная матрица $A^{-1}$ существует, то она единственная.
Есть несколько способов нахождения обратной матрицы, и мы рассмотрим два из них. На этой странице будет рассмотрен метод присоединённой матрицы, который полагается стандартным в большинстве курсов высшей математики. Второй способ нахождения обратной матрицы (метод элементарных преобразований), который предполагает использование метода Гаусса или метода Гаусса-Жордана, рассмотрен во второй части.
Метод присоединённой (союзной) матрицы
Пусть задана матрица $A_{ntimes n}$. Для того, чтобы найти обратную матрицу $A^{-1}$, требуется осуществить три шага:
- Найти определитель матрицы $A$ и убедиться, что $Delta Aneq 0$, т.е. что матрица А – невырожденная.
- Составить алгебраические дополнения $A_{ij}$ каждого элемента матрицы $A$ и записать матрицу $A_{ntimes n}^{*}=left(A_{ij} right)$ из найденных алгебраических дополнений.
- Записать обратную матрицу с учетом формулы $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$.
Матрицу ${A^{*}}^T$ часто именуют присоединённой (взаимной, союзной) к матрице $A$.
Если решение происходит вручную, то первый способ хорош лишь для матриц сравнительно небольших порядков: второго (пример №2), третьего (пример №3), четвертого (пример №4). Чтобы найти обратную матрицу для матрицы высшего порядка, используются иные методы. Например, метод Гаусса, который рассмотрен во второй части.
Пример №1
Найти матрицу, обратную к матрице $A=left( begin{array} {cccc} 5 & -4 &1 & 0 \ 12 &-11 &4 & 0 \ -5 & 58 &4 & 0 \ 3 & -1 & -9 & 0 end{array} right)$.
Решение
Так как все элементы четвёртого столбца равны нулю, то $Delta A=0$ (т.е. матрица $A$ является вырожденной). Так как $Delta A=0$, то обратной матрицы к матрице $A$ не существует.
Ответ: матрицы $A^{-1}$ не существует.
Пример №2
Найти матрицу, обратную к матрице $A=left(begin{array} {cc} -5 & 7 \ 9 & 8 end{array}right)$. Выполнить проверку.
Решение
Используем метод присоединённой матрицы. Сначала найдем определитель заданной матрицы $A$:
$$
Delta A=left| begin{array} {cc} -5 & 7\ 9 & 8 end{array}right|=-5cdot 8-7cdot 9=-103.
$$
Так как $Delta A neq 0$, то обратная матрица существует, посему продолжим решение. Находим алгебраические дополнения каждого элемента заданной матрицы:
begin{aligned}
& A_{11}=(-1)^2cdot 8=8; ; A_{12}=(-1)^3cdot 9=-9;\
& A_{21}=(-1)^3cdot 7=-7; ; A_{22}=(-1)^4cdot (-5)=-5.\
end{aligned}
Составляем матрицу из алгебраических дополнений: $A^{*}=left( begin{array} {cc} 8 & -9\ -7 & -5 end{array}right)$.
Транспонируем полученную матрицу: ${A^{*}}^T=left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)$ (полученная матрица часто именуется присоединённой или союзной матрицей к матрице $A$).
Используя формулу $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$, имеем:
$$
A^{-1}=frac{1}{-103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)
=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)
$$
Итак, обратная матрица найдена:
$$A^{-1}=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right).$$
Чтобы проверить истинность результата, достаточно проверить истинность одного из равенств: $A^{-1}cdot A=E$ или $Acdot A^{-1}=E$. Проверим выполнение равенства $A^{-1}cdot A=E$. Дабы поменьше работать с дробями, будем подставлять матрицу $A^{-1}$ не в форме $left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)$, а в виде $-frac{1}{103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)$:
$$
A^{-1}cdot{A}
=-frac{1}{103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)cdotleft(begin{array} {cc} -5 & 7 \ 9 & 8 end{array}right)
=-frac{1}{103}cdotleft(begin{array} {cc} -103 & 0 \ 0 & -103 end{array}right)
=left(begin{array} {cc} 1 & 0 \ 0 & 1 end{array}right)
=E
$$
Проверка пройдена успешно, обратная матрица $A^{-1}$ найдена верно.
Ответ: $A^{-1}=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)$.
Пример №3
Найти обратную матрицу для матрицы $A=left( begin{array} {ccc} 1 & 7 & 3 \ -4 & 9 & 4 \ 0 & 3 & 2end{array} right)$. Выполнить проверку.
Решение
Начнём с вычисления определителя матрицы $A$. Итак, определитель матрицы $A$ таков:
$$
Delta A=left| begin{array} {ccc} 1 & 7 & 3 \ -4 & 9 & 4 \ 0 & 3 & 2end{array} right| = 18-36+56-12=26.
$$
Так как $Delta Aneq 0$, то обратная матрица существует, посему продолжим решение. Находим алгебраические дополнения каждого элемента заданной матрицы:
$$
begin{aligned}
& A_{11}=(-1)^{2}cdotleft|begin{array}{cc} 9 & 4\ 3 & 2end{array}right|=6;;
A_{12}=(-1)^{3}cdotleft|begin{array}{cc} -4 &4 \ 0 & 2end{array}right|=8;;
A_{13}=(-1)^{4}cdotleft|begin{array}{cc} -4 & 9\ 0 & 3end{array}right|=-12;\
& A_{21}=(-1)^{3}cdotleft|begin{array}{cc} 7 & 3\ 3 & 2end{array}right|=-5;;
A_{22}=(-1)^{4}cdotleft|begin{array}{cc} 1 & 3\ 0 & 2end{array}right|=2;;
A_{23}=(-1)^{5}cdotleft|begin{array}{cc} 1 & 7\ 0 & 3end{array}right|=-3;\
& A_{31}=(-1)^{4}cdotleft|begin{array}{cc} 7 & 3\ 9 & 4end{array}right|=1;;
A_{32}=(-1)^{5}cdotleft|begin{array}{cc} 1 & 3\ -4 & 4end{array}right|=-16;;
A_{33}=(-1)^{6}cdotleft|begin{array}{cc} 1 & 7\ -4 & 9end{array}right|=37.
end{aligned}
$$
Составляем матрицу из алгебраических дополнений и транспонируем её:
$$
A^*=left( begin{array} {ccc} 6 & 8 & -12 \ -5 & 2 & -3 \ 1 & -16 & 37end{array} right); ;
{A^*}^T=left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right).
$$
Используя формулу $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$, получим:
$$
A^{-1}=frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)=
left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)
$$
Чтобы проверить истинность результата, достаточно проверить истинность одного из равенств: $A^{-1}cdot A=E$ или $Acdot A^{-1}=E$. Проверим выполнение равенства $Acdot A^{-1}=E$. Дабы поменьше работать с дробями, будем подставлять матрицу $A^{-1}$ не в форме $left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)$, а в виде $frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)$:
$$
Acdot{A^{-1}}
=left( begin{array}{ccc}
1 & 7 & 3 \
-4 & 9 & 4\
0 & 3 & 2end{array} right)cdot
frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)
=frac{1}{26}cdotleft( begin{array} {ccc} 26 & 0 & 0 \ 0 & 26 & 0 \ 0 & 0 & 26end{array} right)
=left( begin{array} {ccc} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1end{array} right)
=E
$$
Проверка пройдена успешно, обратная матрица $A^{-1}$ найдена верно.
Ответ: $A^{-1}=left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)$.
Пример №4
Найти матрицу, обратную матрице $A=left( begin{array} {cccc} 6 & -5 & 8 & 4\ 9 & 7 & 5 & 2 \ 7 & 5 & 3 & 7\ -4 & 8 & -8 & -3 end{array} right)$.
Решение
Для матрицы четвёртого порядка нахождение обратной матрицы с помощью алгебраических дополнений несколько затруднительно. Однако такие примеры в контрольных работах встречаются.
Чтобы найти обратную матрицу, для начала нужно вычислить определитель матрицы $A$. Лучше всего в данной ситуации это сделать с помощью разложения определителя по строке (столбцу). Выбираем любую строку или столбец и находим алгебраические дополнения каждого элемента избранной строки или столбца.
Например, для первой строки получим:
$$
A_{11}=left|begin{array}{ccc} 7 & 5 & 2\ 5 & 3 & 7\ 8 & -8 & -3 end{array}right|=556;;
A_{12}=-left|begin{array}{ccc} 9 & 5 & 2\ 7 & 3 & 7 \ -4 & -8 & -3 end{array}right|=-300;
$$
$$
A_{13}=left|begin{array}{ccc} 9 & 7 & 2\ 7 & 5 & 7\ -4 & 8 & -3 end{array}right|=-536;;
A_{14}=-left|begin{array}{ccc} 9 & 7 & 5\ 7 & 5 & 3\ -4 & 8 & -8 end{array}right|=-112.
$$
Определитель матрицы $A$ вычислим по следующей формуле:
$$
Delta{A}=a_{11}cdot A_{11}+a_{12}cdot A_{12}+a_{13}cdot A_{13}+a_{14}cdot A_{14}=6cdot 556+(-5)cdot(-300)+8cdot(-536)+4cdot(-112)=100.
$$
А далее продолжаем находить алгебраические дополнения:
$$
begin{aligned}
& A_{21}=-77;;A_{22}=50;;A_{23}=87;;A_{24}=4;\
& A_{31}=-93;;A_{32}=50;;A_{33}=83;;A_{34}=36;\
& A_{41}=473;;A_{42}=-250;;A_{43}=-463;;A_{44}=-96.
end{aligned}
$$
Матрица из алгебраических дополнений:
$$A^*=left(begin{array}{cccc} 556 & -300 & -536 & -112\ -77 & 50 & 87 & 4 \ -93 & 50 & 83 & 36\ 473 & -250 & -463 & -96end{array}right)$$
Присоединённая матрица:
$${A^*}^T=left(begin{array} {cccc} 556 & -77 & -93 & 473\ -300 & 50 & 50 & -250 \ -536 & 87 & 83 & -463\ -112 & 4 & 36 & -96end{array}right)$$
Обратная матрица:
$$
A^{-1}=frac{1}{100}cdot left( begin{array} {cccc} 556 & -77 & -93 & 473\ -300 & 50 & 50 & -250 \ -536 & 87 & 83 & -463\ -112 & 4 & 36 & -96 end{array} right)=
left( begin{array} {cccc} 139/25 & -77/100 & -93/100 & 473/100 \ -3 & 1/2 & 1/2 & -5/2 \ -134/25 & 87/100 & 83/100 & -463/100 \ -28/25 & 1/25 & 9/25 & -24/25 end{array} right)
$$
Проверка, при желании, может быть произведена так же, как и в предыдущих примерах.
Ответ: $A^{-1}=left( begin{array} {cccc} 139/25 & -77/100 & -93/100 & 473/100 \ -3 & 1/2 & 1/2 & -5/2 \ -134/25 & 87/100 & 83/100 & -463/100 \ -28/25 & 1/25 & 9/25 & -24/25 end{array} right)$.
Во второй части будет рассмотрен иной способ нахождения обратной матрицы, который предполагает использование преобразований метода Гаусса или метода Гаусса-Жордана.
Как найти присоединенную матрицу
Найти присоединенную матрицу можно только для квадратной исходной матрицы, поскольку метод расчета подразумевает предварительное транспонирование. Это одна из операций в матричной алгебре, итогом которой является замена столбцов соответствующими строками. Кроме того, необходимо определить алгебраические дополнения.

Инструкция
Основой матричной алгебры являются операции над матрицами и поиск их основных характеристик. Чтобы найти присоединенную матрицу необходимо выполнить транспонирование и сформировать на основе ее результата новую матрицу из соответствующих алгебраических дополнений.
Транспонирование квадратной матрицы – это запись ее элементов в другом порядке. Первый столбец меняется на первую строку, второй – на вторую и т.д. в общем виде это выглядит так (см. рисунок).
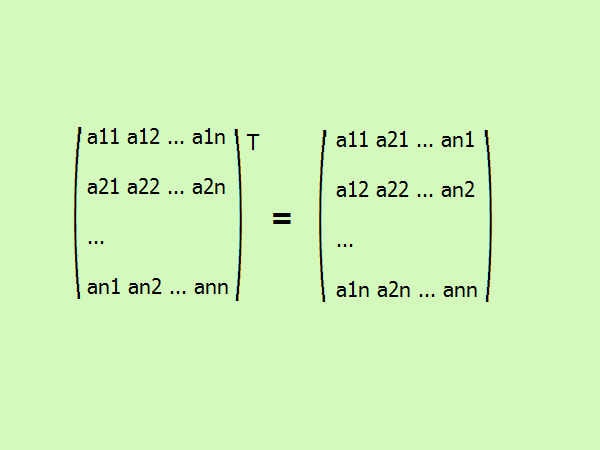
Второй этап нахождения присоединенной матрицы – поиск алгебраических дополнений. Эти числовые характеристики матричных элементов получаются путем вычисления миноров. Те, в свою очередь, являются определителями исходной матрицы порядка, меньшего на 1, и получаются вычеркиванием соответствующих строк и столбцов. Например, M11 = (a22•a33 – a23•a32). Алгебраическое дополнение отличается от минора коэффициентом, равным (-1) в степени суммы номеров элемента: A11 = (-1)^(1+1)• (a22•a33 – a23•a32).
Рассмотрите пример: найдите присоединенную матрицу к данной. Для удобства возьмем третий порядок. Это позволит быстрее понять алгоритм, не прибегая к тяжелым вычислениям, ведь для расчета определителей матрицы третьего порядка достаточно всего четырех элементов.
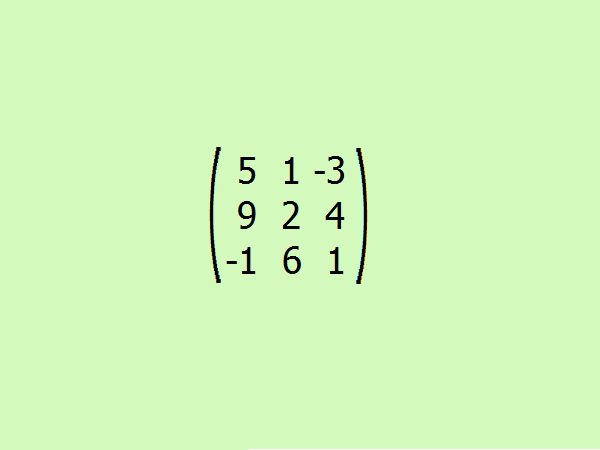
Проведите транспонирование заданной матрицы. Здесь требуется поменять местами первую строку на первый столбец, вторую – на второй и третью – на третий.
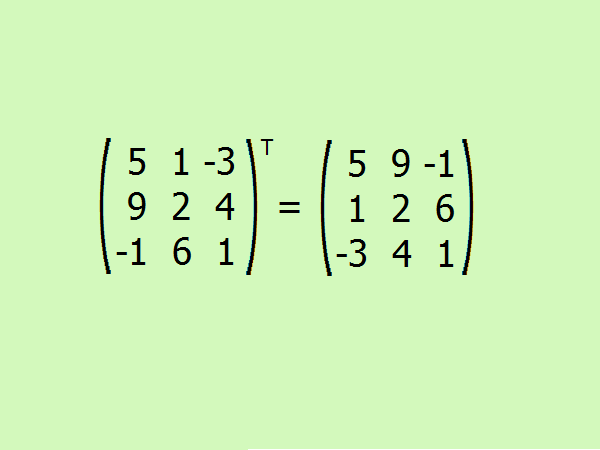
Запишите выражения для поиска алгебраических дополнений, всего их будет 9 по количеству элементов матрицы. Будьте внимательны со знаком, лучше воздержаться от расчетов в уме и расписать все подробно.
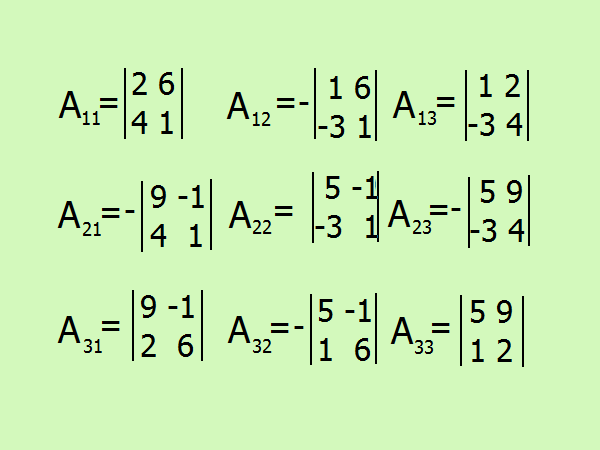
A11 = (-1)²•(2 -24) = -22;
A12 = (-1)³•(1+ 18) = -19;
A13 = (-1)^4•(4 + 6) = 10;
A21 = (-1)³•(9 + 4) = -13;
A22 = (-1)^4•(5 — 3) = 2;
A23 = (-1)^5•(20 + 27);
A31 = (-1)^4•(54 + 2) = 56;
A32 = (-1)^5•(30 + 1) = -31;
A33 = (-1)^6•(10 — 9) = 1.
Составьте итоговую присоединенную матрицу из получившихся алгебраических дополнений.
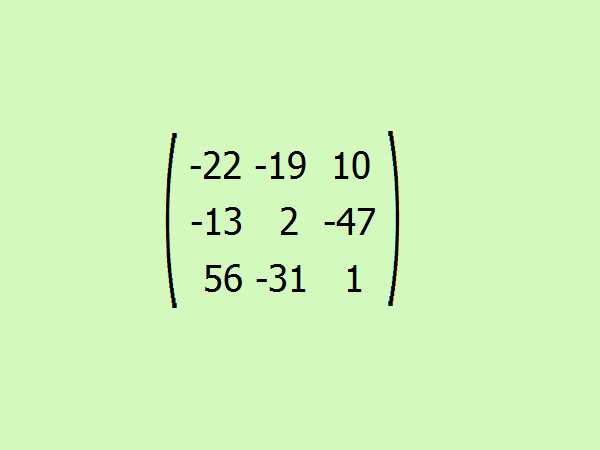
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Взаимно обратные матрицы примеры. Нахождение обратной матрицы онлайн
Нахождение обратной матрицы
— задача, которая чаще решается двумя методами:
- методом алгебраических дополнений, при котором требуется находить определители и транспонировать матрицы;
- методом исключения неизвестных Гаусса, при котором требуется производить элементарные преобразования матриц
(складывать строки, умножать строки на одно и то же число и т. д.).
Для особо любознательных существуют и другие методы, например, метод линейных
преобразований. На этом уроке разберём три упомянутых метода и алгоритмы нахождения обратной матрицы
этими методами.
Обратной матрицей
А
, называется такая матрица
А
. (1)
Обратной матрицей
, которую требуется отыскать для данной квадратной матрицы А
, называется такая матрица
произведение на которую матрицы А
справа является единичной матрицей, т. е,
. (1)
Единичной матрицей называется диагональная матрица, у которой все диагональные
элементы равны единице.
Теорема.
Для каждой неособенной (невырожденной, несингулярной) квадратной матрицы можно найти обратную матрицу, и притом только одну. Для особенной (вырожденной, сингулярной) квадратной матрицы обратная матрица не существует.
Квадратная матрица называется неособенной
(или невырожденной
, несингулярной
), если её определитель не равен нулю, и особенной
(или вырожденной
, сингулярной
), если её определитель равен нулю.
Обратная матрица может быть найдена только для квадратной матрицы. Естественно,
обратная матрица также будет квадратной и того же порядка, что и данная матрица. Матрица, для которой
может быть найдена обратная матрица, называется обратимой матрицей.
Для обратной матрицы
существует уместная аналогия с обратным
числом. Для каждого числа a
, не равного нулю, существует такое число
b
, что произведение
a
и b
равно единице: ab
= 1
.
b
называется обратным для числа b
. Например, для числа 7 обратным является число 1/7,
так как 7*1/7=1.
Нахождение обратной матрицы методом алгебраических дополнений (союзной матрицы)
Для неособенной квадратной матрицы А
обратной является матрица
где —
определитель матрицы А
, а
— матрица, союзная с матрицей А
.
Союзной с квадратной матрицей A
называется матрица
того же порядка, элементами которой являются алгебраические дополнения соответствующих элементов определителя матрицы
,
транспонированной относительно матрицы A. Таким образом, если
то
и
Алгоритм нахождения обратной матрицы методом алгебраических дополнений
1. Найти определитель данной матрицы A
. Если определитель равен нулю, нахождение
обратной матрицы прекращается, так как матрица вырожденная и обратная для неё не существует.
2. Найти матрицу, транспонированную относительно A
.
3. Вычислить элементы союзной матрицы как алгебраические дополнения марицы, найденной на шаге 2.
4. Применить формулу (2): умножить число, обратное определителю матрицы A
,
на союзную матрицу, найденную на шаге 4.
5. Проверить полученный на шаге 4 результат, умножив данную матрицу A
на
обратную матрицу. Если произведение этих матриц равно единичной матрицы, значит обратная матрица была
найдена верно. В противном случае начать процесс решения снова.
Пример 1.
Для матрицы
найти обратную матрицу.
Решение. Для нахождения обратной матрицы необходимо найти определитель матрицы А
.
Находим по правилу треугольников:
Следовательно, матрица А
– неособенная (невырожденная, несингулярная) и для неё существует обратная.
Найдём матрицу, союзную с данной матрицей А
.
Найдём матрицу
,
транспонированную относительно матрицы A
:
Вычисляем элементы союзной матрицы как алгебраические дополнения матрицы,
транспонированной относительно матрицы A
:
Следовательно, матрица
,
союзная с матрицей A
, имеет вид
Замечание.
Порядок вычисления элементов и транспонирования матрицы может
быть иным. Можно сначала вычислить алгебраические дополнения матрицы A
, а затем транспонировать
матрицу алгебраических дополнений. В результате должны получиться те же элементы союзной матрицы.
Применяя формулу (2), находим матрицу, обратную матрице А
:
Нахождение обратной матрицы методом исключения неизвестных Гаусса
Первый шаг для нахождения обратной матрицы методом исключения неизвестных Гаусса —
приписать к матрице
A
единичную матрицу того же порядка, отделив их вертикальной чертой. Мы
получим сдвоенную матрицу .
Умножим обе части этой матрицы на ,
тогда получим
,
Алгоритм нахождения обратной матрицы методом исключения неизвестных Гаусса
1. К матрице A
приписать единичную матрицу того же порядка.
2. Полученную сдвоенную матрицу преобразовать так, чтобы в левой её части получилась
единичная матрица, тогда в правой части на месте
единичной матрицы автоматически получится обратная матрица.
в левой части
преобразуется в единичную матрицу путём элементарных преобразований матрицы.
2. Если в процессе преобразования матрицы A
в единичную матрицу в какой-либо
строке или в каком-либо столбце окажутся только нули, то определитель матрицы равен
нулю, и, следовательно, матрица
A
будет вырожденной, и она не имеет обратной матрицы. В этом
случае дальнейшее нахождение обратной матрицы прекращается.
Пример 2.
Для матрицы
найти обратную матрицу.
и будем её преобразовывать, так чтобы в левой части получилась единичная матрица.
Начинаем преобразования.
Умножим первую строку левой и правой матрицы на (-3) и сложим её со второй строкой,
а затем умножим первую строку на (-4) и сложим её с третьей строкой, тогда получим
.
Чтобы по возможности не было дробных чисел при последующих преобразованиях, создадим
предварительно единицу во второй строке в левой части сдвоенной матрицы. Для этого умножим вторую строку
на 2 и вычтем из неё третью строку, тогда получим
.
Сложим первую строку со второй, а затем умножим вторую строку на (-9) и сложим её
с третьей строкой. Тогда получим
.
Разделим третью строку на 8, тогда
.
Умножим третью строку на 2 и сложим её со второй строкой. Получается:
.
Переставим местами вторую и третью строку, тогда окончательно получим:
.
Видим, что в левой части получилась единичная матрица, следовательно, в правой части
получилась обратная матрица .
Таким образом:
.
Можно проверить правильность вычислений, умножим исходную матрицу на найденную обратную матрицу:
В результате должна получиться обратная матрица.
Пример 3.
Для матрицы
найти обратную матрицу.
Решение. Составляем сдвоенную матрицу
и будем её преобразовывать.
Первую строку умножаем на 3, а вторую на 2, и вычитаем из второй,
а затем первую строку умножаем на 5, а третью на 2 и вычитаем из третьей строки, тогда получим
.
Первую строку умножаем на 2 и складываем её со второй, а затем из третьей строки
вычитаем вторую, тогда получим
.
Видим, что в третьей строке в левой части все элементы получились равными нулю.
Следовательно, матрица вырожденная и обратной матрицы не имеет. Дальнейшее нахождение обратной марицы прекращаем.
Матричная алгебра — Обратная матрица
Обратная матрица
Обратной матрицей
называется матрица, которая при умножении как справа, так и слева на данную матрицу дает единичную матрицу.
Обозначим обратную матрицу к матрице А
через , тогда согласно определению получим:
где Е
– единичная матрица.
Квадратная матрица
называется неособенной
(невырожденной
), если ее определитель не равен нулю. В противном случае она называется особенной
(вырожденной
) или сингулярной
.
Имеет место теорема: всякая неособенная матрица имеет обратную матрицу.
Операция нахождения обратной матрицы называется обращением
матрицы. Рассмотрим алгоритм обращения матрицы.
-го порядка:
где Δ = det A
≠ 0.
Алгебраическим дополнением элемента
матрицы n
-го порядка А
называется взятый с определенным знаком определитель матрицы (n
–1)-го порядка, полученной вычеркиванием i
-ой строки и j
-го столбца матрицы А
:
Составим так называемую присоединенную
матрицу:
где– алгебраические дополнения соответствующих элементовматрицы А
.
Заметим, что алгебраические дополнения элементов строк матрицы А
размещаются в соответствующих столбцах матрицы Ã
, то есть одновременно производится транспонирование матрицы.
Разделив все элементы матрицы
Ã
на Δ – величину определителя матрицы А
, получим в результате обратную матрицу:
Отметим ряд особых свойств обратной матрицы:
1) для данной матрицы А
ее обратная матрица
является единственной;
2) если существует обратная матрица , то правая обратная
и левая обратная
матрицы совпадают с ней;
3) особенная (вырожденная) квадратная матрица не имеет обратной матрицы.
Основные свойства обратной матрицы:
1) определитель обратной матрицы и определитель исходной матрицы являются обратными величинами;
2) обратная матрица произведения квадратных матриц равна произведениюобратных матриц сомножителей, взятому в обратном порядке:
3) транспонированная обратная матрица равна обратной матрице от данной транспонированной матрицы:
П р и м е р. Вычислить матрицу, обратную данной.
Как правило, обратные операции используются для упрощения сложных алгебраических выражений. Например, если в задаче присутствует операция деления на дробь, можно заменить ее операцией умножения на обратную дробь, что является обратной операцией. Более того, матрицы делить нельзя, поэтому нужно умножать на обратную матрицу. Вычислять матрицу, обратную матрице размером 3х3, довольно утомительно, но нужно уметь делать это вручную. Также обратную величину можно найти с помощью хорошего графического калькулятора.
Шаги
С помощью присоединенной матрицы
Транспонируйте исходную матрицу.
Транспонирование – это замена строк на столбцы относительно главной диагонали матрицы, то есть нужно поменять местами элементы (i,j) и (j,i). При этом элементы главной диагонали (начинается в верхнем левом углу и заканчивается в нижнем правом углу) не меняются.
- Чтобы поменять строки на столбцы, запишите элементы первой строки в первом столбце, элементы второй строки во втором столбце, а элементы третьей строки в третьем столбце. Порядок изменения положения элементов показан на рисунке, на котором соответствующие элементы обведены цветными кружками.
Найдите определить каждой матрицы размером 2х2.
Каждый элемент любой матрицы, включая транспонированную, связан с соответствующей матрицей 2х2. Чтобы найти матрицу 2х2, которая соответствует определенному элементу, зачеркните строку и столбец, в которых находится данный элемент, то есть нужно зачеркнуть пять элементов исходной матрицы 3х3. Незачеркнутыми останутся четыре элемента, которые являются элементами соответствующей матрицы 2х2.
- Например, чтобы найти матрицу 2х2 для элемента, который расположен на пересечении второй строки и первого столбца, зачеркните пять элементов, которые находятся во второй строке и первом столбце. Оставшиеся четыре элемента являются элементами соответствующей матрицы 2х2.
- Найдите определитель каждой матрицы 2х2. Для этого произведение элементов второстепенной диагонали вычтите из произведения элементов главной диагонали (смотрите рисунок).
- Подробную информацию о матрицах 2х2, соответствующих определенным элементам матрицы 3х3, можно найти в интернете.
Создайте матрицу кофакторов.
Результаты, полученные ранее, запишите в виде новой матрицы кофакторов. Для этого найденный определитель каждой матрицы 2х2 напишите там, где располагался соответствующий элемент матрицы 3х3. Например, если рассматривается матрица 2х2 для элемента (1,1), ее определитель запишите в позиции (1,1). Затем поменяйте знаки соответствующих элементов согласно определенной схеме, которая показана на рисунке.
- Схема изменения знаков: знак первого элемента первой строки не меняется; знак второго элемента первой строки меняется на противоположный; знак третьего элемента первой строки не меняется и так далее построчно. Обратите внимание, что знаки «+» и «-», которые показаны на схеме (смотрите рисунок), не свидетельствуют о том, что соответствующий элемент будет положительным или отрицательным. В данном случае знак «+» говорит о том, что знак элемента не меняется, а знак «-» свидетельствует об изменении знака элемента.
- Подробную информацию о матрицах кофакторов можно найти в интернете.
- Так вы найдете присоединенную матрицу исходной матрицы. Иногда ее называют комплексно-сопряженной матрицей. Такая матрица обозначается как adj(M).
Разделите каждый элемент присоединенной матрицы на определитель.
Определитель матрицы М был вычислен в самом начале, чтобы проверить, что обратная матрица существует. Теперь разделите каждый элемент присоединенной матрицы на этот определитель.
- Определитель матрицы, которая показана на рисунке, равен 1. Таким образом, здесь присоединенная матрица является обратной матрицей (потому что при делении любого числа на 1 оно не меняется).
- В некоторых источниках операция деления заменяется операцией умножения на 1/det(М). При этом конечный результат не меняется.
Запишите обратную матрицу.
Запишите элементы, расположенные на правой половине большой матрицы, в виде отдельной матрицы, которая является обратной матрицей.
Введите исходную матрицу в память калькулятора.
Для этого нажмите кнопку Matrix (Матрица), если она есть. В случае калькулятора Texas Instruments, возможно, понадобится нажать кнопки 2 nd и Matrix.
Выберите меню Edit (Редактирование).
Сделайте это с помощью кнопок со стрелками или соответствующей функциональной кнопки, которая находится в верхней части клавиатуры калькулятора (расположение кнопки зависит от модели калькулятора).
- Смена мест двух строк.
- Умножение всех элементов строки на некоторое число, не равное нулю.
- Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на любой множитель.
Применять указанные элементарные преобразования можно разными путями. Обычно выбирают метод Гаусса или метод Гаусса-Жордана. Вообще, методы Гаусса и Гаусса-Жордана предназначены для решения систем линейных алгебраических уравнений, а не для нахождения обратных матриц. Фразу «применение метода Гаусса для нахождения обратной матрицы» здесь нужно понимать как «применение операций, свойственных методу Гаусса, для нахождения обратной матрицы».
Нумерация примеров продолжена с первой части . В примерах и рассмотрено применение метода Гаусса для нахождения обратной матрицы, а в примерах и разобрано использование метода Гаусса-Жордана. Следует отметить, что если в ходе решения все элементы некоторой строки или столбца матрицы, расположенной до черты, обнулились, то обратной матрицы не существует.
Теперь приступим к решению. Метод Гаусса делится на два этапа: прямой ход и обратный (подробное описание этого метода для решения систем уравнений дано в примерах соответствующей темы). Те же два этапа будут применены и в процессе отыскания обратной матрицы.
Прямой ход
Первый шаг
С помощью первой строки обнуляем элементы первого столбца, расположенные под первой строкой:
Немного прокомментирую выполненное действие. Запись $II-2cdot I$ означает, что от элементов второй строки вычли соответствующие элементы первой строки, предварительно умноженные на два.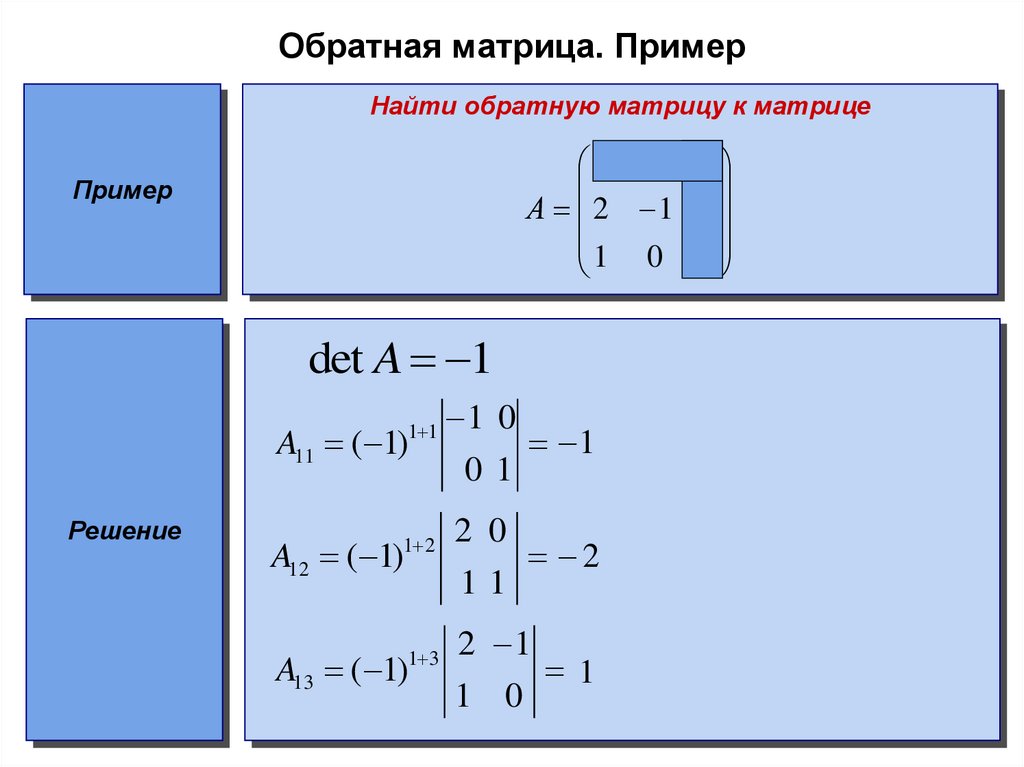
Для нахождения обратной матрицы в этом примере будем использовать те же операции, что применяются при решении систем линейных уравнений методом Гаусса. Подробные пояснения даны в , здесь же ограничимся краткими комментариями. Запишем расширенную матрицу: $left(begin{array} {cccc|cccc} -5 & 4 & 1 & 0 & 1 & 0 & 0 & 0 \
2 & 3 & -2 & 1 &0 &1&0 &0 \
0 & 7 & -4 & -3 &0 & 0 & 1 & 0\
1 & 4 & 0 & 6 &0 &0 & 0 & 1 end{array} right)$. Поменяем местами первую и четвёртую строки данной матрицы: $left(begin{array} {cccc|cccc}
1 & 4 & 0 & 6 &0 &0 & 0 & 1 \
2 & 3 & -2 & 1 &0 &1&0 &0 \
0 & 7 & -4 & -3 &0 & 0 & 1 & 0\
-5 & 4 & 1 & 0 & 1 & 0 & 0 & 0 end{array} right)$.
Для нахождения обратной матрицы применим операции, характерные методу Гаусса-Жордана. Отличие от метода Гаусса, рассмотренного в предыдущих примерах и , состоит в том, что решение осуществляется в один этап. Напомню, что метод Гаусса делится на 2 этапа: прямой ход («делаем» нули под главной диагональю матрицы до черты) и обратный ход (обнуляем элементы над главной диагональю матрицы до черты). Для вычисления обратной матрицы методом Гаусса-Жордана двух стадий решения не потребуется. Для начала составим расширенную матрицу: $(A|E)$:
$$
(A|E)=left(begin{array} {ccc|ccc} 2 & 3 & 4 & 1 & 0 & 0\ 7 & 1 & 9 & 0 & 1 & 0\ -4 & 5 & -2 &0 & 0 & 1 end{array} right)
$$
Первый шаг
Обнулим все элементы первого столбца кроме одного. В первом столбце все элементы отличны от нуля, посему можем выбрать любой элемент.
Выбранный элемент $(-4)$ находится в третьей строке, посему именно третью строку мы используем для обнуления выделенных элементов первого столбца:
Сделаем так, чтобы первый элемент третьей строки стал равен единице. Для этого разделим элементы третьей строки расширенной матрицы на $(-4)$:
Теперь приступим к обнулению соответствующих элементов первого столбца:
В дальнейших шагах использовать третью строку уже будет нельзя, ибо мы её уже применили на первом шаге.
Второй шаг
Выберем некий не равный нулю элемент второго столбца и обнулим все остальные элементы второго столбца. Мы можем выбрать любой из двух элементов: $frac{11}{2}$ или $frac{39}{4}$. Элемент $left(-frac{5}{4} right)$ выбрать нельзя, ибо он расположен в третьей строке, которую мы использовали на предыдущем шаге. Выберем элемент $frac{11}{2}$, который находится в первой строке. Сделаем так, чтобы вместо $frac{11}{2}$ в первой строке стала единица:
Теперь обнулим соответствующие элементы второго столбца:
В дальнейших рассуждениях первую строку использовать нельзя.
Третий шаг
Нужно обнулить все элементы третьего столбца кроме одного. Нам надо выбрать некий отличный от нуля элемент третьего столбца. Однако мы не можем взять $frac{6}{11}$ или $frac{13}{11}$, ибо эти элементы расположены в первой и третьей строках, которые мы использовали ранее. Выбор невелик: остаётся лишь элемент $frac{2}{11}$, который находится во второй строке. Разделим все элементы второй строки на $frac{2}{11}$:
Теперь обнулим соответствующие элементы третьего столбца:
Преобразования по методу Гаусса-Жордана закончены. Осталось лишь сделать так, чтобы матрица до черты стала единичной. Для этого придется менять порядок строк. Для начала поменяем местами первую и третью строки:
$$
left(begin{array} {ccc|ccc}
1 & 0 & 0 & 47/4 & -13/2 & -23/4 \
0 & 0 & 1 & -39/4 & 11/2 & 19/4 \
0 & 1 & 0 & 11/2 & -3 & -5/2 end{array} right)
$$
Теперь поменяем местами вторую и третью строки:
$$
left(begin{array} {ccc|ccc}
1 & 0 & 0 & 47/4 & -13/2 & -23/4 \
0 & 1 & 0 & 11/2 & -3 & -5/2 \
0 & 0 & 1 & -39/4 & 11/2 & 19/4 end{array} right)
$$
Итак, $A^{-1}=left(begin{array} {ccc}
47/4 & -13/2 & -23/4 \
11/2 & -3 & -5/2 \
-39/4 & 11/2 & 19/4 end{array} right)$.
Помогите решить / разобраться (Ф)
Сообщения без ответов | Активные темы | Избранное
| misha.physics |
СТО. Преобразование тензора электромагнитного поля. 16.10.2017, 23:19 |
|
17/03/17 |
Здравствуйте. Рассмотрим две СО: и . движеться относительно вдоль оси . Нужно записать етот тензор в системе . Первая матрица преобразовывает ковариантный индекс, значит ета матрица преобразовывает и базис, и у меня получается, что ета матрица преобразовывет компоненты 4-вектора от нового базиса к старому. Значит ета матрица обратная матрице . Теперь считаю верхний индекс строчкой, нижний — столбцом, разписываю какой-то елемент . Но ничего не изменяется. =. Но это как-бы понятно, так как у нас в формуле (1) две взаимно обратные матрицы. Но где все таки ошибка? В связи с этим, у меня вопросы: |
| Metford |
Re: СТО. Преобразование тензора электромагнитного поля. 16.10.2017, 23:43 |
|
06/04/13 |
misha. Но это как-бы понятно, так как у нас в формуле (1) две взаимно обратные матрицы. У них индексы не свёрнуты, так что ничего это не значит. Так Вы сейчас запретите преобразование любого тензора смешанного типа второй валентности. misha.physics в сообщении #1256227 писал(а): Можно ли имея дело с любым тензором валентности два (с компонентами или или ) считать его представленным матрицей и договориться какой индекс означает строку, а какой столбец? Можно. misha.physics в сообщении #1256227 писал(а): Как все-таки получить правильные формулы, типа и т.д.? Либо так, как Вы делали, либо как показано у Ландау во втором томе. Кстати, а у напряжённости электрического поля действительно есть множитель со скоростью света? Upd. Так. Вроде бы всё нормально получается. |
| misha.physics |
Re: СТО. Преобразование тензора электромагнитного поля. 17.10.2017, 00:08 |
|
17/03/17 |
Metford , спасибо за ваше внимание. Думаю, ето из-за системы единиц СИ появляется скорость света. Так как в ней напряженность ел. поля и индукция магн. поля имеют разные размерности. |
| Metford |
Re: СТО. Преобразование тензора электромагнитного поля. 17.10.2017, 00:12 |
|
06/04/13 |
misha. Думаю, ето из-за системы единиц СИ появляется скорость света. Вы в СИ считаете… (Сходил за валидолом, принял, слегка полегчало…) misha.physics в сообщении #1256247 писал(а): Просто меня удивило когда я считал, например E_{y’}E_y$. Ну, для -компонент так и будет. А с другими — пересчитайте. По идее должно получиться. Я не предлагаю выписывать сюда формулы: громоздко будет. |
| misha.physics |
Re: СТО. Преобразование тензора электромагнитного поля. 17.10.2017, 00:45 |
|
17/03/17 |
Да дело в том, что я этот тензор не сам выписал, а взял уже готовый 🙂 Просто решил проверить выкладки, которые были опущены. Завтра пересчитаю. Главное чтобы матрицы, которые я выписал были правильные. компоненты были равны, но вот другие меня смутили. |
misha. physics physics |
Re: СТО. Преобразование тензора электромагнитного поля. 17.10.2017, 15:06 |
|
17/03/17 |
Прошу прощения, все получилось. |
| maximav |
Re: СТО. 17.10.2017, 15:09 |
|
19/03/15 |
misha.physics в сообщении #1256227 писал(а): Хочу понять, почему у меня не получается осуществить преобразования Лоренца для тензора электромагнитного поля Тут все просто. Вы сначала договоритесь с самим собой, как вы превращаете вашу формулу (1) в форму матриц. То есть правило организации всех индексных значков там в ту табличку, которая вам нравится и вы хотите смотреть на нее, называя матрицой. Сделали это, причем и для и для . |
| EUgeneUS |
Re: СТО. 17.10.2017, 15:11 |
|
11/12/16 |
Metford ((Сходил за валидолом, принял, слегка полегчало…)) Валидол — плацебо, мятные конфетки. |
| Metford |
Re: СТО. 17.10.2017, 15:31 |
|
06/04/13 |
misha.physics в сообщении #1256346 писал(а): Вот такие иногда у меня бывают казусы. Со всеми случается. Главное, что всё получилось. Кстати, любопытства ради могли бы попробовать ещё упражнение похитрее. Мне в своё время очень помогло понять одну вещь важную. Таким манером можно вывести преобразование полей в общем случае, когда оси обеих систем расположены произвольным образом по отношению друг к другу. EUgeneUS (Оффтоп) Во-первых, для СИ и так сойдёт, а во-вторых, я принимаю подобные рекомендации исключительно от людей, отягощённых медицинским образованием. |
| EUgeneUS |
Re: СТО. Преобразование тензора электромагнитного поля. 17.10.2017, 15:37 |
|
11/12/16 |
Metford (мнение человека с медицинским образованием) Про валидол в самом начале раздела |
| Metford |
Re: СТО. 17.10.2017, 16:01 |
|
06/04/13 |
EUgeneUS (Оффтоп) Да мало ли кто что в интернете пишет. Тем более местами в таком игривом тоне. Предлагаю оффтоп закончить. В конце концов, какая разница, чем я себя травлю, особенно применительно к преобразованию тензора поля. |
misha. physics physics |
Re: СТО. Преобразование тензора электромагнитного поля. 17.10.2017, 20:40 |
|
17/03/17 |
maximav , спасибо, вы отлично прояснили мне етот момент (нюанс). Я уже тоже начал догадываться, что можно установить свое правило для представления тензоров, но ето правило должно быть применительно для всех тензоров. Но о линейности и т.д. я как-то не думал. Metford, если я правильно понял, то вы имеете ввиду написать прямую и обратную матрицы преобразований Лоренца для произвольной ориентации осей двух систем отсчета движущихся друг онтосительно друга. |
| Metford |
Re: СТО. Преобразование тензора электромагнитного поля. 17.10.2017, 20:44 |
|
06/04/13 |
Да, Вы верно поняли. |
Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию
| Страница 1 из 1 | [ Сообщений: 13 ] |
Модераторы: Eule_A, Pphantom, photon, Aer, whiterussian, Jnrty, profrotter, Парджеттер, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Разъёмы и пакеты.

1. Разъёмы и пакеты
1.1. Матрица преобразования
В общем случае, матрица преобразования координат задаётся в виде
произведения нескольких сомножителей:
I’=…·M3·M2·M1·I.
Например, можно заказать преобразование фазных величин в
симметричные составляющие по формуле (1.1), заменив на 3,
как это чаще делают в России. Это можно сделать, домножив матрицу
преобразования (1.1) на скаляр(ную матрицу) . Обе матрицы
имеются в файле, поставляемом вместе с программой МАСКАРАД, так что нужно будет
лишь указать на необходимость эти матрицы перемножить.
Для описания матриц преобразования координат и их сомножителей
отводится отдельный текстовый файл.
Достаточно часто приходится иметь дело не только с прямым, но и с
обратным преобразованием, например, не только с переходом от фазных координат к
симметричным составляющим, но и обратно. При этом в тестовый файл можно было бы
поместить две взаимно обратные матрицы.
программе предусмотрена возможность вычисления матрицы обратного преобразования
по матрице прямого преобразования. Нужно лишь указать, какая из матриц будет
фактически использоваться (возможно использование и обеих). Если матрица
прямого преобразования прямоугольна, под матрицей обратного преобразования
понимается псевдообратная по отношению к ней (см. (1.6) – (1.8)).
Следует иметь в виду, что при выполнении заказа на расчет мощностей
в фазах полюсов программе нужны их напряжения. Для их вычисления используется
матрица обратного преобразования. (Её использование не нарушает суммарной
мощности фаз любого полюса, что же касается полюсных фаз, то корректность
расчета их мощностей при использовании прямоугольных матриц может оценить
только пользователь – эту задачу нельзя решить формальными методами математики,
требуется анализ содержательной стороны.)
Таблица 4.1
Матрица преобразования
36 Имя имя преобразования (любой
текст)
3 Обрат «—>» –
признак генерации только прямого преобразования;
«<—» –
признак генерации только обратного преобразования;
«<->» –
признак генерации и прямого, и обратного преобразований
3 КолМат количество перемножаемых матриц
преобразования
3 (Адрес) адрес матрицы-сомножителя или
преобразования-сомножителя
1 (ТипАдр) способ задания сомножителя:
«#» – ссылкой на ранее описанное преобразование или
обратное ему;
не «#» – адресом описания матрицы
Номер обратного преобразования задается путем прибавления к номеру
прямого – числа 500.
1.2. Сомножитель матрицы преобразования
Матрицу-сомножитель не обязательно описывать как матрицу общего
вида, перечисляя все её элементы в виде комплексных чисел. Для вещественной
матрицы можно мнимых частей не указывать, не отводя под них места. Если матрица
скалярна (k·1), то ее можно задать одним числом k. И, наконец, предусмотрен еще один тип: упакованная матрица
инциденций. Остановимся на нем чуть подробнее.
Этот тип удобно использовать для описания схем соединения. Он-то,
собственно, и соответствует разъёму в общепринятом смысле этого слова. Так,
например, если мы хотим, соединить фазы 1 и 2 3-фазного полюса и подключить их
затем к 2-фазному узлу, как показано на рисунке, то закон преобразования токов
должен быть таким:
(1.1)
Матрица, описывающая схему соединения, состоящая из единиц и нулей,
называется матрицей инциденций. Для нее можно указать лишь расположение единиц,
которых бывает обычно немного, а не перечислять, чему равен каждый ее элемент:
для каждой единицы следует указать номер строки и столбца, где она расположена.
Такой способ описания схем соединения более нагляден.
Таблица 4.2
Первая запись пакета с описанием матрицы-сомножителя
3 Тип тип матрицы:
» :» –
комплексная матрица общего вида,
» .» –
вещественная матрица общего вида,
» 1″ –
упакованная матрица инциденций,
» k» –
комплексный скаляр
3 Ш ширина
поля, отводимого под одно число
3 Строк число строк (выводов со стороны
узла)
3 Столб число
столбцов (выводов со стороны П,Н)
Таблица 4.3
Записи, начиная со 2-й, для пакета с описанием сомножителя в
виде упакованной матрицы инциденций
Ш (i номер строки, где стоит
очередная единица
Ш j) номер
столбца, где она стоит
Каждая новая индексная пара располагается вслед за предыдущей (на
той же строке, если там, конечно, еще есть место).
нужно. Признаком конца списка служит нулевой номер строки. Об этом следует помнить
особенно в том случае, когда собственно список закончился в последней позиции
строки: нужно добавить ещё одну пустую строку.
Таблица 4.4
Записи, начиная со 2-й,для пакета с описанием
матрицы-сомножителя других типов
Ш*? (MATR) очередной элемент очередной
строки
(?=2 для комплексных элементов, ?=1 для вещественных)
Матрицы вводятся построчно: каждая строка – с новой записи.
Для преобразования (1.1)
пакет с описанием первого и единственного сомножителя матрицы преобразования
мог бы выглядеть, например, в одном из двух приведенных ниже вариантов:
123456789012 123456789012
1 2 2
3 . 2 2 2
1 1 1 2 2
3 1 1 0
0 0 1
1.3. Пакет разъёмов
Каждый полюс МП подключается к узлу через свой разъём.
разъёмов МП описывается в отдельном текстовом файле. Маска – это тоже
разъём.
Таблица 4.5
Пакет разъёмов
3 >> «>> » –
признак начала пакета
3 (Разъём) номер
разъёма для очередного полюса
1 ; «;» –
признак конца пакета
Номер разъёма – это адрес описывающей его матрицы
преобразования.
Что такое взаимно обратные числа?
Определение взаимно обратных чисел
С предыдущих уроков математики мы знаем: если прибавить или вычесть из числа нуль — оно не изменится. Точно также, если умножить или разделить число на единицу.
Ноль — нейтральный элемент для сложения и вычитания. При этом числа, которые в сумме дают ноль, называют противоположными.
- Например: 2 + (-2) = 0.
Единица — нейтральный элемент для умножения и деления. Поэтому симметричными называют числа, чье произведение дает единицу.
- Например: 3/5 * 5/3 = 1.
Два числа называют взаимно обратными, если их произведение равно 1.
Обратное число к данному числу — это такое число, которое мы умножаем на данное число и получаем единицу.
Если числа a и b взаимно обратные, то можно сказать, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Также можно говорить, что числу a обратно число b, а числу b обратно число a.
Приведем примеры взаимно обратных чисел. Так как произведение двух единиц равно 1, то по определению числа 1 и 1 — взаимно обратные.
Определение взаимно обратных чисел относится к любым числам — натуральным, целым, действительным, комплексным.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой.
Как найти число, обратное данному числу
На математике в 6 классе часто встречаются задания по нахождению числа, обратного данному. В общем случае число, обратное отличному от нуля числу a, записывается в виде дробного выражения 1/a или как a -1, так как и a * a-1 = 1. Но бывают случаи, когда 1/a можно сократить.
Иногда число, обратное данному числу, очевидно. Так бывает с натуральными числами и обыкновенными дробями. В других случаях приходится проводить вычисления. Например, с иррациональными и комплексными числами.
Рассмотрим каждый отдельный случай нахождения числа, обратного данному числу.
Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Число, обратное обыкновенной дроби
Числом, обратным обыкновенной дроби a/b, является дробь b/a.
Чтобы это проверить, выполним умножение обыкновенных дробей a/b и b/a — получим 1.
Если числитель и знаменатель дроби a/b поменять местами, то получится дробь b/a, обратная дроби a/b.
Это правило значительно экономит время. Можно сразу записать число, обратное данной обыкновенной дроби без каких-либо вычислений.
- Например, обратным числом дроби 7/9 является дробь 9/7, а число, обратное обыкновенной дроби 127/64, есть дробь 64/127.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Число, обратное натуральному числу
Нахождение числа, обратного данному натуральному числу, можно свести к нахождению числа, обратного дроби. Для этого нужно записать натуральное число как дробь со знаменателем 1.
Пусть нам дано натуральное число n, и нужно записать число, обратное числу n. Так как натуральное число n равно дроби n/1, то, поменяв местами числитель и знаменатель этой дроби, получим дробь 1/n, которая и является числом, обратным натуральному числу n.
Итак, натуральному числу n обратным числом является число 1/n, то есть, дробь с числителем 1 и знаменателем n. Значит n и 1/n — взаимно обратные числа.
- Например, узнаем, какое число взаимно обратное натуральному числу 20 — дробь 1/20, а число 1/6 — обратное натуральному числу 6.
Отдельно отметим число, обратное натуральному числу 1. Число, обратное единице, это единица. Пара взаимно обратных чисел 1 и 1 уникальна тем, что составляющие ее числа равны, других таких пар взаимно обратных чисел не существует.
Найти число, обратное смешанному числу
Напомним, что смешанное число выглядит так: A b/c. Чтобы найти число, обратное смешанному числу, нужно представить данное смешанное число в виде неправильной дроби, а уже после найти число, обратное этой дроби. Как это работает рассмотрим на примере.
Пример
Найти число, обратное смешанному числу
Как рассуждаем:
Сначала выполним перевод смешанного числа в неправильную дробь:
Число, обратное дроби 65/9, есть дробь 9/65.
Ответ: и 9/65 взаимно обратные числа.
Найти число, обратное десятичной дроби
Конечную десятичную дробь или периодическую десятичную дробь можно заменить обыкновенной дробью. Поэтому найти число, обратное конечной или периодической десятичной дроби, можно через поиск числа, которое обратно обыкновенной дроби. Разберемся на примерах.
Пример 1
Найти число, которое обратно десятичной дроби 5,128.
Как рассуждаем:
Переведем конечную десятичную дробь в обыкновенную:
Числом, обратным полученной дроби, является обыкновенная дробь 125/641. Это и есть решение задачи.
Ответ: 125/641.
Пример 2
Какое число является обратным для периодической десятичной дроби 2,(18)?
Как решаем:
Переведем периодическую десятичную дробь в обыкновенную:
Обратная дробь для 24/11 — 11/24. Значит, числом, обратным исходной десятичной дроби 2,(18), является дробь 11/24.
Ответ: 11/24.
Число, которое обратно бесконечной непериодической десятичной дроби принято записывать в виде дробного выражения с числителем 1 и знаменателем, равным заданной десятичной дроби. Например, бесконечной десятичной дроби 1,5639056242… обратно число 1/1,5639056242… .
Так как бесконечным непериодическим десятичным дробям отвечают иррациональные числа, то числа, которые обратны им, также записывают в виде дробных выражений.
Например, иррациональному числу обратно число , а иррациональному числу обратно число
Взаимно обратные числа с корнями
Важно запомнить, что вид взаимно обратных чисел может отличаться от a и 1/a. Поэтому нужно быть внимательным. Особенно это касается чисел, записи которых содержат знак корня. Рассмотрим на примере, как это бывает.
Пример
Проверить, можно ли назвать числа 4 — 2√3 и взаимно обратными.
Как решаем:
Вычислим произведение этих чисел:
Так как в ответе мы получили единицу и мы знаем, что произведение взаимно обратных чисел равно 1, значит эти числа можно назвать взаимно обратными.
Ответ: да, число взаимно обратны.
Взаимно обратные числа со степенями
Допустим, есть число, которое равно какой-то степени числа a. То есть, число a возведено в степень b. Обратным числу ab будет число a-b. Проверим.
И правда:
Пример
Написать число, обратное степени 6 -√7 + 2
Как рассуждаем:
Согласно предыдущему правилу, искомое число — 6 -(-√7 + 2) = 6 √7 — 2.
Ответ: 6 √7 — 2.
Взаимно обратные числа с логарифмами
У логарифма числа a по основанию b обратное число равно логарифму числа b по основанию a. То есть log b a и log a b — взаимно обратные числа.
Действительно, из свойств логарифма следует, что
, откуда log b a * log a b = 1.
Пример
Записать число, которое обратно логарифму числа 3 по основанию
Как решаем:
Число, обратное числу , выглядит так:
Ответ:
Найти число, обратное комплексному числу
Сейчас узнаем, как находить число, обратное комплексному числу z.
Если комплексное число задано в алгебраической форме, то есть, в виде z = x + i * y, то обратное ему число есть . Последнее выражение можно упростить, если умножить числитель и знаменатель на число x — i * y.
Пример 1
Найти число, обратное комплексному числу 4 + i.
Как решаем:
4 + i =
Умножим числитель и знаменатель полученного дробного выражения на число
4 + i.
Получим:
Ответ:
Когда комплексное число задано в тригонометрической форме как z = r * (cosφ + i * sinφ) или в показательной форме как z = r * e i*φ , то обратное ему число выглядит так
или
Действительно, и
Пример 2
Определить число, обратное комплексному числу
Как решаем:
В этом примере r = 2 и , откуда 1/r = 1/2 и
Следовательно, нужное нам обратное число равно
Являются ли числа взаимно обратными? Да, мы только что это доказали.
Ответ:
Неравенство с суммой взаимно обратных чисел
В математике есть специальная теорема о сумме взаимно обратных чисел — давайте ее сформулируем и узнаем ключевое свойство.
Теорема
Сумма двух положительных взаимно обратных чисел больше или равна 2.
Доказательство теоремы:
Нам известно, что среднее арифметическое положительных чисел a и b всегда больше или равно среднему геометрическому этих чисел, то есть,
Если в качестве b мы возьмем число, обратное a, то полученное неравенство будет выглядеть так: откуда и , что и требовалось доказать.
Пример
Вычислить сумму взаимно обратных чисел 2/3 и 3/2,
Как решаем:
Получили число больше 2.
Побочная диагональ главная диагональ — Студопедия
Поделись
Санкт-Петербург
Часть IV
ОПОРНЫЕ ЛЕКЦИИ ПО МАТЕМАТИКЕ
Э. Н. ОСИПОВА
КАФЕДРА МАТЕМАТИКИ
ТЕХНОЛОГИИ И ДИЗАЙНА
УНИВЕРСИТЕТ
ГОСУДАРСТВЕННЫЙ
САНКТ-ПЕТЕРБУРГСКИЙ
Российской Федерации
(МЕТОДИЧЕСКОЕ ПОСОБИЕ)
1 . МАТРИЦЫ
1.1. Основные понятия
Матрицей будем называть прямоугольную таблицу чисел, расположенных строками и столбцами; сами числа будем называть элементами матрицы , а число строк и число столбцов образуют размерность матрицы.
Приняты следующие обозначения.
— матрица размерностисодержит 2строки и 3столбца.
— матрица-строка (строка), содержит 1 строку.
— матрица-столбец (столбец), содержит 1столбец.
— матрица содержит mстрок и nстолбцов.
— означает, что i принимает все натуральные значения от 1 до n.
— элемент матрицы , расположенный на пересечении ее i -ой строки и j-го столбца; iи j называют индексами.
— нулевая матрица размерности .
Квадратной матрицей n -го порядка будем называть матрицу, содержащую
n строк и n столбцов.
Элементы , у которых образуют ее главную диагональ,
а если , то они образуют побочную диагональ.
— квадратная матрица 4-го порядка.
.
Квадратную матрицу будем называть треугольной, если все элементы, расположенные выше (либо ниже) главной диагонали равны нулю.
.
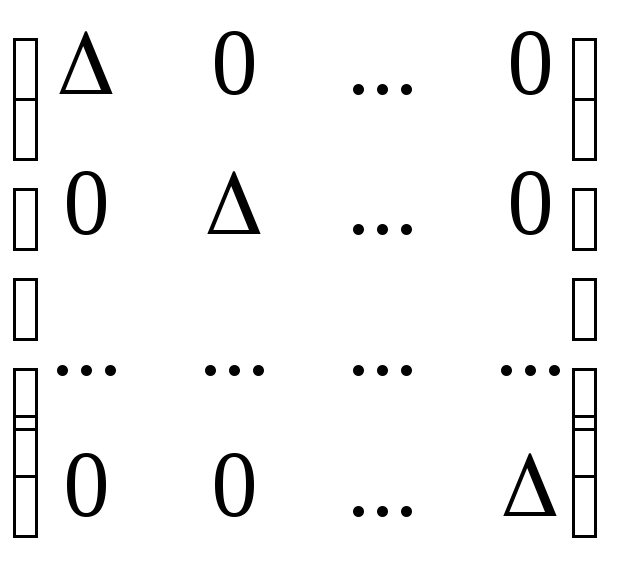
Квадратную матрицу будем называть диагональной, если все ее элементы, нерасположенные на главной диагонали равны нулю.
— диагональная матрица четвертого порядка.
Диагональную матрицу будем называть единичной, если все элементы главнойдиагонали равны 1.
— единичная матрица пятого порядка.
Элементы двух матриц будем называть соответствующими, если они имеют одинаковые индексы. Строки (столбцы) будем называть соответствующими, если они имеют одинаковый номер.
Транспонированием матрицы будем называть операцию замены всех столбцовсоответствующими строками
(всех строк соответствующими столбцами).
второй столбец
первый столбец
Матрицу будем называть симметрической (симметричной), если при транспонировании она не изменяется.
Из определения следует:
— симметрическая матрица может быть только квадратной;
— ее элементы расположены симметрично относительно главной диагонали.
.
Две матрицы одинаковой размерности будем называть равными , если все их соответствующие элементы равны.
1.2. Действия с матрицами
Суммой двух матриц одинаковой размерности(А + В) будем называтьновую матрицу ( Х )той же размерности , каждый элемент которой равен сумме соответствующих элементов матриц-слагаемых.
Произведением матрицы А на скаляр l ( l× А )будем называтьновую матрицу ( Х )той же размерности, каждый элемент которой равен произведению соответствующего элемента данной матрицы на данный скаляр.
Из последних двух определений следует что разность двух матриц может быть найдена следующим образом:
Скалярным произведением двух строк (или двух столбцов, или строки и столбца), имеющих одинаковое количество элементов, будем называть число, равное сумме произведений всех соответствующих элементов.
Линейной комбинацией строк (столбцов) будем называть сумму произведений этих строк (столбцов) на вещественные числа (скаляры).
Сами числа при этом называют коэффициентами этой линейной комбинации.
Произведением двух матриц будем называть новую матрицу , у которой каждый элемент хijравен скалярному произведению i — ойстроки первого сомножителя на j -й столбец второго сомножителя.
Из определения следуют свойства:
1.2.1. Количество столбцов матрицы-множимого должно быть равно количеству строк матрицы-множителя;
1.2.2. Матрица-произведение имеет столько строк, сколько их у матрицы-множимого и столько столбцов, сколько их у матрицы-множителя.
1.2.3. Умножение матриц не подчиняется переместительному закону.
1.2.4. Квадратные матрицы можно умножать только, если они имеют одинаковый порядок.
1.2.5. Умножение квадратной матрицы на единичную матрицу и слева и справа не изменяет данную матрицу.
;
Две квадратные матрицы будем называть взаимно обратными, если их произведение равно единичной матрице.
Взаимно обратные матрицы обычно обозначают так: АиА-1.
Произведение главной диагонали матрицы
Содержание
- 1 Матрица строка
- 2 Матрица столбец
- 3 Нулевая матрица
- 4 Квадратная матрица
- 5 Главная диагональ матрицы
- 6 Побочная диагональ матрицы
- 7 Диагональная матрица
- 8 Единичная матрица
- 9 След матрицы
- 10 Верхняя треугольная матрица
- 11 Нижняя треугольная матрица
- 12 Ядро или нуль пространство матрицы
- 13 Противоположная матрица
- 14 Кососимметричная (Кососимметрическая) матрица
- 15 Разность матриц
- 16 Степень матрицы
- 17 Симметричная (Симметрическая) матрица
- 18 Обозначение
- 19 Элементы матрицы
- 20 Диагонали
Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.
Матрица порядка m × n записывается в форме:
или (i=1,2. m; j=1,2. n).
Числа aij входящие в состав данной матрицы называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j— номер столбца.
Матрица строка
Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:
Матрица столбец
Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например
Нулевая матрица
Если все элементы матрицы равны нулю,то матрица называется нулевой матрицей . Например
Квадратная матрица
Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:
Главная диагональ матрицы
Элементы расположенные на местах a 11, a 22 . ann образуют главную диагональ матрицы. Например:
В случае m×n -матриц элементы aii ( i= 1,2. min(m,n)) также образуют главную диагональ. Например:
Элементы расположенные на главной диагонали называются главными диагональными элементами или просто диагональными элементами .
Побочная диагональ матрицы
Элементы расположенные на местах a 1n, a 2n-1 . a n1 образуют побочную диагональ матрицы. Например:
Диагональная матрица
Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:
Единичная матрица
Квадратную матрицу n-го порядка, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю, называется единичной матрицей и обозначается через E или E n , где n — порядок матрицы. Единичная матрица порядка 3 имеет следующий вид:
След матрицы
Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:
Верхняя треугольная матрица
Квадратная матрица порядка n×n называется верхней треугольной матрицей, если равны нулю все элементы матрицы, расположенные под главной диагональю, т.е. aij=0, при всех i>j . Например:
Нижняя треугольная матрица
Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. aij=0, при всех i T ).
Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).
Ядро или нуль пространство матрицы
Множесто всех решений уравнения Ax=0, где A- mxn-матрица, x— вектор длины n — образует нуль пространство или ядро матрицы A и обозначается через Ker(A) или N(A).
Противоположная матрица
Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.
Кососимметричная (Кососимметрическая) матрица
Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:
В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.
Пример кососимметрической матрицы:
Разность матриц
Разностью C двух матриц A и B одинакового размера определяется равенством
Для обозначения разности двух матриц используется запись:
Степень матрицы
Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:
где E-единичная матрица.
Из сочетательного свойства умножения следует:
где p,q— произвольные целые неотрицательные числа.
Симметричная (Симметрическая) матрица
Матрица, удовлетворяющая условию A=A T называется симметричной матрицей.
Для симметричных матриц имеет место равенство:
Матрицей размера $m imes n$ называется прямоугольная таблица, содержащая $m cdot n$ чисел, состоящая из $m$ строк и $n$ столбцов.
Обозначение
Таблица берется либо в круглые скобки, либо окружается двумя параллельными вертикальными прямыми.
Если матрица содержит $m$ строк и $n$ столбцов, то матрица называется матрицей размера $m imes n$ или $m imes n$-матрицей. Размер матрицы указывается справа внизу возле ее имени, либо таблицы с обозначением элементов.
Элементы матрицы
Элементы матрицы $A$ обозначаются $a_$, где $i$ — номер строки, в которой находится элемент, а $j$ — номер столбца.
Задание. Чему равен элемент $a_<23>$ матрицы $A=left( egin <1>& <4>& <0> <-1>& <3>& <7>end
ight)$ ?
Решение. Находим элемент, который стоит на пересечении второй строки и третьего столбца:
Таким образом, $a_ <23>= 7$.
Ответ. $a_ <23>= 7$
Строка матрицы называется нулевой, если все ее элементы равны нулю. Если хотя бы один из элементов строки не равен нулю, то строка называется ненулевой.
Замечание. Аналогичное определение и для нулевого и ненулевого столбцов матрицы.
Диагонали
Главной диагональю матрицы называется диагональ, проведённая из левого верхнего угла матрицы в правый нижний.
Побочной диагональю матрицы называется диагональ, проведённая из левого нижнего угла матрицы в правый верхний.
: 1 и 6 — элементы главной диагонали.
: 3 и 4 — элементы побочной диагонали.
Для матрицы элементы 1, 2, -1 образуют главную диагональ; а элементы 3, 2, 2 — побочную.
Санкт-Петербург
Часть IV
ОПОРНЫЕ ЛЕКЦИИ ПО МАТЕМАТИКЕ
Э. Н. ОСИПОВА
КАФЕДРА МАТЕМАТИКИ
ТЕХНОЛОГИИ И ДИЗАЙНА
УНИВЕРСИТЕТ
ГОСУДАРСТВЕННЫЙ
САНКТ-ПЕТЕРБУРГСКИЙ
Российской Федерации
(МЕТОДИЧЕСКОЕ ПОСОБИЕ)
1 . МАТРИЦЫ
1.1. Основные понятия
Матрицей будем называть прямоугольную таблицу чисел, расположенных строками и столбцами; сами числа будем называть элементами матрицы , а число строк и число столбцов образуют размерность матрицы.
Приняты следующие обозначения.
— матрица размерностисодержит 2строки и 3столбца.
— матрица-строка (строка), содержит 1 строку.
— матрица-столбец (столбец), содержит 1столбец.
— матрица содержит mстрок и nстолбцов.
— означает, что i принимает все натуральные значения от 1 до n.
— элемент матрицы , расположенный на пересечении ее i -ой строки и j-го столбца; iи j называют индексами.
— нулевая матрица размерности .
Квадратной матрицей n -го порядка будем называть матрицу, содержащую
n строк и n столбцов.
Элементы , у которых образуют ее главную диагональ,
а если , то они образуют побочную диагональ.
— квадратная матрица 4-го порядка.
.
Квадратную матрицу будем называть треугольной, если все элементы, расположенные выше (либо ниже) главной диагонали равны нулю.
.
Квадратную матрицу будем называть диагональной, если все ее элементы, нерасположенные на главной диагонали равны нулю.
— диагональная матрица четвертого порядка.
Диагональную матрицу будем называть единичной, если все элементы главнойдиагонали равны 1.
— единичная матрица пятого порядка.
Элементы двух матриц будем называть соответствующими, если они имеют одинаковые индексы. Строки (столбцы) будем называть соответствующими, если они имеют одинаковый номер.
Транспонированием матрицы будем называть операцию замены всех столбцовсоответствующими строками
(всех строк соответствующими столбцами).
Матрицу будем называть симметрической (симметричной), если при транспонировании она не изменяется.
Из определения следует:
— симметрическая матрица может быть только квадратной;
— ее элементы расположены симметрично относительно главной диагонали.
.
Две матрицы одинаковой размерности будем называть равными , если все их соответствующие элементы равны.
1.2. Действия с матрицами
Суммой двух матриц одинаковой размерности(А + В) будем называтьновую матрицу ( Х )той же размерности , каждый элемент которой равен сумме соответствующих элементов матриц-слагаемых.
Произведением матрицы А на скаляр l ( l× А )будем называтьновую матрицу ( Х )той же размерности, каждый элемент которой равен произведению соответствующего элемента данной матрицы на данный скаляр.
Из последних двух определений следует что разность двух матриц может быть найдена следующим образом:
Скалярным произведением двух строк (или двух столбцов, или строки и столбца), имеющих одинаковое количество элементов, будем называть число, равное сумме произведений всех соответствующих элементов.
Линейной комбинацией строк (столбцов) будем называть сумму произведений этих строк (столбцов) на вещественные числа (скаляры).
Сами числа при этом называют коэффициентами этой линейной комбинации.
Произведением двух матриц будем называть новую матрицу , у которой каждый элемент хijравен скалярному произведению i — ойстроки первого сомножителя на j -й столбец второго сомножителя.
Из определения следуют свойства:
1.2.1. Количество столбцов матрицы-множимого должно быть равно количеству строк матрицы-множителя;
1.2.2. Матрица-произведение имеет столько строк, сколько их у матрицы-множимого и столько столбцов, сколько их у матрицы-множителя.
1.2.3. Умножение матриц не подчиняется переместительному закону.
1.2.4. Квадратные матрицы можно умножать только, если они имеют одинаковый порядок.
1.2.5. Умножение квадратной матрицы на единичную матрицу и слева и справа не изменяет данную матрицу.
;
Две квадратные матрицы будем называть взаимно обратными, если их произведение равно единичной матрице.
Взаимно обратные матрицы обычно обозначают так: АиА -1 .
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась — это был конец пары: «Что-то тут концом пахнет». 8516 — | 8102 — или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
линейная алгебра — Нахождение обратной матрицы
Задавать вопрос
Спросил
8 лет, 10 месяцев назад
Изменено
8 лет, 10 месяцев назад
Просмотрено
1к раз
$begingroup$
Этот вопрос входит в мое задание. Нам не разрешено использовать какой-либо символ для представления каких-либо элементарных операций со строками и столбцами, используемых в решении. Мы должны решить ее шаг за шагом. Пожалуйста, помогите мне проверить мое решение слово за словом, включая мою орфографию и грамматику.
Вопрос:
Найдите обратное число
$$A=begin{pmatrix}2& 2& 3\ 2& 5& 3\ 1& 0& 8end{pmatrix}$$
, используя только элементарные операции со строками.
Решение:
Начнем с формирования матрицы $begin{pmatrix} A & | & I_3 end{pmatrix}=left(begin{array}{ccc|ccc}2 & 2 & 3 & 1 & 0 & 0\2 & 5 & 3 & 0 & 1 & 0\1 & 0 & 8 & 0 & 0 & 1end{массив}right)$. Поменяв местами первую и третью строки матрицы $begin{pmatrix} A & | & I_3 end{pmatrix}$ получаем матрицу $left(begin{array}{ccc|ccc}1 & 0 & 8 & 0 & 0 & 1\2 & 5 & 3 & 0 & 1 & 0\2 & 2 & 3 & 1 & 0 & 0end{массив}right)$. Сложение $(-2)$, умноженное на первую строку матрицы $left(begin{array}{ccc|ccc}1 & 0 & 8 & 0 & 0 & 1\2 & 5 & 3 & 0 & 1 & 0\2 & 2 & 3 & 1 & 0 & 0end{array}right)$ во вторую его строку, получаем матрицу $left(begin{array}{ccc|ccc}1 & 0 & 8 & 0 & 0 & 1\0 & 5 & -13 & 0 & 1 & -2\2 & 2 & 3 & 1 & 0 & 0end{массив}right)$. Умножение второй строки матрицы $left(begin{array}{ccc|ccc}1 & 0 & 8 & 0 & 0 & 1\0 & 5 & -13 & 0 & 1 & -2\2 & 2 & 3 & 1 & 0 & 0end{array}right)$ на $frac{1}{5}$ получаем матрицу $left(begin{array}{ccc|ccc}1 & 0 & 8 & 0 & 0 & 1\0 & 1 & -frac{13}{5} & 0 & frac{1}{5} & -frac{2}{5}\2 & 2 & 3 & 1 & 0 & 0end{массив}right)$. Сложение $(-2)$, умноженное на первую строку матрицы $left(begin{array}{ccc|ccc}1 & 0 & 8 & 0 & 0 & 1\0 & 1 & -frac{13 {5} & 0 & frac{1}{5} & -frac{2}{5}\2 & 2 & 3 & 1 & 0 & 0end{array}right)$ до третьего строки получаем матрицу $left(begin{array}{ccc|ccc}1 & 0 & 8 & 0 & 0 & 1\0 & 1 & -frac{13}{5} & 0 & frac{1}{5} & -frac{2}{5}\0 & 2 & -13 & 1 & 0 & -2end{массив}right)$. Сложение $(-2)$, умноженное на вторую строку матрицы $left(begin{array}{ccc|ccc}1 & 0 & 8 & 0 & 0 & 1\0 & 1 & -frac{13 {5} & 0 & frac{1}{5} & -frac{2}{5}\0 & 2 & -13 & 1 & 0 & -2end{array}right)$ до его третья строка, мы получаем матрицу $left(begin{array}{ccc|ccc}1 & 0 & 8 & 0 & 0 & 1\0 & 1 & -frac{13}{5} & 0 & frac{1}{5} & -frac{2}{5}\0 & 0 & -frac{39{5} & 1 & -frac{2}{5} & -frac{6}{5}end{массив}right)$.
Умножение третьей строки матрицы $left(begin{array}{ccc|ccc}1 & 0 & 8 & 0 & 0 & 1\0 & 1 & -frac{13}{5} & 0 & frac{1}{5} & -frac{2}{5}\0 & 0 & -frac{39}{5} & 1 & -frac{2}{5} & -frac{ 6}{5}end{array}right)$ на $(-frac{5}{39})$ получаем матрицу $left(begin{array}{ccc|ccc}1 & 0 & 8 & 0 & 0 & 1\0 & 1 & -frac{13}{5} & 0 & frac{1}{5} & -frac{2}{5}\0 & 0 & 1 & -фракция{5}{39} & frac{2}{39} & frac{2}{13}end{массив}right)$. Сложение $(frac{13}{5})$, умноженное на третью строку матрицы $left(begin{array}{ccc|ccc}1 & 0 & 8 & 0 & 0 & 1\0 & 1 & -frac{13}{5} & 0 & frac{1}{5} & -frac{2}{5}\0 & 0 & 1 & -frac{5}{39} & frac{2}{39} & frac{2}{13}end{array}right)$ во вторую его строку, получим матрицу $left(begin{array}{ccc|ccc}1 & 0 & 8 & 0 & 0 & 1\0 & 1 & 0 & -frac{1}{3} & frac{1}{3} & 0\0 & 0 & 1 & -frac{5 {39} & frac{2}{39} & frac{2}{13}end{массив}right)$. Добавление $(-8)$ к третьей строке матрицы $left(begin{array}{ccc|ccc}1 & 0 & 8 & 0 & 0 & 1\0 & 1 & 0 & -frac {1}{3} & frac{1}{3} & 0\0 & 0 & 1 & -frac{5}{39} & frac{2}{39} & frac{2}{ 13}end{array}right)$ на его первую строку, получаем матрицу $left(begin{array}{ccc|ccc}1 & 0 & 0 & frac{40}{39} & — frac{16}{39} & -frac{3}{13}\0 & 1 & 0 & -frac{1}{3} & frac{1}{3} & 0\0 & 0 & 1 & -frac{5}{39{-1}A$ и каждый раз получал $I_3$.
И это подтверждается и здесь.
Ваше решение правильное, очень хорошо написано, и за ним легко следовать (хотя есть за чем следить!).
$endgroup$
$begingroup$
Ваше решение верно.$ $
$endgroup$
$begingroup$
Мне кажется, все в порядке. Я не уверен, сколько еще вы ожидаете от ответа. В качестве совета: в конце вы можете на самом деле перемножить две матрицы, чтобы убедиться, что они взаимно обратны.
$endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Обратная функция – определение, расчет и график
Прежде всего мы должны определить обратные функции и объяснить их назначение. Вы должны знать, что только инъективных функций могут иметь свои обратные .
Инъективность функции
Мы говорим, что функция $f$ обладает свойством инъективности или что она является инъекционной, если верно следующее: (x_1) neq f(x_2) }$.
Это означает, что функция внедряется, если она сопоставляет разные номера своего домена с разными членами кодового домена. Это свойство эквивалентно следующему:
$ f(x_1)=f(x_2) Longrightarrow x_1=x_2$ .
Значение: функция является инъекционной, если из равенства значений функции следует равенство аргументов.
Существует очень простой способ узнать, является ли некоторая функция инъективной или нет. Мы будем использовать простой метод, называемый горизонтальное испытание .
Горизонтальный критерий инъективности
Функция $f $ является инъективной, если прямая, параллельная оси x, пересекает ее график не более чем в одной точке.
Мы покажем вам, как использовать горизонтальный тест для следующих функций:
$f(x)=|x|, b(x)=frac { 1 }{ x } $
Горизонтальный тест показывает, что если мы можем нарисовать любую горизонтальную линию и если эта линия пересекает график только в одной точке, функция будет инъекционной.
Теперь просто нарисуем несколько горизонтальных линий и посмотрим, что получится.
Можно заметить, что если мы возьмем функцию $f(x)= |x|$ и проведем через нее горизонтальные прямые, то эти прямые пересекают функцию в двух точках. Каждая линия, которую мы проводим на положительной части оси $y$, будет пересекать эту функцию в двух точках. Таким образом эта функция $f(x)=|x|$ не является инъекцией.
Таким же образом можно проверить функцию $b(x)=frac { 1 }{ x } $. Эта функция будет инъективной, потому что мы не можем провести горизонтальную линию, пересекающую эту функцию в двух точках.
Функция не может иметь обратную функцию, если она не является инъекцией. Таким образом, если функция является инъекцией, то для заданного $y$ из образа функции существует единственный $x$ из области определения функции такой, что и справедливо $f(x)=y$. Эта уникальность обеспечивается свойством инъективности, иначе существовали бы два числа $x_1$ и $x_2$, которые отображаются в одно и то же $y$, а это означает, что функция $f$ не может быть инъекцией.
Это означает, что мы можем найти отображение $g$, которое переводит $y$ в $x$, $g(y)=x$. Для этой пары отображений $f $ и $g$ верно, что: 9{-1}$.
Поэтому мы говорим, что функции $f$ и $g$ взаимно обратны .
Отношения:
$g(f(x))=x$, для каждого x∈$D_f$
$f(g(x))=x$, для каждого x ∈$D_g$
можно также записать как:
$y=f(x) leftrightarrow x=g(y)$, $forall xin D_f$, $forall xin D_g$
Если функция $f$ отображает элемент $x$ в элемент $y$, обратная функция отображает элемент $y$ в элемент $x$. 9{-1}(у)$ .
Из уравнения $y=f(x)$ мы должны вычислить значение переменной $x$ по отношению к переменной $y$. Если бы мы могли это сделать, мы могли бы получить уравнение обратной функции.
Пример 1 . Найдите обратную функцию функции $f(x)=5x+2$.
Сначала мы напишем это уравнение, как если бы $f(x)=y$.
$y=5x+2$
Теперь решим это уравнение с неизвестным $x$.
$x=frac{y-2}{5}$
9{2}+1=5 rightarrow $ эта функция не является инъекцией.
График обратной функции
Можем ли мы определить график обратной функции функции $f$, если мы знаем график функции $f$?
Начнем снова с основ: $ y=f(x) leftrightarrow x=g(y)$ мы можем прочитать следующее:
Точка $(x, y)$ лежит на графике функции f тогда и только тогда, когда точка $(y, x)$ лежит на графике функции $g$. 9{-1}(х)$.
Объяснение урока: обратная матрица 2 × 2
В этом объяснении мы узнаем, как проверить, имеет ли матрица 2 × 2 обратную, а затем найти ее обратную,
если возможно.
При работе с действительными системами счисления мы знаем, что умножение любого отличного от нуля числа на его обратное значение 1. 1 является особым
действительное число, потому что умножение любого числа на 1 не меняет числа. В этом смысле 1 называется мультипликативной идентичностью. Обратная величина ненулевого числа называется обратной мультипликативной.
Мы можем убедиться в полезности обратной мультипликативной функции, когда решим линейное уравнение, чтобы найти неизвестную константу. Например,
рассмотрим задачу нахождения значения 𝑥, удовлетворяющего уравнению
3𝑥=6.
Мы можем решить это уравнение, просто разделив обе части уравнения на 3. Деление на 3 равносильно умножению на
13, что является обратным числом 3. На самом деле здесь происходит то, что мы умножаем оба
стороны уравнения мультипликативным обратным 3, который является коэффициентом неизвестной константы 𝑥. Это ведет к
13×3×𝑥=13×6.
Умножение 3 на его обратное значение дает 1, что является мультипликативным тождеством. Итак, левая часть уравнения
становится 1×𝑥, что совпадает с 𝑥. Это приводит к 𝑥=2, что
дает значение неизвестной константы.
Теперь давайте подумаем о задаче аналогичного типа с использованием матричных операций. Скажем, что мы знаем две матрицы 𝐴
и 𝐵 и мы хотим найти неизвестную матрицу 𝑋, которая удовлетворяет матричному уравнению
𝐴𝑋=𝐵.
Вспоминая процесс решения в контексте операций с действительными числами, мы хотели бы «разделить» обе стороны
по 𝐴. Но мы не знаем понятия деления в матричных операциях. Вместо разделения мы можем думать о
умножение обеих частей уравнения на «обратное» 𝐴, только если такой объект, как
может быть определена обратная или мультипликативная обратная матрица.
Цель этого объяснения как раз и состоит в том, чтобы понять, когда можно найти мультипликативную обратную величину
Матрица 2 × 2 и узнать, как вычислить обратную, когда это возможно. Для обсуждения мультипликативного
обратной матрицы, нам нужно сначала понять мультипликативную идентичность.
Напомним, что единичная матрица, обозначаемая 𝐼 или 𝐼, представляет собой диагональную матрицу, диагональ которой
элементы равны 1. Мы знаем, что умножение любой матрицы на единичную матрицу совместимого порядка не меняет матрицу. Следовательно, единичная матрица является мультипликативной идентичностью для умножения матриц. Это означает, что мы можем определить (мультипликативное)
обратная матрица, так что умножение матрицы на ее обратную приводит к единичной матрице. В частности, нам понадобится
Единичная матрица 2 × 2 𝐼=1001 в
чтобы определить обратную матрицу 2 × 2.
Определение: обратная матрица
Пусть 𝐴 — матрица 2×2. Обратное к 𝐴, обозначаемое
𝐴 — матрица, удовлетворяющая
𝐴𝐴=𝐼,𝐴𝐴=𝐼.
Если такая матрица существует, то говорят, что матрица 𝐴 обратима.
Если такой матрицы не существует, говорят, что матрица 𝐴 необратима.
Напомним, что умножение матрицы 𝑚×𝑛 на матрицу 𝑛×𝑘 дает
в матрице 𝑚×𝑘. Поскольку и 𝐴, и 𝐼 равны 2×2
матриц, это означает, что обратная 𝐴, если она существует, также должна быть матрицей 2×2. Фактически, это определение обратной матрицы справедливо для больших матриц, если они квадратные, заменяя
2 на 𝑛 в заявлении. В этом объяснении мы сосредоточимся на случае 𝑛=2.
Мы можем видеть, что обратная или мультипликативная обратная матрица определяется таким образом, что умножение любой матрицы
по его обратным результатам в единичной матрице. Таким образом, обратная матрица аналогична обратной величине ненулевого
настоящий номер.
Мы знаем, что умножение матриц не является коммутативным, а это значит, что порядок умножения имеет значение. Таким образом, нам нужны оба
𝐴𝐴 и 𝐴𝐴 равны тождеству.
Это определение говорит нам, что обратной матрицей 2×2 является другая матрица 2×2, такая как
что умножение двух матриц в любом порядке приводит к единичной матрице 𝐼. Если такая матрица
𝐴 существует, сразу видно, что исходная матрица 𝐴 удовлетворяет определению
инверсия 𝐴. Это приводит к следующему свойству.
Свойство: обратная матрица, обратная
Пусть 𝐴 — обратимая матрица. Тогда 𝐴 обратимо и
𝐴=𝐴.
Прежде чем обсуждать, как найти обратную матрицу, нам нужно понять, когда матрица необратима. В контексте
операций с действительными числами, единственным необратимым действительным числом является 0. Аналогом действительного числа 0 является нулевая матрица, обозначаемая
𝑂, все элементы которой равны 0. Хотя нулевая матрица необратима, существуют и большие
семейства необратимых матриц.
Свойство: сингулярные матрицы
Квадратная матрица необратима тогда и только тогда, когда ее определитель равен нулю. Матрицы с этим свойством называются
сингулярные матрицы.
Чтобы понять это утверждение, напомним свойство определителей матрицы. Даны квадратные матрицы 𝐵
и 𝐶 того же порядка,
detdetdet(𝐵𝐶)=(𝐵)×(𝐶).
Мы можем использовать это свойство в первом уравнении в определении обратной матрицы: если 𝐴 является обратимым
матрица, у нас есть
𝐴𝐴=𝐼.
Взяв определитель обеих частей этого уравнения,
detdet𝐴𝐴=(𝐼).
Мы знаем, что определитель единичной матрицы равен 1. Используя свойство определителя, это уравнение может быть
написано как
detdet(𝐴)×𝐴=1.
Поскольку det(𝐴) является одним из множителей в левой части уравнения, это уравнение не может
удовлетворяться, если det(𝐴)=0. Другими словами, условие 𝐴𝐴=𝐼 не может
верно для любой матрицы 𝐴, если det(𝐴)=0. Это доказывает, что 𝐴
необратим, если det(𝐴)=0.
Этот аргумент только показывает, что матрица с нулевым определителем необратима. Мы не будем здесь доказывать обратное утверждение, т.
в котором говорится, что матрица с ненулевым определителем обратима. Вместо этого мы разработаем формулу для нахождения обратного
невырожденных матриц, что будет служить доказательством существования обратной.
Прежде чем углубиться в это обсуждение, давайте рассмотрим несколько примеров, где мы будем определять, является ли данная матрица
обратим.
Пример 1: Детерминанты и обратимость
Является ли матрица 31−31 обратимой?
Ответ
В этом примере нам нужно определить, является ли данная матрица обратимой. Напомним, что квадратная матрица обратима, если
и только если его определитель не равен нулю. Мы видим, что порядок данной матрицы 2×2,
что означает, что это квадратная матрица. Итак, нам нужно проверить его определитель, чтобы увидеть, равен ли он нулю.
Напомним, что определитель матрицы 2×2 определяется выражением
det𝑎𝑏𝑐𝑑=𝑎×𝑑−𝑏×𝑐.
Это приводит к
det31−31=3×1−1×(−3)=6.
Мы видим, что определитель данной квадратной матрицы отличен от нуля. Это говорит нам, что эта матрица обратима.
Следовательно, правильный ответ на вопрос в этом примере — да.
Рассмотрим еще один пример, в котором мы определяем, является ли данная матрица обратимой.
Пример 2: Детерминанты и обратимость
Является ли матрица 31−3−1 обратимой?
Ответ
В этом примере нам нужно определить, является ли данная матрица обратимой. Напомним, что квадратная матрица обратима, если
и только если его определитель не равен нулю. Мы видим, что порядок данной матрицы 2×2,
что означает, что это квадратная матрица. Итак, нам нужно проверить его определитель, чтобы увидеть, равен ли он нулю.
Напомним, что определитель матрицы 2×2 задается выражением
det𝑎𝑏𝑐𝑑=𝑎×𝑑−𝑏×𝑐.
Это приводит к
det31−3−1=3×(−1)−1×(−3)=0.
Мы видим, что определитель данной квадратной матрицы равен нулю. Это говорит нам о том, что данная матрица необратима.
Следовательно, правильный ответ на вопрос в этом примере — нет.
В следующем примере мы найдем условие для неизвестной константы в матрице при условии, что матрица обратима.
Пример 3: Детерминанты и обратимость
Учитывая, что матрица 71−7𝑎
обратимо, что должно быть верно для 𝑎.
Ответ
В этом примере нам дано, что матрица обратима. Напомним, что квадратная матрица обратима тогда и только тогда, когда ее
определитель не равен нулю. Мы видим, что порядок данной матрицы равен 2×2, что означает, что
это квадратная матрица. Итак, нам нужно убедиться, что его определитель не равен нулю, чтобы гарантировать, что он обратим.
Напомним, что определитель матрицы 2×2 задается выражением
det𝑎𝑏𝑐𝑑=𝑎×𝑑−𝑏×𝑐.
Это приводит к
det71−7𝑎=7×𝑎−1×(−7)=7𝑎+7.
Следовательно, определитель данной матрицы равен 7𝑎+7. Поскольку матрица обратима, это значение не должно равняться
нуль. Это ведет к
7𝑎+7≠07𝑎≠−7𝑎≠−1.
Следовательно, должно быть верно, что
𝑎≠−1.
В следующем примере мы найдем все возможные значения неизвестного в матрице, если известно, что матрица вырожденная.
Пример 4. Нахождение неизвестных элементов сингулярной матрицы
Найдите множество действительных значений (𝑥), составляющих матрицу
𝑥−382𝑥+3
единственное число.
Ответ
В этом примере нам дано, что матрица вырожденная. Напомним, что сингулярная матрица — это квадратная матрица с нулем
определитель. Мы видим, что порядок данной матрицы 2×2, что означает, что это квадрат
матрица. Итак, нам нужно убедиться, что его определитель равен нулю.
Напомним, что определитель матрицы 2×2 задается выражением
det𝑎𝑏𝑐𝑑=𝑎×𝑑−𝑏×𝑐.
Это приводит к
det𝑥−382𝑥+3=(𝑥−3)×(𝑥+3)−8×2.
Мы можем раскрыть это выражение через круглые скобки, используя формулу разности квадратов,
(𝑎+𝑏)(𝑎−𝑏)=𝑎−𝑏. Используя эту формулу, мы можем записать определитель как
𝑥−3−16=𝑥−25.
Следовательно, определитель данной матрицы равен 𝑥−25. Поскольку это сингулярная матрица, ее определитель должен
равен нулю. Это ведет к
𝑥−25=0𝑥=25𝑥=±5.
Следовательно, мы должны иметь либо 𝑥=5, либо 𝑥=−5. Множество реальных значений
(𝑥), для которых данная матрица вырождена, есть
{−5,5}.
До сих пор мы рассмотрели несколько примеров, касающихся существования обратной матрицы. Обратим внимание на поиск
обратная матрица 2 × 2.
В следующем примере мы определим, являются ли две заданные матрицы обратными друг другу.
Пример 5. Проверка того, является ли данная матрица мультипликативной инверсией другой заданной матрицы
Являются ли матрицы
1234,⎛⎜⎜⎝1121314⎞⎟⎟⎠
мультипликативные инверсии друг друга?
Ответ
В этом примере нам нужно определить, являются ли две заданные матрицы обратными друг другу. Мы видим, что оба эти
матрицы являются матрицами 2×2. Напомним, что для матрицы 2 × 2 𝐴,
его мультипликативная обратная, обозначаемая 𝐴, является матрицей, которая удовлетворяет
𝐴𝐴=𝐴𝐴=𝐼,
если такая матрица существует. Напомним также, что 𝐼 — это единичная матрица размера 2 × 2.
1001. Если мы можем получить единичную матрицу
умножая матрицы в любом порядке, мы будем знать, что они мультипликативно обратны друг другу. Позволь нам
вычислить умножение матриц в указанном порядке. 1234⎛⎜⎜⎝1121314⎞⎟⎟⎠=⎛⎜⎜⎝1×1+2×131×12+2×143×1+4×133×12+4×14⎞⎟⎟⎠=⎛⎜⎜ ⎝53113352⎞⎟⎟⎠.
Мы видим, что полученная матрица не является единичной. Следовательно, две матрицы не являются мультипликативными обратными к
друг друга.
Ответ на вопрос в этом примере – нет.
В предыдущем примере мы проверяли, являются ли две заданные матрицы обратными друг другу. Используя этот метод, мы всегда можем
проверить, являются ли две заданные матрицы обратными друг другу. Однако это не лучший способ найти обратную матрицу.
так как нам нужно будет проверить это для каждой возможной матрицы. Введем формулу обратной
Матрица 2×2.
Формула: обратная матрица 2 × 2
Пусть 𝐴=𝑎𝑏𝑐𝑑 такая, что
дет𝐴≠0. Затем,
𝐴=1𝐴𝑑−𝑏−𝑐𝑎.det
Обратите внимание, что мы можем получить обратное из 𝐴 с помощью
- , поменяв местами 𝑎 и 𝑑,
902, 9003 и 𝑐 поменяв знаки 𝑐 и деление на определитель.
Докажем справедливость этой формулы, вычислив умножение матриц 𝐴𝐴. Матрица
умножение 𝐴𝐴 аналогично и опущено. У нас есть
𝐴𝐴 = m × 𝑎𝑐 × 𝑑+𝑑 × (−𝑐) 𝑐 × (−𝑏)+𝑑 × 𝑎 = 1𝐴𝑎𝑑 — 𝑏𝑐00𝑎𝑑 — 𝑏𝑐 = ⎛⎜⎜⎝𝑎𝑑 — 𝑏𝑐𝐴00𝑎𝑑 — 𝑏𝑐𝐴⎞⎟⎟⎠ = 1001. детдетдетдетдетдетдет
Действительно, умножение матрицы 𝐴 на матрицу 𝐴, как определено выше, приводит к тождеству
матрица 𝐼. Наряду с проверкой другого уравнения 𝐴𝐴=𝐼, которое
здесь опущены, мы доказали, что эта формула обращения к матрице справедлива.
Давайте на мгновение остановимся и зададим важный философский вопрос. Это единственная возможная матрица, обратная
𝐴? Другими словами, может ли матрица иметь обратную, не заданную этой формулой? Это вопрос, который относится к единственности обратной матрицы.
Давайте немного перефразируем этот вопрос. Мы уже знаем, что для невырожденной матрицы существует формула, определяющая
обратная матрица. Итак, наш вопрос, по сути, сводится к тому, могут ли две разные матрицы удовлетворять уравнениям
𝐴𝐴=𝐴𝐴=𝐼,
для заданной обратимой матрицы 𝐴. Мы покажем, что это невозможно. Скажите, что матрицы 𝐵
и 𝐶 обратны 𝐴. Тогда у нас должно быть
𝐴𝐵=𝐵𝐴=𝐼,𝐴𝐶=𝐶𝐴=𝐼.
В частности, это означает, что
𝐴𝐵=𝐴𝐶.
Мы можем умножить обе части уравнения слева на 𝐵, чтобы написать
𝐵𝐴𝐵=𝐵𝐴𝐶.
Поскольку 𝐵 является инверсией 𝐴, мы знаем, что 𝐵𝐴=𝐼, что дает нам
𝐼𝐵=𝐼𝐶.
𝐼 является мультипликативным тождеством, поэтому
𝐵=𝐶.
Это говорит нам о том, что 𝐵 и 𝐶 — одна и та же матрица. Это говорит нам о том, что если у нас есть какие-либо
две матрицы, обратные данной матрице, должны быть равны. Другими словами, существует только одна обратная сторона обратимого
матрица. Поскольку у нас есть формула для обратной матрицы 2 × 2, это должна быть единственная обратная матрица.
В следующем примере мы будем использовать эту формулу для вычисления обратной матрицы 2×2.
Пример 6. Нахождение обратной матрицы
Нахождение мультипликативной обратной матрицы
𝐴=−4−1035,
если возможно.
Ответ
В этом примере нам нужно найти обратную заданную матрицу 2×2, если это возможно. Напомним, что
обратная квадратная матрица существует (т. е. матрица обратима) тогда и только тогда, когда ее определитель не равен нулю. Мы видим, что порядок данной матрицы 2×2, что означает, что это квадратная матрица. Так,
нам нужно убедиться, что его определитель не равен нулю, чтобы гарантировать, что он обратим.
Напомним, что определитель матрицы 2×2 задается выражением
det𝑎𝑏𝑐𝑑=𝑎×𝑑−𝑏×𝑐.
Это приводит к
det𝐴=(−4)×5−(−10)×3=10.
Следовательно, определитель данной матрицы равен 10. Поскольку определитель отличен от нуля, мы знаем, что существует обратная матрица. Найдем обратное.
Напомним, что обратная матрица 𝐴=𝑎𝑏𝑐𝑑
с det𝐴≠0 определяется выражением
𝐴=1𝐴𝑑−𝑏−𝑐𝑎.det
Из 𝐴=−4−1035 видно, что
𝑎=−4, 𝑏=−10, 𝑐=3, 𝑑=5.
Мы также вычислили det𝐴=10. Подставив эти значения в формулу обратной матрицы, получим
𝐴=110510−3−4.
Вычисляя скалярное умножение, получаем
𝐴=⎛⎜⎜⎝5101010−310−410⎞⎟⎟⎠=⎛⎜⎜⎝121−310−25⎞⎟⎟⎠.
Теперь, когда мы знаем, как найти обратную матрицу 2×2, вернемся к проблеме, которая мотивировала это
разработка. Если мы знаем обратную матрицу, мы можем решить матричное уравнение
𝐴𝑋=𝐵
найти неизвестную матрицу 𝑋, где 𝐴 и 𝐵 известные матрицы. Чтобы решить эту
уравнения для неизвестной матрицы 𝑋, нам нужно слева от 𝐴𝑋 умножить на обратную матрицу
𝐴, если он существует. Поскольку это уравнение, мы должны сделать то же самое с правой частью уравнения. Этот
приводит к
𝐴𝐴𝑋=𝐴𝐵.
Мы знаем 𝐴𝐴=𝐼, что является единичной матрицей. Это ведет к
𝑋=𝐴𝐵.
Как: Решение матричных уравнений
Пусть 𝐴 — обратимая матрица, а 𝐴 и 𝐵 —
Матрицы 2×2. Матрица 𝑋, удовлетворяющая уравнению 𝐴𝑋=𝐵, есть
𝑋=𝐴𝐵.
Аналогично, матрица 𝑋, удовлетворяющая уравнению 𝑋𝐴=𝐵,
𝑋=𝐵𝐴.
Мы видим, что решение уравнения 𝐴𝑋=𝐵 отличается от решения 𝑋𝐴=𝐵
потому что умножение матриц некоммутативно. В любом случае нам нужно умножить обе части уравнения на обратное
𝐴, но имеет значение, с какой стороны мы умножаем.
В нашем последнем примере мы применим наши знания об обратной матрице, чтобы решить матричное уравнение, включающее
Матрицы 2×2.
Пример 7. Решение матричных уравнений
Используя обратные матрицы, решите следующее для 𝑋:
𝑋−324−3=0−230.
Ответ
В этом примере нам нужно решить матричное уравнение. Напомним, что мы можем решить матричное уравнение вида
𝐴𝑋=𝐵 или 𝑋𝐴=𝐵 с помощью обратной матрицы 𝐴, если она существует. В этом примере матрица 𝐴 — это матрица в левой части уравнения
𝐴=−324−3.
Сначала проверим, существует ли обратная этой матрицы. Напомним, что существует обратная квадратная матрица (т.е. матрица
обратим) тогда и только тогда, когда его определитель не равен нулю. Мы видим, что порядок матрицы 𝐴 равен
2×2, что означает, что это квадратная матрица. Итак, нам нужно убедиться, что его определитель не равен
к нулю, чтобы убедиться, что оно обратимо.
Напомним, что определитель матрицы 2×2 задается выражением
det𝑎𝑏𝑐𝑑=𝑎×𝑑−𝑏×𝑐.
Это приводит к
det𝐴=(−3)×(−3)−2×4=1.
Следовательно, определитель данной матрицы равен 1. Поскольку определитель отличен от нуля, мы знаем, что существует обратная матрица. Найдем обратное.
Напомним, что обратная матрица 𝐴=𝑎𝑏𝑐𝑑
с det𝐴≠0 определяется выражением
𝐴=1𝐴𝑑−𝑏−𝑐𝑎.det
Из 𝐴=−324−3 видно, что
𝑎=−3,𝑏=2,𝑐=4,𝑑=−3.
Мы также знаем, что det𝐴=1, что означает, что скалярный множитель 1𝐴det в
формулой можно пренебречь. Подставив эти значения в формулу обратной матрицы, получим
𝐴=−3−2−4−3.
Теперь, когда мы вычислили обратную матрицу, давайте рассмотрим, как решить уравнение. Обозначая матрицу справа
часть уравнения как 𝐵, наше уравнение имеет вид
𝑋𝐴=𝐵.
Мы можем умножить 𝐴 справа на обе части уравнения, чтобы написать
𝑋𝐴𝐴=𝐵𝐴.
Мы знаем, что 𝐴𝐴=𝐼, что является единичной матрицей. Поскольку умножение на единичную матрицу не
меняем матрицу, имеем
𝑋=𝐵𝐴.
Следовательно, нам нужно найти умножение матриц 𝐵𝐴:
𝐵𝐴=0−230−3−2−4−3=0×(−3)+(−2)×(−4)0×(−2)+(−2)×(−3 )3×(−3)+0×(−4)3×(−2)+0×(−3)=86−9−6.
Следовательно, ответ
𝑋=86−9−6.
Давайте закончим повторением нескольких важных понятий из объяснения.
Ключевые моменты
- Пусть 𝐴 — матрица 2×2. Обратное к 𝐴, обозначаемое
𝐴 — матрица, удовлетворяющая
𝐴𝐴=𝐼,𝐴𝐴=𝐼.
Если такая матрица существует, мы говорим, что матрица 𝐴 обратима. Если такой матрицы не существует, говорят
что матрица 𝐴 необратима. - Пусть 𝐴 — обратимая матрица. Тогда 𝐴 обратимо и
𝐴=𝐴. - Сингулярная матрица — это квадратная матрица, определитель которой равен нулю. Квадратная матрица необратима, если и
только если он единичный. - Пусть 𝐴=𝑎𝑏𝑐𝑑 такое, что
дет𝐴≠0. Затем,
𝐴=1𝐴𝑑−𝑏−𝑐𝑎.det - Пусть 𝐴 — обратимая матрица, а 𝐴 и 𝐵 —
Матрицы 2×2.Матрица 𝑋, удовлетворяющая уравнению 𝐴𝑋=𝐵, есть
𝑋=𝐴𝐵.
Аналогично, матрица 𝑋, удовлетворяющая уравнению 𝑋𝐴=𝐵, равна
𝑋=𝐵𝐴.
линейная алгебра — равенство Якоби между дополнительными минорами обратных матриц
По этому вопросу сказано не все, что стоит сказать — в
по крайней мере, кто-то мог записать версию без
абсолютные значения; но, что более важно, есть множество других столь же хороших доказательств.
Позвольте мне сначала сформулировать результат с правильными знаками и без абсолютных значений.
Постоянные предположения. В этом посте будут использоваться следующие обозначения:
-
Пусть $mathbb{K}$ — коммутативное кольцо. Все матрицы, которые появляются в
ниже приведены матрицы над $mathbb{K}$. -
Пусть $mathbb{N}=left{ 0,1,2,ldotsright} $.
-
Для каждого $ninmathbb{N}$ обозначим через $left[ nright] $ множество
$влево{ 1,2,ldots,nвправо} $. -
Исправить $ninmathbb{N}$.
-
Пусть $S_n$ обозначает $n$-ю симметрическую группу (т.е. группу
перестановки $left[ nright] $). 9{ широкая тильда {J}} справа) .
конец{выравнивание}Вот три ссылки на доказательства теоремы 1:
-
Теорема 1 — лемма A.1 (e) в Sergio Caracciolo, Alan D. Sokal, Andrea
Sportiello, Алгебраические/комбинаторные доказательства тождеств типа Кэли для
производные определителей и пфаффианы , arXiv:1105.6270v2 (опубликовано в:
Успехи прикладной математики 50, 474–594 (2013)). В пункте
Следуя теореме A.16, доказательство дается с использованием того, что авторы называют
«интеграция Грассмана-Березина» (несмотря на название, чисто алгебраическая
фиктивное исчисление снаружи
алгебра векторного пространства). -
Теорема 1 есть (1) у Пьера Лалонда, Некоммутативная версия теоремы Якоби.
равенство кофакторов матрицы , Дискретная математика 158 (1996), стр.{sum I+sum J}$ занимает очень много места, хотя его так легко
убедите себя в этом, взмахнув рукой, чтобы не заметить, что это
требует вообще каких-либо доказательств. Второе доказательство является расширением аргумента
кратко изложено в
Д. Лаксов, А. Ласко, П. Прагач и А. Торуп, 9{ широкая тильда {J}} справа) $
для некоторого значения $pm$. Но это более слабое утверждение не так полезно, как
Теорема 1 в ее полной версии (в частности, недостаточно было бы
заполнить пробел в книге Макдональда, который побудил задать этот вопрос).Перестановка $wleft( Kright) $
Сначала введем еще несколько обозначений:
Если $K$ является подмножеством $left[ nright] $, и если $k = влево|Квправо|$,
тогда пусть $wleft( Kright) $
— (единственная) перестановка $sigmain S_n$, первые $k$ значений которой
$sigmaleft( 1right),sigmaleft( 2right),ldots,sigmaleft(
kright) $ — элементы $K$ в порядке возрастания, следующие $n-k$ которых
значения $sigmaleft(k+1right),sigmaleft(k+2right),ldots
,sigmaleft( nright) $ — элементы $widetilde{K}$ в порядке возрастания.9{ сумма K- влево ( 1 + 2 + cdots + влево | K вправо | вправо)} $.
Вам не нужно доказывать лемму 2, если вас интересуют только более слабые
вариант теоремы 1 со знаком $pm$.Доказательство леммы 2. Пусть $k=left| Кправо| $. Пусть $a_{1},a_{2}
,ldots,a_{k}$ — $k$ элементов $K$ в порядке возрастания (без
повторы). Пусть $b_{1},b_{2},ldots,b_{n-k}$ — $n-k$ элементов
$widetilde{K}$ в порядке возрастания (без повторений). Пусть $gamma
=wвлево( Kвправо) $. Тогда определение $wleft(Kright) $ показывает
что первые значения $k$ $gammaleft( 1right) ,gammaleft( 2right)
,ldots,gammaleft( kright) $ $gamma$ — это элементы $K$ в
порядке возрастания (то есть $a_{1},a_{2},ldots,a_{k}$), а следующие $n-k$
значения $gammaleft(k+1right),gammaleft(k+2right),ldots
,gammaleft( nright) $ $gamma$ — элементы $widetilde{K}$ в
порядке возрастания (то есть $b_{1},b_{2},ldots,b_{n-k}$). Другими словами,
начать{выравнивать}
влево(гаммавлево(1вправо),гаммавлево(2вправо),ldots
,gammaleft( nright) right) =left( a_{1},a_{2},ldots,a_{k}
,b_{1},b_{2},ldots,b_{n-k}right) .
end{выравнивание}Теперь вы можете получить список $left( gammaleft( 1right) ,gammaleft(
2right) ,ldots,gammaleft( nright) right) $ из списка $left(
1,2,ldots,nright) $, последовательно переключая соседние элементы следующим образом:-
Сначала переместите элемент $a_{1}$ в начало списка, последовательно
переключая его с каждой из записей $a_{1}-1$ меньше него. -
Затем переместите элемент $a_{2}$ на вторую позицию, последовательно
переключение с каждой из записей $a_{2}-2$ (кроме $a_{1}$) меньшего размера
чем это. -
Затем переместите элемент $a_{3}$ на третью позицию последовательно
переключая его с каждой из записей $a_{3}-3$ (кроме $a_{1}$ и
$a_{2}$) меньше его. -
И так далее, пока вы, наконец, не переместите элемент $a_{k}$ на $k$-ю позицию.
Более формально, вы перебираете все $iinleft{ 1,2,ldots,kright}
$ (в порядке возрастания), каждый раз перемещая элемент $a_{i}$ на $i$-й
положение в списке, последовательно переключая его с помощью каждого из $a_{i}-i$
записи (кроме $a_{1},a_{2},ldots,a_{i-1}$) меньше его.В конце первые $k$ позиции списка заполняются $a_{1}
,a_{2},ldots,a_{k}$ (именно в таком порядке), а остальные $n-k$ позиций
заполняются оставшимися элементами $b_{1},b_{2},ldots,b_{n-k}$ (опять же, в
этот порядок, потому что переключатели никогда не нарушали их
строго возрастающий относительный порядок). Таким образом, в конце ваш список точно
$left( a_{1},a_{2},ldots,a_{k},b_{1},b_{2},ldots,b_{n-k}right) =left(
gammaleft( 1right) ,gammaleft( 2right) ,ldots,gammaleft(
псправа) справа) $. Всего вы использовали
начать{выравнивать}
& влево( a_{1}-1вправо) +влево( a_{2}-2вправо) +cdots+влево(
a_{k}-kсправа) \
& = underbrace{ left( a_ {1} + a_ {2} + cdots + a_ {k} right)} _ { substack {= sum
K\text{(по определению }a_{1},a_{2},ldots,a_{k}text{)}
}}-underbrace{left( 1+2+cdots+kright)}_{substack{=1+2+cdots
+влево| Кправо| \text{(так как }k=left| Kright| text{)}}} \
& =sum K-left( 1+2+cdots+left| Kright| right)
end{выравнивание}
переключатели.{n}right) $. 9{ сумма K- влево ( 1 + 2 + cdots + влево | K вправо | вправо)} e _ { влево [ п вправо] } .
конец{выравнивание}Доказательство леммы 4. Пусть $k = left|Kright|$.
Пусть $sigma$ — перестановка $wleft( Kright) in
S_n$ определено выше. Его первые $k$ значений $sigmaleft( 1right)
,sigmaleft( 2right) ,ldots,sigmaleft( kright) $ — элементы
$K$ в порядке возрастания; таким образом, $ e _ { sigma влево ( 1 вправо)} клин
e _ { сигма влево ( 2 вправо)} клин cdots клин e _ { сигма влево ( k вправо)
}=e_K$. Его следующие $n-k$ значений $sigmaleft( k+1right) ,sigmaleft(
k+2right) ,ldots,sigmaleft( nright) $ — элементы
$widetilde{K}$ в порядке возрастания; таким образом, $e_{sigmaleft(k+1right)
} клин e _ { sigma влево ( k + 2 вправо) } клин cdots клин e _ { sigma влево (
nright) }=e_{widetilde{K}}$. 9{ сигма} е _ { влево [п вправо]}
& = е _ { сигма влево ( 1 вправо)
} клин е _ { сигма влево ( 2 вправо) } клин cdots клин е _ { сигма влево (
псправа) } \
& знак равно underbrace { влево ( e _ { sigma влево ( 1 вправо) } клин e _ { sigma влево (
2 справа)} клин cdots клин e _ { сигма влево (k вправо)} вправо)} _ {= e_K
} underbrace { left ( e _ { sigma left ( k + 1 right) } клин e _ { sigma left (
k + 2 справа)} клин cdots клин e _ { сигма влево ( п вправо)} вправо)
}_{=e_{widetilde{K}}} \
& = e_K e_{widetilde{K}} .{сумма К-влево( 1+2+cdots+влево|Квправо|вправо)
} e _ { left [ n right]} = e_K e _ { widetilde {K}} $. Это доказывает лемму 4.
$черный квадрат$ 9{K}right) e_{left[nright]} .
конец{выравнивание}Доказательство следствия 5. Пусть $K in mathcal{P}_{k}left( left[ nright] right) $.
Пусть $Iinmathcal{P}_{k}left( left[ nright]
right) $ таков, что $Ineq K$. Тогда $Inot subseteq K$ (поскольку множества
$I$ и $K$ имеют одинаковый размер $k$). Следовательно, существует некоторый $zin I$, такой
что $znotin K$. Рассмотрим это $z$. У нас есть $zin I$ и $zinwidetilde{K}$
(так как $znotin K$). Следовательно, и $e_{I}$, и $e_{widetilde{K}}$ являются «клиновидными».
произведения», содержащие множитель $e_{z}$, поэтому произведение $e_{I}
e_{widetilde{K}}$ — это «клинообразный продукт», дважды содержащий этот множитель. Таким образом,
$e_{I}e_{widetilde{K}}=0$. 9{ widetilde {J}} right) e _ { left [n right]
} .
label{darij1.eq6}
тег{6}
end{выравнивание}
Но
начать{выравнивать}
& kleft( nkright) +underbrace{sumwidetilde{J}}_{=sumleft{
1,2,ldots,nright} -sum J}-underbrace{left( 1+2+cdots+left(
n-kright) right) }_{=sumleft{ 1,2,ldots,n-kright} } \
& = kleft( n-kright) +sumleft{ 1,2,ldots,nright} -sum
J-sumleft{ 1,2,ldots,n-kright} \
& = underbrace{sumleft{ 1,2,ldots,nright} -sumleft{ 1,2,ldots
,nkright} _{substack{=sumleft{nk+1,nk+2,ldots,nright}
\=kleft( n-kright) +sumleft{ 1,2,ldots,kright} \=kleft(
n-kright) +left( 1+2+cdots+kright) }}+kleft( n-kright) -sum J \
& = 2kleft( n-kright) +left( 1+2+cdots+kright) -sum J \
& equiv-left( 1+2+cdots+kright) -sum J mod 2 .{–1}$, так что умножение матрицы на обратную дает единичную матрицу $I$ .
В этом уроке мы рассмотрим, что такое обратная матрица, как найти обратную матрицу, формулу обратной матрицы $2times 2$ и $3times 3$ матрица и примеры, поясняющие наше понимание обратных матриц.
Что такое обратная матрица?
Помните мультипликативное обратное число?
Например, возьмем число $8$. На какое число мы можем умножить $8$, чтобы получить $1$?
Просто!
Это обратное от $ 8 $, что равно $ frac { 1 }{ 8 } $!
$ 8 times frac{1}{8} = 1 $
Точно так же в матричной алгебре матрица , обратная , играет ту же роль, что и обратная величина в системах счисления. Обратная матрица — это матрица, на которую мы можем умножить другую матрицу, чтобы получить единичную матрицу (матричный эквивалент числа $1$) ! Чтобы узнать больше о матрице идентичности, пожалуйста, проверьте здесь.
9{– 1} $.
Мультипликативная обратная (обратная) в системе счисления и обратная матрица в матрицах играют одну и ту же роль. Кроме того, единичная матрица ($I$) (в области матриц) играет ту же роль, что и число один ($1$).
Как найти обратную матрицу
Так как же найти обратную матрицу?
Чтобы найти обратную матрицу, мы можем использовать формулу, которая требует выполнения нескольких пунктов перед ее использованием.
У каждой ли матрицы есть обратная?
Ну НЕТ!
Чтобы матрица имела обратную, она должна удовлетворять $ 2 $ условиям:
- Матрица должна быть квадратной матрицей (количество строк должно быть равно количеству столбцов).
- Определитель матрицы (это скалярное значение матрицы из нескольких операций над ее элементами) не должен быть равен $0$.
Помните, что не все квадратные матрицы имеют обратную.
Матрица, определитель которой равен $0$, не равна обратимая (не имеет обратной) и известна как сингулярная матрица .
Подробнее об определителях и сингулярных матрицах!
Мы рассмотрим изящную формулу для нахождения обратной матрицы $ 2 times 2 $ ниже. Кроме того, формула для матрицы $ 3 x 3 $ будет настоящей беспорядочной ! Будьте готовы! 🙂
Помните,
Мы можем вычислить только обратное для квадратных матриц! Также определитель матрицы не может быть равным $ 0 $, так как формула требует деления на определитель. Мы знаем, что деление на $0$ равно undefined!
Формула обратной матрицы
В этом разделе мы найдем обратную матрицу $ 2 times 2 $ и $ 3 times 3 $.
Обратная матрица 2 x 2
Рассмотрим матрицу $ 2 times 2 $, показанную ниже:
$ A = begin{bmatrix} { a } & { b } \ { c } & { d } конец {bmatrix} $ 9{ – 1 } = frac{ 1 }{ad – bc} begin{bmatrix} d & { – b } \ { – c } & a end {bmatrix} $
Количество $ ad – bc $ известен как определитель матрицы.
Вычислим обратную матрицу $ 2 times 2 $ ( Matrix $ B $ ), показанную ниже:
$ B = begin{bmatrix} 1 & 3 \ – 3 & 2 end {bmatrix} $
На самом деле это квадратная матрица, и давайте сначала проверим, равен ли определитель $0$ или нет. Вычислим определитель: 9{ – 1 } = begin{bmatrix} { frac {2} {11}} & { – frac {3} {11} } \ { frac { 3 }{11}} & { frac {1 }{11} } end {bmatrix} $
Примечание: На последнем шаге мы умножили скалярную константу $ frac{1}{11} $ на каждый элемент матрицы. Это скалярное умножение матрицы.
Обратная матрица 3 x 3
Рассмотрим матрицу $ 3 times 3 $, показанную ниже: & я end {bmatrix} $ 9{ – 1 } = frac{1}{ det(B)} begin{bmatrix} { (ei – fh) } & { – (bi – ch) } & {(bf – ce)} \ { – ( di- fg) } & { (ai – cg)} & { – (af – cd)} \ { (dh – eg)} & { – (ah – bg)} & {(ae – bd)} end {bmatrix} $
Где $ det( B ) $ — определитель матрицы $ 3times 3 $, заданной как:
$ det(B) = a(ei – fh) – b(di – fg) + c(dh – например) $
Ого! Действительно грязный!
Но тем не менее, давайте вычислим обратную матрицу $ 3 times 3 $ ( Матрица $ B $ ), показанную ниже:
$ B = begin{bmatrix} { 1 } & { 2 } & { – 1 } \ { 0 } & { 3 } & { – 4 } \ { – 1 } & { 2 } & { 1 } end {bmatrix} $
На самом деле это квадратная матрица, и давайте сначала проверим, равен ли определитель $ 0 $ или нет.
Вычислим определитель:
$ det( B ) = | Б | = 1 [ ( 3 )( 1 ) – ( – 4 )( 2 ) ] – 2 [ ( 0 )( 1 ) – ( – 4 )( – 1 ) ] + (-1) [ ( 0 )( 2 ) – ( 3 )( – 1 ) ] $
$ = 1 [ 3 + 8 ] – 2 [ 0 – 4 ] + (-1) [ 0 + 3 ] $
$ = 1 [ 11 ] – 2[ – 4 ] – 1[ 3 ] $ 9{ – 1 } = begin{bmatrix} { frac{ 11 }{ 16 } } & { – frac{1}{4} } & { – frac{5}{16} } \ { frac{ 1 }{ 4 } } & { 0 } & { frac{1}{4} } \ { frac{3 }{16} } & { – frac{1}{4} } & { frac{ 3 }{ 16 } } end {bmatrix} $Примечание: На последнем шаге мы умножили скалярную константу $ frac{ 1 }{ 16 } $ на каждый элемент матрицы. Это скалярное умножение матрицы.
Давайте посмотрим на пару примеров! 9{ – 1 } = begin{bmatrix} frac{1}{7} & – frac{2}{7} \ -frac{3}{7} & – frac{1}{7} end {bmatrix} $
Пример 2Дано $ A= begin{bmatrix} 0 & -2 \ -1 & 1 end {bmatrix} $ и $ B= begin{bmatrix} -frac{1}{2} & -1 \ -frac{1}{2} & 0 end {bmatrix}$, подтвердите, является ли матрица $B$ обратной матрице $A$.
Решение
Чтобы матрица $B$ была обратной матрице $A$, умножение этих двух матриц должно дать единичную матрицу. Если это так, то $B$ является инверсией $A$. Проверим:
$ Atimes B= begin{bmatrix} 0 & -2 \ -1 & 1 end {bmatrix} times begin{bmatrix} -frac{1}{2} & -1 \ — frac{1}{2} & 0 end {bmatrix} $
$ = begin{bmatrix} (0)(-frac{1}{2}) + (-2)(-frac{1 {2}) & (0)(-1) + (-2)(0) \ (-1)(-frac{1}{2}) + (1)(-frac{1}{ 2}) & (-1)(-1) + (1)(0) end {bmatrix} $
$ = begin{bmatrix} 1 & 0 \ 0 & 1 end {bmatrix} $
Это тождественная матрица.
Таким образом, матрица $B$ является обратной матрице $A$. 9{ – 1 } = begin{bmatrix} frac{1}{11} & -frac{1}{33} \ frac{2}{33} & frac{1}{11} end { bmatrix} $ -
- Это квадратная матрица размером $ 3 x 3 $. Вычислим определитель этой матрицы.
Если у нас есть $ 3 times 3 $ матрица $ A = begin{bmatrix} a & b & c \ d & e & f \ g & h & i end {bmatrix} $,
определитель есть $det(A) = a(ei – fh) – b(di – fg) + c(dh – eg) $.
Теперь вычисляем определитель нашей матрицы $B$:
$ det(B) = a(ei – fh) – b(di – fg) + c(dh – eg) $
$ det(B) = 1(20+2) – 6(10-1) + 4(4+4) $
$ det(B) = 1(22) – 6(9) + 4(8) $
$ det(B) = 1(20+2) – 6(10-1) + 4(4+4) $
$det(B) = 0$Поскольку определитель равен $ 0 $, мы не можем вычислить обратную матрицу $B$. Таким образом, эта матрица не имеет обратной!
Предыдущий урок | Главная страница | Следующий урок
Х. Д. Икрамов, “О сравнительном значении коэффициентов роста Гаусса для взаимно обратных матриц”, Ж. вычисл. Вычисл. Мат. Мат. физ., 25:1 (1985), 134–136; вычисл. Мат. Мат. Phys., 25:1 (1985), 87–89
Журнал вычислительной математики и математической физики
РУС
РУСЖУРНАЛЫ
ЛЮДИ
ОРГАНИЗАЦИИ
КОНФЕРЕНЦИИ
СЕМИНАРЫ
ВИДЕО БИБЛИОТЕКА
ПАКЕТ AMSBIBВ вашем браузере отключен JavaScript.
Включите его, чтобы включить полную функциональность веб-сайта
Общая информация Последний выпуск Архив Импакт-фактор Поисковые документы Поиск ссылок RSS Последний выпуск Текущие выпуски Проблемы с архивом Что такое RSS
Личный кабинет: Логин: Пароль: Сохранить пароль Введите Забыли пароль? Регистр
Ж. Вычисл. Мат. Мат. физ., 1985, том 25, номер 1, страницы 134–136
(ми звммф4258)
Научная связь
О сравнительном значении коэффициентов роста Гаусса для взаимно обратных матриц
Х. Д. Икрамов
Москва
Загрузить полный текст в формате PDF (337 КБ)
Поступила в редакцию: 29.07.1983
Английская версия:
Вычислительная математика и математическая физика, 1985, 25 :1, 87–89
Библиографические базы данных:
Тип документа:
АртикулУДК:
519.613MSC: 65F05
Язык: Русский
Ссылка:
Х. Д. Икрамов, “О сравнительном значении коэффициентов роста Гаусса для взаимно обратных матриц”, Ж. вычисл. Вычисл.No related posts.
-
Присоединённая (союзная, взаимная) матрица — матрица [math]displaystyle{ {C}^{*} }[/math], составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы.
Из определения следует, что присоединённая матрица рассматривается только для квадратных матриц и сама является квадратной, так как понятие алгебраического дополнения вводится для квадратных матриц.
[math]displaystyle{ {C}^{*}= begin{pmatrix}
{A}_{11} & {A}_{21} & cdots & {A}_{n1} \
{A}_{12} & {A}_{22} & cdots & {A}_{n2} \
vdots & vdots & ddots & vdots \
{A}_{1n} & {A}_{2n} & cdots & {A}_{nn} \
end{pmatrix} }[/math]
Исходная матрица:
[math]displaystyle{ {A}= begin{pmatrix}
{a}_{11} & {a}_{12} & cdots & {a}_{1n} \
{a}_{21} & {a}_{22} & cdots & {a}_{2n} \
vdots & vdots & ddots & vdots \
{a}_{n1} & {a}_{n2} & cdots & {a}_{nn} \
end{pmatrix} }[/math]
Где:
- [math]displaystyle{ {C}^{*} }[/math] — присоединённая (союзная, взаимная) матрица;
- [math]displaystyle{ {A}_{ij} }[/math] — алгебраические дополнения исходной матрицы;
- [math]displaystyle{ {a}_{ij} }[/math] — элементы исходной матрицы.
Эта матрица нужна для вычисления обратной матрицы:
- [math]displaystyle{
{A}^{-1}= {{{C}^{*}}over{det(A)}}
}[/math]
где [math]displaystyle{ det(A) }[/math] — определитель матрицы [math]displaystyle{ A }[/math].
Обозначение
- [math]displaystyle{ {C}^{*} }[/math]
- [math]displaystyle{ {C}^{c} }[/math]
- [math]displaystyle{ {C}^{v} }[/math]
- [math]displaystyle{ operatorname{adj}A }[/math]
См. также
- Обратная матрица
- Алгебраическое дополнение
- Линейная алгебра
Литература
- Гантмахер Ф. Р. Теория матриц. — 2-е изд. — М.: Наука, 1966.








 Хочу понять, почему у меня не получается осуществить преобразования Лоренца для тензора электромагнитного поля.
Хочу понять, почему у меня не получается осуществить преобразования Лоренца для тензора электромагнитного поля.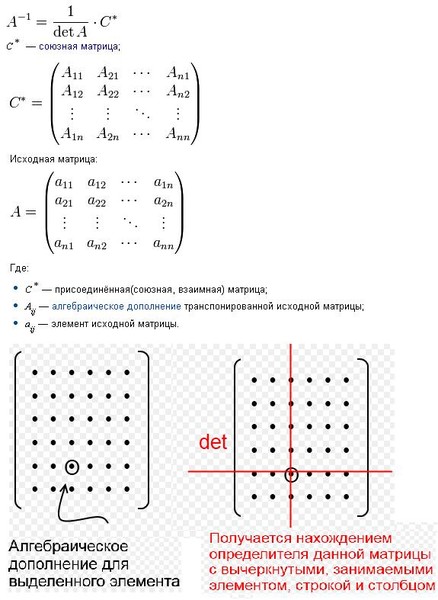
 physics в сообщении #1256227 писал(а):
physics в сообщении #1256227 писал(а):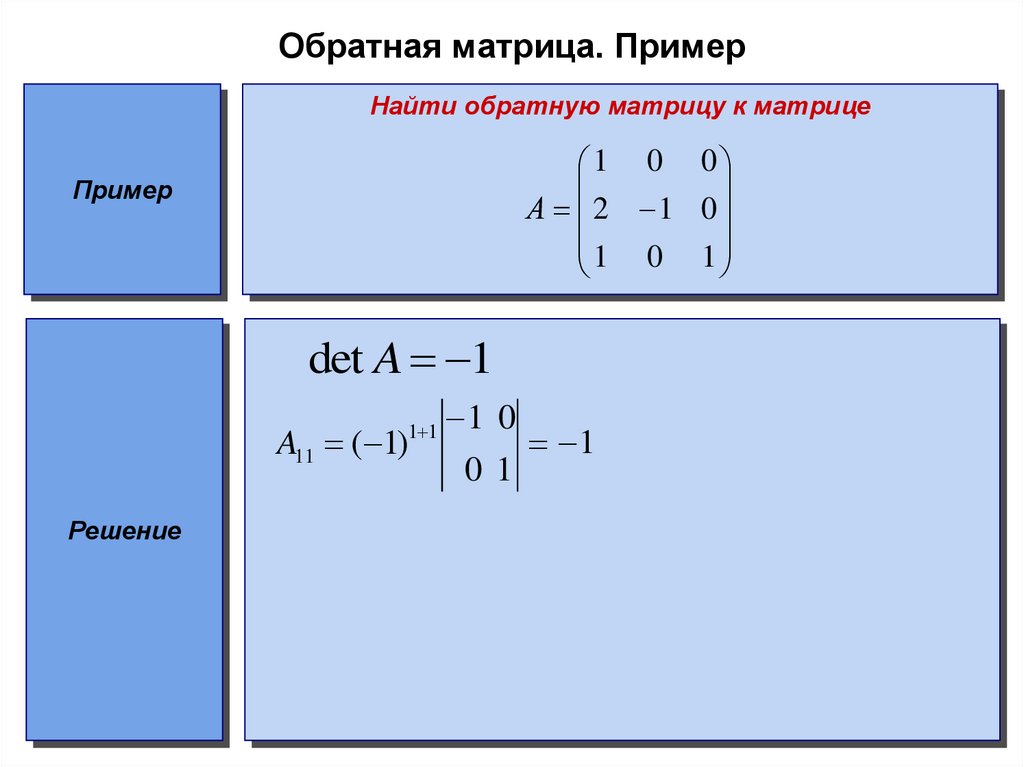
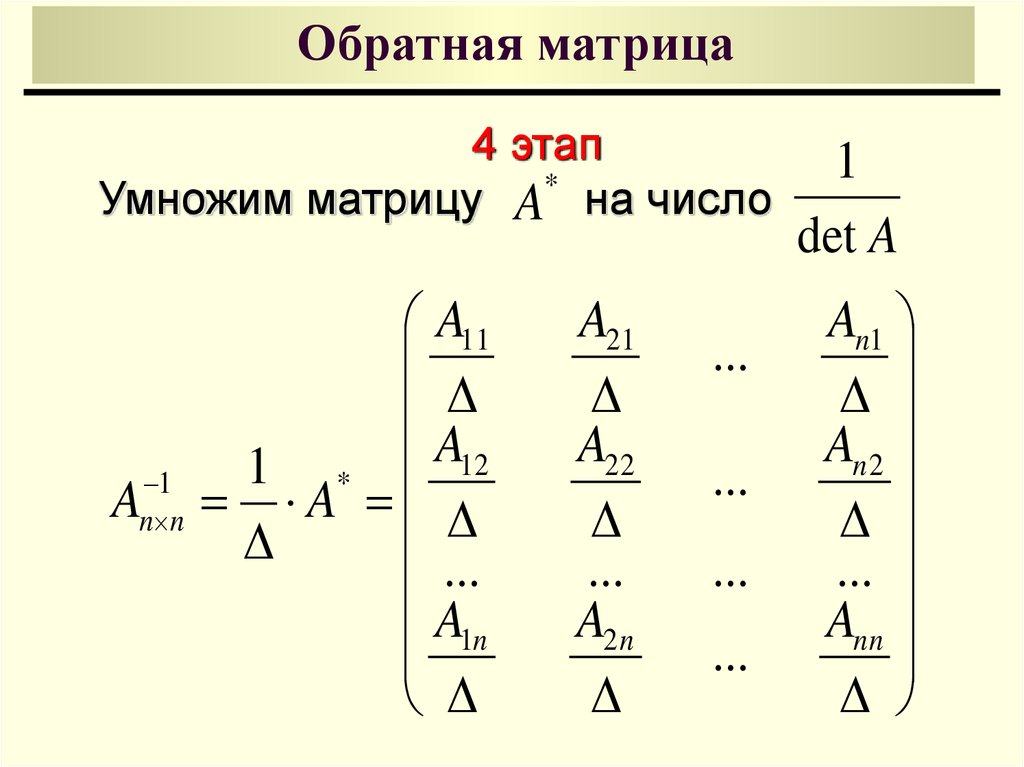 Да, согласен у матриц преобразований индексы не свернуты, возле них есть еще один тензор. Просто меня удивило когда я считал, например то получил тот же . Вот я и подумал что взаимная обратность матриц проникает сюда. Но все-таки где-то я ошибаюсь.
Да, согласен у матриц преобразований индексы не свернуты, возле них есть еще один тензор. Просто меня удивило когда я считал, например то получил тот же . Вот я и подумал что взаимная обратность матриц проникает сюда. Но все-таки где-то я ошибаюсь. physics в сообщении #1256247 писал(а):
physics в сообщении #1256247 писал(а):
 Преобразование тензора электромагнитного поля.
Преобразование тензора электромагнитного поля. Честно, аккуратно и правило едино для всех — и -объектов. Потом тупо вычисляете 16 чисел для . Здесь важно именно «просто набор чисел». А потом также аккуратно, по вашему же правилу, компонуете этот сброд из 16-ти чисел в любимую вами матрицу. Так вот, какое бы правило компоновки вы не сочините, если все сделаете аккуратно, всегда будете получать только правильный ответ и тензор у вас будет меняться, как положено. А теперь коротко: тензор — это элемент векторного пространства, закон преобразования его компонент — линейный и не важно каким способом вы будете организовывать его в таблички, треугольники, строчки , столбцы, колонки парами , красить цветом и т.д.
Честно, аккуратно и правило едино для всех — и -объектов. Потом тупо вычисляете 16 чисел для . Здесь важно именно «просто набор чисел». А потом также аккуратно, по вашему же правилу, компонуете этот сброд из 16-ти чисел в любимую вами матрицу. Так вот, какое бы правило компоновки вы не сочините, если все сделаете аккуратно, всегда будете получать только правильный ответ и тензор у вас будет меняться, как положено. А теперь коротко: тензор — это элемент векторного пространства, закон преобразования его компонент — линейный и не важно каким способом вы будете организовывать его в таблички, треугольники, строчки , столбцы, колонки парами , красить цветом и т.д. Преобразование тензора электромагнитного поля.
Преобразование тензора электромагнитного поля. Преобразование тензора электромагнитного поля.
Преобразование тензора электромагнитного поля.
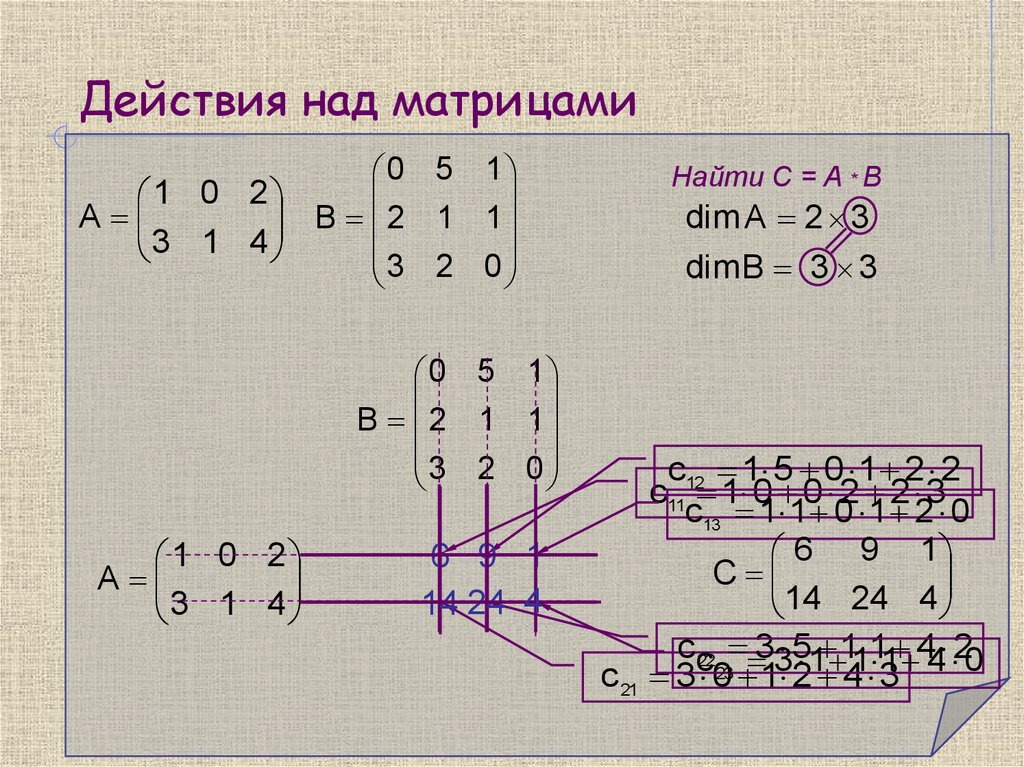 Преобразование тензора электромагнитного поля.
Преобразование тензора электромагнитного поля. А потом по той же формуле (1) посчитать как изменяется тензор поля… Надо будет как-то сделать на досуге.
А потом по той же формуле (1) посчитать как изменяется тензор поля… Надо будет как-то сделать на досуге. Соответствующие формулы выписываются в литературе не так повсеместно, как те, которые Вы перепроверяли. А уж преобразование компонент поля для этого случая я, кажется, нигде не видел в книгах.
Соответствующие формулы выписываются в литературе не так повсеместно, как те, которые Вы перепроверяли. А уж преобразование компонент поля для этого случая я, кажется, нигде не видел в книгах.