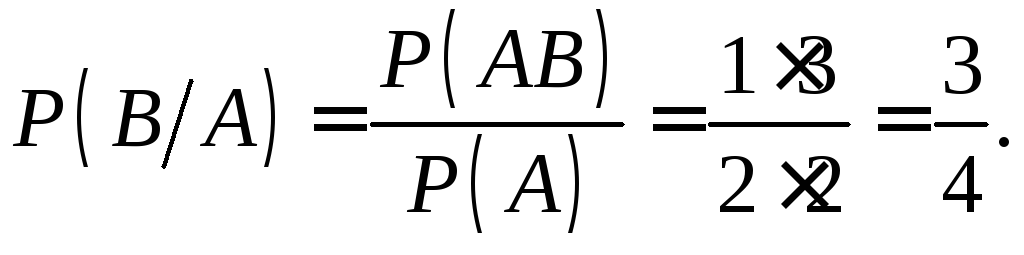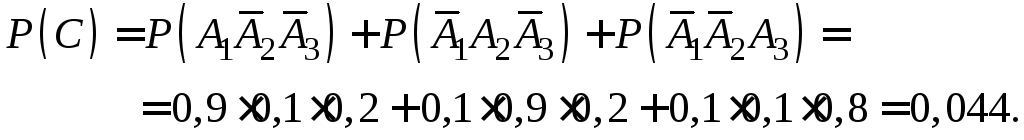X с чертой сверху как найти

Описательные статистики

Среднее арифметическое

Медиана

Мода

Среднее геометрическое

Взвешенное среднее

Размах (интервал изменения)

Размах, полученный из процентилей

Что такое процентили

Применение процентилей

Дисперсия

Cреднеквадратическое отклонение, стандартное отклонение выборки

Вариация в пределах субъектов и между субъектами

Пусть Х₁, Х₂ … X_n — выборка независимых случайных величин.

Упорядочим эти величины по возрастанию, иными словами, построим вариационный ряд:

Х₍₁₎ < Х₍₂₎ < … < X _(n) ,   (*)

где Х₍₁₎ = min ( Х₁, Х₂ … X_n),

Х_(n) = max ( Х₁, Х₂ … X_n).

Элементы вариационного ряда (*) называются порядковыми статистиками.

Величины d_(i) = X_(i+1) — X_(i) называются спейсингами или расстояниями между порядковыми статистиками.

Размахом выборки называется величина

R = X_(n) — X₍₁₎

Иными словами, размах это расстояние между максимальным и минимальным членом вариационного ряда.

Выборочное среднее равно: = (Х₁ + Х₂ + … + X_n) / n

Среднее арифметическое

Вероятно, большинство из вас использовало такую важную описательную статистику, как среднее.

Среднее — очень информативная мера «центрального положения» наблюдаемой переменной, особенно если сообщается ее доверительный интервал. Исследователю нужны такие статистики, которые позволяют сделать вывод относительно популяции в целом. Одной из таких статистик является среднее.

Доверительный интервал для среднего представляет интервал значений вокруг оценки, где с данным уровнем доверия, находится «истинное» (неизвестное) среднее популяции.

Например, если среднее выборки равно 23, а нижняя и верхняя границы доверительного интервала с уровнем p=.95 равны 19 и 27 соответственно, то можно заключить, что с вероятностью 95% интервал с границами 19 и 27 накрывает среднее популяции.

Если вы установите больший уровень доверия, то интервал станет шире, поэтому возрастает вероятность, с которой он «накрывает» неизвестное среднее популяции, и наоборот.

Хорошо известно, например, что чем «неопределенней» прогноз погоды (т.е. шире доверительный интервал), тем вероятнее он будет верным. Заметим, что ширина доверительного интервала зависит от объема или размера выборки, а также от разброса (изменчивости) данных. Увеличение размера выборки делает оценку среднего более надежной. Увеличение разброса наблюдаемых значений уменьшает надежность оценки.

Вычисление доверительных интервалов основывается на предположении нормальности наблюдаемых величин. Если это предположение не выполнено, то оценка может оказаться плохой, особенно для малых выборок.

При увеличении объема выборки, скажем, до 100 или более, качество оценки улучшается и без предположения нормальности выборки.

Довольно трудно «ощутить» числовые измерения, пока данные не будут содержательно обобщены. Диаграмма часто полезна в качестве отправной точки. Мы можем также сжать информацию, используя важные характеристики данных. В частности, если бы мы знали, из чего состоит представленная величина, или если бы мы знали, насколько широко рассеяны наблюдения, то мы бы смогли сформировать образ этих данных.

Среднее арифметическое, которое очень часто называют просто «среднее», получают путем сложения всех значений и деления этой суммы на число значений в наборе.

Это можно показать с помощью алгебраической формулы. Набор n наблюдений переменной X можно изобразить как X₁, X₂, X₃, …, X_n. Например, за X можно обозначить рост индивидуума (см), X₁ обозначит рост 1-го индивидуума, а X_i — рост i-го индивидуума. Формула для определения среднего арифметического наблюдений (произносится «икс с чертой»):

= (Х₁ + Х₂ + … + X_n) / n

Можно сократить это выражение:

где (греческая буква «сигма») означает «суммирование», а индексы внизу и вверху этой буквы означают, что суммирование производится от i = 1 до i = n. Это выражение часто сокращают еще больше:

или

Медиана

Если упорядочить данные по величине, начиная с самой маленькой величины и заканчивая самой большой, то медиана также будет характеристикой усреднения в упорядоченном наборе данных.

Медиана делит ряд упорядоченных значений пополам с равным числом этих значений как выше, так и ниже ее (левее и правее медианы на числовой оси).

Вычислить медиану легко, если число наблюдений n нечетное. Это будет наблюдение номер (n + 1)/2 в нашем упорядоченном наборе данных.

Например, если n = 11, то медиана — это (11 + 1)/2, т. е. 6-е наблюдение в упорядоченном наборе данных.

Если n четное, то, строго говоря, медианы нет. Однако обычно мы вычисляем ее как среднее арифметическое двух соседних средних наблюдений в упорядоченном наборе данных (т. е. наблюдений номер (n/2) и (n/2 + 1)).

Так, например, если n = 20, то медиана — это среднее арифметическое наблюдений номер 20/2 = 10 и (20/2 + 1) = 11 в упорядоченном наборе данных.

Мода

Мода — это значение, которое встречается наиболее часто в наборе данных; если данные непрерывные, то мы обычно группируем их и вычисляем модальную группу.

Некоторые наборы данных не имеют моды, потому что каждое значение встречается только 1 раз. Иногда бывает более одной моды; это происходит тогда, когда 2 значения или больше встречаются одинаковое число раз и встречаемость каждого из этих значений больше, чем любого другого значения.

Как обобщающую характеристику моду используют редко.

Среднее геометрическое

При несимметричном распределении данных сред­нее арифметическое не будет обобщающим показа­телем распределения.

Если данные скошены вправо, то можно создать более симметричное распределе­ние, если взять логарифм (по основанию 10 или по основанию е) каждого значения переменной в наборе данных. Среднее арифметическое значений этих логарифмов — характеристика распределения для преобразованных данных.

Чтобы получить ме­ру с теми же единицами измерения, что и первона­чальные наблюдения, нужно осуществить обратное преобразование — потенцирование (т. е. взять анти­логарифм) средней логарифмированных данных; мы называем такую величину среднее геометрическое.

Если распределение данных логарифма приблизитель­но симметричное, то среднее геометрическое подобно медиане и меньше, чем среднее необработанных дан­ных.

Взвешенное среднее

Взвешенное среднее используют тогда, когда не­которые значения интересующей нас переменной x более важны, чем другие. Мы присоединяем вес w_i к каждому из значений x_i в нашей выборке для то­го, чтобы учесть эту важность.

Если значения x₁, x₂ … x_n имеют соответствующий вес w₁, w₂ … w_n, то взвешенное арифметическое среднее выглядит следующим образом:

Например, предположим, что мы заинтересованы в определении средней продолжительности госпита­лизации в каком-либо районе и знаем средний реа­билитационный период больных в каждой больнице. Учитываем количество информации, в первом при­ближении принимая за вес каждого наблюдения число больных в больнице.

Взвешенное среднее и среднее арифметическое идентичны, если каждый вес равен единице.

Размах (интервал изменения)

Размах — это разность между максимальным и минимальным значениями переменной в наборе данных; этими двумя величинами обозначают их разность. Обратите внимание, что размах вводит в заблуждение, если одно из значений есть выброс (см. раздел 3).

Размах, полученный из процентилей

Что такое процентили

Предположим, что мы расположим наши данные упорядоченно от самой маленькой величины перемен­ной X и до самой большой величины. Величина X, до которой расположен 1% наблюдений (и выше которой расположены 99% наблюдений), называется первым процентилем.

Величина X, до которой находится 2% наблюдений, называется 2-м процентилем, и т. д.

Величины X, которые делят упорядоченный набор значений на 10 равных групп, т. е. 10-й, 20-й, 30-й,…, 90 и процентили, называются децилями. Величины X, которые делят упорядоченный набор значений на 4 равные группы, т.е. 25-й, 50-й и 75-й процентили, называются квартилями. 50-й процентиль — это ме­диана.

Применение процентилей

Мы можем добиться такой формы описания рас­сеяния, на которую не повлияет выброс (аномальное значение), исключая экстремальные величины и определяя размах остающихся наблюдений.

Межквартильный размах — это разница между 1-м и 3-м квартилями, т.е. между 25-м и 75-м процентилями. В него входят центральные 50% наблюдений в упорядоченном наборе, где 25% наблюдений находятся ниже центральной точки и 25% — выше.

Интердецильный размах содержит в себе центральные 80% наблюдений, т. е. те наблю­дения, которые располагаются между 10-м и 90-м процентилями.

Мы часто используем размах, который содержит 95% наблюдений, т.е. он исключает 2,5% наблюдений снизу и 2,5% сверху. Указание такого интервала актуально, например, для осуществления диагностики болезни. Такой интервал называется референтный интервал, референтный размах или нормальный размах.

Дисперсия

Один из способов измерения рассеяния данных за­ключается в том, чтобы определить степень отклоне­ния каждого наблюдения от средней арифметической. Очевидно, что чем больше отклонение, тем больше изменчивость, вариабельность наблюдений.

Однако мы не можем использовать среднее этих отклонений как меру рассеяния, потому что положительные от­клонения компенсируют отрицательные отклонения (их сумма равна нулю). Чтобы решить эту проблему, мы возводим в квадрат каждое отклонение и находим среднее возведенных в квадрат отклонений; эта величина называется вариацией, или дисперсией.

Возьмем n наблюдений x₁, x₂, х₃, …, x_n, среднее которых равняется .

Вычисляем дисперсию:

В случае, если мы имеем дело не с генеральной совокупностью, а с выборкой, то вычисляется выборочная дисперсия:

Теоретически можно показать, что полу­чится более точная дисперсия по выборке, если разделить не на n, а на (n-1).

Единицы измерения (размерность) вариации — это квадрат единиц измерения первоначальных на­блюдений.

Например, если измерения производятся в килограммах, то единица измерения вариации будет килограмм в квадрате.

Среднеквадратическое отклонение, стандартное отклонение выборки

Среднеквадратическое отклоне­ние — это положительный квадратный корень из дисперсии.

Стандартное отклонение выборки — корень из выборочной дисперсии:

Мы можем представить себе стандартное отклоне­ние как своего рода среднее отклонение наблюдений от среднего. Оно вычисляется в тех же единицах (размерностях), что и исходные данные.

Если разделить стандартное отклонение на сред­нее арифметическое и выразить результат в процен­тах, получится коэффициент вариации.

Он являет­ся мерой рассеяния, не зависит от единиц измерения (безразмерный), но имеет некоторые теоретические не­удобства и поэтому не очень одобряется статистиками.

Вариация в пределах субъектов и между субъектами

Если провести повторные измерения непрерывной переменной у исследуемого объекта, то можно увидеть ее изме­нения (внутрисубъектные изменения). Это можно объяснить тем, что объект не всегда может дать точные и те же самые ответы, и/или ошибкой, погрешностью измерения. Однако при измерениях у одного объекта вариация обычно меньше, чем вариация единичного измерения в группе (межсубъектные изменения).

Например, вместимость легкого 17-летнего мальчика составляет от 3,60 до 3,87 л, когда измерения повторяются не менее 10 раз; если провести однократное измерение у 10 мальчиков того же возраста, то объем будет между 2,98 и 4,33 л. Эти концепции важны в плане исследования.

Связанные определения:
Выборочное среднее, среднее значение выборки
Выброс
Дисперсия (рассеяние, разброс)
Дисперсия выборки (выборочная дисперсия)
Коэффициент вариации
Максимум
Математическое ожидание дискретной случайной величины
Математическое ожидание непрерывной случайной величины
Медиана
Меры дисперсии, меры разброса
Минимум
Мода
Описательные статистики
Описательный анализ
Параметры рассеяния
Параметры центральной тенденции
Среднее значение
Среднеквадратичное отклонение популяции
Стандартная ошибка среднего
Стандартное отклонение

В начало

Содержание портала

Вставка математических знаков

В Word можно вставлять математические символы в уравнения и текст.

На вкладке Вставка в группе Символы щелкните стрелку рядом с надписью Формула и выберите Вставить новую формулу.

В области Работа с формулами в группе Символы на вкладке Конструктор щелкните стрелку Еще.

Щелкните стрелку рядом с именем набора символов, а затем выберите набор символов, который вы хотите отобразить.

Щелкните нужный символ.

Доступные наборы символов

В группе Символы в Word доступны указанные ниже наборы математических символов. Щелкнув стрелку Еще, выберите меню в верхней части списка символов, чтобы просмотреть группы знаков.

Основные математические символы

Часто используемые математические символы, такие как > и

Верхнее подчеркивание в Ворде

Помимо использования разных видов форматирования текста таких как: изменение шрифта, применение полужирного или курсивного начертания, иногда необходимо сделать верхнее подчеркивание в Ворде. Расположить черту над буквой довольно просто, рассмотрим несколько способов решения данной задачи.

С помощью «Диакритических знаков»

Благодаря панели символов сделать черточку сверху можно следующим образом. Установите курсор мыши в нужном месте по тексту. Перейдите во вкладку «Вставка» далее найдите и нажмите в области «Символы» на кнопку «Формула» и выберите из выпадающего меню «Вставить новую формулу».

Откроется дополнительная вкладка «Работа с формулами» или «Конструктор». Из представленных вариантов в области «Структуры» выберите «Диакритические знаки» и кликните по окну с названием «Черта».

В добавленном окне напечатайте необходимое слово или букву.

В результате получится такой вид.

Подчеркивание сверху посредством фигуры

Используя фигуры в Ворде, можно подчеркнуть слово как сверху, так и снизу. Рассмотрим верхнее подчеркивание. Изначально необходимо напечатать нужный текст. Далее перейти во вкладку «Вставка» в области «Иллюстрации» выбрать кнопку «Фигуры». В новом окне кликнуть по фигуре «Линия».

Поставить крестик над словом в начале, нажать и протянуть линию до конца слова, двигая вверх или вниз выровнять линию и отпустить.

Можно изменить цвет верхнего подчеркивания, нужно нажать по линии и открыть вкладку «Формат». Нажав по кнопке «Контур фигуры» указать нужный цвет. Также можно изменить вид подчеркивания и толщину. Для этого перейдите в подпункт ниже «Толщина» или «Штрихи».

В соответствии с настройками палочку можно преобразовать в штрихпунктирную линию, либо изменить на стрелку, в нужном направлении.

Благодаря таким простым вариантам, поставить черту над буквой или цифрой не займёт много времени. Стоит лишь выбрать наиболее подходящий способ из вышепредставленных.

Как посчитать среднее значение в Ворде?

Как в Ворде найти среднее значение в одном или нескольких столбцах таблицы?

Понятно, что можно скопировать её в Эксель и посчитать среднее там.

Но можно ли сделать это непосредственно в документе Ворд?

Конечно можно, но пересчитываться автоматически не будет, что может стать источником ошибок.

Сначала надо нарисовать таблицу с числами, щелкнуть мышкой в ячейку где будет записано среднее значение и тогда в верхнем меню появится пункт Макет.

Надо выбрать МакетФормула

В открывшемся окне выбираем функцию высчитывания среднего значения AVERAGE и ставим аргумент ABOVE (ABOVE — считать ячейки выше той в которой записана формула)

Нажимаем ОК и получаем результат

Если нужно рассчитать среднее по диапазону, то пишем как в Экселе из расчета , что первая строка таблицы имеет номер 1, первый столбец таблицы обозначается A ,например B2:C4.

При изменении данных таблицы придется принудительно обновить поле

Для обновления всех полей в выделенной области надо нажать F9 (например выделить всю таблицу и нажать F9)

Чтобы исключить ошибки, желательно в параметрах Word установить в разделе Экран галочку Обновлять поля перед печатью

Случайные
события обозначаются латинскими буквами
А,
В,
С,
… . Достоверное
событие обозначим через Е,
невозможное
– символом
.
РавенствоА = В
означает, что появление одного из этих
событий влечет за собой появление
другого.

Произведение
событий
А
и В
есть событие С = АВ,
состоящее в наступлении обоих событий
А
и В.

Сумма
событий
А
и В
есть событие С = А+В,
состоящее в наступлении хотя бы одного
из событий А
и В.

Разность
событий
А
и В
есть событие С = А–В,
состоящее в том, что А
происходит, а В
не происходит.

Противоположное
событие обозначается той же буквой. но
с чертой сверху (событие А;
– противоположное). ЕслиА
происходит, то
– не происходит.

События
А
и В
несовместны,
если АВ = .

События
(m = 1,2,…,n)
образуют полную группу, если в результате
опыта обязательно должно произойти
хотя бы одно из них; при этом
.

Если
результат опыта можно представить в
виде полной группы событий, которые
попарно несовместны и равновозможны,
то вероятность события равна отношению
числа
благоприятствующих этому событию
исходов опыта к общему числувсех возможных исходов, т.е.;
подравновозможными
понимаются события, которые в силу тех
или других причин не имеют объективного
преимущества одно перед другим.

Пример
1.
Из 30 студентов 10 имеют спортивные
разряды, какова вероятность того, что
выбранные наудачу три студента –
разрядники?

Решение.
Событие
А
– 3 наудачу выбранных студента –
разрядники. Общее число выбора 3 студентов
из 30 представляет собой выборку без
повторения, в которой важен только
состав, т.е.
.
Аналогично число благоприятствующих
событиюА
исходов опыта
.
Итак,

.

Пример
2.
На склад поступило N
изделий, среди которых M
бракованных. Определить вероятность
того, что среди
наугад взятых со склада изделий окажетсябракованных.

Решение.
Выбрать
изделий изN
можно
способами. Число способов выборабракованных изM
равно
,
причем каждый из них может быть дополнен
(n–m)
изделий из общего числа стандартных
изделий (N–M)
числом способов
.
Таким образом,

.

§3. Теоремы сложения и умножения вероятностей. Условная вероятность

Вероятность
суммы двух событий определяется по
формуле

.

Для
несовместных событий вероятность суммы
событий равна сумме вероятностей событий

.

Условной
вероятностью
событияА
называется вероятность появления этого
события, вычисленная в предположении,
что событие В
уже произошло. События А
и В
независимы,
если
.

Вероятность
произведения двух событий определяется
по формуле

.

Пример
1.
Два стрелка, для которых вероятности
попадания в мишень равны соответственно
0,7 и 0,8, производят по одному выстрелу.
Определить вероятность хотя бы одного
попадания в мишень.

Решение.
Пусть
событие А
–
попал первый стрелок. Событие В
– попал второй стрелок, тогда

Пример
2.
Вероятность поражения мишени для стрелка
равна
.
Если при первом выстреле зафиксировано
попадание, то стрелок получает право
выстрела по второй мишени. Вероятность
поражения обеих мишеней при двух
выстрелах равна 0,5. Определить вероятность
поражения второй мишени.

Решение.
Пусть
А
–
поражение первой мишени, В
–
поражение второй мишени, тогда

Пример
3.
Вероятность, что студент сдаст первый
экзамен, равна 0,9; второй – 0,9; третий –
0,8. Найти вероятность, что студентом
будет сдан: а) только первый экзамен; б)
только один экзамен; в) три экзамена; г)
по крайней мере два экзамена; д) хотя бы
один экзамен.

Решение.
Пусть
– студент сдастi-ый
экзамен
.

а) В
– студент сдаст только первый экзамен,
тогда

б) С
–
студент сдаст только один экзамен

в)
Событие D
–
студент сдаст все три экзамена

.

г)
Событие Е
–
студент сдаст по крайней мере два
экзамена

.

д)
Событие F
–
студент сдаст хотя бы один экзамен

Соседние файлы в папке ПРАКТИЧЕСКИЕ ЗАДАНИЯ

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

понедельник, 21 мая 2012

X с чертой наверху символ

Помимо использования разных видов форматирования текста таких как: изменение шрифта, применение полужирного или курсивного начертания, иногда необходимо сделать верхнее подчеркивание в Ворде. Расположить черту над буквой довольно просто, рассмотрим несколько способов решения данной задачи.

С помощью «Диакритических знаков»

Благодаря панели символов сделать черточку сверху можно следующим образом. Установите курсор мыши в нужном месте по тексту. Перейдите во вкладку «Вставка» далее найдите и нажмите в области «Символы» на кнопку «Формула» и выберите из выпадающего меню «Вставить новую формулу».

Откроется дополнительная вкладка «Работа с формулами» или «Конструктор». Из представленных вариантов в области «Структуры» выберите «Диакритические знаки» и кликните по окну с названием «Черта».

В добавленном окне напечатайте необходимое слово или букву.

В результате получится такой вид.

Подчеркивание сверху посредством фигуры

Используя фигуры в Ворде, можно подчеркнуть слово как сверху, так и снизу. Рассмотрим верхнее подчеркивание. Изначально необходимо напечатать нужный текст. Далее перейти во вкладку «Вставка» в области «Иллюстрации» выбрать кнопку «Фигуры». В новом окне кликнуть по фигуре «Линия».

Поставить крестик над словом в начале, нажать и протянуть линию до конца слова, двигая вверх или вниз выровнять линию и отпустить.

Можно изменить цвет верхнего подчеркивания, нужно нажать по линии и открыть вкладку «Формат». Нажав по кнопке «Контур фигуры» указать нужный цвет. Также можно изменить вид подчеркивания и толщину. Для этого перейдите в подпункт ниже «Толщина» или «Штрихи».

В соответствии с настройками палочку можно преобразовать в штрихпунктирную линию, либо изменить на стрелку, в нужном направлении.

Благодаря таким простым вариантам, поставить черту над буквой или цифрой не займёт много времени. Стоит лишь выбрать наиболее подходящий способ из вышепредставленных.

Сре́днее арифмети́ческое (в математике и статистике) множества чисел — число, равное сумме всех чисел множества, делённой на их количество. Является одной из наиболее распространённых мер центральной тенденции.

Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).

При стремлении количества элементов множества чисел стационарного случайного процесса к бесконечности среднее арифметическое стремится к математическому ожиданию случайной величины.

Содержание

Введение [ править | править код ]

Обозначим множество чисел X = (x₁, x₂, …, x_n), тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной ( x ¯ >> , произносится «x с чертой»).

Для обозначения среднего арифметического всей совокупности чисел обычно используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки x_i из этой совокупности μ = E есть математическое ожидание этой выборки.

На практике разница между μ и x ¯ >> в том, что μ является типичной переменной, потому что видеть можно скорее выборку, а не всю генеральную совокупность. Поэтому, если выборку представлять случайным образом (в терминах теории вероятностей), тогда x ¯ >> (но не μ) можно трактовать как случайную переменную, имеющую распределение вероятностей на выборке (вероятностное распределение среднего).

Обе эти величины вычисляются одним и тем же способом:

x ¯ = 1 n ∑ i = 1 n x i = 1 n ( x 1 + ⋯ + x n ) . >= >sum _^ x_= >(x_ +cdots +x_ ).>

Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.

В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.

Примеры [ править | править код ]

• Для получения среднего арифметического трёх чисел необходимо сложить их и разделить на 3:

x 1 + x 2 + x 3 3 . +x_ +x_ > >.>

• Для получения среднего арифметического четырёх чисел необходимо сложить их и разделить на 4:

x 1 + x 2 + x 3 + x 4 4 . +x_ +x_ +x_ > >.>

Непрерывная случайная величина [ править | править код ]

Если существует интеграл от некоторой функции f ( x ) одной переменной, то среднее арифметическое этой функции на отрезке [ a ; b ] определяется через определённый интеграл:

f ( x ) ¯ [ a ; b ] = 1 b − a ∫ a b f ( x ) d x . _ = >int _^f(x)dx.>

Здесь подразумевается, что a.>»> b > a . a.> a.>»/>

Некоторые проблемы применения среднего [ править | править код ]

Отсутствие робастности [ править | править код ]

Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, что означает, что среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.

Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако, этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее, если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.

Сложный процент [ править | править код ]

Если числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.

Например, если акции в первый год упали на 10 %, а во второй год выросли на 30 %, тогда некорректно вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 30 %) / 2 = 10 %; правильное среднее значение в этом случае дают совокупные ежегодные темпы роста, по которым годовой рост получается только около 8,16653826392 % ≈ 8,2 %.

Причина этого в том, что проценты имеют каждый раз новую стартовую точку: 30 % — это 30 % от меньшего, чем цена в начале первого года, числа: если акции в начале стоили $30 и упали на 10 %, они в начале второго года стоят $27. Если акции выросли на 30 %, они в конце второго года стоят $35.1. Арифметическое среднее этого роста 10 %, но поскольку акции выросли за 2 года всего на $5.1, средний рост в 8,2 % даёт конечный результат $35.1:

[$30 (1 — 0.1) (1 + 0.3) = $30 (1 + 0.082) (1 + 0.082) = $35.1]. Если же использовать таким же образом среднее арифметическое значение 10 %, мы не получим фактическое значение: [$30 (1 + 0.1) (1 + 0.1) = $36.3].

Сложный процент в конце 2 года: 90 % * 130 % = 117 % , то есть общий прирост 17 %, а среднегодовой сложный процент 117 % ≈ 108.2 % >approx 108.2%> , то есть среднегодовой прирост 8,2 %.

Направления [ править | править код ]

При расчёте среднего арифметического значений некоторой переменной, изменяющейся циклически (например, фаза или угол), следует проявлять особую осторожность. Например, среднее чисел 1° и 359° будет равно 1 ∘ + 359 ∘ 2 = +359^ > >=> 180°. Это число неверно по двум причинам.

• Во-первых, угловые меры определены только для диапазона от 0° до 360° (или от 0 до 2π при измерении в радианах). Таким образом, ту же пару чисел можно было бы записать как (1° и −1°) или как (1° и 719°). Средние значения каждой из пар будут отличаться: 1 ∘ + ( − 1 ∘ ) 2 = 0 ∘ +(-1^ )> >=0^ >, 1 ∘ + 719 ∘ 2 = 360 ∘ +719^ > >=360^ >.
• Во-вторых, в данном случае, значение 0° (эквивалентное 360°) будет геометрически лучшим средним значением, так как числа отклоняются от 0° меньше, чем от какого-либо другого значения (у значения 0° наименьшая дисперсия). Сравните:

• число 1° отклоняется от 0° всего на 1°;
• число 1° отклоняется от вычисленного среднего, равного 180°, на 179°.

Среднее значение для циклической переменной, рассчитанное по приведённой формуле, будет искусственно сдвинуто относительно настоящего среднего к середине числового диапазона. Из-за этого среднее рассчитывается другим способом, а именно, в качестве среднего значения выбирается число с наименьшей дисперсией (центральная точка). Также вместо вычитания используется модульное расстояние (то есть, расстояние по окружности). Например, модульное расстояние между 1° и 359° равно 2°, а не 358° (на окружности между 359° и 360°==0° — один градус, между 0° и 1° — тоже 1°, в сумме — 2°).

Здесь легко и интересно общаться. Присоединяйся!

в ворде набирай код – маркер перед знаком.
знак у, код 035F,Alt+X : результат ͟y снизу
k, 035E,Alt+X ; результат ͞k – сверху.
В символах есть коды. и волнистых, и прочих…: )

если в ворде то вставить символ или надстрочным шрифтом (в свойствах шривта поставить галочку надстрочныу и в нужном месте поставить черточку)

В ворде есть переход в формулы жми:
ВСТАВКА – ФОРМУЛЫ – ДИАКРИТИЧЕСКИЕ ЗНАКИ и выбирай знак, в квадратике пиши переменную.
А так есть мастера формул. Международный – это MathType. В нём можно сделать всё, только язык надо зхнать : TeX

Вставка математических знаков

В Word можно вставлять математические символы в уравнения и текст.

На вкладке Вставка в группе Символы щелкните стрелку рядом с надписью Формула и выберите Вставить новую формулу.

В области Работа с формулами в группе Символы на вкладке Конструктор щелкните стрелку Еще.

Щелкните стрелку рядом с именем набора символов, а затем выберите набор символов, который вы хотите отобразить.

Щелкните нужный символ.

Доступные наборы символов

В группе Символы в Word доступны указанные ниже наборы математических символов. Щелкнув стрелку Еще, выберите меню в верхней части списка символов, чтобы просмотреть группы знаков.

Основные математические символы

Часто используемые математические символы, такие как > и

⃗ Надстрочный символ стрелка вправо

Вектор, векторное поле, верхний индекс

U+20D7

Нажмите, чтобы скопировать и вставить символ

Техническая информация

Название в Юникоде	Combining Right Arrow Above
Номер в Юникоде
Раздел	Комбинируемые диакритические знаки для символов
Версия Юникода:	1.1 (1993)

Значение символа

В геометрии, надстрочной стрелкой обозначается вектор — прямой отрезок имеющий начало и конец.

Символ «Надстрочный символ стрелка вправо» был утвержден как часть Юникода версии 1.1 в 1993 г.

Свойства

Версия	1.1
Блок	Комбинируемые диакритические знаки для символов
Тип парной зеркальной скобки (bidi)	Нет
Композиционное исключение	Нет
Изменение регистра	20D7
Простое изменение регистра	20D7

Похожие символы

Надстрочный символ По часовой стрелке

Надстрочный символ стрелка влево

Короткая стрелка, указывающая направо.

Длинная стрелка, указывающая налево.

Длинная стрелка, указывающая направо.

Стрелка вправо над стрелкой влево

Стрелка влево, упирающаяся в планку.

С-образная правая стрелка против.

Стрелка влево-вправо с чертой

Волнистая стрелка влево-вправо

Лево право белая стрелка

Стрелка влево-вправо с двойным.

Двойная стрелка влево-вправо

Кодировка

Кодировка	hex	dec (bytes)	dec	binary
UTF-8	E2 83 97	226 131 151	14844823	11100010 10000011 10010111
UTF-16BE	20 D7	32 215	8407	00100000 11010111
UTF-16LE	D7 20	215 32	55072	11010111 00100000
UTF-32BE	00 00 20 D7	0 0 32 215	8407	00000000 00000000 00100000 11010111
UTF-32LE	D7 20 00 00	215 32 0 0	3609198592	11010111 00100000 00000000 00000000

Наборы с этим символом:

© Таблица символов Юникода, 2012–2022.
Юникод® — это зарегистрированная торговая марка консорциума Юникод в США и других странах. Этот сайт никак не связан с консорциумом Юникод. Официальный сайт Юникода располагается по адресу www.unicode.org.

Мы используем 🍪cookie, чтобы сделать сайт максимально удобным для вас. Подробнее