Xmin xmax как найти

На экране современного компьютера
можно получить не только последовательности
букв, цифр и других символов, но и
разнообразные рисунки, схемы и т.д. Для
этого в языке Программирования включаются
специальные средства — графические
процедуры. Количество пикселей (светящихся
точек ) на экране зависит от типа
графического адаптера(видеокарты) и для распространенного
адаптера VGA составляет 1024×768.

Так
как же осуществляется построение
графиков функций?

Допустим требуется построить
график функции у=sin(x). Кроме кривой,
изображающей график этой функции, на
экране должны быть высвечены координатные
оси Ох и Оу.

В рассматриваемых задачах
необходимо нарисовать на экране график
заданной функции, например:y=Sin(x) , xI[xmin,
xmax].

Трудность заключается в том, что
значения xmin, xmax, уmin, уmax могут быть
отрицательными, дробными, очень большими
или очень маленькими, а точки экрана
нумеруются целыми положительными
числами по горизонтальной оси от 0 до
1279, по вертикальной оси от 0 до 967, и эта
ось направлена вниз.

Задача решается в два этапа:

1) выясняются пределы изменения
х и у заданной функции (для этого

надо провести анализ функции)

2) рисуется график функции с
пересчетом координат (х, у) каждой

точки графика в экранные координаты
(i, j).

Выбор пределов
изменения аргумента и заданной функции

Задаём интервал изменения х: от
хmin до хmax и распечатываем значения
функции с таким шагом h (по х), чтобы в
таблице было 10 – 20 строчек, например,
так:

program grafic1;

var

a, x, y, xmin, xmax, h: real;

begin

write(‘Введите параметр а=’);
readln(а);

write(‘Введите х min и max’);

readln( xmin, xmax);

h:=(xmax — xmin)/20;

x:=xmin;

while x<=xmax do

begin

y:=a*sin(x);

writeln(x:7:1, y:7:1);

x:=x+h;

end;

end.

    Из таблицы на экране можно
примерно определить максимальное и
минимальное значения функции в этом
интервале ymax и ymin. Если функция в задаче
задана параметрически, т.е. x(t) и y(t), где
t- параметр, то в программе именно его
следует изменять с равным шагом, а
вычисленные по формулам значения x и y
–выводить на экран. Если изображаемая
функция определена на промежутке
-∞<t<+∞, то для построения графика
необходимо взять достаточно большие,
но конечные значения параметра, например,
-10<t<10. С другой стороны, изображаемые
функции всегда состоят из комбинации
элементарных функций, свойства которых
известны. Поэтому можно определить
пределы изменения значения функции,
анализируя ее вид. Например, для данной
функции y(x)=sin(x) легко видеть, что sin(x)
изменяется от –1 до 1.

Программа рисования
графика функции

Алгоритм рисования графика
функции:

1. Задание max и min значений аргумента
и функции, параметров

функции, вычисление коэффициентов
пересчета;

2. Подпись графика;

3. Рисование осей;

4. В цикле:

a. вычисление очередных значений
аргумента и функции

b. изображение на экране точки
(x, у);

Оси координат необходимо
изобразить на графике с помощью операторов
Line. При этом нужно помнить, что это прямые
у=0 (ось абсцисс) и х=0 (ось ординат).

Процедура CloseGraph
завершает работу в графическом режиме
и переводит компьютер в текстовый режим.

В программе, приведенной ниже,
строится график функции y=Sin(x).

program sin_x;

uses crt,graph;

var x, y, x0, y0, k, vga,vgahi:integer;

begin

initgraph(vga,vgahi,’c:prgbpbgi’);

line(20,240,620,240);

line(320,20,320,400);

X0:=320;

Y0:=240;

k:=50;

for X:=-320 to 320 do

begin

y:=trunc(k*sin(x/k));

PutPixel(x0+x,y0-y,4);

end;

OutTextXY (50,440,’Grafic y=sin x’);

readln;

closegraph;

end.

Применение
производной.

Нахождение экстремумов (
максимумов и минимумов) функции.

Краткая теория. (Разобрать, записать в тетрадь основные понятия, ответить на
вопросы по теоретической части) .

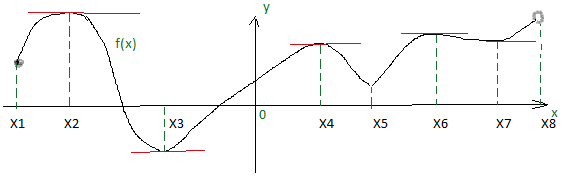
 Рисунок 1.  Рассмотрим внутренние точки области определения функции,
изображенной на рис.1, в которых производная равна нулю или не существует. В точках,
где производная равна 0, касательная параллельна оси ОХ. Это точки Х₂,
Х₃, Х₄, Х₆ и Х₇.  В точке Х₅
касательную провести нельзя, т.к. острый график, поэтому в этой точке
производная не существует.  На концах промежутка в точках Х₁ и Х₈
тоже касательные провести нельзя, так как нужна окрестность точки. На концах
промежутка экстремумов не бывает.

Определение.  Точки,
в которых производная функции равна 0 или не существует называются критическими.

На
нашем  рисунке это точки Х₂, Х₃,
Х₄, Х_5, Х₆ и Х₇.  Среди этих точек
могут быть точки максимума ( max ) и  минимума ( min ), которые называются точками экстремума       ( X_max и X_min ).  Значения функции в
этих точках называют экстремумами функции   и обозначают f_max (X_max)  и  f_min (X_min). 

Необходимым условием существования экстремумов является
равенство нулю производной или если производная не существует, то есть необходимое
условие – это наличие критических точек. (Это теорема Ферма), но этого условия
еще не достаточно. Чтобы функция имела экстремум в некоторой точке, надо, чтобы
при переходе через эту точку производная меняла свой знак, то есть надо, чтобы
возрастание менялось на убывание, или убывание на возрастание. Если такой смены
нет, то в этой критической точке не будет экстремума.

Если
знак производной меняется с  (+ ) на (- ) – это точка max, если знак производной меняется с  (- )
на (+ ) – это точка min.

На
рис.1:  Точка Х₂ является точкой max, т.к. при переходе через
эту точку возрастание сменилось убыванием ( f ´(x) поменяла знак с  (+ ) на (- )). Такими же будут
точки  Х₄   и Х_6.             В
точках Х₃   и  Х₅   при переходе  f ´(x) поменяла знак с  (- ) на (+ ). Это точки min.

В  критической точке Х₇  не произошло
смены знака производной (функция возрастала до этой точке и возрастает после
этой точки). Здесь никакого экстремума нет. Это  точка перегиба. Не будет существовать экстремумов и в точках, в которых график функции
будут разрываться. На нашем рисунке такого случая нет.

Вывод. Для существования
экстремумов необходимо выполнение двух условий:

1.       Существование критических точек.

2.       Смена знака производной при переходе через критическую точку.

Ответить на
вопросы.

Нахождение экстремумов
функции осуществляют по следующему плану:

1.      Найти
область определения функции.

2.      Найти
производную.

3.      Найти
критические точки ( приравнять производную к нулю).

4.      На
числовой прямой отметить найденные критические точки, выделить           
полученные числовые промежутки и проверить знак производной в каждом из них.

5.      Записать,
где получились точки максимума или минимума, (а может быть и перегиба, если
знак производной не менялся при переходе через точку, или разрыва).

6.      Вычислить
значение  экстремумов функции (значение самой функции в точках экстремума.

7.      Для
наглядности или когда надо построить график заданной функции, заносятся все
полученные данные в таблицу.

Рассмотрим примеры.

Пример 1. Найти
критические точки функции f(x)
=x³
-7x²
-5x +6 (в
ответ записать большее значение).          Решение.

(В данном примере надо выполнить
только три первых пункта плана.)

1.      D(
f ) = (- ∞; + ∞).

2.      Найдем
производную f ´(x)
=(x³ -7x²
-5x +6)´ =3х² – 14х -5

3.      3х²
– 14х -5= 0      D= (-14)² — 4·3·(-5) = 196
+ 60 = 256 = 16²

X₁
= (14+16)/(2·3) = 5      X₂
= (14 — 16)/(2·3) = — 1/3     Ответ: 5

Пример 2. Исследовать
функцию f(x)
=2x³  —
24x на
экстремумы ( сделать таблицу, в ответ записать а) точку минимума; б) максимум
функции).  

 Решение.

(В этом задании надо
выполнить все пункты плана.)

1.      D(
f ) = (- ∞; + ∞).

2.      Найдем
производную f ´(x)
=(2x³ — 24x)´=
6х² – 24

3.      
6х²
– 24=0 Здесь неполное
квадратное уравнение, вынесем за скобки общий множитель  6 (х²
– 4)=0;    х² – 4=0;     х² = 4;     х₁ =2 и х₂=
— 2  это критические
точки.   

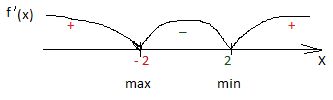
4.      
 Знаки в
промежутках определяют,  выбирая любые числа из каждого промежутка и подставляя
в производную. Например, из промежутка ( -∞; -2)
можно взять число         х= — 3.        6· (-3)² -24 = 6· 9 -24=30
> 0  (если квадратичная функция, знаки чередуются).       

5.      
     Xmax
= -2     Xmin = 2

   6. f_max
(-2)
=2·(-2)³  — 24·(-2)=32  

    
 f_min
(2)
=2·(2)³  — 24·(2)= — 32

7.

X	( -∞; -2)	-2	(-2; 2)	2	(2 ; +∞)
f ´ (x)	+	0	—	0	+
f (x)	↑	32	↓	-32	↑
	max		min

Ответ:  
а)  2               б)  32.

Пример 3. Исследовать
функцию f(x)
= Х +(1/х) на экстремумы ( сделать таблицу, в ответ
записать  а) критические точки; б)  точку максимума; в) минимум функции).

Решение.

(В этом задании надо
выполнить все пункты плана.)

1.     
D( f
) = (- ∞; 0)  U (0; + ∞).      ( так
как  в выражении 1/х   х≠0)

2.     
Найдем
производную f ´(x)
=( Х +(1/х))´= 1 — (1 / х²) = (х² -1) / х²   

3.       (х²
-1) = 0     х² =1      x₁
= -1   x₂
=1  при х=0 производная не существует.  
Критических точек 3.
Это  -1;
0; 1.                               

4.          

Здесь функция не квадратичная
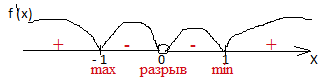
функция и знаки надо проверять в каждом  промежутке.  Например, из промежутке  
( -1; 0) можно взять х= — 0,5.    1 — (1 / х²) =
1 – (1 /( — 0,5)²) = 1 –( 1/0,25)= 
1 – 16 =-15 <0 ( поставили на рисунке знак минус.). Так проверяем знак в
каждом промежутке в этом задании.

5. В этом примере две
точки экстремума   Xmax = -1     Xmin
= 1

6.
f_max
(-1)
=  -1
+(1/-1)= -2

    
 f_min
(1)
= 1 +(1/1) = 2

7.

X	( -∞; -1)	-1	(-1; 0)	0	(0 ; 1)	1	(1 ; +∞)
f ´ (x)	+	0	—	Не существует	—	0	+
f (x)	↑	— 2	↓		↓	2	↑
	max		разрыв		min

Ответ:  а)  -1;  0;  1.          б)  —
1.         в)  2.

Решить самостоятельно.

1.     Найти
критические точки функции f(x)
= -2x³
+6x²
+ 48x — 16 (в
ответ записать меньшее значение).  

2.     Исследовать
функцию f(x)
=x³
— 27x + 20 на
экстремумы ( без таблицы, в ответ записать а) точку минимума; б) минимум
функции).  

3.      Исследовать
функцию f(x)
=3x⁴ —
4x³
+ 5 на
экстремумы ( сделать таблицу, в ответ записать  а) наименьшую критическую
точку; б) точку экстремума; в) экстремум функции; г) что происходит с функцией
в критической точке х=0 ?).  

Ответы на вопросы.

1.    Производная
равна нулю или не существует.

2.    Точки
минимума и максимума.

3.    Значение
функции в точках экстремума.

4.    Максимум
функции и минимум функции.

5.    Существование
критических точек.

6.    Смена
знака производной в этой точке.

7.    Максимум,
если знак меняется с ( + ) на ( — ).

8.    Минимум,
если знак меняется с ( — ) на ( + ).

Ответы на задачи.

1.    Критические
точки   х= -2 и х=4;      меньшее  -2

2.      а)
Точка минимума х=  3

б) 
минимум функции f(x)
=  -34

3.    а)
наименьшая критическая точка х = 0

б) 
точка экстремума    х=1

в) экстремум
функции    f(1) = -1

г)
что происходит с функцией в т. х=0?   Перегиб графика.

Здесь мы узнаем о стандартизации и нормализации, где, когда и почему использовать с реальными наборами данных.

Стандартизация-

В машинном обучении это метод, в котором значения центрируются вокруг среднего с единичным стандартным отклонением (µ = 0 и σ = 1). Это означает, что атрибуты среднего значения равны нулю, а результирующее распределение имеет стандартное отклонение единицы.

Формула стандартизации:

X’ = ( Xi — µ ) / σ

где σ — стандартное отклонение, µ — среднее, а Xi — значения входных характеристик.

Пример с набором данных из реального мира —

Здесь у нас есть простой набор данных, мы берем только целые значения и применяем train_test_split

sklearn.preprocessing.StandardScaler использует библиотеку из sklearn для стандартизации.

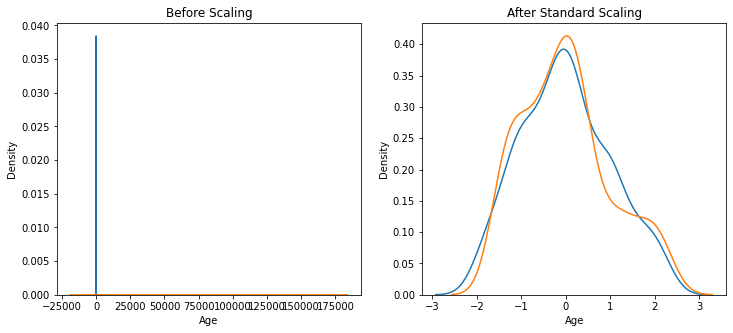
После применения набора данных Standard Scaler, похожего на приведенный ниже

На приведенном выше рисунке показано среднее значение, равное 0, а стандартное отклонение — 1, что удовлетворяет нашей теории стандартизации.

Эффект стандартизации —

Здесь, как вы можете видеть, есть диаграмма разброса до масштабирования и после масштабирования, и вы видите, что после стандартизации нет никакого эффекта.

После стандартизации график функции плотности вероятности выглядит так, как показано ниже.

Почему важна стандартизация?

В машинном обучении наша цель — улучшить модели и показатели точности. Таким образом, для улучшения результатов и хорошей модели прогнозирования используется стандартизация.

На приведенном выше рисунке, как вы можете видеть, есть два показателя precision_score, которые определены без стандартизации и со стандартизацией соответственно, и есть значительные улучшения в оценке точности, что является нашей задачей.

Нормализация —

Нормализация — это метод, который часто применяется как часть подготовки данных для машинного обучения. Цель нормализации — изменить значения числовых столбцов в наборе данных для использования общей шкалы без искажения различий в диапазонах значений или потери информации. Нормализация — это метод масштабирования, при котором значения смещаются и масштабируются таким образом, чтобы в конечном итоге они оказались в диапазоне от 0 до 1. Это также известно как масштабирование минимум-максимум.

Формула нормализации:

X ’= (X — Xmin) / (Xmax — Xmin)

Здесь Xmax и Xmin — максимальное и минимальное значения признака соответственно.

• Когда значение X является минимальным значением в столбце, числитель будет 0, и, следовательно, X ’равно 0.
• С другой стороны, когда значение X является максимальным значением в столбце, числитель равен знаменателю, и, таким образом, значение X ’равно 1.
• Если значение X находится между минимальным и максимальным значением, тогда значение X ’находится между 0 и 1.

Пример с набором данных из реального мира —

Здесь у нас есть простой набор данных, и мы берем только целые значения.

Примените библиотеку train_test_split и MinMaxScaler из sklearn.

после записи вывод похож на приведенный ниже.

Эффект нормализации —

Взгляните на график и посмотрите, есть ли какие-либо изменения до и после нормализации.

Здесь, как вы можете видеть, есть диаграмма рассеяния до масштабирования и после масштабирования, и вы видите, что после нормализации нет никакого эффекта.

После стандартизации график функции плотности вероятности похож на приведенный ниже.

Стандартизация против нормализации —

• Нормализацию удобно использовать, когда вы знаете, что распределение ваших данных не соответствует распределению Гаусса. Это может быть полезно в алгоритмах, которые не предполагают какое-либо распределение данных, таких как K-Nearest Neighbours и Neural Networks.
• С другой стороны, стандартизация может быть полезна в случаях, когда данные соответствуют гауссовскому распределению. Однако это не обязательно должно быть правдой. Кроме того, в отличие от нормализации, стандартизация не имеет ограничивающего диапазона. Таким образом, даже если в ваших данных есть выбросы, на них не повлияет стандартизация.

Вывод —

В конце концов, выбор использования нормализации или стандартизации будет зависеть от вашей проблемы и алгоритма машинного обучения, который вы используете. Не существует жесткого правила, которое подскажет, когда нормализовать или стандартизировать данные. Вы всегда можете начать с подгонки модели к необработанным, нормализованным и стандартизованным данным и сравнить производительность для достижения наилучших результатов.

Рекомендуется подогнать масштабатор к обучающим данным, а затем использовать его для преобразования данных тестирования. Это позволит избежать утечки данных в процессе тестирования модели. Кроме того, обычно не требуется масштабирование целевых значений.

Обучение и ресурсы:

[1] Для кода и концепции: https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html

[1] Для кода и концепции: https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html

[3] Код и концепция: https://www.analyticsvidhya.com/blog/

В результате
статистического наблюдения мы получаем
неупорядоченный ряд отдельных значений,
работать с которым затруднительно.

Во-первых, результаты
наблюдений необходимо упорядочить, или
проранжировать, то есть расположить
все значения в порядке возрастания или
убывания.

Ряд, где значения
признака располагаются в порядке
возрастания или убывания, называется
ранжированным(упорядоченным)рядом распределения.

Теперь можно
определить величину интервала.

Правильное
установление величины интервала имеет
первостепенное значение для образования
качественно однородных групп. Например,
показатель: «темпы роста» — 93%, 98%,
101%. Нецелесообразно делать интервал
95%-105%, то есть объединять увеличивших и
снизивших производство в одну группу.
Необходимо сделать интервалы 95%-100%,
100%-105%.

Если совокупность
однородна по своему составу, то в основу
построения интервального ряда следует
положить принцип равенства интервалов.

Однородная
совокупность— такая совокупность,
когда самые существенные признаки для
каждой ее единицы являются в основном
одинаковыми.

Величина интервала
определяется по формуле:

Xmax
— Xmin R

i
= ——————- = ———— ,

n
n (3.3.1)

где i
— величина интервала,

Xmax
— максимальное значение признака
в ряду распределения;

Xmin
— минимальное значение признака
в ряду распределения;

R
—— размах вариации (разница междуXmaxиXmin);

n
— число групп.

Возникает вопрос
о числе групп, которое зависит от
изменчивости признака и числа наблюдений.
Здесь нет строго научных приемов, всякий
раз эта задача решается с учетом
конкретных обстоятельств.

Чем интенсивнее
меняется признак и чем больше единиц
совокупности, тем больше образуется
групп.

При равенстве
интервалов для ориентировки существует
формула, предложенная американским
ученым Стерджессом:

n
= 1 + 3,322 lg
N.
(3.3.2)

При 200 единицах (N= 200)n= 1 + 3,322 *lg200 = 9.

В экономической
практике в большинстве своем применяются
неравные интервалы, прогрессивно
возрастающие или убывающие.

Арифметическая и
геометрическая прогрессия:

h
_i+1
= h _i
+ a(«+»
возрастающая, «-» убывающая);

h
_i+1
= h _i
* q(«>1»
возрастающая, «<1» убывающая).

Такая необходимость
возникает, когда колеблемость признака
осуществляется неравномерно и в больших
пределах. Например, группировка торговых
предприятий по объему товарооборота.
Разница в товарообороте для мелких
магазинов, ларьков, палаток в несколько
миллионов рублей имеет решающее значение,
а для крупных (например, универсам) –
несущественное.

При определении
величины интервала важное значение
имеет точное установление границ,
которые обозначаются указанием значений
«от» и «до». Например, «от 1
до 3» : 1 — 3, 4 — 7, 8 — 10 (дискретные значения).

Однако на практике
нередко (для варьирующих признаков)
одно и то же число служит верхней и
нижней границами двух смежных групп :
до 90, 90-100, 100-110, 110-120. Здесь вопрос решается
двояко: по принципу «включительно»
и «исключительно». «Включительно»
90 должно войти в первую группу, а
«исключительно» 90 — во вторую
группу. В этом случае лучше делать
открытый интервальный ряд и по последнему
интервалу определять принцип. Например,
«свыше 150» (150 входит в предыдущую
группу, то есть принцип «включительно»)
и «150 и более» (150 входит в эту группу,
то есть действует принцип «исключительно»).

Открытый интервал:
«до 90». Закрытый интервал: «90-100».

Середина интервала
определяется как полусумма верхней и
нижней границ интервала:

Интервал	Решение	Середина интервала
до 90	(70 + 90) : 2	80
90-110	(90 + 110) : 2	100
110-150	(110 + 150) : 2	130
150-200	(150 + 200) : 2	175
свыше 200	(200 + 250) : 2	225

Если величина
интервала, рассчитанная по формуле

Xmax
— Xmin

i
= ——————- , имеет один знак
до запятой (например:i=0,88,i= 1,585,

n

i=
4,8), то значения округляются до десятых:
0,9; 1,6; 4,8.

Если два знака до
запятой (15,985), то округляется до целых
(16). Если 3-, 4- значные значения, то
округляют до ближайшего числа, кратного
100 или 50. Например, 557 550.

При статистическом
исследовании иногда приходится
производить вторичную группировку.
Основными методами вторичной группировки
являются:

• метод
  изменения интервала;

• долевая
  перегруппировка.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #