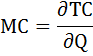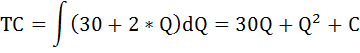Задача как найти максимальную прибыль

Даны функция спроса на продукцию монополиста

Q = 26 — 0,5 × P

и функция общих затрат

ТС = 120 — 8 × Q + Q².

Найти максимальную прибыль и соответствующую цену.

Решение:

Запишем обратную функцию спроса:

P = 52 — 2 × Q.

Общий доход найдём по формуле:

TR = Р × Q = (52 — 2 × Q) × Q = 52 × Q — 2 × Q².

Найдём предельный доход как производную от функции общего дохода:

MR = TR’ = (52 × Q — 2 × Q²)’ = 52 — 4 × Q.

Определим функцию предельных затрат, взяв производную от функции общих затрат:

MC = TC’ = (120 — 8 × Q + Q²)’ = — 8 + 2 × Q.

Условие максимизации прибыли на рынке несовершенной конкуренции имеет вид:

MC = MR

— 8 + 2 × Q = 52 — 4 × Q

Q = 10 — оптимальный объём производства, при котором прибыль максимальна.

Цена на продукцию монополии будет соответственно равна

P = 52 — 2 × 10 = 32.

Прибыль вычислим по формуле:

П = TR — TC = P × Q — 120 + 8 × Q — Q² = 32 × 10 — 120 + 8 × 10 — 10² = 180.

Задача
максимизации прибыли фирмы имеет вид

х₁,х₂– переменные,

.

Условия
первого порядка для нее таковы:

Это
те же самые условия, что и условия
равенства стоимости предельного
продукта фактора цене этого фактора,
приведенные в тексте. Посмотрим, как
выглядит поведение фирмы, максимизирующее
прибыль, в случае производственной
функции Кобба-Дугласа.

Предположим,
что функция Кобба-Дугласа задана в виде
.
Тогда указанные два условия первого
порядка принимают вид:

Решая
систему, получаем

,

,

это
выражения для спроса на два фактора
производства как функции выбора
оптимального выпуска.

Далее
надо найти выражение для оптимального
выбора объема выпуска. Подставляя
выражения для оптимального спроса на
факторы в производственную функцию
Кобба-Дугласа, получаем выражение

.

Вынеся
уза скобки в левой части уравнения,
получаем

,

или

.

Это
выражение для функции предложения
фирмы с производственной функцией
Кобба-Дугласа.

Наряду
с выведенными выше функциями спроса
на факторы
ионо дает нам полное решение задачи
максимизации прибыли.

4. Модель Леонтьева многоотраслевой экономики

4.1. Балансовые соотношения

Модель
Леонтьева — это статическая модель
линейной многоотраслевой экономики.
В её основе лежат следующие предположения.

1.
В экономической системе производятся,
продаются, покупаются, потребляются и
инвестируются п
продуктов.

2.
Каждая отрасль хозяйства является
«чистой», то есть производит только
один продукт. Разные отрасли производят
разные продукты.

3.
Под производственным процессом в каждой
отрасли понимается преобразование
типов ресурсов в определённый продукт.
При этом соотношение
затраченных продуктов предполагается
постоянным.
Это означает, что, если для производства
единицы j-го
продукта требуется затратить
единицi
–го ресурса,
то для выпуска 
единиц j-го
продукта следует затратить уже
единицi–го
ресурса. Значит, независимо от масштаба
производства, удельный выпуск и
соотношения затрат предполагаются
постоянными. Часть продукции идёт на
внутрипроизводственное потребление
данной отраслью (данным предприятием)
и другими отраслями, а другая часть
предназначена для целей конечного (вне
сферы материального производства)
личного и общественного потребления.

Обозначим:

—
общий валовый объём продукции i–й
отрасли,

—
объём продукции i–й
отрасли,
потребляемый j–й
отраслью в процессе производства при
выпуске объёма продукции

-объём
конечного продукта i–й
отрасли для непроизводственного
потребления,
.

Так
как валовый объём продукции любой i–й
отрасли равен суммарному объёму
продукции, потребляемой п
отраслями и конечного продукта, то

,.
(52)

Уравнения
(52) называются соотношениями баланса:

Так
как продукция разных отраслей имеет
разные измерения, то в дальнейшем будем
иметь в виду стоимостный баланс.

В
стоимостном межотраслевом балансе
все величины, входящие в (52), имеют
стоимостное выражение.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Задача №1. Расчёт экономической прибыли конкурентной фирмы

Фирма, находясь в условиях совершенной конкуренции, имеет следующую функцию общих затрат:

ТС = 140 + 10 × Q + 40 × Q².

При каком выпуске прибыль фирмы достигнет максимума, если цена установилась на уровне 250 ден. ед.? Определить размер прибыли фирмы.

Будут ли в длительном периоде в эту отрасль стремиться войти новые фирмы?

Решение:

Наличие  в составе общих затрат фиксированных (постоянных) затрат (FC = 140) свидетельствует о том, что речь идёт о краткосрочном периоде.

Найдём объём производства, при котором прибыль будет максимальна. Условие максимизации прибыли на рынке совершенной конкуренции в краткосрочном периоде имеет вид:

Р = МС = МR = AR.

Определим функцию предельных издержек фирмы: найдём производную общих издержек.

МС = (ТС)’ = 10 + 80 × Q.

Приравняем эту функцию к цене равной 250.

10 + 80 × Q = 250

80 × Q = 240

Q = 3

Вычислим прибыль фирмы при объёме выпуска равном 3 по формуле:

П = TR — TC = P × Q — TC = 250 × 3 — (140 + 10 × 3 + 40 × 3²) = 220 ден. ед.

В долгосрочном периоде наличие неотрицательной экономической прибыли будет привлекать в отрасль новые фирмы.

Задача № 2. Определение рыночной цены и отраслевого выпуска продукции

В отрасли действуют 130 одинаковых фирм. Издержки производства каждой фирмы описываются функциями

ТС =Q³ — 36*Q² + 384*Q,

где

Q — объём производства в тысячах штук. Найти рыночную цену и отраслевой выпуск продукции, при которых на конкурентном рынке устанавливается долгосрочное равновесие.

Решение:

В долгосрочном периоде на рынке совершенной конкуренции соблюдается равенство:

P = MC = MR = AR = minAC.

Найдём функцию средних издержек каждой фирмы по следующей формуле:

АС = ТС / Q = Q² — 36*Q + 384

Далее необходимо найти минимум данной функции. Для этого определим производную функции АС и приравняем её к нулю.

2*Q — 36 = 0

Q = 18

AC(18) = 18² — 36*18 + 384 = 60

Так как Р = minAC в долгосрочном периоде, следовательно, рыночная цена равна Р = 60.

Найдём отраслевой выпуск. Так как каждая из фирм отрасли производит 18 тысяч штук продукции, значит 130 фирм произведут:

Q_отр. = 18*130 = 2340 тысяч штук

Задача № 3. Определение рыночной цены в долгосрочном периоде

Конкурентная фирма находится в состоянии равновесия в долгосрочном периоде и имеет следующие затраты: TC = Q³ — 38*Q² + 418*Q. Определите цену на этом рынке в долгосрочном периоде.

Решение:

В долгосрочном периоде цена в условиях соверешенной конкуренции устанавливается на уровне минимума средних затрат. При этом фирма совершенный конкурент получает нулевую экономическую прибыль.

Условие равновесия на рынке будет иметь вид:

Р = МС = МR = AR = min AC

Найдём средние затраты фирмы по формуле:

АС = ТС / Q = Q² — 38*Q + 418

Определим минимум функции средних затрат. Для нахождения экстремума функции  приравняем к нулю её производную:

АС’ = 2*Q — 38

2*Q — 38 = 0

Q = 19

При выпуске Q = 19 средние затраты будут равны:

АС = 19² — 38*19 + 418 = 57.

Таким образом, цена в долгосрочном периоде будет равна 57.

Задача № 4. Расчёт рыночной цены, при которой фирма уйдёт с рынка

Общие затраты фирмы, действующей на рынке совершенной конкуренции, составляют

0,5*Q³ — 15*Q² + 300*Q + 250 000.

При какой цене фирме становится невыгодным работать на этом рынке в краткосрочном периоде?

Решение:

В краткосрочном периоде фирма совершенный конкурент уйдёт с рынка, если цена окажется меньше  минимума её средних переменных издержек: Р < min AVC.

Найдём переменные издержки фирмы, а точнее запишем функцию переменных издержек:

VC = 0,5*Q³ — 15*Q² + 300*Q

Теперь определим функцию средних переменных издержек  по формуле:

АVC = VC / Q = 0,5*Q² — 15*Q + 300

Найдём экстремум этой функции, приравняв к нулю её производную.

Q — 15 = 0

Q = 15.

При объёме производства Q = 15 средние переменные издержки будут минимальными.

АVC(15) = 0,5*15² — 15*15 + 300 = 187,5

Это так называемая точка закрытия фирмы. Фирма совершенный конкурент уйдёт с рынка, если цена упадёт ниже этой точки в краткосрочном периоде.

При Р < 187,5 фирме становится невыгодным работать на этом рынке в краткосрочном периоде.

Задача № 5. Расчёт объёма выпуска, максимизирующего прибыль фирмы

Функция издержек фирмы ТС = Q² — Q + 3, где Q — объём производства. Рыночная цена на продукцию фирмы составляет 7 и не зависит от объёма продаж этой фирмы. Найти объём выпуска продукции, максимизирующий прибыль фирмы.

Решение:

По условию рыночная цена не зависит от объёма продаж этой фирмы, это говорит о том, что фирма функционирует в условиях совершенной конкуренции.

Максимум прибыли фирмы действующей в условиях совершенной конкуренции определяется тождеством: Р = МС.

Найдём предельные издержки фирмы по формуле:

МС =(TC)’= 2Q — 1

Найдём объём выпуска продукции, максимизирующий прибыль фирмы.

Цена по условию равна Р = 7.

Р = МС

7 = 2Q — 1

Q = 4

Задача №6. Расчёт объёма производства в краткосрочном периоде

В отрасли совершенной конкуренции установилась цена Р = 30. В эту отрасль входит фирма с общими издержками ТС = 1/2 * Q² + 10 * Q + 100. Найти её объём производства в краткосрочном периоде.

Решение:

Фирма выберет такой объём производства, при котором прибыль будет максимальна. Условие максимизации прибыли: МС = MR.

На рынке совершенной конкуренции предельный доход равен цене: MR = P.

Отсюда следует, что цена равна предельным издержкам: P = MC.

Найдём предельные издержки. Предельные издержки в непрерывном случае (т.е. когда общие издержки заданы функцией) равны производной от функции общих издержек:

Функция предельных издержек будет иметь вид:

МС = Q + 10
P = MC
30 = Q + 10
Q = 20 — оптимальный объём производства фирмы.

Задача № 7. Расчёт рыночной цены и объёма выпуска на конкурентном рынке

Конкурентная фирма имеет общие затраты

ТС = 800 + 40*Q + 2*Q²

Она получает в краткосрочном периоде максимально возможную прибыль, равную 1000.

Определить цену на рынке и объём выпуска данной фирмы.

Решение:

Формула прибыли фирмы имеет вид:

П = TR — TC = P*Q — TC

По условию максимально возможная прибыль равна 1000.

P*Q — (800 + 40*Q + 2*Q²) = 1000

Найдём цену.

Условие максимизации прибыли на рынке совершенной конкуренции имеет вид:

Р = МС = MR = AR

Так как Р = МС, а МС = ТС’ = 40 + 4*Q, следовательно, Р = 40 + 4*Q. Подставим это выражение в формулу прибыли и получим:

(40 + 4*Q)*Q — (800 + 40*Q + 2*Q²) = 1000

40*Q + 4*Q² — 800 — 40*Q — 2*Q² — 1000 = 0

2*Q² = 1800

Q² = 900

Q_1,2 = ±30

Так как отрицательный корень экономического содержания не имеет, берём Q = 30.

Тогда цена будет равна:

Р = 40 + 4*30 = 160

Задача № 8. Расчёт рыночной цены на конкурентном рынке в долгосрочном периоде

Допустим, общие затраты фирмы на выпуск Q единиц продукции составляют:

Q³ – 16*Q² + 400*Q.

а) При каком значении Q средние затраты достигают минимума?

б) При какой цене этой фирме становится выгодным участвовать в совершенной конкуренции в долгосрочном периоде?

Решение:

а) Найдём функцию средних затрат по формуле:

АС = ТС / Q = (Q³ – 16*Q² + 400*Q) / Q = Q² – 16*Q + 400

Определим минимум функции. Для нахождения экстремума функции необходимо найти её производную и приравнять её к нулю.

AC’ =(Q2 – 16*Q + 400)’ = 2*Q – 16
2*Q – 16 = 0
Q = 8

При Q = 8 средние затраты достигают минимума.

б) В долгосрочном периоде фирме становится выгодным участвовать в совершенной конкуренции, если Р ≥ АС. При этом фирма имеет нулевую прибыль. И выполняется условие:

Р = МС = MR = minАС

Рассчитаем minAC. Подставим Q = 8 в функцию средних затрат:

minAC(Q=8) = 82 – 16*8 + 400 = 336

Итак, при цене Р ≥ 336 фирме становится выгодным участвовать в совершенной конкуренции в долгосрочном периоде.

Задача № 9. Расчёт цены и объёма производства, максимизирующих прибыль

Спрос на продукцию конкурентной отрасли:

Q_d = 55 – P

Предложение:

Q_s = 2P – 5

Если у одной из фирм отрасли восходящий участок кривой предельных издержек:

МС = 3Q + 5

При каких цене и объёме производства фирма максимизирует прибыль?

Решение:

Найдём цену равновесия. Приравняем функцию спроса и предложения:

Qd = Qs
55 – P = 2P – 5
3 * Р = 60
Р = 20 – цена рыночного равновесия, то есть цена по которой фирмы будут продавать свою продукцию.

Фирма в условиях совершенной конкуренции получает максимум прибыли при условии равенства цены и предельных затрат.

МС = Р
3Q + 5 = 20
Q = 5 – объём производства, при котором прибыль фирмы будет максимальной.

Задача №10. Расчёт рыночной цены и объёма выпуска на конкурентном рынке

Конкурентная фирма имеет предельные затраты:

МС = 30 + 2 × Q

при фиксированных затратах, равных 500 денежным единицам.

Она получает в краткосрочном периоде максимально возможную прибыль, равную 1100 денежным единицам.

Определить цену на рынке и объём выпуска данной фирмы.

Решение:

Формула прибыли имеет вид:

П = TR – TC = P*Q – TC

Определим функцию общих затрат. Так как функция предельных затрат это производная функции общих затрат, следовательно, функцию общих затрат можно определить как первообразную от функции предельных затрат.

где

С – константа, равная величине фиксированных затрат, которые по условию равны 500.

Таким образом функция общих затрат имеет вид:

ТС = Q² +30*Q + 500

Теперь запишем условие максимизации прибыли на рынке совершенной конкуренции в краткосрочном периоде:
Р = МС = MR = AR

Воспользуемся тем, что:

Р = МС

По условию задачи:

МС = 30 + 2 × Q, то есть Р = 30 + 2 * Q

Подставим это выражение, а так же функцию общих затрат в формулу прибыли и получим уравнение с одной неизвестной.

(30 + 2 * Q) * Q – (Q² +30*Q + 500) = 1100
Q2 = 1600
Q = ± 40

Так как отрицательное значение Q экономического смысла не имеет, следовательно, объём выпуска данной фирмы Q = 40.

Тогда рыночная цена будет равна:

Р = 30 + 2 * 40 = 110.

Методичка по решению экономических задач

(задание 17 ЕГЭ)

Составитель: Мокина В.С.,

учитель математики

МАОУ гимназия №83

Тюмень 2021 год

Содержание

l. Задачи на оптимальный выбор.

2. Задачи на кредит с аннуитетным платежом

3. Задачи на дифференцированный платеж 

4. Задачи на нахождение суммы кредита

5. Задачи на нахождение суммы вклада

Все представленные в банке ЕГЭ задачи (задание 17), можно условно разделить на группы и подгруппы:

Задачи, не связанные с банковскими операциями (задачи на оптимизацию)

Банковские задачи на вклады

1) нахождение срока вклада;

2) вычисление процентной ставки по вкладу;

3) нахождение суммы вклада;

4) нахождение ежегодной суммы пополнения вклада

Банковские задачи на кредиты:

1) нахождение количества лет выплаты кредита;

2) вычисление процентной ставки по кредиту;

3) нахождение суммы кредита;

4) нахождение ежегодного транша.

В методичке показаны методы решения задач экономического содержания, связанные с банковскими кредитами, оптимизацией производства товаров и услуг.

Рассмотрим решение задач (задание 17), в которых требуется оптимальным образом распределить производство продукции для получения максимальной прибыли.

Задачи на оптимальный выбор. Например, нужно найти максимальную прибыль (при соблюдении каких-либо дополнительных условий), или минимальные затраты. Сначала в такой задаче нужно понять, как одна из величин зависит от другой (или других). Другими словами, нужна та функция, наибольшее или наименьшее значение которой мы ищем. А затем — найти это наибольшее или наименьшее значение. Иногда — с помощью производной. А если функция получится линейная или квадратичная — можно просто воспользоваться свойствами этих функций.

У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 500 ц/га, а на втором – 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором – 500 ц/га. Фермер может продать картофель по цене 5000 руб. за центнер, а свёклу – по цене 8000 руб. за центнер. Какой наибольший доход может получить фермер?

Решение:

Величина дохода фермера будет зависеть от того как будет распределена площадь поля между картофелем и свёклой. Пусть х га, засажено картофелем на первом поле, тогда (10 – х) га, засаженных свеклой на первом поле. Полученная прибыль с первого поля, равна:

S(х) = х·500·5000 + (10 – х)·300·8000 = 24000000 + 100000х (руб.)

Функция возрастающая, т.к. к>0, значит, наибольшая доходность будет достигнута при наибольшем значении х = 10 га и прибыль с первого поля составит: S(10) = 24000000 + 100000·10 = 25000000 рублей.

Обозначим через у — количество гектар, засаженных картофелем на втором поле, а (10- у) — количество гектар, засаженных свеклой на втором поле. Прибыль со второго поля составит:

S(у) = 300·5000·у + (10 – у)·500·8000 = 40000000 – 2500000у ( руб.)

Функция убывающая, т.к. к<0, значит, наибольшая доходность будет достигнута при наименьшем значении х = 0 га и прибыль с первого поля составит: S(10) = 40000000 рублей.

Таким образом, максимальная прибыль с обоих полей, равна: S = 25000000 + 40000 = 65000000 рублей, что составляет 65 млн. рублей.

Ответ: 65млн. рублей.

Реши самостоятельно:

У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 400 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором — 400 ц/га.

Фермер может продавать картофель по цене 10 000 руб. за центнер, а свёклу — по цене 11 000 руб. за центнер. Какой наибольший доход может получить фермер?

У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 300 ц/га, а на втором — 200 ц/га. Урожайность свёклы на первом поле составляет 200 ц/га, а на втором — 300 ц/га.

Фермер может продавать картофель по цене 10 000 руб. за центнер, а свёклу — по цене 13 000 руб. за центнер. Какой наибольший доход может получить фермер?

У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 200 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 250 ц/га, а на втором — 200 ц/га.

Фермер может продавать картофель по цене 15 000 руб. за центнер, а свёклу — по цене 18 000 руб. за центнер. Какой наибольший доход может получить фермер?

Кон­серв­ный завод вы­пус­ка­ет фрук­то­вые ком­по­ты в двух видах тары — стек­лян­ной и же­стя­ной. Про­из­вод­ствен­ные мощ­но­сти за­во­да поз­во­ля­ют вы­пус­кать в день 90 цент­не­ров ком­по­тов в стек­лян­ной таре или 80 цент­не­ров в же­стя­ной таре. Для вы­пол­не­ния усло­вий ас­сор­ти­мент­но­сти, ко­то­рые предъ­яв­ля­ют­ся тор­го­вы­ми се­тя­ми, про­дук­ции в каж­дом из видов тары долж­но быть вы­пу­ще­но не менее 20 цент­не­ров. В таб­ли­це при­ве­де­ны се­бе­сто­и­мость и от­пуск­ная цена за­во­да за 1 цент­нер про­дук­ции для обоих видов тары.

Пред­по­ла­гая, что вся про­дук­ция за­во­да на­хо­дит спрос (ре­а­ли­зу­ет­ся без остат­ка), най­ди­те мак­си­маль­но воз­мож­ную при­быль за­во­да за один день (при­бы­лью на­зы­ва­ет­ся раз­ни­ца между от­пуск­ной сто­и­мо­стью всей про­дук­ции и её се­бе­сто­и­мо­стью).

5) Фаб­ри­ка, про­из­во­дя­щая пи­ще­вые по­лу­фаб­ри­ка­ты, вы­пус­ка­ет блин­чи­ки со сле­ду­ю­щи­ми ви­да­ми на­чин­ки: ягод­ная и тво­рож­ная. В дан­ной ниже таб­ли­це при­ве­де­ны се­бе­сто­и­мость и от­пуск­ная цена, а также про­из­вод­ствен­ные воз­мож­но­сти фаб­ри­ки по каж­до­му виду про­дук­та при пол­ной за­груз­ке всех мощ­но­стей толь­ко дан­ным видом про­дук­та.

Для вы­пол­не­ния усло­вий ас­сор­ти­мент­но­сти, ко­то­рые предъ­яв­ля­ют­ся тор­го­вы­ми се­тя­ми, про­дук­ции каж­до­го вида долж­но быть вы­пу­ще­но не менее 15 тонн. Пред­по­ла­гая, что вся про­дук­ция фаб­ри­ки на­хо­дит спрос (ре­а­ли­зу­ет­ся без остат­ка), най­ди­те мак­си­маль­но воз­мож­ную при­быль, ко­то­рую может по­лу­чить фаб­ри­ка от про­из­вод­ства блин­чи­ков за 1 месяц.

Предприниматель купил здание и собирается открыть в нём отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера «люкс» площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 981 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» — 4000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своём отеле предприниматель?

Решение:

Пусть у — число номеров «люкс», а  х — число стандартных номеров и S = 981м2. Тогда должно соблюдаться неравенство: 27х + 45у = 981

Выразим число обычных номеров т.е.

х = 981 – 45у, х = = 36 + = 36 +

Найдем решение этого уравнения подбором, где х, у N

Если у = 2, то х = 33 у = 14, то х = 15

у = 5, то х = 28 у = 17, то х = 8

у = 11, то х =18 у = 20, то х = 3

f(х,у) = 2000х + 4000у.

Очевидно, что максимальная прибыль будет при максимальном числе номеров «люкс», поэтому выбираем у = 20, х = 3.

Тогда в сутки предприниматель получит:

4000·20 + 2000·3 = 80000 + 6000 = 86000 рублей.

Проверим оставшиеся варианты

2·4000 + 33·2000 = 74000 рублей

5·4000 + 28·2000 = 76000 рублей

11·4000 + 18·2000 = 74000 рублей

2·4000 + 33·2000 = 80000 рублей

14·4000 + 15·2000 = 86000 рублей

17·4000 + 8·2000 = 84000 рублей

Ответ: 86000 рублей

Реши самостоятельно:

Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 30 квадратных метров и номера «люкс» площадью 40 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 940 квадратных метров. Предприниматель может определить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 4000 рублей в сутки, а номер «люкс» — 5000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?

Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 21 квадратный метр и номера «люкс» площадью 49 м2. Общая площадь, которую можно отвести под номера, составляет 1099 м2. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» — 4500 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?

Предприниматель купил здание и собирается открыть в нём отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера «люкс» площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 981 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2200 рублей в сутки, а номер «люкс» — 4000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своём отеле предприниматель?

Производство некоторого товара облагалось налогом в размере t0 руб. за ед. товара. Государство увеличило налог в 2.5 раза (t1= 2.5t0), но сумма налоговых поступлений не изменилась. На сколько процентов государству следует изменить налог, чтобы добиться максимальных налоговых сборов. если известно, что при налоге равном t руб. за ед. товара, объем производства товара составляет 9000 – 2t ед., если это число положительно, и 0 единиц?

Решение:

Обозначим Q(t) = 9000- 2t единиц товара, Q(t)- объем производства. Тогда налоговые сборы составляют S(t) = Q ·t, S(t) = (9000 — 2t)·t = 9000t – 2t2 руб. Рассмотрим функцию S(t) = 9000t – 2t2. Это квадратичная функция, графиком является парабола, ветви которой направлены вниз. Максимального значения эта функция достигает в вершине параболы. t = t = = 2250, 2250 руб. за единицу товара. При t= t0 налоговые сборы составляют 9000t0 – 2t02 руб. При t= 2,5t0 налоговые сборы составляют 9000·2,5t0 – 2·(2,5t0)2 = 22505t0 – 12,5t02 руб. Так как сумма налоговых поступлений не изменилась, то 9000t0 – 2t02 = 22505t0 – 12,5t02 / : t0 0 получим 9000 – 2t0 = 22505 – 12,5t0 , 10,5 t0 = 13500, t0 = 13500: 10,5 = , значит за единицу товара был налог руб., а стал руб. Теперь этот налог надо уменьшить на r%, чтобы налог стал равным 22500 руб. за единицу товара.

Значит государству необходимо на 30% уменьшить налог, чтобы добиться максимальных налоговых сборов.

Ответ: уменьшить на 30%

Решить самостоятельно

Производство некоторого товара облагалось налогом в размере t0 руб. за ед. товара. Государство увеличило налог в 2.5 раза (t1= 2.5t0),но сумма налоговых поступлений не изменилась. На сколько процентов государству следует изменить налог, чтобы добиться максимальных налоговых сборов. если известно, что при налоге равном t руб. за ед. товара, объем производства товара составляет 7000–2t ед., если это число положительно, и 0 единиц?

Производство некоторого товара облагалось налогом в размере t0 рублей за единицу товара. После того как государство, стремясь нарастить сумму налоговых поступлений, увеличило налог вдвое (до 2t0 рублей за единицу товара), сумма налоговых поступлений не изменилась. На сколько процентов государству следует изменить налог после такого увеличения, чтобы добиться максимальных налоговых поступлений, если известно, что при налоге, равном t рублей за единицу товара, объём производства составляет 10 000 – 2t единиц и это число положительно?

lll. 1. В начале 2001 года Алексей приобрел ценную бумагу за 11 000 рублей. В конце каждого года цена бумаги возрастает на 4 000 рублей. В начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счет. Каждый год сумма на счете будет увеличиваться на 10%. В начале каждого года Алексей должен продать ценную бумагу, чтобы через 15 лет после покупки этой бумаги сумма на счете была наибольшей?

Решение:

Используем арифметическую прогрессию, в которой а1=11000 — цена за бумагу в первый год покупки году, d=4000 — увеличение стоимости бумаги, аn — пока еще неизвестный нам год продажи бумаги (по счету от года покупки), n — номер года.

Формула n-ого члена арифметической прогрессии: an=a1+d(n-1).

Используя ее находим числа, отвечающие за стоимость бумаги на начало n-го года (по счету от года покупки).

Каждый год сумма на счете будет увеличиваться на 10% = 0,1 от данной суммы, и эти 10% должны быть больше или равны 4000.

Составим неравенство: 0,1·(a1+d(n-1)) ≥ 4000.

Подставим а1=11000, d=4000 и решим неравенство:

0,1·(11000+4000(n-1)) ≥ 4000 обе части неравенства умножим на 10, чтобы избавится от десятичной дроби, получим

11000+4000(n — 1) ≥ 40000;

11000+4000n — 4000 ≥ 40000;

4000n ≥ 33000;

n ≥ 8,25, n ∈Ν ⇒ n=8

через 8 лет надо продать бумагу, т.е. в 2001+8=2009 году

Или рассуждаем так: на восьмом году (т.е. в 2008) 10% от стоимости будет больше 4000, значит бумагу надо продать в следующем (т.е. 2009)).

Ответ: 2009 год.

Другое решение этой задачи.

Чтобы извлечь наибольшую прибыль, Алексей должен воспользоваться банковским депозитом, когда 10% от суммы, вырученной за ценную бумагу, превысит 4000 руб. Найдем значение суммы, от которой 10% будут равны 4000, получим: х·0,1 = 4000

х = 4000: 0,1 = 40000

То есть ценную бумагу в 11000 рублей нужно довести до суммы большей или равной 40000 рублей и полученную сумму положить в банк. Ценная бумага дойдет до этого уровня через 40000 – 11000 = 4000·n

n = 29000: 4000 = 7,25 n ∈Ν ⇒ n=8

то есть через 8 лет, и в начале 2009-го года полученную сумму нужно положить на банковский депозит.

Ответ: 2009.

Реши самостоятельно:

В начале 2001 года Алексей приобрел ценную бумагу за 7000 рублей. В конце каждого года цена бумаги возрастает на 2000 рублей. В начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счет. Каждый год сумма на счет будет увеличиваться на 10%. В начале какого года Алексей должен продать ценную бумагу, чтобы через пятнадцать лет после покупки этой бумаги сумма на банковском счете была наибольшей?

В начале 2001 года Алексей приобрел ценную бумагу за 19000руб. В конце каждого года цена бумаги возрастает на 3000 руб. В начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счет. Каждый год сумма на счете будет увеличиваться на 10%. В начале какого года Алексей должен продать ценную бумагу, чтобы через пятнадцать лет после покупки этой бумаги сумма на банковском счете была наибольшей?

Решение экономических задач: банки, проценты, кредиты.

1. Аннуитетный платеж – представляет собой равные ежемесячные платежи, растянутые на весь срок кредитования. В сумму платежа включены: часть ссудной задолженности и начисленный процент. При этом, в первые месяцы (или годы) кредита большую часть транша составляют проценты, а меньшую – погашаемая часть основного долга. Ближе к концу кредитования пропорция меняется: большая часть транша идет на погашение «тела» кредита, меньшая – на проценты. При этом общий размер платежа всегда остается одинаковым.

Задачи на кредит с аннуитетным платежом

1 января 2015 года Александр Сергеевич взял в банке 1,1 млн. рублей в кредит. Схема выплаты кредита следующая – 1-го числа каждого следующего месяца банк начисляет 1% на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Александр Сергеевич переводит в банк платёж. На какое минимальное количество месяцев Александр Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс. рублей?
Решение:

Ответ: 5 месяцев

Реши самостоятельно:

1 января 2015 года Иван Сергеевич взял в банке 1 млн. рублей в кредит. Схема выплаты кредита следующая: 1-го числа каждого следующего месяца банк начисляет 2% на оставшуюся сумму долга (то есть увеличивает долг на 2%), затем Иван Сергеевич переводит в банк платёж. На какое минимальное количество месяцев Иван Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 200 тыс. рублей.

1 января 2015 года Андрей Владимирович взял в банке 1,1 млн. рублей в кредит. Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 3 процента на оставшуюся сумму долга (то есть увеличивает долг на 3%), затем Андрей Владимирович переводит в банк платёж. На какое минимальное количество месяцев Андрей Владимирович может взять кредит, чтобы ежемесячные выплаты были не более 220 тыс. рублей?

1 ян­ва­ря 2019 года Павел Васильевич взял в банке 1 млн. руб­лей в кре­дит. Схема вы­пла­ты кре­ди­та сле­ду­ю­щая: 1 числа каж­до­го сле­ду­ю­ще­го ме­ся­ца банк на­чис­ля­ет 1 про­цент на остав­шу­ю­ся сумму долга (то есть уве­ли­чи­ва­ет долг на 1%), затем Павел Васильевич пе­ре­во­дит в банк платёж. На какое ми­ни­маль­ное ко­ли­че­ство ме­ся­цев Павел Васильевич может взять кре­дит, чтобы еже­ме­сяч­ные вы­пла­ты были не более 125 тыс. руб­лей?

1 ян­ва­ря 2018 года Тимофей Ильич взял в банке 1,1 млн. руб­лей в кре­дит. Схема вы­пла­ты кре­ди­та сле­ду­ю­щая — 1 числа каж­до­го сле­ду­ю­ще­го ме­ся­ца банк на­чис­ля­ет 2 про­цен­та на остав­шу­ю­ся сумму долга (то есть уве­ли­чи­ва­ет долг на 2%), затем Тимофей Ильич пе­ре­во­дит в банк платёж. На какое ми­ни­маль­ное ко­ли­че­ство ме­ся­цев Тимофей Ильич может взять кре­дит, чтобы еже­ме­сяч­ные вы­пла­ты были не более 220 тыс. руб­лей?

IV.1. 31 декабря 2014 года Алексей взял в банке 9282000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%) затем Алексей переводит в банк X рублей. Какой должна быть сумма X, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за 4 года)?

Решение:

Пусть S = 9282000 рублей  размер взятого в банке кредита. 31 декабря каждого года размер кредита увеличился на 10%, а затем, Алексей переводит в банк X рублей, т.е. остаток через четыре года будет равен нулю.

Решим уравнение: ((1,12 S – 1,1х –х)1,1 – х)1,1 – х = 0

1,14 S – 1,13 х — 1,12 х — 1,1х –х = 0

Х =

Х =

Х = 2928200

Ответ: 2928200.

31 декабря 2018 года Роман взял в банке 8599000 рублей в кредит под 14% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга(то есть увеличивает долг на 14%), затем Роман переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Роман выплатил долг тремя равными платежами (то есть за 3 года)?

31 декабря 2019 года Виктор взял в банке 3276000 рублей в кредит под 20 % годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20 %), затем Виктор переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Виктор выплатил долг тремя равными платежами (то есть за 3 года)?

31 декабря 2020 года Георгий взял в банке 2648000 рублей в кредит под 10 % годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10 %), затем Георгий переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Георгий выплатил долг тремя равными платежами (то есть за 3 года)?

IV.2. В августе 2020 года взяли кредит. Условия возврата таковы:

— каждый январь долг увеличивается на r %;

— с февраля по июль необходимо выплатить часть долга. Кредит можно выплатить за три года равными платежами по 56 595 рублей, или за два года равными платежами по 81 095 рублей. Найдите r.

Решение:

Пусть S рублей сумма кредита, ежегодные выплаты x руб., r % годовых,

к = 1 + r/100. Выплаты: b = 81095 руб., х = 56595 руб. По условию долг на июль меняется так:

Если долг выплачен двумя равными платежами b руб., то (кS – b)к – b = 0

к2 S – кb — b = 0; к2 S = (к + 1)b; S = ((к+1) b)/к2

Если долг выплачен тремя равными платежами х руб., то

((кS – х)к – х)к – х = 0

к3 S – к2 х – кх — х = 0

S = ((к2 + к+1) х)/к3

Решим систему уравнений

=

(к+1)к b = х(к2 + к+1)

(к2 + к) b = х(к2 + к) + х

(к2 + к) b — х(к2 + к) – х = 0

(к2 + к)( b – х) –х = 0

(81095 – 56595) (к2 + к) – 56595 = 0

24500к2 + 24500к — 56595 = 0

100к2 + 100к – 231 = 0

D = 102400, к = 1,1 к = -21 не удовлетворяет условию

к = 1 + r/100, r = 10%

Ответ: 10

Реши самостоятельно:

31 декабря 2017 года Пётр взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на а %), затем Пётр переводит очередной транш. Если он будет платить каждый год по 2 592 000 рублей, то выплатит долг за 4 года. Если по 4 392 000 рублей, то за 2 года. Под какой процент Пётр взял деньги в банке?

В августе 2017 года взяли кредит. Условия возврата таковы:

— каждый январь долг увеличивается на r %;

— с февраля по июль необходимо выплатить часть долга.

Кредит можно выплатить за три года равными платежами по 38 016 рублей, или за два года равными платежами по 52 416 рублей.

Найдите r.

В августе 2020 года взяли кредит. Условия возврата таковы: — каждый год долг увеличивается на r — процентов с февраля по июнь необходимо выплатить часть долга Кредит можно выплатить за 4 года равными платежами по 777600 руб. или за 2 года равными платежами по 1317600 руб. Найдите r.

В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:

— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.

Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.

2. Дифференцированный платеж – представляет собой неравные ежемесячные транши, пропорционально уменьшающиеся в течение срока кредитования. Наибольшие платежи – в первой четверти срока, наименьшие – в четвертой четверти. «Срединные» платежи обычно сравнимы с аннуитетом. Ежемесячно тело кредита уменьшается на равную долю, процент же насчитывается на остаток задолженности. Поэтому сумма транша меняется от выплаты к выплате. Если в задаче присутствуют слова «равными платежами» или «долг уменьшается на одну и ту же величину», то речь идет о дифференцированном платеже.

V. Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заёмщика возрастает на 25 % по сравнению с началом года. В конце 1-го и 2-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 3-го и 4-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заёмщика превысит 9 млн. рублей.

Решение:

Пусть S млн. рублей сумма первоначального кредита. В середине каждого года действия кредита долг возрастает на 25 %, x млн.рублей заёмщик выплачивает в конце 3-го и 4-го годов. В конце 1-го и 2-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному.

В сумме за 2 года он погашает сумму 0,25S + 0,25S = 0,5S.

В последние два года (3-й и 4-й) сумма долга сначала возрастает в 1,25 раза, а затем, погашается равными долями в x млн.рублей.

На конец 4-го года, сумма долга составляет 0 рублей. Отсюда получаем

1,252 S — 1,25 х –х = 0,

1,252 S — 2,25 х = 0, х = =

За 4 года сумма выплат составила 0,5S + 2х. По условию общая сумма выплат превышает 9 млн. рублей, то есть, 0,5S + 2>9, 4,5S + 12,5S > 81,

17S > 81, S > 4 . При минимальном целом значении S = 5 это неравенство выполняется, следовательно, размер кредита составил 5 млн. рублей.

Ответ: 5 000 000

Реши самостоятельно:

Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заемщика возрастает на 20% по сравнению с началом года. В конце 1-го и 2-го годов заемщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 3-го и 4-го годов заемщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заемщика превысит 10 млн. рублей.

Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заемщика возрастает на 25% по сравнению с началом года. В конце 1-го и 2-го годов заемщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 3-го и 4-го годов заемщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заемщика превысит 5 млн. рублей.

Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заемщика возрастает на 15% по сравнению с началом года. В конце 1-го и 2-го годов заемщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 3-го и 4-го годов заемщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заемщика превысит 7 млн. рублей.

Планируется  выдать  льготный  кредит  на  целое  число  миллионов  рублей  на  четыре года. В середине каждого года действия кредита долг заёмщика возрастает на 10 %  по сравнению  с  началом  года. По договоренности с  банком в конце 1-го и 3 – го года заемщик выплачивает только проценты  по  кредиту, начисленные  за  соответствующий  текущий  год.  В  конце  2‐го  и  4‐го  годов  заёмщик  выплачивает  одинаковые  суммы,  погашая  к  концу  4‐го  года  весь  долг  полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заёмщика превысит 100 млн. рублей. 

Планируется выдать льготный кредит на целое число миллионов рублей на пять лет. В середине каждого года действия кредита долг заемщика возрастает на 10% по сравнению с началом года. В конце 1-го и 2-го и 3-го годов заемщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заемщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наибольший размер кредита, при котором общая сумма выплат будет меньше 8 млн. рублей.

Решение банковских задач на нахождение суммы кредита

VI. В июле 2026 года планируется взять кредит в банке на три года в размере S млн. руб., где S — целое число. Условия его возврата таковы:

— каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

-в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Найдите наибольшее значение S, при котором каждая из выплат будет меньше 4 млн. рублей.

Решение:

Долг перед банком (в млн. рублей) на июль каждого года должен уменьшаться до нуля следующим образом: S; 0,8S; 0,5S; 0

По условию, в январе каждого года долг увеличивается на 25%, значит, долг в январе каждого года равен: 1,25S; 1,25∙0,8S; 1,25∙0,5S

Следовательно, выплаты с февраля по июнь каждого года составляют:

1,25S — 0,8S = 0,45S 1,25∙0,8S — 0,5S = 0,5S 1,25∙0,5S – 0 = 0,725S

По условию, каждая из выплат должна быть меньше 4 млн. рублей. Это будет верно, если максимальная из выплат меньше 4 млн.рублей, т. е.

0,725S< 4; S< 6,4 S = 6

Наибольшее целое решение этого неравенства – число 6. Значит, искомый размер кредита 6 млн. рублей.

Ответ: 6 млн. рублей.

Реши самостоятельно:

В июле 2026 года планируется взять кредит в банке на три года в размере S млн. руб., где S — целое число. Условия его возврата таковы:

— каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

-в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Найдите наименьшее значение S, при котором каждая из выплат будет больше 5 млн. рублей.

В июле 2020 года планируется взять кредит в банке на три года в размере S млн. руб., где S — целое число. Условия его возврата таковы:

— каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

-в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей.

В июле планируется взять кредит в банке в размере S тыс. рублей (S – натуральное число) сроком на 3 года. Условия возврата кредита таковы: ‐ каждый январь долг увеличивается на 22,5% по сравнению с концом предыдущего года; ‐ в июне каждого года необходимо выплатить одним платежом часть долга; ‐ в июле каждого года величина долга задается таблицей

Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей.

В июле 2016 года планируется взять кредит в банке на четыре года в размере S млн. рублей, где S — целое число. Условия его возврата таковы:

— каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Найдите наибольшее значение S, при котором общая сумма выплат будет меньше 50 млн. рублей.

В июле 2016 года планируется взять кредит в банке на четыре года в размере S млн. рублей, где S — натуральное число. Условия его возврата таковы:

— каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Найдите наименьшее значение S, при котором общая сумма выплат будет составлять целое число миллионов рублей.

Решение банковских задач на нахождение суммы вклада

VII. 15-го января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Известно, что в течении первого года кредитования нужно вернуть банку 466,5 тыс. руб. Какую сумму планируется взять в кредит?

Решение:

Обозначим через Х размер кредита, взятого в банке. Во втором месяце долг увеличивается на 3% и, затем, осуществляется выплата так, чтобы долг уменьшался на одну и ту же величину, т.е. в первый раз выплата будет составлять , и сумма долга во втором месяце составит:

1,03х – () = х — = . Аналогично для следующего месяца, только долг теперь будет составлять получаем остаток долга в размере

1,03· – () = — = .

Вторая выплата будет равна:

Аналогично третья выплата:

Аналогично четвертая выплата: и т.п.

………………………………………………………..

12- тая выплата:

Сумма выплат за первые 12 месяцев составит:

… + 13) =

В скобках получилась арифметическая прогрессия сумму, которой находим по формуле =

= + = = .

По условию в течении первого года нужно выплатить 466,5 тыс. руб.

= 466,5 Х= Х= 600 тыс. руб. или это 600000 руб.

Ответ: 600000 руб.

Реши самостоятельно:

15-го января планируется взять кредит в банке на 20 месяца. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Известно, что за первые 10 месяцев нужно вернуть банку 1179 тыс. руб. Какую сумму планируется взять в кредит?

15-го января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Известно, что за последние 12 месяцев нужно вернуть банку 1597,5 тыс. руб. Какую сумму планируется взять в кредит?

15-го января планируется взять кредит в банке на 16 месяца. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 4% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Известно, что за первые 8 месяцев нужно вернуть банку 900 тыс. руб. Какую сумму планируется взять в кредит?

5-го января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Какую сумму следует взять в кредит, чтобы общая сумма выплат после полного его погашения равнялась 1 млн рублей?

5)15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Известно, что в течение второго года кредитования нужно вернуть банку 339 тыс. рублей. Какую сумму нужно вернуть банку в течение первого года кредитования?

VIII. 15-го января планируется взять кредит в банке на 26 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца с 1- го по 25 – й месяц долг должен быть на 40 тыс. руб. меньше долга на 15-е число предыдущего месяца.

— к 15 – му числу 26 – го месяца кредит должен быть полностью погашен.

Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1924 тыс. руб.

Решение:

Обозначим через S исходную сумму кредита. В течение первого месяца эта сумма возрастает на 3%, становится равной S+0,03S = 1,03 S. Выплату нужно сделать так, чтобы исходная сумма S уменьшилась на 40 тыс. рублей, то есть, нужно выплатить

0,03S+40 тыс. рублей.

Оставшаяся сумма S-40 в следующем месяце снова увеличивается на 3%, становится равной 1,03(S-40), и следует выплатить0,03(S-40) + 40 тыс. руб., Таким образом, в течении 25-ти месяцев, сумма выплат составит:

0,03S+40 + (0,03(S-40) + 40) + (0,03(S-2·40) + 40) + (0,03(S-2·40) + 40) +… + (0,03(S-24·40) + 40) = 0,03S·25 + 40·25 – 0,03·40·( 1 + 2 + 3 +… + 24) =

S24 = 1 + 2 + 3 +… + 24 =   24 = 25·12 = 300

= 0,75 S + 1000 – 360 =0,75 S + 640

В последний 26-й месяц выплачивается остаток  1,03(S -25·40) = 1,03(S – 1000)

В сумме за 26 месяцев имеем: 0,75 S + 640 +1,03(S – 1000). По условию общая сумма выплат после полного его погашения составит 1924 тыс. руб. Составим и решим уравнение: 0,75 S + 640 +1,03(S – 1000) = 1924

1,78 S = 1924 + 390

S = 2314/ 1,78

S = 1300 тыс.руб.

Ответ: 1300000 руб.

Реши самостоятельно:

15-го де­каб­ря пла­ни­ру­ет­ся взять кре­дит в банке на 11 ме­ся­цев. Усло­вия воз­вра­та та­ко­вы:

— 1-го числа каж­до­го ме­ся­ца долг воз­рас­та­ет на 3% по срав­не­нию с кон­цом преды­ду­ще­го ме­ся­ца;

— со 2-го по 14-е число каж­до­го ме­ся­ца не­об­хо­ди­мо вы­пла­тить часть долга;

— 15-го числа каж­до­го ме­ся­ца с 1-го по 10-й долг дол­жен быть на 80 тысяч руб­лей мень­ше долга на 15-е число преды­ду­ще­го ме­ся­ца;

— к 15-му числу 11-го ме­ся­ца кре­дит дол­жен быть пол­но­стью по­га­шен.

Какой долг будет 15-го числа 10-го ме­ся­ца, если общая сумма вы­плат после пол­но­го по­га­ше­ния кре­ди­та со­ста­вит 1198 тысяч руб­лей?

15-го де­каб­ря пла­ни­ру­ет­ся взять кре­дит в банке на сумму 300 тысяч руб­лей на 21 месяц. Усло­вия воз­вра­та та­ко­вы:

— 1-го числа каж­до­го ме­ся­ца долг воз­рас­та­ет на 2% по срав­не­нию с кон­цом преды­ду­ще­го ме­ся­ца;

— со 2-го по 14-е число каж­до­го ме­ся­ца не­об­хо­ди­мо вы­пла­тить часть долга;

— 15-го числа каж­до­го ме­ся­ца с 1-го по 20-й долг дол­жен быть на одну и ту же сумму мень­ше долга на 15-е число преды­ду­ще­го ме­ся­ца;

— 15-го числа 20-го ме­ся­ца долг со­ста­вит 100 тысяч руб­лей;

— к 15-му числу 21-го ме­ся­ца кре­дит дол­жен быть пол­но­стью по­га­шен.

Най­ди­те общую сумму вы­плат после пол­но­го по­га­ше­ния кре­ди­та.

15-го декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:

— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тысяч рублей меньше долга на 15-е число предыдущего месяца;

— к 15-му числу 21-го месяца кредит должен быть полностью погашен.

Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1604 тысяч рублей?

Ответы:

1) 84 млн. руб., 2) 69 млн. руб., 3) 90 млн. руб., 4)53500 руб., 5) 2685000 руб.

1) 125000 руб., 2)104500 руб. 3)86600 рублей.

1) 2 2) 25

III. l. 1) 2008 2) 2005

1) 6 месяцев 2) 6 месяцев 3) 9 месяцев 4) 6 месяцев

IV.1. 1) 3703860 рублей 2) 155520 рублей 3) 1064800 рублей

IV.2. 1) 20% 2) 20% 3) 20% 4) 10%

1) 6 млн. руб., 2) 3 млн. руб., 3) 5 млн. руб., 4) 77 млн. руб.,

5 млн. руб.

VI. 1) 11млн.руб. 2) 200 тыс. руб. 3) 400 тыс. руб. 4) 36 млн.руб.

5) 8 млн.руб.

VII. 1) 1200000руб. 2) 3000000 руб. 3) 1200000руб. 4) 0,8 млн. руб.

5) 411000 руб.

VIII. 1) 200000 руб. 2) 384000 руб. 3) 1100000 руб.

Используемая литература:

Шестаков С.А. ЕГЭ 2017. Математика. Задачи с экономическим содержанием. Задачи 17(профильный уровень)/Под ред.И.В.Ященко.-М.:МЦНМЩ, 2017

30 тренировочных вариантов ЕГЭ под редакцией И. В. Ященко» – 2021.

В задании №17 в ЕГЭ по профильной математике, вместо ожидаемой текстовой задачи на кредиты, иногда встречаются оптимальный выбор. Этот вид задач считается более сложным по сравнению с кредитами. Чтобы хорошо подготовиться к экзамену, нужно научиться их решать.

Тут требуется умение искать наибольшие и наименьшие значения функции, обычно зависящей от нескольких переменных. Эти переменные, как правило, связаны дополнительными условиями.

Вам обязательно понадобится умение искать производные и исследовать функции на экстремумы. Нужно знать, что такое ограниченные, возрастающие и убывающие функции. Если вы умеете решать 12-й и 7-й номера из ЕГЭ, то вам повезло – все необходимое для решения инструменты уже у вас в руках. А те, кто не умеет считать производные, то настоятельно рекомендуем сначала разобраться с первой частью экзамена и только потом переходить на более сложные задачи, такие, как №17.

Основной подход к решению заключается в следующем. Необходимо составить функцию, задающую нужную зависимость – если нужно найти максимальную или минимальную прибыль, значит это должна быть функция, описывающая прибыль, если нужен максимальный выпуск продукции на заводе, значит функция должна задавать количество продукции выпускаемой заводом, нужно найти оптимальное расстояние – наша функция будет описывать расстояние. Внимательно, функция может зависеть сразу от нескольких переменных. После того, как вы смогли записать функцию, нам предстоит ее исследовать.

На самом деле, тут нет какой-то сухой теории, которую можно прочить и научиться решать задачи на оптимальный выбор. Поэтому давайте учиться на примерах. Сначала разберем простые, поймем алгоритм решения, а потом перейдем к более сложным, которые могут встретиться на экзамене.

Пример 1

Пусть у Василия есть завод, который выпускает спичечные коробки. Расходы на производство одного коробка 1 руб, а продает он их за 5 руб. В итоге с каждого коробка Василий получает прибыль 4 руб. Давайте разберемся, сколько нужно производить коробков, чтобы прибыль была наибольшей, если (Х) работников завода может производить в месяц ( N=-left(x-10right)^{2}+500) коробков.

И так, согласно условию задачи, если на заводе Х работников, то они производят ( N=-left(x-10right)^{2}+500) коробков.

А какая прибыль (P) с такого количества? Ответ очевиден, нужно просто прибыль (4 руб) с одного коробка умножить на количество произведенных коробков: ( P=4*(-left(x-10right)^{2}+500)).

Давайте посмотрим при каком количестве работников прибыль Василия будет максимальна. Или другими словами при каком (Х) будет наибольшим (Р). Такое задание часто встречается в 12-м номере ЕГЭ, нужно просто исследовать нашу зависимость прибыли ( P=4*(-left(x-10right)^{2}+500)) от (Х) и найти экстремумы.

Напомню, что функция принимает наибольшее или наименьшее значения в точках, где ее производная равна 0. Значит ищем производную от (Р) и приравниваем к 0.

$${P}^{’}=(4*(-left(x-10right)^{2}+500))^{‘}= 4cdotleft(-2right)cdotleft(x-10right)$$

Приравниваем (0):

$$4cdotleft(-2right)cdotleft(x-10right)=0$$

И ищем (Х), при котором производная равна (0):

$$ X=10.$$

Что мы такое нашли? При этом значении (Х) (количестве рабочих) прибыль будет либо максимальна, либо минимальна. Это точка экстремума, а какая именно, мы пока не знаем.

Давайте это определим. Напоминаю, если производная отрицательная, то функция убывает, если положительна, то возрастает. Если подставить значения меньшее (10) в нашу производную, например (1):

$$ 4cdotleft(-2right)cdotleft(x-10right) = 4cdotleft(-2right)cdotleft(1-10right)=4*18=72$$

Значение производной получилось больше 0:

$$ {P(x<10)}^{‘}>0$$

Значит при (Х<10) функция возрастает, а при (Х>10) убывает. А значит (Х=10) – это максимум. Мы получили, что максимальная прибыль будет, если на производстве будет задействовано всего 10 рабочих. Как так может быть? Казалось бы, чем больше рабочих, тем больше продукции выпускает завод, а значит и больше прибыль. Но в реальной жизни все не так просто – размеры завода ограничены, и если там будет слишком много людей, то они просто будут мешать друг другу делать свою работу, в результате выпуск продукции начнет снижаться или поднимутся расходы на производство.

Вернемся к задаче, а какая будет максимальная прибыль? Просто подставим (Х=10) в функцию для прибыли:

$$ P=4*(-left(x-10right)^{2}+500)= 4*(-left(10-10right)^{2}+500)=4*500=2000 руб. $$

Только что мы решили первую задачу на оптимальный выбор.

Разберем следующий пример:

Пример 2

Пусть опять у нас есть завод, на котором расходы на производство (y) автомобилей составляет (Q=0,5y^2+y+7) миллионов рублей в месяц. Если продавать каждый автомобиль за (S) тысяч рублей, то при продаже всех произведенных за месяц автомобилей завод получит доход (S*y), а заработает на этом прибыль (доходы минус расходы) — (S*y-Q). Какую наименьшую цену продажи (S) нужно установить, чтобы за 3 месяца завод получил прибыль 75 миллионов рублей?

Первым делом давайте составим функцию, описывающую зависимость прибыли от количества произведенной продукции и цены продажи, которую мы должны установить. Сразу 2 неизвестные!

И так, чтобы посчитать прибыль (P(y,S)), зависящую от (у) и (S), нам нужно стоимость продажи одного автомобиля (S) умножить на количество проданных машин (у), получим общий доход, и вычесть все расходы (Q), которые мы понесли при производстве (в условии, кстати, это написано — подсказка):

$$P(x,S)=S*y-Q=S*y-(0,5*y^2+y+7)=-0,5y^2+(S-1)y-7$$

Проанализируем полученное выражение. Это квадратный многочлен. Если построить график относительно (у), то это уравнение параболы. Как анализировать квадратные многочлены, можно посмотреть тут.

Так как коэффициент перед (y^2) отрицательный, то ветки параболы направлены вниз. То есть, наибольшее значение нашей функции будет в вершине параболы. Можно по известным формулам найти вершину и значение функции и в ней, это и будет максимальное значение. А можно пойти по старому пути, как в примере 1, и посчитать производную. Число (S) будем считать просто за константу, то есть берем производную относительно (у):

$$ {P(x,S)}^{’}={(-0,5y^2+(S-1)y-7)}^{’}=-y+S-1; $$

Приравниваем производную нулю, чтобы найти точки экстремума:

$$-y+S-1=0;$$
$$y=S-1;$$

Так как график исходной функции парабола с ветками вниз, то это точка максимума функции (P(x,S)). Подставим (y=S-1) в нашу функцию:

$$ P(x,S)=-0,5*y^2+(S-1)y-7=-0,5(S-1)^2+(S-1)(S-1)-7=frac{(S-1)^2}{2}-7; $$

Мы получили — какую максимальную прибыль мы можем заработать в зависимости от (S). Другими словами, подставляя различные значения стоимости автомобиля в нашу функцию, получим максимальную прибыль при данной стоимости продажи.

По условию задачи общая прибыль за 3 месяца должна быть не меньше чем 75 миллионов рублей. Запишем это в виде неравенства:

$$ {3*P(S)}_{max}=3*frac{(S-1)^2}{2}-7 ge 75; $$

Осталось только решить это неравенство:

$$(S-1)^2ge64;$$
$$(S-9)(S+7)ge0;$$

(S) отрицательным быть не может, что это тогда за бизнес, где цена продаваемой продукции отрицательна. А значит при (S ge9) прибыль завода будет больше 75 миллионов рублей.

Пример 3

Решим задачу на оптимизацию расстояния:

Два мотоциклиста подъезжают к перекрестку по двум перпендикулярным дорогам. Первый едет со скоростью 40 км/ч и до перекрестка ему осталось ехать 5 км, а скорость второго 30км/ч и ехать до перекрестка 3 км. Через какое время расстояние между мотоциклистами будет наименьшим?

Для решения задачи нам понадобится теорема Пифагора, ведь мотоциклисты едут по взаимно перпендикулярным дорогам, а значит расстояние между ними — это гипотенуза прямоугольного треугольника, а катеты – это расстояния от каждого мотоциклиста до перекрестка.

Пусть мотоциклисты уже находятся в пути (t) часов. Тогда первый проедет расстояние:

$$S=v*t=40t;$$

До перекрестка осталось ехать

$$S_1=5-40t;$$

А второму:

$$S_2=3-30t;$$

Мы получили прямоугольный треугольник с катетами (S_1) и (S_2). По теореме Пифагора выведем функцию, задающую расстояние между мотоциклистами:

$$L=sqrt{(5-40t)^2+(3-30t)^2}=sqrt{25-400t+1600t^2+9-180t+900t^2}=sqrt{2500t^2-580t+34};$$

Согласно условию задачи, нужно найти такое время (t), чтобы расстояние (L) было наименьшим. Для этого опять возьмем производную и исследуем функцию (L) на экстремум:

$$ {L}^{’}=frac{1}{2*sqrt{2500t^2-580t+34}}*(5000*t-580); $$

Приравниваем нулю:

$$5000*t-580=0;$$
$$t=frac{580}{5000}=frac{29}{250} часа;$$

Так как при (t) меньшем этого числа производная функции отрицательна, а при большем – положительна, то получаем точку минимума и, что расстояние между мотоциклистами будет наименьшим через (frac{29}{250}) часа, это и требовалось найти.

Если бы в задаче нас попросили еще найти это расстояние, то нужно подставить (t=frac{29}{250}) в функцию расстояния (L):

$$L(t=frac{29}{250})=sqrt{(5-40*frac{29}{250})^2+(3-30*frac{29}{250})^2}=(frac{3}{5})км$$