|
Есть 10 мешков, полные монет. В девяти из них — все монеты из чистого золота, а в одном мешке — все монеты фальшивые. Известно, что фальшивая монета весит на один грамм меньше золотой. Как при помощи только одного взвешивания на циферблатных весах определить, в каком из мешков находятся фальшивые монеты? Во первых нужно пронумеровать мешки от 1 до 10, и из каждого мешка взять столько монет, сколько соответствует его номеру, из первого 1-ну, из второго 2-ве и т.д. из десятого 10 всего 55 штук. Если бы все монеты были настоящими, их вес был бы 110 грамм (при условии что настоящая весит 2 грамма, а фальшивка 1 грамм). на сколько грамм меньше будут весить мешок(вместо 110 грамм) можно определить фальшивый мешок. если на грамм ,то 1-й мешок, если на 5 грамм, то 5-й мешок и т.д. система выбрала этот ответ лучшим Татьяна100 6 лет назад Я больше практик, чем теоретик, поэтому если бы сама попала в такую ситуацию, то обходилась бы вообще без весов. Ведь если следовать математическому методу и из каждого мешка брать по 1, 2, 3 монеты и т.д., то общее количество монет будет 55. Весы в условиях задачи — циферблатные, т.е. никаких двух чаш там нет — можно только узнать точный вес. А ведь взвешивать можно только ОДИН раз (может весы после этого сразу ломаются или батарейки садятся — не знаю), но если вы даже высчитали, что фальшивки например в 9 мешке, то как вы ПОТОМ из этих 55 монет найдете эти 9 фальшивых уже без взвешивания? Поэтому я бы расставила эти мешочки в ряд по объему (на взгляд) — от маленького к большому. Потом в самом маленьком и пересчитала монеты, запомнила цифру. Далее в каждом мешке оставила бы столько же монет — остальные лежали бы кучкой рядом с этим мешочком. Когда в каждом мешочке оказалось бы по одинаковому количеству монет, определить самый легкий было бы не трудно — ведь каждая сотня монет, это уже разница в 100 грамм, а тысяча — уже килограмм. Конечно, долго пересчитывать, но золото требует терпения. fatalex 8 лет назад Вообще, в этой задаче не хватает данных Какие весы используются ( с одной чашей или с двумя ) ? Если весы двухчашечные и при этом показывают разницу в граммах, то… нумеруем мешки, как предложил Владимир и выкладываем на левую чашу 1 монету из первого мешка, 2 из второго, 3 из третьего, 4 из четвертого и 5 из пятого. На правую чашу 1 монету из шестого мешка, 2 из седьмого, 3 из восьмого, 4 из девятого и 5 из десятого. Если легче левая чаша весов, то разница в весе укажет количество фальшивых монет на весах и номер мешка с фальшивыми монетами, а если легче правая чаша, то номер мешка с фальшивками равен разнице веса монет плюс 5. Так, если правая чаша легче на 4 грамма, то фальшивки в 4 плюс 5 = 9-том мешке. Если же весы с одной чашей, то нужно еще знать массу фальшивой или настоящей монеты. Допустим настоящая весит 5.2 грамма. Выкладываем на весы монеты так, как предложил Владимир. Если бы все монеты были настоящими, то на весах была бы масса 55 * 5.2 = 286 грамм, но т.к. в одном мешке монеты легче, то и весы в итоге покажут меньшую массу, а отличие полученной массы монет от эталонных 286 грамм укажет нам на номер мешка с фальшивыми монетами. Допустим фальшивки в 7 мешке. Значит на весах окажется 7 фальшивых монет и 48 настоящих. Масса монет на весах составит 5.2 * 48 плюс 4.2 * 7 = 249.6 плюс 29.4 = 279 грамм. Проверяем: 286 — 279 = 7 Фальшивки в 7-ом мешке и на весах их 7 штук. Пы.Сы. пишу «плюс» прописью потому, что значок плюс со смартфона, с которого я пишу ответ, почему-то отображается здесь в виде пробела Колючка 555 3 года назад Видела как то я эту задачу, только монеты были серебряными и весили 5 грамм, а фальшивые 4 грамма. От этих цифр давайте и отталкиваться. Из первого мешка берем 1 монету, из 2 две и так далее. Всего 55 монет. Их вес должен быть 275 грамм, если бы все были золотыми. А так как в одном из мешков фальшивка, то и вес будет меньше. Если на весах 270 грамм, то фальшивые монеты в 5 мешке. Также и другие мешки можно вычислить. Galina7v7 7 лет назад Главное — определить отличие в общем весе монет от эталонного.и на сколько граммов.Все мешки нумеруются.и из каждого берется столько монет-какой номер мешка.Монет будет 55.(1+2+3+4+5+…9+10=55)Пусть настоящие монеты весят по 2 г.а фальшивые по 1 г.Правильный вес должен быть =110 г.Но он будет отличаться на 1.2.3…10 г.И вот сколько г.не будет хватать.под тем номером и будет мешок с фальшивыми монетами. Даксплячи Учлинзайх 7 лет назад Тут уже давали вариант что из первого мешка одну монету берем, из второго две и т.д. Хотя можно конечно и попроще задачку решить Главное что бы в мешках было одинаковое количество монет Взвесьте мешки — мешок с фальшивыми монетами будет весить меньше, чем остальные мешки Но это только в том случае, если в мешках одинаковое количество монет Ну и разумеется должны быть хорошие весы МарияСС 6 лет назад Нам необходимо сначала разделить мешки на 2 части по 5 мешков, далее (из каждой части) взять из первого мешка одну монету, из второго — 2 и так далее. Всего мы возьмем 30 монет. Часть из них фальшивая и весит на один грамм меньше. Нам необходимо определить сколько точно монет фальшивых, тогда мы сможем выяснить номер мешка, в котором находятся поддельные монеты. Нужны для этого нам чашечные весы. На сколько граммов одна кучка монет будет легче другой, такой и порядковый номер мешка из той части, в которой оказались более легкие монеты. Korobok 10 лет назад Насчёт немцев — не знал, это любопытно. Что же до задачи, то, думаю, Владимир решил правильно, но лишь наполовину. Принцип тот же, только мешки надо разделить поровну, по 5 штук и кучки монет от каждой партии разложить на разные чаши весов. Количество делений ( граммов ), на которые отклонится стрелка от нуля, и укажет на искомый мешок. Трифон Ли 10 лет назад В детстве читал эту задачу. О ней такая история. Во время 2 мировой немцы разбросали над Англией листовки с этой задачей. Цемцы посчитали, что нанесли этим ущерб английской экономике, т.к. на решение казалось бы простой задачи люди потратили уйму рабочего времени. Если бы цемцы не были такими наивными они тогда еще изобрели комп. chela 10 лет назад Нумеруем мешки. Из мешков в последовательности берем 1,2,3 … 10 монет. Всего будет 55 монет. Взвешиваем их и получаем вес, например m и разделим его на 55. Получим целое число и дробь. Теперь запишем (1-дробь)*55=№ нужного нам мешка. Для решения этой задачи нужны очень точные весы, желательно аптечные. Максим Костенко 10 лет назад А на кой ляд тут вообще весы? Каждая фальшивая монета весит на грамм меньше. В мешке с фальшивыми монетами их тысячи. Мешок с фальшивыми монетами будет на килограммы легче. Знаете ответ? |
Смотрите также
-
- © 2014 — 2023 «Game 🏃 Runs» — прохождения видеоигр
- Отказ от ответственности
- Правообладателям
- Постеры игр: © MobyGames.com
- Полезное
I.

Давайте представим, что мы попали
на Дикий Запад. В маленьком американском городке орудует банда грабителей.
Все мы будем сыщиками и наша задача – найти и обезвредить преступников. Мы
сумеем это сделать, если правильно выполним все задания. Шериф городка узнал,
что готовится ограбление банка, значит, его надо охранять. Для охраны
помещения квадратной формы шериф позвал четырех охранников. Шериф решил
поставить у
каждой стены банка по одному охраннику, но сначала подошло только 2
охранника. Как они должны встать?
Затем подошел еще один охранник. Как теперь встанут три охранника?

наконец, пришел четвертый охранник. Какова теперь будет расстановка
охранников?
Потом осторожный шериф решил еще более усилить охрану так, чтобы у каждой
стены было по два охранника, но новых охранников он решил не звать. Как он
должен расставить охрану?
Молодцы, вы очень помогли шерифу, хорошо справились с задачами. В чем
заключалось их решение?
То есть для решения задачи, сводящейся к ответу на вопрос «как
сделать что-либо?», достаточно предъявить конкретную конструкцию,
соответствующую требованиям задачи.
Бандиты, ничего не подозревая о такой усиленной охране, ворвались в
банк и были арестованы. Причем, Билла арестовали раньше Гарри, Джона – позже
Гарри, Джека – раньше Билла, а Тома – позже Джона. Известно, что главаря
банды арестовали раньше всех. Кто же главарь? Напишите имена арестованных по
порядку.
(Задание выполняется поэтапно, то есть исследуется каждая фраза
предложения).

Кого арестовали позже всех?
Кто был арестован позже Гарри?
Итак, банда во главе с Джеком арестована. На допросе они рассказали
шерифу, где спрятаны награбленные ими сокровища, там был проведен тщательный
обыск. У бандитов изъяли 4 крупных драгоценных камня: красного и зеленого
цветов, причем красных камней было больше, чем зеленых. Сколько камней
каждого цвета было у бандитов?
Круглый золотой браслет бандиты успели распилить на 3 части. Сколько
было сделано распилов?
Почему получились разные ответы? Какой из них все-таки правильный?
В чем же была ошибка у тех, кто сказал два распила?
Слиток золота весит полкилограмма и еще полслитка. Сколько весит
целый слиток?
На столе лежали серебряные кольца: два слева, одно справа; два
справа, одно слева; одно в центре и два с краю. Сколько было колец?
У бандитов было три золотых пластины. Одну из них они разрезали
пополам. Сколько пластин у них изъяли?
А еще у них было 3 серебряных круглых браслета. Один из них распилили
пополам, то есть сделали два разреза. Сколько браслетов стало?
Опять получились разные ответы. Давайте выясним, почему и какой
правильный.
У бандитов изъяли два одинаковых по весу кольца: одно золотое, другое
серебряное. Какое из них стоит дороже?
Еще у них нашли пару старинных часов. В начале обыска они показывали
5 часов, а через полчаса одни показывали полшестого, а другие – без
пятнадцати шесть. Какие часы испорчены?
Молодцы, это была задача на внимание. Также у бандитов нашли
бриллианты. В одной кучке было пять бриллиантов. Когда один бриллиант
переложили во вторую кучку, в них стало бриллиантов поровну. Сколько камней
было во второй кучке первоначально?
У бандитов нашли три старинные монеты. Известно, что одна из них
фальшивая – она легче настоящих. Как найти фальшивую монету с помощью
взвешивания на чашечных весах без гирь. Чашечные весы – это просто две
чашечки, подвешенные на палочке или лежащие на основании. Главное свойство
таких весов: они всего лишь определяют, какой из лежащих на чашках предметов
тяжелее, но не определяют, на сколько тяжелее, и не измеряют вес предмета.
Что мы можем наблюдать?
За сколько взвешиваний мы нашли фальшивую монету?
Придумайте название этой задаче.
Задачи на «фальшивые монеты». Так называется целый блок задач.
Сегодняшнее занятие мы посвятим рассмотрению таких задач. Попробуйте
сформулировать цель и тему занятия.
II.
Содержательная часть
Хорошо, перейдем к решению следующей задачи.
Задача. Найдите фальшивую монету из 9,если известно, что она легче
настоящей.
 |
|||||
 |
 |
||||
Есть ли другие способы решения?
Как эту задачу свести к предыдущей?
Итак, мы нашли два способа решения задачи. Сравните их. За сколько
взвешиваний мы нашли фальшивую монету, решая задачу первым способом?
То есть в общем случае три. При решении таких
задач нельзя ограничиваться рассмотрением лучшего случая, а надо
рассматривать все возможные случаи.
Сколько взвешиваний нам потребовалось при втором способе решения?
Поэтому первое решение более рациональное. Оформлять будем следующим
образом:
А Б В
Каждую кучку монет обозначим А, Б и В. Пусть
на весы положены кучки А и Б. Будем обозначать это действие так: А,
Б. Следующий шаг и возможные случаи будем обозначать стрелкой. Чтобы
различать монеты каждой группы будем ставить номер с индексом, например: 1А, 1Б, 2В
и т. д. Если чаши весов в равновесии будем писать знак равенства (=). Если
груз тяжелее, то знак >, к примеру, запись А>Б означает, что кучка А
тяжелее кучки Б.
А, Б
А=Б А<Б А>Б
1В, 2В 1А,
2А 1Б, 2Б
1В=2В 1В <2В 1В
>2В … …
3В 1В 2В
Оформлять решение, конечно, следует самым
рациональным способом. Но очень часто в условии задач «на фальшивые монеты»
сразу указано наименьшее из возможных число взвешиваний, необходимых для
решения, как, например, в следующей задаче.
Задача. Требуется за три взвешивания на чашечных весах без гирь
найти среди 6 монет одну фальшивую, при этом неизвестно, тяжелее она настоящей
или легче, но известно, что она имеет другую массу.
Обозначим монеты на перетянувшей чаши А и Б, а на второй через В и Г.
Напомним, что монеты А и Б могут быть либо настоящими, либо более тяжелыми,
чем настоящие, а монеты В и Г – либо настоящими, либо более легкими, чем
настоящие.
Сравните эту задачу с предыдущими?
Какие, на ваш взгляд, более сложные?
Почему?
Нужно было показать на рисунке (или описать словами) расположение
охраны.
Сначала, согласно первой фразе текста, появляется последовательность
имен: Билл, Гарри. Затем, Билл, Гарри, Джон. Третья фраза дает
последовательность: Джек, Билл, Гарри, Джон. Наконец, последняя фраза:
Джек, Билл, Гарри, Джон и Том.
Джек – главарь банды.
Тома.
Джон и Том.
3 красных и 1 зеленый.
2.
3.
Правильный ответ – 3
распила.
Они спутали круг с отрезком: чтобы разделить на 3 части
отрезок нужно 2 распила, а круг – 3.
1 кг, так как полслитка весит 0,5
кг.
Было три кольца.
Изъяли 4 пластины.
2.
4.
Правильный ответ – 2 браслета, так как после распила третьего
браслета просто не стало. А пластина даже после распила осталась пластиной.
Золотое, так как золото стоит дороже серебра.
Вторые, так как через полчаса они стали показывать 45 минут, то есть
ушли вперед на 15 минут.
3 бриллианта.
Поместим на каждую чашку по монете.
1. Если одна чашка весов выше другой, значит, монета на ней легче и,
следовательно, она является фальшивой.
2. Если обе чашки весов стоят ровно, то есть вес этих двух монет
одинаков, поэтому ни одна из них не может быть фальшивой.
Вывод: фальшивой является оставшаяся монета, та, которую не клали на
весы.
За одно.
Задача на «фальшивые монеты», на взвешивание и т. д.
Цель занятия: научиться решать задачи на «фальшивые монеты».
Тема занятия: Задачи на «фальшивые монеты».
Можно разложить монеты на 3 кучки: 4, 4 и 1 монета. Положим первые 4
монеты на одну чашу, другие на вторую.
1.
Если чаши весов
находятся в равновесии, то фальшивая отложенная монета.
2.
Если одна чаша выше
другой, значит, на ней фальшивая, более легкая, монета (одна из четырех).
Разделим их еще на 2 кучки по 2 монеты в каждой и опять положим на весы.
Остаться в равновесии чаши не могут, так как на одной находится фальшивая
монета. Две монеты на перетянувшей чаше настоящие. На другой еще одним
взвешиванием найдем фальшивую.
Разделим монеты на 3 кучки по 3 монеты. Положим на первую чашу весов
одну кучку, на вторую – другую.
Если чаши остались в равновесии, то фальшивая монета среди оставшихся
трех. Если одна чаша выше другой, то фальшивая монета среди трех, находящихся
на ней. Теперь нужно найти фальшивую монету из трех, а это делать мы уже
умеем (предыдущая задача).
За одно взвешивание в лучшем случае, за три в худшем.
В любом случае два взвешивания.
Также, как и в предыдущих задачах, поделим монеты на три кучки по две
монеты. Две из них положим на чаши весов: если весы в равновесии, то
фальшивая монета среди двух отложенных. Сравним каждую из отложенных монет с
настоящей (еще два
взвешивания), найдем фальшивую и определим, легче или тяжелее она,
чем настоящая. Если одна из чашек перетянет, то фальшивая среди монет на
весах, а отложены настоящие монеты. Положим теперь на левую чашу весов А и В,
а на другую – монету Б и одну хорошую монету из отложенных. Если весы в
равновесии, то монета Г – фальшивая, она легче настоящей. Если перетянула
левая чаша, то фальшивая она тяжелее настоящей. Если перетянет правая
чаша, то возможны два случая: фальшивая и более легкая монета В, или
фальшивая и более тяжелая монета Б. Оставшимся третьем взвешиванием сравним В
с хорошей монетой. В случае равновесия Б – фальшивая. Если хорошая монета
перетянет, то фальшивая В.
Задачи на нахождение неизвестного по двум разностям
Рассмотрим задачи, в которых по двум разностям (одна из которых известна) находят неизвестное. Такие задачи имеют два варианта решения.
Задача 1. Купили 7 синих ручек и 4 красных ручки по одинаковой цене. За синие ручки заплатили на 138 рублей больше, чем за красные ручки. Сколько стоят синие ручки и сколько красные?
Данную задачу можно записать в виде таблицы:
| Цена одной ручки | Кол-во ручек | Стоимость | |||
|---|---|---|---|---|---|
| Синие | ? | одинаковая | 7 | ? | 138 р. |
| Красные | ? | 4 | ? |
Решение: По условию задачи нам известна одна разность стоимости синих и красных ручек — 138 рублей. Мы можем найти ещё одну разность – на сколько больше купили синих ручек, чем красных:
7 — 4 = 3 (руч.).
Теперь по этим двум разностям можно узнать цену одной ручки:
138 : 3 = 46 (р.) — цена одной ручки.
Теперь, зная цену одной ручки, найдём сначала стоимость синих ручек, а потом красных:
46 · 7 = 322 (р.) — стоимость синих ручек,
46 · 4 = 184 (р.) — стоимость красных ручек.
Стоимость красных ручек можно было найти и по другому, вычесть из стоимости синих ручек их разность в цене с красными ручками:
322 — 138 = 184 (р.).
Таким образом, задачу на нахождение неизвестного по двум разностям можно решить двумя способами:
| 1-й способ: | 2-й способ: |
|---|---|
| 1) 7 — 4 = 3 (руч.) | 1) 7 — 4 = 3 (руч.) |
| 2) 138 : 3 = 46 (р.) | 2) 138 : 3 = 46 (р.) |
| 3) 46 · 7 = 322 (р.) | 3) 46 · 7 = 322 (р.) |
| 4) 46 · 4 = 184 (р.) | 4) 322 — 138 = 184 (р.) |
Ответ: Синие ручки стоят 322 рублей, а красные ручки — 184 рубля.
Задача 2. В среду привезли 6 мешков картошки, а в четверг — 10 таких же мешков. Масса мешков с картошкой, привезённых в среду, на 140 кг меньше, чем масса мешков с картошкой, привезённых в четверг. Найти массу картошки за среду и за четверг.
Данную задачу можно записать кратко с помощью таблицы:
| Масса мешка | Кол-во мешков | Общая масса | |||
|---|---|---|---|---|---|
| среда | ? | одинаково | 6 | ? | 140 |
| четверг | ? | 10 | ? |
Решение: Разность в массе между мешками с картошкой, привезённых в среду и четверг, нам известна — 140 кг. Можно найти ещё одну разность — на сколько больше мешков привезли в четверг, чем в среду:
10 — 6 = 4 (меш.).
Теперь по двум данным разностям можно узнать массу одного мешка:
140 : 4 = 35 (кг).
Затем, зная массу одного мешка картошки, можно найти массу мешков, привезённых в среду:
35 · 6 = 210 (кг).
Массу мешков с картошкой, привезённых в четверг, можно найти двумя способами: первый способ — умножить массу одного мешка на количество мешков:
35 · 10 = 350 (кг).
Второй способ — прибавить к массе мешков, привезённых в среду, 140 кг (именно на столько меньше они весят, чем мешки, привезённые в четверг):
210 + 140 = 350 (кг).
Таким образом, у этой задачи два способа решения:
| 1-й способ: | 2-й способ: |
|---|---|
| 1) 10 — 6 = 4 (меш.) | 1) 10 — 6 = 4 (меш.) |
| 2) 140 : 4 = 35 (кг) | 2) 140 : 4 = 35 (кг) |
| 3) 35 · 6 = 210 (кг) | 3) 35 · 6 = 210 (кг) |
| 4) 35 · 10 = 350 (кг) | 4) 210 + 140 = 350 (кг) |
Ответ: Масса картошки, привезённой в среду, равна 210 кг, а картошки, привезённой в четверг, — 350 кг.
Логическая задача про монеты
Логическая задача про монеты понравится всем, кто любит логику и понимает пользу головоломок для саморазвития. Если вы до сих пор не были знакомы с этой задачей, то остается только позавидовать тому удовольствию, которое вы получите от ее решения.
Сразу нужно сказать, что никаких подвохов ни в условии, ни в самом решении нет. Поэтому сосредоточившись, активируйте все свои логические способности и приступайте к поиску единственно верного и чрезвычайно изящного решения.
Условия задачи
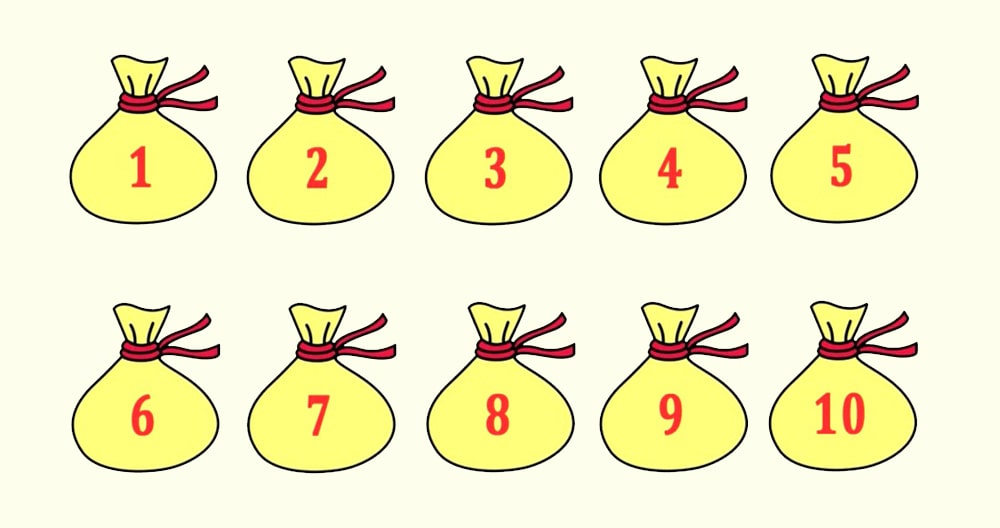
Перед нами 10 пронумерованных мешков, в каждом из которых находится по 10 золотых монет. Каждая монета весит 10 граммов.
В одном из мешков находятся фальшивые монеты. По виду они ничем не отличаются от настоящих, вот только весят они не по 10, а по 11 граммов.
Суть этой логической задачи заключается в том, чтобы при помощи весов найти мешок с фальшивыми монетами. Монеты из мешков можно сколько угодно вынимать и как угодно перекладывать. Казалось бы, дело за малым.
Но вот главное условие, которое делает задачу довольно сложной: взвешивание можно произвести только один раз.
Напомним, что данная головоломка предполагает абсолютно точное решение, поэтому не тратьте время на поиск какого-то подвоха – его тут просто нет. Решается задача исключительно при помощи логического мышления.
Делитесь в комментариях ходом своих рассуждений, чтобы любой желающий мог либо подтвердить, либо опровергнуть ваше решение.
Что же, удачи вам, и пожалуйста, не ищите готовые ответы или подсказки – используйте свои собственные способности! Наш мозг и так очень мало напрягается в современном мире, так почему бы не использовать редкую возможность размять его при помощи этой великолепной логической задачи?!
Если вам понравилась эта задача на логику – поделитесь ею с друзьями в социальных сетях. Если вам вообще нравятся логические задачи и головоломки, – подписывайтесь на сайт interesnyefakty.org. С нами всегда интересно!
Понравился пост? Нажми любую кнопку: