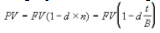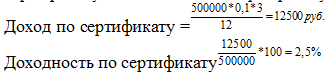Задача как найти номинал

Задача о сумме

В знаменитой задаче с монетами, которыми необходимо отсчитать сдачу, как известно, есть две беды.
— первая – это количество номиналов монет,
— вторая – это количество разрядов числа, представляющего сдачу.
И обе эти величины оказывают экспоненциальное воздействие на нагрузку машины Тьюринга, которая собственно и занимается подсчётом.
Признавать, что человек имеет сразу две зависимости, не принято даже в обществе алкоголиков. Поэтому я решил подстраховаться и избавиться от одной из этих проблем заранее. Путь это будет количество номиналов монет.

В двух словах суть проблемы описывается так: экспоненциальная зависимость. То есть выпуск нового типа монет несуществующего доселе номинала влечёт за собой увеличение количества комбинаций монет в два раза. Ещё один номинал – ещё в два раза, и так до условной бесконечности. При галопирующей инфляции, когда новые монеты/купюры выпускаются достаточно часто, для решения задачи придётся покупать более мощный компьютер. А где на это взять деньги при галопирующей то инфляции?

Итак, решение, которое на самом деле достаточно просто.
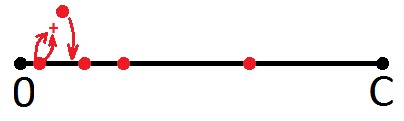
Если представить отрезок от нуля до С (сдача) с нанесёнными на ней точками, соответствующими номиналам монет, то любой интеллектуальный человек увидит примерно следующую картинку:

Ну, возможно в других цветах.
Итак, что мы можем сказать про красные точки? Конечно же то, что число, соответствующее любой этой точке, есть сумма, которую мы можем выдать в виде сдачи. Причём одной монетой. Возможно кто-то увидел что-то другое, но я, как художник, вкладывал именно этот смысл. И, как художник же, дорисую на этой картинке ещё одну точку, соответствующую сумме первой (слева направо) точки с этой же точкой (всё правильно: получится удвоенный номинал). Дорисую этим же цветом, ибо новая точка означает то же самое – эта сумма так же может быть сдачей.

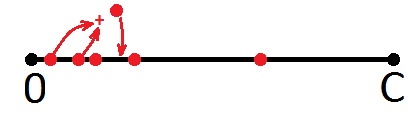
Далее беру первую точку и суммирую со второй, даже если вторая точка это предыдущая сумма (это неважно, ибо все точки здесь равны). Новую точку опять нанесу на отрезок.

Если новая точка выходит за пределы отрезка, то ничего не рисуем, а возвращаемся к началу отрезка и берём следующую точку, то есть вторую. Далее то же самое (слева направо).
Собственно, когда точка С (напомню, это сдача) станет красной, можно считать, что решение найдено. А можно пройти полный цикл и найти оптимальное решение, что бы количество монет было минимальным.

С точки зрения программирования, здесь два цикла. Первый от 0 до С/2 (нет необходимости брать первую точку большей С/2, т.к. вторая точка всегда больше первой и в сумме они выйдут за границы отрезка). Второй цикл является встроенным в первый, он начинается с той же точки, на которую указывает внешний цикл и до момента, когда сумма покинет границы отрезка.
По сути это перебор: мы не теряем ни одного варианта, и гарантированно найдём оптимальное решение, или придём к выводу, что решения нет.

Давайте подсчитаем количество итерации внутри наших циклов. По внешнему циклу – это С/2, по внутреннему – где-то столько же. Умножим С/2 * С/2 = (С^2) / 4. Округлим до С в квадрате. Это наихудший вариант, когда весь наш отрезок просто состоит из красных точек. Если же между точками будут пробелы, количество итераций значительно уменьшится.
Как видим при определении сложности решения задачи мы не используем количество номиналов монет. Эта величина напрямую совсем никак не влияет на сложность решения. Влияют величины этих номиналов, скажем монета в 1 цент и сделает этот отрезок полностью красным. Поэтому эту монету лучше и не брать в расчёт, а в конце решения взять ближайшую к С красную точку и набросать сверху одноцентовиков. Но это уже момент оптимизации алгоритма, а она за рамками этой статьи.

Вот собственно и всё, что хотелось бы сказать. Рабочую версию программы можно найти здесь: github link

1. В файле init.h задать COINS_NUMBER — количество номиналов монет, и AMOUNT — сумма сдачи.
2. В файле coinc.c указать номиналы монет в массиве coins.
3. Под Linux запустить make_sh.
4. Запустить программу app на выполнение

Приведу какой-нибудь забавный пример. Представим, что в какой-нибудь стране к власти пришли математики и ввели в обращения 32 номинала монет: 2, 3, 5, 7, 11, 13, 17, 19… 131. Для удобства счёта выбрали только простые числа (ну не смешно ли?). И, что бы убедиться, что денежная реформа прошла успешно, послали в магазине гонца разменять купюру 5333 (тоже простое число). Кассир на стареньком одноядернике решил задачу: 39 монет номиналом 131 пифагороцентов, одну монету 127 и одну 97. Расчёт занял 3 секунды и чуть больше мегабайта памяти. Правительству доложили, что народ реформой доволен, считает быстро.

И пример, который чуточку сложнее проверить. Монеты, сто номиналов в такой вот странной последовательности: 0101, 0202, 0303… 9898, 9999, 100100. Сумма сдачи: 101010. Поиск решения занял 1 секунду и чуть больше мегабайта памяти. А решения, собственно, и нет, то есть нельзя такими монетами набрать такую сумму. С этими же монетами проверка суммы в 1 миллион займёт 26 мегабайт и сотни секунд, что говорит об экспоненциальной зависимости от суммы, но не количества номиналов монет.

Задача №11 (расчет номинальной и реальной процентной ставки)

Домохозяйка имеет 100 ден. ед. и решает: сберечь их или потратить. Если она положит деньги в банк, то через год получит 112 ден. ед. Инфляция составляет 14% в год.

Необходимо определить:

1. Какова номинальная процентная ставка?
2. Какова реальная процентная ставка?
3. Какой совет следует дать домохозяйке?
4. Как повлияет на решение снижение темпа инфляции до 10% при неизменной номинальной ставке процента?

Решение:

1. Номинальная процентная ставка составляет 12% (112*100/100-100).

2. Реальная процентная ставка составляет -2% (12-14).

3. При отрицательной реальной процентной ставке целесообразно потрать деньги сейчас, так как сумма процентных поступлений не превысит рост цен на товары.

4. Если темп инфляции снизится до 10%, то реальная процентная ставка составит 2% (12-10). При положительной процентной ставке лучше сберечь деньги, положив их в банк (если, разумеется, не терпится потратить их сейчас на покупку необходимых товаров).

Тема: Задачи на экзамен по рынку ценных бумаг с решением

Раздел: Бесплатные рефераты по рынку ценных бумаг

Тип: Задача | Размер: 16.76K | Скачано: 1406 | Добавлен 08.10.09 в 20:30 | Рейтинг: +21 | Еще Задачи

Задача №1 Акции номиналом 1000 руб. продавались по рыночной стоимости 3000 руб. Объявленный дивиденд составлял 10% годовых. Определить годовую сумму дивиденда и реальную доходность акций по уровню дивиденда.

Решение:

Дгод = (1000*10%) / 100% = 100 руб.

Дрын = 100 / 3000 = 0,03 = 3,3%

Задача №2 Акции номиналом 500 руб. были куплены по цене 600 руб. в количестве 100 шт. и проданы через 3 года по цене 700 руб. за акцию. Дивиденды по акциям составили: в 1 год – 10%, во 2 год – 15%, в 3 год – 20%. Определить полученный доход по операциям.

Решение:

1) Сумма покупки акций Пок. ак. = 100*600 = 60000 руб.

2) Сумма продажи акций Пр. ак. = 100*700 = 70000 руб.

3) Сумма полученных дивидендов Д 3 года = 100*500*(0,1+0,15+0,2) = 22500 руб.

4) Общий доход равен 70000+22500-60000 = 32500 руб.

5) Дох-сть32500/60000*100%=54%

Задача №3 Акции с дивидендной ставкой 20% при номинальной стоимости 2000 руб. проданы через год по рыночной стоимости 3000 руб. Определить совокупный доход акции и доходности акции в процентах.

Решение:

Дгод = (2000*20%) / 100% = 400 руб.

Ддоп = 3000 – 2000 = 1000 руб.

Дсовок. = 1000 + 400  = 1400 руб.

Доходность акции Дакц = (1400/2000)* 100% = 70%.

Задача №4 Банк при учёте векселя на сумму 1500 тыс.руб., до срока оплаты которого осталось 45 дней, выплатил его предъявителю 530 тыс.руб. Определить учётную ставку, использованную банком, если расчётное количество дней в году составило 360.

Формула дисконтирования по учетной ставке имеет следующий вид:

где PV – выплачиваемая сумма

FV – номинал

d – учетная ставка

В – временная база = 360 дней.

учётная ставка использованная банком.

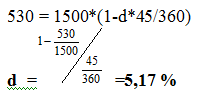
Задача №5 Вексель – срок обращения 90дней номиналом-10000, размещается под 10%годовых Определить доход =10000*0,01*90/360=25

Задача №6 Гос.облигации фед.займа номиналом 1000руб. и сроком погашения 3года продается по курсу 805руб. Какова доходность в конце срока?

Дох = (1000-805)/805 = 0,242=24,2%

Задача №7 Депозитный сертификат сроком обращения 3 месяца и доходностью 10% годовых выпущен с наминалом 500000 рублей. Определить доход по сертификату и доходность по сертификату за срок займа.

Задача №8 Депозит.сертификат со сроком обращения 6месяцев и 8%годовых доход имеет номинал 1000000руб.Определить 1)Абсолютный доход 2) Доходность сертификата на срок его обращения

1)Доход =1000000*0,08*6/12=40000руб

2) Дох-ть=40000/1000000=0,04=4%

Задача №9 Инвестор обеспокоен падением курса акций, чтобы застраховать себя от потерь покупает 100акций компании Б по курсу 96руб за акцию, и затем продает опцион кол сот сроком 1 месяц, и ценой 85руб. Общая стоимость 1700.Определить понесет ли инвестор убытки, если акция Б упадет на 79руб. Какова будет прибыль если курсовая цена акции =85руб.

1) Если падает,то (100*96)-(79*100+1700)=9600-9600=0(не теряет)

2) Если 85 и опцион исп,то 85*100+1700-100*96=10200-9600=600

Задача №10 Курсовая цена акции, которая была размещена по номиналу 1000 руб., в первый год после эмиссии составляла 1500 руб. Определить дополнительный доход и доходность акции в %, а так же совокупный доход, если величина дивиденда сост-ла 20%.

Решение:

1) Дг = (1000*20%) / 100% = 200 руб.

2) Ддоп = 1500 – 1000 = 500 руб.

3) Дсовок = 500 + 200 = 700 руб.

4) Доходность акции равна (700 / 1000) * 100% = 70%

Задача №11 Курсовая цена акций по номиналу 300руб, составляет 500руб.Определить доп.доход и дох-ть акции, а также совокупный доход, если величина дивиденда 20%?

1)Абс.величина дивиденда=300*20/100=60руб.

2)Доп.доход=500-300=200руб.

3)Совокупный доход = 200+60=260руб.

4)Совокупная дох-ть=260*100/300=86,7%

Задача №12 Наращенная стоимость облигации номиналом 500 руб. в момент погашения в полтора раза превышает ее номинал. Срок обращения облигации — 5 лет. Определить годовую купонную ставку.

Решение:

Кг = (500*1,5-500) / 500*5 = 0,1 = 10%

Задача №13 Номинал акции 600руб.Куплена 800руб.Продана 900руб.Ставка дивиденда 15%.Определить1)Величину дивиденда 2)Доп.доход 3) Совокупный доход 4)Рендит

1) Див=600*15/100=90руб.

2)Доп.доход= 800-600=200руб.

3)Совокуп.доход=200+90=290руб

4)Рендит=90/600*100=115%

Задача №14 Номинал облигации -1000 руб., котировка облигации составляет при покупке 42 %, при продаже – 44 % от номинала. Определить цену покупки, продажи и размер дисконта.

Для удобства сопоставления рыночных цен облигаций с различными номиналами в финансовой практике

используется специальный показатель, называемый курсовой стоимостью или курсом ценной бумаги. Под ним понимают текущую цену облигации в расчете на 100 денежных единиц ее номинала, определяемую по формуле:

K = ( P / N ) x 100,

где K — курс облигации;

P — рыночная цена;

N — номинал.

Согласно условию, облигация куплена по курсу 42 %, а продана за 44 % от номинала. Таким образом.

Р_{покупки} = 420 руб.

Р_{продажи} = 440 руб.

Следовательно, размер дисконта составил  20 руб. (440-420).

Задача №15 Облигация наминалом 10000 рублей была продана владельцом при 8% годовых через 170 дней после очередного дня выплаты по купону. Определить купонный доход облигации.

Дк = (10000*0,08*170дн.) / 360 дн. = 377,7 руб.

Задача №16 Облигация номиналом 1000руб.имеет купонную дох-ть 8%годовых. Определить величину годового текущего дохода?

2подхода: 1.) ф-ла точных% дох = 0,08*1000/365=21,9%

2.) ф-ла простых% дох = 0,08*1000/360 = 20%

Задача №17 Облигация номиналом1000руб продана владельцу с учетом 15%годовых через 150дней после очередного выплаты процента. Купонный доход продавца

Слож.%=1000*150*0,15/365

1000*150*0,15/365

Задача №18 Опеделите доход по векселю со сроком обращения 90дней, номиналом 10000и ставкой 10%

Доход=90*10000*0,01/360=50руб

Задача №19 Определить рыночную стоимость купонной облигации за 40 дней до погашения купона, если номинал облигации составил 1000 руб., купонный доход – 120 руб., а длительность периода между выплатами купонного дохода – 60 дней.

По условию купонный доход – 120 руб., значит ставка купона равна 120/1000 = 0,12 или 12 %.

Накопленный купонный доход на дату сделки можно определить по формуле:

,   

где CF — купонный платеж;

 t — число дней от начала периода купона до даты продажи (покупки);

 N — номинал;

k — ставка купона;

 m — число выплат в год;

 В = {360, 365 или 366} — используемая временная база (360 для обыкновенных процентов; 365 или 366 для точных процентов) (как правило, в мировой практике анализа применяют т.н. финансовый год (360 дней в году, 30 дней в месяце). Эта временная база официально установлена для расчетов процентных выплат по ОВВЗ и еврооблигациями РФ).

CF = 1000 (0,12/6) = 20 руб.

НКД =

Таким образом, рыночная стоимость купонной облигации за 40 дней до погашения купона составит 1000+ 66,67  = 1066,67 руб.

Задача №20 Определить совокупный доход и дох-ть сертификата, номиналом 10тыс.руб. размещенного под 10%годовых на 3месяца

1)Абсолютная дох-ть=1000*0,1*3/12=250руб.

2)Дох-ть=250/10000=2,5%

Задача №21 Прибыль АО «Орбита», предназначенная на выплату дивидендов, составила за год 8540 тыс.руб. Привилегированные акции составили сумму 5000 тыс.руб., что равнялось 1/10 общей суммы акций предприятий. На привилегированные акции был установлен фиксированный размер дивиденда – 20 % к номиналу. Определить средний размер дивидендов по всем акциям и сумму дивидендов по привилегированным и обыкновенным акциям.

По условию на привилегированные акции был установлен фиксированный размер дивиденда – 20 % к номиналу, значит 5000 * 20 % = 1000 тыс.руб. из прибыли было направлено на выплату дивидендов по этому виду акций.Так как привилегированные акции составляют 1/10 общей суммы акций предприятий, то значит общая сумма равна 50000 тыс.руб. (5000*10=50000).

Итак,Сумма дивидендов по привилегированным акциям => 1000 тыс.руб.

Сумма дивидендов по обыкновенным акциям => 8540-1000 = 7540 тыс.руб.

Средний размер дивидендов по всем акциям =>

8540 тыс.руб. / 50000 тыс.руб. = 0,1708 руб. в среднем выплачено на каждый рубль общей суммы акций.

Задача №22 Простой вексель сроком 90 дней на сумму 10000руб датированный на 10марта был учтен банком 5мая и учтен по 10%.Определить какую сумму получит векселедержатель и какова величина дисконта в пользу банка

Март=22дня

Апрель=30дней

Май=5дней

Итого=57дней

Сумма векселедержателя=10000*(1-57/360*0,1)=9850

Дисконт=10000-9850=150руб.

Задача №23 Рыночный курс акций компании «В» составляет 500 долл. Инвестор приобретает опцион на покупку акций 100 шт. по курсу 60 долл. Премия по опциону составляет 500 долл. Срок действия опциона – 3 месяца. Какова будет прибыль на опцион, если к концу действия опциона рыночная цена акций составит 80 долл.? Каков будет убыток инвестора, если курсовая цена акции на рынке будет равна 50 долл.?

Решение:

Доход по опциону составит:

80*100 – (60*100 +500) = 1500 долл

Чтобы полностью ознакомиться с решением задач, скачайте файл!

+21

08.10.09 в 20:30
Автор:Глушко

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Задачи на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Задачи для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Задача, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---

Похожие работы

• Тестовые задания и решение задачи по рынку ценных бумаг
• Задача: Портфель паевого инвестиционного фонда состоит из 100 акций
• Задача: Инвестор сформировал инвестиционный портфель
• Решенная задача по рынку ценных бумаг
• Решение задач по РЦБ
• Задачи с решением к экзамену по рынку ценных бумаг
• Задачи и их решение по рынку ценных бумаг
• Решение экзаменационных задач по рынку ценных бумаг
• Бесплатные задачи с решением по РЦБ
• Экзаменационные задачи по рынку ценных бумаг

Шесть куч монет одинакового номинала каждая, но все разные в кучах выложили на столе. В одной куче при подсчёте обнаружилось ровно 37 монет, во второй 26, в третьей 44, в четвёртой тоже 44, в пятой 72 монеты и в шестой 20 монет. В каких-то из куч оказались перевёрнутыми ровно по половине монет, в какой-то 25, в другой 13, в ещё в одной 15. А в одной было перевёрнуто столько монет, что их достоинство в сумме составило 40 денежных единиц. А всего в сумме было перевёрнуто монет на сумму 420. В разных кучах достоинство монет было от 1 номинала, до 10 номиналов. Какова сумма всех денег в монетах? бонус за лучший ответ (выдан): 5 кредитов Даю третий вариант своего решения. Я связался с Ирой ЛДВО на БВ и уточнил, какой именно номинал монет можно использовать для решения задачи, она указала на этот: 1к, 2к, 3к, 5к, 10к, 50к, 1р, 2р, 3р, 5р, 10р, 50р, 100р, приведу его к единым единицам, к рублям: 0.01р, 0.02р, 0.03р, 0.05р, 0.1р, 0.5р, 1р, 2р, 3р, 5р, 10р, 50р, 100р, ибо когда речь идёт о 40 единицах и 420 единицах нужно понимать одинаковые единицы — например, рубли, а не разные для 40 и 420. Далее в задаче говорится: Прямо тут не говорится, что речь идёт именно о трёх кучах, как того хочет почему-то Ирина. Хорошо, пусть будет три такие кучи, соглашусь я и с этим условием, хоть оно и не очевидно. И так, решение. Рассмотрим такую таблицу перевёрнутых монет: количество монет — номинал — сумма 40 — 1р — 40р, 25 — 10р — 250р, 15 — 2р — 30р, 13 — 3р — 39р, 10 — 5р — 50р, 22 — 0.5р — 11р, как видно, в одном случае есть требуемая сумма в 40 рублей, а общая сумма всех перевёрнутых монет равна 420 рублей. Все условия выполнены. Остаётся только сказать, из каких именно куч сделана эта выборка. 40 монет может быть только в куче 44, или в куче 72, 13 монет взяты, как половина из кучи 26, 10 монет взяты, как половина из кучи 20, а 22 монеты взяты из кучи 44. Как видите, я выполнил своё обещание, у меня как раз три кучи, где монет перевёрнутых по половине. И так определим это соотношение по кучам: перевернутые монеты — начальная куча 40 — 44, или 72 25 — ? 15 — ? 13 — 26, 10 — 20, 22 — 44, у нас осталось ещё две кучи 37 и 44. И их можно раскидать четырьмя способами: а) 40 — 44, 25 — 72, 15 — 37, 13 — 26, 10 — 20, 22 — 44, б) 40 — 44, 25 — 37, 15 — 72, 13 — 26, 10 — 20, 22 — 44, в) 40 — 72, 25 — 37, 15 — 44, 13 — 26, 10 — 20, 22 — 44, г) 40 — 72, 25 — 44, 15 — 37, 13 — 26, 10 — 20, 22 — 44, что даёт нам четыре варианта искомой суммы всех монет: 1038 рублей, 758 рублей, 730 рублей или 786 рублей соответственно. Ответ: при данном наборе допустимых номиналов монет задача не имеет единственного решения. Всё. автор вопроса выбрал этот ответ лучшим Ироха Прему­драя на БВ [45.4K] более года назад  данные про кучи и перевёрнутые монеты: 37; 26; 44; 44; 72; 20. 1/2; 1/2; 1/2; 25; 15; 13. 40 д.е. Всего 420 д.е. Единственная в этой задаче зацепка — это 40 д.е. (денежных единиц). Минимальная монета в 1 ед. Значит должно быть 20 монет перевёрнутых и 20 скрытых. Итог: 40 монет — не подходит. Минимальная монета в 1 ед. Значит должно быть 25, 15, 13 монет перевёрнутых и всего 40 монет — не подходит. Следующая монета в 2 ед. Значит должно быть 10 монет перевёрнутых и 10 скрытых. Итог: 20*2 = 40. Как раз половина — подходит. 6) Одна из перевёрнутых на половину монет куча — это последняя: 20 монет половина перевёрнута всего по 2 д.е. 40 д.е. Осталось 420 — 40 = 380 д.е. Новые данные: 37; 26; 44; 44; 72. 1/2; 1/2; 25; 15; 13. Всего 380 д.е. Максимальное число монет 72. Оно делится на 1, (2 нет), 3, 4 бывает, (6, 7, 8, 9 номинал отсутствует). Подходит по 1 все варианты. 3, 5, и тем более 10 не подходит. 37*3 = 101 >72. 5) Одна из перевёрнутых на половину монет куча — это последняя: 72 монет из 1 д.е, половина перевёрнута всего 72 д.е. Осталось 380 — 72 = 308 д.е. Новые данные: 37; 26; 44; 44. 1/2; 25; 15; 13. Осталась одна половина перевёрнутых. Это не 37. 37 нечётное число, значит там перевёрнуто или 25, 15, или 13 монет. 37 монет это предположительно пятаки. Получится 37*5 = 185 д.е. Это 4-я куча монет. 4) Перевёрнутых 13 монет. Останется 308 — 185 = 123 д.е. Новые данные: 26; 44; 44. 1/2; 25; 15. Здесь сосредоточен подвох в задаче. 44 монеты, даже если предположить, что бывают монеты в 4 д.е. 44*4 = 176 > 123 д.е. Превышен предел остатка. Но тут я вспомнила про российские деньги или американские или ещё какие. 1, 2, 3, 5 долларовые/рублёвые/­лиры/юани монеты имеются. А пол долларовых или четвертаков (50 центов, 25 центов) ещё не было. Возьму 44 монеты по полдоллара. Выйдет 22 доллара. И половина из них открыта. 3) Перевёрнутых 22 монеты. Останется 123 — 44*0,5 = 123 — 22 = 101 д.е. Новые данные: 26; 44 монет. 25; 15 перевёрнутых. Не комментировать! Ответ будет продолжен и редактироваться! Ира ЛДВО на БВ [266K] более года назад  Моё решение, но оно неверное. Мне сказали, что монет в 4 рубля не бывает. А про копейки я не додумалась. Вот оно: 1) Половина кучи из 20 монет по 4 рубля 10 монет. Итог: 4*10 = 40 рублей. Куча 20*4 = 80 руб. 2) Половина кучи из 72 монет по 1 рублю 36 монет. Итог: 36 рублей. Куча 72 руб. 3) Половина кучи из 44 монет по 2 рубля 22 монеты. Итог: 2*22 = 44 рубля. Куча 44*2 = 88 рублей. 4) 15 монет по 3 рубля из кучи в 44 монеты. Итог 15*3 = 45 руб. Куча 44*3 = 132 рубля. 5) 25 монет по 5 рублей из кучи в 26 монет. Итог 25*5 = 125 руб. Куча 26*5 = 130 рублей. 6) 13 монет по 10 рублей из кучи в 37 монет. Итог 13*10 = 130 руб. Куча 37*10 = 370 рублей. Считаю открытые монеты: 40 + 36 + 44 + 45 + 125 + 130 = 420 рублей. сходится. Всего денег. Считаю: 80 + 72 + 88 + 132 + 130 + 370 = 872 рубля. Но это число может быть другим. Это как пример. Nasos [172K] более года назад  Ох, правы Вы, Ира ЛДВО на БВ, не решить мне эту задачу. Не решить однозначно. Ибо… Если есть уже 40 денежных единиц как: 5 перевёрнутых монет номиналом 8 единиц, или 8 перевёрнутых монет номиналом 5 единиц, их можно привязать к куче в 20 монет, то достаточно взять заданных: 25 перевёрнутых монет номиналом 3 единицы, 13 перевёрнутых монет номиналом 7 единиц, 15 перевёрнутых монет номиналом 6 единиц, и (как половину из куч в 72 монеты и 26 монет) 36 перевёрнутых монет номиналом 2 единицы, 13 перевёрнутых монет номиналом 4 единицы, чтобы получить в сумме 420 единиц. А какова общая сумма всех монет, спросите Вы? А Бог его ведает, ибо, как я уже говорил 40 набирается двумя способами, а 25, 13 и 15 перевёрнутых монет можно раскидать по оставшимся кучам в 37, 44 и 44 монеты тоже многими способами. Таким образом, эта задача имеет множество решений, которые мне даже не охота просчитывать. Чепуха, а не задача, ещё и сформулирована невнятно (ну, это для уже, меня, дурака). Nasos [172K] более года назад  Хорошо, я буду допускать только номиналы 1, 2, 3, 5 и 10, но поскольку их всего пять, а мешков шесть, придётся ввести номинал 0.5, тогда имеем такую картину: количество монет — номинал — сумма 40 — 1 — 40, 25 — 10 — 250, 13 — 3 — 39, 15 — 2 — 30, 10 — 5 — 50, 22 — 0.5 — 11, итого 420 и есть заданная обязательная сумма 40. Как же они расположены по мешкам? Ясное дело, что 40 монет может быть из мешка 72, или 44. Половинки 10 и 22 взяты из мешков 20 и 44. Из остальных мешков: 26, 37 и 44, или 26, 37 и 72, можно доставать любое количество оставшихся заданных монет 25, 13 и 15 в любом их сочетании. Вариант решения не единственный. erkta­x [316] более года назад  ну если совсем уж честно ответить то я хз) Знаете ответ?

Номинальная и эффективная ставка процентов

Краткая теория

---

В практике распространен вариант схемы
сложных процентов, когда капитализация вклада (начисление процентов) происходит несколько раз в году:
ежемесячно, поквартально, раз в полгода, а то и ежедневно. На практике очень
часто при этом в условиях сделки оговаривается не ставка процента за период
начисления, а годовая ставка процента j и период начисления, например, «20%
годовых с ежемесячным начислением процентов». Оговариваемая в контракте годовая
ставка процента j называется номинальной ставкой и служит для определения ставки
процента за период начисления. Пусть j − номинальная ставка, m − число
начислений в году, тогда ставка процента за период начисления находится по
простым процентам, и равна

.

За

 лет будет

 начислений,
поэтому наращенная сумма составит:

Процентные начисления за

 лет
составят:

А процентные начисления за год:

Последняя формула – формула
действительной или эффективной ставки процента. Эта ставка измеряет тот
реальный относительный доход, который получают в целом за год от начисления
процентов, то есть служит мерой доходности сделки по схеме сложных процентов.
Эффективная ставка при

 больше номинальной, в при

.

Замена в договоре номинальной ставки j при m-разовом
начислении процентов на эффективную ставку

 не изменяет финансовых обязательств участвующих
сторон, то есть обе ставки являются эквивалентными ставками процента в финансовом отношении.

Финансовые
сделки различаются по длительности и по схемам расчета платежей:

простые процентные ставки

и

сложные процентные ставки,
простые и сложные учетные ставки, номинальные
процентные и учетные ставки и т. д. Чтобы иметь возможность сравнивать
эффективность сделок, осуществленных по разным схемам, используют эффективную
ставку процентов, дающую тоже соотношение между начальным капиталом

 и конечным

, что и принятая схема. Если известны платежи по простой операции и срок
сделки, то находим выражение для определения эффективной ставки:

Кроме понятий номинальной и эффективной процентной ставки, в банковской учете используются понятия номинальная и эффективная учетная ставка.

Примеры решения задач

---

Задача 1

Сумма
размером

 тысяч рублей инвестирована на

 лет по ставке

 годовых. Найдите наращенную за это время сумму
и ее приращение при начислении процентов:

а)
ежегодно;

б) по
полугодиям;

в)
ежеквартально;

г)
ежемесячно.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Наращенную сумму долга можно найти
по формуле:

 -число
начисления процентов в году

 -число полных
лет

а) при начислении процентов
ежегодно:

:

Приращение суммы составит: 

б) при начислении процентов по
полугодиям:

Приращение суммы составит: 

в) при начислении процентов
ежеквартально:

Приращение суммы составит: 

г) при
начислении процентов ежемесячно:

Приращение суммы составит: 

Ответ:

а)

; 

  

б)

; 

 

в)

; 

 

г)

; 

---

Задача 2

Определить
номинальную годовую процентную ставку, если эффективная ставка равна 28% и
сложные проценты начисляются ежеквартально

Решение

Эффективную
ставку можно найти из формулы:

Откуда
номинальная годовая ставка:

В
нашем случае

 (ежеквартальное начисление процентов)

Получаем:

Ответ:

---

Задача 3

Вычислить эффективную ставку процента, если банк начисляет и
капитализирует проценты ежемесячно исходя из номинальной ставки 40% годовых.

Решение

Эффективную ставку процента
можно найти исходя из следующего равенства:

Откуда искомая эффективная
ставка:

В нашем случае:

 –
банк начисляет проценты ежемесячно

 

Ответ: