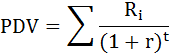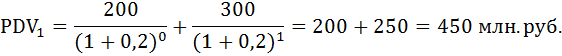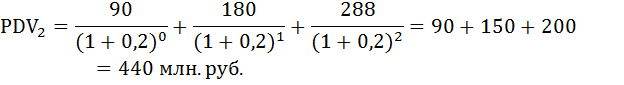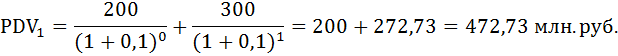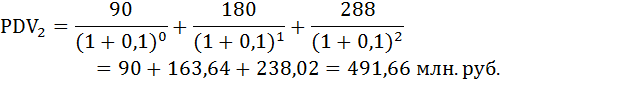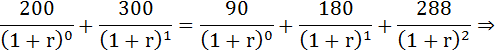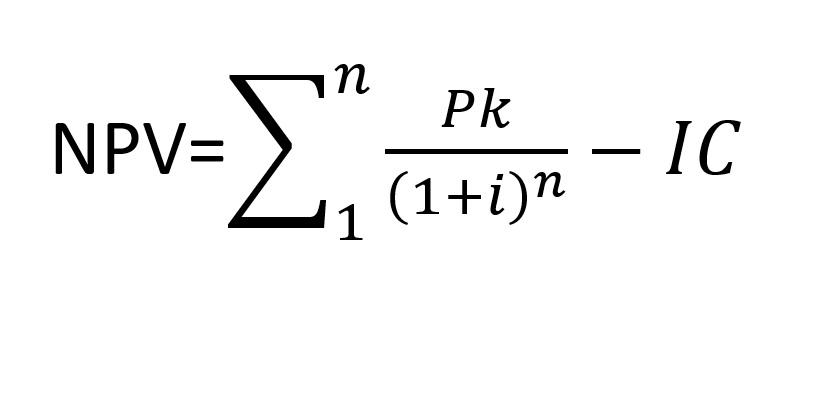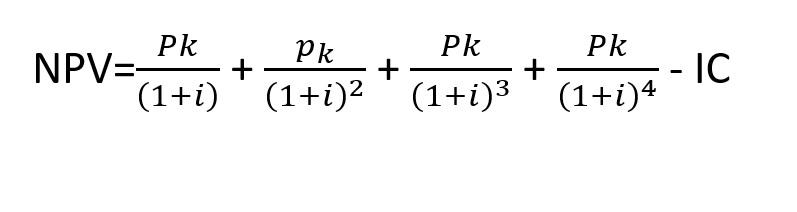Задача как найти приведенную стоимость

Две фирмы предлагают проекты строительства дома отдыха. Первая берётся построить его за два года и просит в первом году 200 млн р., а в начале второго – 300 млн р. Вторая фирма нуждается в трёхлетних инвестициях: 90, 180 и 288 млн р. в начале каждого года соответственно.

а) Какой из этих проектов дешевле, если для сравнения использовать 20 %-ную ставку дисконтирования? Найти приведённые стоимости проектов.

б) Какой из этих проектов дешевле, если для сравнения использовать 10%-ную ставку дисконтирования? Найти приведённые стоимости проектов.

г) Найти так называемую уравнивающую ставку дисконтирования, при котором ни одному из проектов нельзя отдать предпочтение.
 

Решение:

Рубль сегодня больше чем рубль через год. Поэтому затраты равные одному рублю сегодня больше, чем затраты, равные одному рублю завтра. Для того чтобы узнать общую сумму затрат за несколько периодов времени, необходимо привести затраты за ряд периодов (лет) в эти проекты к одному моменту времени.

а) Пусть r = 20%. Найдём приведённую стоимость проектов по формуле:

При ставке дисконтирования равной 20% проект второй фирмы оказался дешевле.

б) Пусть r = 10%. Найдём приведённую стоимость проектов:

При ставке дисконтирования 10% первый проект оказался дешевле.

в) Найдём уравнивающую ставку дисконтирования. Для этого решим уравнение:

r = 0,1621 или 16,21%.

Приведенную стоимость рассчитывают с целью определения сегодняшней цены инвестиций, доход от которых будет получен в будущем периоде. То есть, показатель отражает текущую стоимость активов с учетом доходности.

Понятие приведенной стоимости

Приведенная стоимость (далее ПД) представляет собой значение доходности вложений на сегодняшний день. Если говорить простыми словами, приведенная стоимость – это объем денежных средств, которые инвестор получит в будущем периоде, переведенный в стоимость на сегодняшний день.

Кроме понятия «приведенная стоимость», в экономике существует такой термин, как «чистая приведенная стоимость» (далее ЧПД). ЧПД – это совокупность финансовых оборотов от вложений, переведенных в стоимость на момент проведения анализа.

Чистая приведенная стоимость отличается от ПД тем, что при определении первого показателя учитываются первоначальные финансовые вложения. То есть, сумма, которую компания инвестировала для получения дохода, отнимается из будущей стоимости актива, приведенной к значению на сегодняшний день.

Зачем рассчитывают приведенную стоимость

Приведенную стоимость рассчитывают с целью определения объема денежных средств, которые инвестор получит в будущем в стоимостной оценке на дату проведения анализа. Например, сегодня компания вложила 1 млн. рублей в развитие проекта. Неизвестно, сколько предприятие получит от реализации программы. Однако данное значение можно вычислить при помощи формулы расчета приведенной стоимости.

Как правило, в будущем денежные средства имеют совсем иную цену, в сравнении с днем сегодняшним. А особенностью вычисления приведенной стоимости считается тот факт, что анализ отражает сумму дохода в стоимости на сегодняшний день. Для этого будущий доход дисконтируется.

Расчет приведенной стоимости

Расчет приведенной стоимости значительно отличается от вычисления будущей доходности. Для того, чтобы вычислить приведенную стоимость, для начала, необходимо найти будущую доходность. Именно от этой суммы отталкивается аналитик, производящий анализ. Будущая стоимость в дальнейшем приводится к сегодняшнему значению путем дисконтирования.

Важно! Результат расчета приведенной стоимости показывает не сумму средств, которую инвестор получит в будущем, а объем финансов, необходимых для инвестирования.

То есть, вычисляя показатель ПС, сначала нужно понять, сколько инвестор хочет заработать от вложений. Затем можно приступать к расчетам при помощи арифметической формулы. Итог анализа – это и есть сумма, которой компания должна располагать на сегодняшний день, чтобы получить задуманный объем дохода.

Формула для вычисления приведенной стоимости

Анализ приведенной стоимости строится на расчете показателя. Его вычисление реализуется при помощи формул. Вид арифметического выражения напрямую зависит от метода начисления процентов: простого или сложного:

• Метод простых процентов предполагает расчет приведенной стоимости в традиционном порядке. Объем ожидаемых доходов дисконтируют в обычном порядке.
• Прием сложных процентов предполагает присоединение суммы процентов прошлого периода к общему объему финансов. Данную операцию в экономической теории называют капитализацией.

В связи с этим, каждый период денежный поток, поддающийся дисконтированию, должен быть разным:

Метод определения приведенной стоимости	Формула	Расшифровка формулы
Простые проценты	БС / (1 + СД)н	БС – будущая стоимость; СД – ставка дисконтирования; Н – число периодов инвестирования
Сложные проценты	БС / (1 + СДп)н*м	БС – будущая стоимость; СДп – ставка дисконтирования за период; Н – число периодов инвестирования; М – число капитализаций в год

Важно! Оценивая результаты расчета приведенной стоимости методом простых и сложных процентов, нужно опираться на наименьший результат. Это означает, что для получения одной и той же суммы дохода компании придется вложить меньше собственных средств.

Кроме ПС, можно определить показатель чистой приведенной стоимости. Вычисления проводятся также при помощи формулы:

(БС / (1 + СД)^н) ^– ПИ,

где БС – будущая стоимость (предполагаемый доход);

СД – ставка дисконтирования (процентная ставка по договору);

Н – число периодов инвестирования;

ПИ – объем первоначальных вложений.

Таким образом, чистая приведенная стоимость  — это ПС за исключением суммы инвестирования в проект.

Пошаговый алгоритм расчета приведенной стоимости

Для расчета ПС рекомендуется использовать пошаговую инструкцию, которая поможет избежать ошибок:

1. Определяем период инвестирования. То есть, промежуток времени, через который инвестор планирует получить определенный доход.
2. Вычисляем объем прибыли от инвестирования при условии соблюдения договора. Обычно показатель берется из документации по планированию.
3. Находим ставку дисконтирования. Она определяется путем деления процентной ставки доходности на 100. В случае применения методики сложных процентов, определяем число случаев капитализации за 1 год.
4. Рассчитываем приведенную стоимость путем замены буквенных выражений формулы на соответствующие числовые значения.

Сам процесс вычисления не сложен. Труднее исключить допущение ошибок, так как будущую доходность принято считать путем сложения денежных потоков.

Пример вычисления приведенной стоимости

Приведем пример вычисления приведенной стоимости на основании следующих условий. Компания планирует получить доход 1 млн. рублей от помещения денежных средств на депозит сроком на 5 лет. Банк предлагает два варианта начисления процентов: сложный (12% годовых) и простой (10% годовых). Перед заключением договора необходимо выбрать оптимальный метод. Для этого рассчитывается приведенная стоимость приемом сложных и простых процентов.

В первую очередь, определим приведенную стоимость методом простых процентов:

1 млн. руб. / (1 + 0,1)⁵ = 951465, 68 руб.

Таким образом, чтобы через 5 лет получить доход в размере 1 млн. рублей под 10% годовых, необходимо вложить 951465, 68 рублей. Теперь найдем приведенную стоимость методом сложных процентов. Допустим, проценты начисляются каждый месяц, пополнений не предусмотрено:

1 млн. руб. / (1 + 0,12 / 12)^{5 * 12} =  550375,73 руб.

Получается, что вложив 550375,73 руб. под сложные проценты 12% годовых, через 5 лет компания сможет иметь доход 1 млн. рублей Таким образом, гораздо выгоднее поместить средства на депозит под сложные проценты, так как при условии получения одинакового дохода за аналогичный промежуток времени необходимо вложить гораздо меньше средств.

Чтобы рассчитать чистую приведенную стоимость, из ожидаемого дохода нужно отнять рассчитанный показатель ПС:

1. ЧПС методом простых процентов: 1 млн. руб. – 951465,68 руб. = 48534,32 рубля;
2. ЧПС методом сложных процентов: 1 млн. руб. – 550375,73 = 449624,27 рублей.

Таки образом, можно сделать вывод о том, что чистая приведенная стоимость методом сложных процентов гораздо выше, чем при альтернативном варианте.

Альтернативные методы расчета приведенной стоимости

Альтернативным методом расчета приведенной стоимости является автоматизированный прием, основанный на использовании специализированных программ. Существует масса сервисов, которые помогают безошибочно рассчитать показатель. Если подобных инструментов нет, можно использовать стандартный Excel.

Excel – это программа, входящая в стандартный пакет Microsoft Office. Сервис наделен множествами функций, которые позволяют безошибочно проводить расчеты в автоматическом режиме по заданным параметрам. Главная сложность использования Excel заключается в неумении пользователей применять встроенные сервисы.

Основным достоинством расчета приведенной стоимости в Excel является то, что программа имеет функцию вычисления данного показателя. Поэтому нет необходимости вводить формулу. Достаточно выбрать инструмент и выделить участвующие в расчете ячейки.

Расчет приведенной стоимости в Excel

Вычисление приведенной стоимости в Excel производится при помощи встроенного инструмента. Нет необходимости вводить сложные формулы. Достаточно выбрать опцию и отразить ячейки, принимающие участие в анализе. Определение ПС в Excel имеет следующий алгоритм:

• создаем таблицу (начиная с 4 и далее строки), состоящую из трех столбцов – период, сумма периода и приведенная стоимость;
• в ячейках первого столбца отражаем последовательность периодов, в ячейках второго – сумму денежных потоков;
• третий столбец посвящен приведенной стоимости по временным промежуткам;
• чуть выше таблицы, например, в первой строке, прописываем значение ставки дисконтирования, во второй – итоговое значение приведенной стоимости, но ячейка, посвященная результату показателя, будет пустой;
• итоговую приведенную стоимость также необходимо отобразить в заключительной ячейке столбца показателя;
• после того, как все данные введены, можно приступать к указанию формул.

Положительной особенностью Excel является тот факт, что программа имеет встроенный инструмент для расчета приведенной стоимости. Достаточно найти функцию и выделить ячейки, необходимые для расчета. Сама формула для вычисления и результат сформируются автоматически.

Важно! Для расчета чистой приведенной стоимости отражение временных промежутков нужно начинать с нулевого года с отрицательным значением суммы инвестиций.

В дальнейшем, автоматически сформированную формулу нужно видоизменить, добавив сумму ячейки первоначальных вложений. Конечный результат ПС должен быть всегда положительным.

Чистая приведенная стоимость проекта

Краткая теория

---

Одним из самых популярных показателей эффективности
инвестиционных проектов долгое время был (в докомпьютерную эпоху) показатель,
который называется NPV − NetPresent Value.
Варианты русских переводов: чистый дисконтированный доход (ЧДД), чистый
приведенный доход (ЧПД), чистая приведенная величина денежных поступлений
(ЧПВД) не очень прижились.

Таким образом, NPV
есть разность современной стоимости всех доходов и современной стоимости всех
затрат по инвестиционному проекту. Напомним, что инвестиционный проект − это
последовательность взаимосвязанных инвестиций, растянутых на несколько
временных периодов, отдача от которых (доходы) тоже растянуты во времени.
Выбирая в качестве нормы доходности (уровня доходности) некоторую ставку
сложных процентов, называемую ставкой дисконирования или сравнения i, находят PV доходов и PV затрат и разность между ними, т. е. чистый приведенный доход,
или NPV.

Если анализируются несколько альтернативных проектов, то более
выгоден с финансовой точки зрения тот, NPV
которого больше. Если величина NPV
рассматриваемого проекта отрицательна (NPV
<0), то доходность этого проекта ниже стоимости капитала при ставке
сравнения i, с помощью которой
проводилось дисконтирование, т. е. на рынке есть более привлекательные варианты
инвестирования, например, помещение этих денег в банк под i% годовых. Если NPV>0,
то доходность проекта больше, чем альтернативный вариант на финансовом рынке со
ставкой i. Очевидно, что из двух
альтернативных инвестиционных проектов с равными инвестиционными затратами
выбирается тот, который обеспечивает наибольшее значение NPV.

Пример решения задачи

---

Задача

Инвестиции в сумме 750 тыс.р.
принесут за первое полугодие 230 тыс.р.
дополнительного дохода, за второе 370 тыс.р. и за
третье 600 тыс.р. Ставка дисконирования равна 23%.
Рассчитайте чистую приведенную стоимость проекта и сравните ее с чистой
приведенной стоимостью того же проекта, но при условии, что доходы поступали бы
равномерно, то есть по 400 тыс.р. в полугодие.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Чистую
текущую стоимость проекта можно найти по формуле:

 -денежный поток проекта в -м периоде,

 -ставка сравнения

Таким образом, чистая приведенная
стоимость проекта с равномерным поступлением доходов больше.

Многие аспекты управления инвестициями часто связаны с активами, которые предполагают серию (т.е. последовательность) денежных потоков, возникающих с течением времени.

Денежные потоки могут быть очень неравномерными, относительно одинаковыми или равными.

Также денежные потоки могут возникать в течение относительно коротких периодов времени, более длительных периодов времени или даже растягиваться на неопределенный срок.

Далее мы обсудим, как найти текущую или приведенную стоимость (PV) серии денежных потоков.

Расчет текущей стоимости (PV) серии равных денежных потоков.

Начнем с обычного или простого аннуитета (англ. ‘ordinary annuity’). Напомним, что обычный аннуитет означает равные аннуитетные платежи, причем 1-й платеж начинается через 1 период (т.е. в конце текущего периода / начале следующего / при (t = 1)).

Всего простой аннуитет включает (N) платежей с первым взносом при (t = 1) и последним при (t = N).

Мы можем выразить текущую (приведенную) стоимость обычного аннуитета как совокупность текущей стоимости каждого отдельного аннуитетного платежа, как указано ниже:

Поскольку аннуитетный платеж (A) является константой в этом уравнении, его можно вывести за скобки. Таким образом, это выражение можно привести к следующей формуле:

( dstl PV = A left [1- dst {1 over (1 + r)^N} over r right] ) (Формула 11)

Точно так же, как и при вычислении будущей стоимости (FV) обычного аннуитета, мы находим приведенную стоимость (PV), умножая сумму аннуитета на фактор текущей стоимости аннуитета (англ. ‘present value annuity factor’) — он заключен в квадратные скобки в Формуле 11.

Пример расчета текущей (приведенной) стоимости обычного аннуитета.

Предположим, вы рассматриваете возможность покупки финансового актива, который обещает выплату в €1,000 каждый год в течение 5 лет с первым платежом через год.

Норма прибыли составляет 12% в год.

Сколько вы должны заплатить за этот актив?

---

Решение:

Чтобы узнать стоимость финансового актива, используйте Формулу (11) приведенной стоимости обычного аннуитета, со следующими данными:

Серия денежных потоков в размере €1,000 в год в течение 5 лет на текущую дату составляет €3,604.78 при дисконтировании по ставке 12%.

---

Необходимость отслеживания фактических календарных сроков приводит нас к специфическому типу аннуитета: авансовому аннуитету или аннуитету пренумерандо (англ. ‘annuity due’).

При авансовом аннуитете 1-ый платеж выполняется в текущую дату ((t) = 0). В общей сложности авансовый аннуитет включает (N) платежей.

На рисунке ниже представлена временная шкала авансового аннуитета из 4-х платежей в размере $100.

Авансовый аннуитет в размере $100 за период.

На рисунке мы можем видеть авансовый аннуитет с 4-мя периодами, состоящий из двух частей:

• единовременная сумма в размере $100 на текущую дату (при (t) = 0) и
• обычный аннуитет в размере $100 за период в течение 3-х периодов.

При ставке дисконтирования в 12% четыре денежных потока в размере 100$ в этом примере авансового аннуитета будут стоить $340,18.

---

Существует альтернативный способ расчета приведенной стоимости авансового аннуитета.

По сравнению с обычным аннуитетом каждый платеж авансового аннуитета дисконтируется на 1 период раньше.

Поэтому мы можем модифицировать Формулу 11, умножив правую часть уравнения на (1 + (r)):

Выражение стоимости будущих денежных потоков в сегодняшнем эквиваленте дает нам удобный способ сравнения аннуитетов. Следующий пример иллюстрирует этот подход.

Пример расчета авансового аннуитета как суммы текущей стоимости единичного денежного потока и обычного аннуитета.

Вы выходите на пенсию сегодня и должны либо получить свое пенсионное пособие в виде паушальной суммы (т.е. единовременной выплаты всех пенсионных накоплений), либо в виде аннуитета.

Сотрудник вашей компании, занимающийся выплатой пособий, предлагает вам две альтернативы:

• немедленную единовременную выплату в размере $2 млн. или
• аннуитет с 20 платежами в размере $200 000 в год с первым платежом от текущей даты.

Процентная ставка в вашем банке составляет 7% годовых с ежегодным начислением процентов.

Какой вариант обеспечивает большую текущую стоимость? (Игнорируйте любые налоговые различия между двумя вариантами.)

Решение:

Чтобы сравнить эти два варианта, необходимо найти текущую стоимость каждого из них в момент времени
(t) = 0 и выбрать наибольшее значение.

Приведенная стоимость первого варианта составляет $2 млн., т.е. первый вариант уже выражен в сегодняшнем эквиваленте.

Второй вариант — аннуитет. Поскольку первый платеж происходит при (t) = 0, вы можете разделить этот аннуитет на две части:

• немедленную выплату $200,000 от текущей даты ((t) = 0) и
• обычный аннуитет в размере $200,000 в год в течение 19 лет.

Чтобы рассчитать этот аннуитет, вам нужно найти приведенную стоимость обычного аннуитета, используя Формулу 11, а затем добавить к нему $200,000.

19 платежей в размере $200 000 имеют текущую (приведенную) стоимость в размере $2,067,119.05. Добавив к этой сумме первоначальный платеж в размере $200,000, мы обнаружим, что общая стоимость аннуитета составляет $2,267,119.05.

Текущая стоимость аннуитета больше, чем единовременная альтернатива в размере $2 млн.

---

Теперь рассмотрим другой пример, подтверждающий эквивалентность текущей и будущей стоимости.

Пример расчета прогнозируемой приведенной стоимости обычного аннуитета.

Менеджер немецкого пенсионного фонда ожидает, что пенсионерам будут выплачиваться пособия в размере €1 млн. в год. Пенсионные выплаты начнут осуществляться через 10 лет от текущей даты, при (t) = 10.

После того, как пособия начнут выплачиваться, эти выплаты продлятся до (t) = 39, что составляет в общей сложности 30 платежей.

Какова текущая (приведенная) стоимость пенсионного обязательства, если соответствующая годовая ставка дисконтирования для обязательств по пенсионной программе составляет 5% годовых, начисляемых ежегодно?

---

Решение:

Эта задача связана с аннуитетом, первый платеж по которому наступает через 10 лет, при (t) = 10.

При этом, на момент (t) = 9 мы имеем обычный аннуитет с 30 платежами. Мы можем вычислить приведенную стоимость (PV) этого аннуитета с помощью Формулы 11, а затем посмотреть на нее на временной шкале.

Приведенная стоимость обычного аннуитета с первым платежом в момент времени t = 10 (в млн. €).

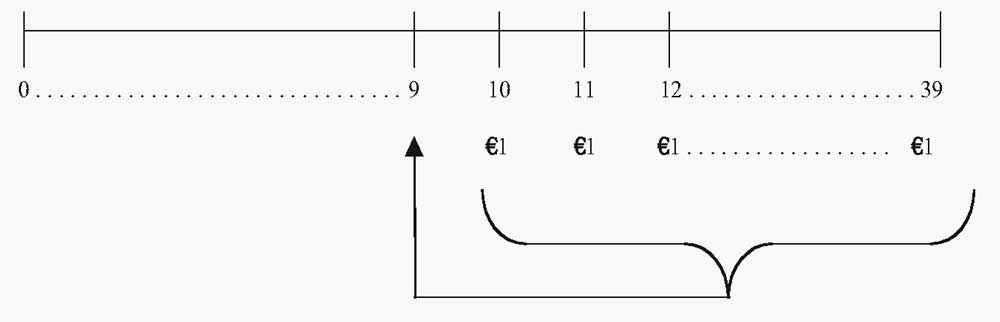
На временной шкале мы отразили пенсионные выплаты в размере €1 млн., занимающие отрезок от (t) = 10 до (t) = 39.

Фигурная скобка и стрелка обозначают процесс нахождения текущей стоимости аннуитета, дисконтированной к моменту времени (t) = 9.

Текущая стоимость (PV) пенсионных выплат по состоянию на (t) = 9 составляет €15,372,451.03.

---

Далее задача заключается в том, чтобы найти приведенную стоимость на текущую дату (при (t) = 0). Теперь мы можем полагаться на эквивалентность текущей стоимости и будущей стоимости

Как показано на временной лини, мы можем рассматривать сумму при (t) = 9 в качестве будущей стоимости с точки зрения (t) = 0.

Мы вычислим приведенную стоимость (PV) при (t) = 0 следующим образом:

Приведенная стоимость на текущую дату (при (t) = 0) пенсионного обязательства составляет €9,909,219.00.

---

Приведенный пример иллюстрирует три процедуры:

• определение текущей (PV) или будущей стоимости (FV) любой последовательности денежных потоков;
• признание эквивалентности текущей и будущей стоимости; а также
• отслеживание фактического календарного времени на временной шкале при вычислениях, связанных с временной стоимостью денег (TVM).

Как вычислять приведенную стоимость (PV) бесконечной серии равных денежных потоков — бессрочный аннуитет?

Рассмотрим случай обычного аннуитета, который длится бесконечно. Такой обычный аннуитет называется бессрочным аннуитетом или перпетуитетом или вечной рентой (англ. ‘perpetuity’ или ‘perpetual annuity’).

Чтобы получить формулу для текущей стоимости перпетуитета, мы можем модифицировать Формулу 10, чтобы учесть бесконечную последовательность денежных потоков:

( dstl PV = A sum _{t = 1} ^{infty} left[ 1 over (1 + r)^t right] ) (Формула 12)

Пока процентные ставки положительны, сумма факторов текущей стоимости позволяет получить формулу в следующем виде:

( dstl PV = A / r ) (Формула 13)

Чтобы понять смысл этого преобразования, обратите внимание на Формулу 11 приведенной стоимости обычного аннуитета.

Поскольку (N) (количество периодов в аннуитете) переходит в бесконечность, выражение ( 1 / (1 + r)^N ) приближается к 0, а Формула 11 упрощается до Формулы 13.

Эта формула потребуется, когда мы будем оценивать дивиденды по акциям, поскольку акции не имеют предопределенного срока действия.

Формула 13 справедлива только для бессрочного аннуитета с равными платежами.

В примере выше первый платеж произошел при (t = 1); поэтому мы вычисляем текущую стоимость при (t = 0).

Некоторые финансовые активы также соответствуют концепции бессрочного аннуитета. Определенные государственные облигации и привилегированные акции являются типичными примерами финансовых активов, которые обеспечивают равные выплаты в течение неопределенного срока.

Пример расчета текущей стоимости (PV) перпетуитета.

Британское правительство когда-то выпускало форму ценных бумаг, называемых «консолями» (англ. ‘consol bond’). Это — бессрочные облигации (англ. ‘perpetual bond’),  которые обеспечивают равные денежные выплаты в течение неограниченного срока.

Если бессрочная облигация приносит £100 в год в течение неограниченного срока, сколько бы она стоила сегодня, если норма прибыли составляет 5%?

---

Решение:

Чтобы ответить на этот вопрос, мы можем использовать Формулу 13 со следующими данными:

Облигация будет стоить £2 000.

Приведенная стоимость на момент времени, отличный от текущей даты (t = 0).

На практике финансовым аналитикам часто приходится находить текущие значения стоимости, на различные моменты времени, отличные от (t = 0).

Если мы рассчитаем перпетуитет, начинающийся с платежа в размере $100 на 2-й год, то мы получим:

( PV_1 = $100 / 0,05 = $2,000 ) при 5%-й ставке

Кроме того, мы можем рассчитать PV на текущую дату как:

( PV_0 = $2,000 / 1.05 = $1,904.76 )

---

Рассмотрим аналогичную ситуацию, в которой денежные потоки в размере $6 в год начинаются в конце 4-го года и продолжаются в конце каждого года после этого с последним потоком денежных средств в конце 10-го года.

По состоянию на конец 3-го года мы сталкиваемся с типичным 7-летним обычным аннуитетом. Мы можем найти текущую стоимость аннуитета на конец 3-го года, а затем привести эту стоимость к текущей дате.

При процентной ставке 5% денежные потоки в размере $6 в год, начинающиеся в конце 4-го года, будут стоить $34,72 на конец 3-го года ((t) = 3) и $29,99 на текущую дату ((t) = 0).

---

Следующий пример иллюстрирует важную концепцию, согласно которой начинающийся в будущем аннуитет или перпетуитет может быть выражен в текущей стоимости за один период до первого платежа. Эта стоимость может быть приведена к текущей стоимости на сегодняшнюю дату.

Пример расчета приведенной стоимости (PV) бессрочного аннуитета (перпетуитета) с отсроченной первой выплатой.

Рассмотрим перпетуитет с равными платежами в £100 в год, с первой выплатой, начинающейся при (t = 5).

Какова будет его текущая (приведенная) стоимость на сегодняшнюю дату (при t = 0), при 5-процентной ставке дисконтирования?

---

Решение:

Во-первых, мы находим приведенную стоимость перпетуитета при (t = 4), а затем дисконтируем эту сумму к текущей дате (t = 0).

Напомним, что у перпетуитета и обычного аннуитета первый платеж осуществляется на конец первого периода, что объясняет индекс (t = 4) для нашего расчета приведенной стоимости).

---

1. Находим текущую стоимость перпетуитета при (t = 4):

---

2. Находим текущую стоимость будущего значения при
(t = 4).

С точки зрения сегодняшней даты (t = 0) текущую стоимость в £2,000 можно считать будущей стоимостью.

Теперь нам нужно найти текущую стоимость £2,000 при
(t = 0):

Приведенная стоимость перпетуитета на текущую дату составляет £1,645.40.

---

Как обсуждалось ранее, аннуитет представляет собой серию платежей с фиксированной (одинаковой) суммой в течение определенного количества периодов.

В ситуации с перпетуитетом число периодов бесконечно. В этом случае мы предоставляем бессрочное обязательство производить платежи, и эти платежи имеют одинаковую сумму. Тем не менее, первая (1) часть перпетуитета отсрочена и выплачивается при (t) = 5; после этого платежи продолжаются бесконечно.

Выплаты по второй (2) части перпетуитета компенсируют смещение 1-го платежа первой (1) части перпетуитета к (t) = 5.

Благодаря этому перпетуитет с отсроченной 1-й выплатой (до (t) = 5) обеспечивает выплаты при (t) = 1, 2, 3 и 4. Выплаты за эти 4 периода точно соответствуют определению обычного аннуитета с четырьмя платежами.

Таким образом, мы можем представить обычный аннуитет как разницу между двумя перпетуитетами с равными платежами, но с разными датами начала выплат.

Следующий пример иллюстрирует этот результат.

Пример расчета приведенной стоимости обычного аннуитета как разницы между текущей стоимостью (PV) и прогнозируемым (отсроченным) перпетуитетом.

С учетом 5%-ой ставки дисконтирования, найдите текущую (приведенную) стоимость 4-летнего обычного аннуитета в размере £100 в год, с выплатами начиная с 1-го года, в качестве разницы между следующими двумя перпетуитетами:

• Перпетуитет 1 на £100 в год, начиная с 1-го года
  (первый платеж при (t) = 1).
• Перпетуитет 2 на £100 в год, начиная с 5-го года
  (первый платеж при (t) = 5).

---

Решение:

Если мы вычтем Перпетуитет 2 из Перпетуитета 1, мы получим обычный аннуитет в размере £100 за 4 года (платежи при (t) = 1, 2, 3, 4).

Вычитая текущую стоимость Перпетуитета 2 из Перпетуитета 1, мы придем к текущей (приведенной) стоимости четырехлетнего обычного аннуитета:

Текущая стоимость 4-летнего обычного аннуитета равна £2,000 — £1,645.40 = £354.60.

Как вычислять приведенную стоимость (PV) для серии неравных денежных потоков?

Когда мы имеем неравные денежные потоки, мы должны сначала найти приведенную стоимость (PV) каждого отдельного денежного потока, а затем суммировать соответствующие значения PV.

Для серии (последовательности) с большим количеством денежных потоков мы обычно используем электронную таблицу.

В таблице ниже приведена последовательность денежных потоков с

• временными периодами в 1-м столбце,
• денежными потоками во 2-м столбце и
• текущей стоимостью (PV) каждого денежного потока в 3-м столбце.

В итоговой строке таблице показана сумма приведенных значений для всей серии денежных потоков.

Серия неравных денежных потоков и их приведенная стоимость при ставке 5%.

Период	Денежный поток ($)	PV при t=0
1	1,000	$1,000(1.05)-1 =	$952.38
2	2,000	$2,000(1.05)-2 =	$1,814.06
3	4,000	$4,000(1.05)-3 =	$3,455.35
4	5,000	$5,000(1.05)-4 =	$4,113.51
5	6,000	$6,000(1.05)-5 =	$4,701.16
		Сумма =	$15,036.46

Мы могли бы рассчитать будущую стоимость (FV) серии этих денежных потоков, вычислив ее по отдельности для каждого потока с использованием формулы расчета будущей стоимости.

Однако мы уже знаем текущую стоимость этой серии, поэтому мы можем легко применить принцип временной эквивалентности для всей суммы денежных потоков сразу.

Будущая стоимость серии денежных потоков составляет $19,190.76 и эквивалентна единовременному денежному потоку размере $15,036.46, с приведением к периоду (t) = 5:

Содержание

Инвестирование позволяет получать стабильный доход. Можно вкладывать деньги в финансовые проекты, в новый бизнес или в расширение уже существующей компании. 

Чтобы не ошибиться с выбором объекта капиталовложения, люди используют инструменты, предназначенные для быстрого определения эффективности инвестиционного проекта. Один из них – расчет NPV.

Что такое NPV

Net Present Value дословно переводится как «чистая приведенная стоимость». Обычно этот показатель используют, чтобы понять, стоит ли вкладывать деньги в проект. Иногда с его помощью рассчитывают финансовые характеристики за определенный период времени.

Например, инвестор хочет вложить 5 миллионов рублей. Его интересуют сроки окупаемости проекта и возможный заработок. Показатель NPV позволит понять, каким будет размер чистой прибыли через год, 5 или 10 лет. От результатов его расчета часто зависит окончательное решение – насколько целесообразно вкладывать деньги в конкретный проект.

Зачем нужно считать NPV

В первую очередь NPV проекта показывает, когда и в каком количестве вернутся вложения и вернутся ли они вообще. Инвесторы часто сравнивают несколько проектов, чтобы определить, какой из них окажется наиболее прибыльным. В этом случае формула тоже работает. 

Существуют 3 цели, для которых используют расчет NPV:

• определение размера первоначальных вложений;
• вычисление сроков окупаемости;
• оценка размеров дохода, необходимого для окупаемости.

Преимущества и недостатки подсчета NPV

Если результат подсчета NPV проекта оказывается положительным, значит, проект экономически эффективен, и потенциальные инвесторы обратят на него больше внимания. При расчете NPV можно учитывать разные сроки, складывать показатели отдельных проектов и принимать во внимание дополнительные риски. Все это – неоспоримые преимущества расчета NPV.

Главные недостатки – сложность и сравнительно низкая точность расчета NPV, а речь идет о размере будущей прибыли. Ее невозможно точно предсказать, так как темпы роста, инфляция и курс валют постоянно меняются. Если учитывать в формуле много дополнительных рисков, сложность подсчета увеличивается и растет вероятность допустить ошибку.

Формула расчета

Стандартная NPV-формула выглядит следующим образом:

n – период расчета;

Pk – денежные потоки за выбранный период времени;

i – ставка дисконтирования;

IC – размер первоначальных вложений.

Важно учесть все составляющие, и здесь многое зависит от конкретного проекта. Вложения нужны для того, чтобы увеличить прибыль, но для небольшого магазина и крупной фабрики эти суммы будут совершенно разными. Определение срока окупаемости тоже зависит от множества факторов. Хотя сложнее всего – рассчитать денежные потоки и ставку дисконтирования.

Денежные потоки

Под денежными потоками понимают все финансовые поступления и расходы. Под поступлениями чаще всего подразумеваются продажи, хотя встречаются и другие их виды – например, проценты от проведенных сделок. Расходы включают в себя выплату заработной платы сотрудникам, коммунальные платежи, закупку сырья, аренду помещений, обустройство рабочих мест, налоги.

Существуют также предположительные потоки, и рассчитать их гораздо сложнее –  например, грядущее повышение арендной ставки или затраты на запуск на рынок нового продукта. В качестве аналитической базы используют экономические показатели, данные мониторинга конкурентов, ожидаемый эффект от рекламы и другие данные.

Чтобы оценить прибыльность рекламных кампаний, подключите сквозную аналитику Calltouch. Сервис посчитает прибыль, продемонстрирует эффективность рекламы и позволит спрогнозировать результативность кампаний.

Ставка дисконтирования

Узнать NPV проекта невозможно без ставки дисконтирования. Далеко не все инвесторы вкладывают собственные средства – иногда выгоднее взять кредит, чем использовать внутренние ресурсы. Или можно продать акции, если потенциальная прибыль у проекта выше, чем их доходность.

Посчитать ставку в случае с кредитом проще. Достаточно ориентироваться на годовой процент. Если же инвестор планирует использовать деньги с продаж акций, придется сравнивать прогнозы по доходам. И все равно это будет только приблизительная информация.

Как рассчитать NPV

Предположим, что в проект инвестировали 1 000 000 рублей. В качестве периода расчета NPV выбрали 1 год. Ставка дисконтирования равна 15%. Обычно ее переводят в коэффициент, то есть, делят на 100. Если размер денежных поступлений составит 900 000 рублей, получится:

900 000 / (1 + 0,15) – 1 000 000= -217 391

Эта сумма и будет чистой стоимостью, приведенной за год. Так как она отрицательная, проект считается убыточным на выбранном периоде. Но это не значит, что вложения не окупятся – просто увеличьте временной отрезок и используйте формулу:

С каждым годом коэффициент дисконтирования уменьшается, поэтому его нужно возводить в степень. Если взять предыдущий пример, за 3 года получится следующий результат:

900 000 / (1 + 0,15) + 900 000 / (1 + 0,15)² + 900 000 / (1 + 0,15)³ – 1 000 000 = 1 054 902

Так как сумма положительная, проект на этом промежутке времени оказывается прибыльным.

Пример расчета в Excel

Чтобы считать было удобнее, лучше составить таблицу в MS Excel. Преимущество этого способа в том, что можно менять различные показатели, не высчитывая их вручную, и сравнивать несколько проектов. Также в MS Excel предусмотрена функция расчета чистой приведенной стоимости – ЧПС.

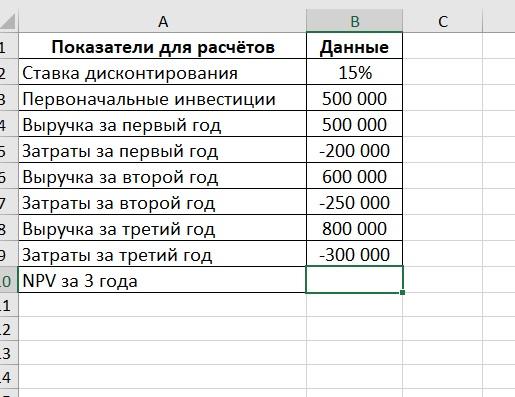
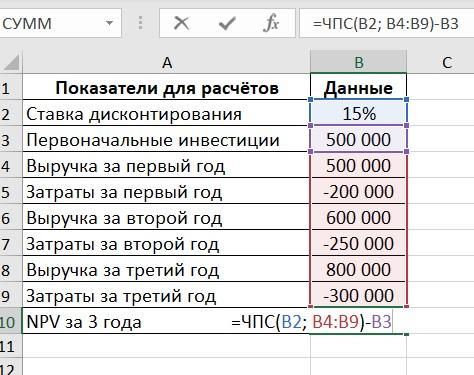
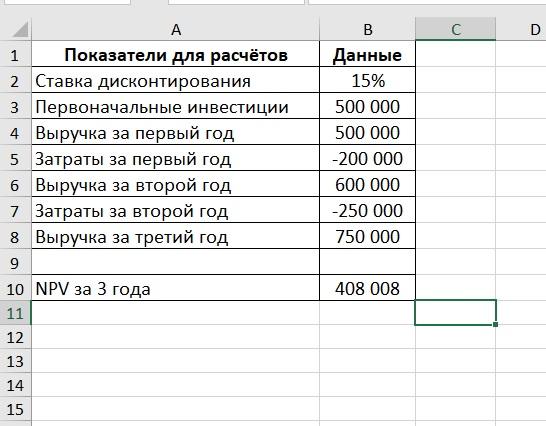
Таблица с показателями выглядит так:

Для расчета в ячейку B10 нужно добавить формулу:

При изменении показателей NPV проекта будет рассчитываться автоматически.

Стоит помнить, что поступления должны быть положительными, а затраты – отрицательными.

Сложности, которые могут возникнуть при расчете

Иногда инвесторы составляют слишком оптимистичный прогноз, но как раз из-за него и возникают трудности с расчетом NPV. Ошибки в вычислении приводят к тому, что инвестиции не приносят ожидаемого дохода.

Здесь можно выделить 4 причины:

1. Ошибка в вычислении ставки дисконтирования. Проценты в банках по текущим кредитам обычно не меняются, а вот рост инфляции и изменения курса акций предугадать невозможно.
2. Отсутствие учета непредвиденных расходов. Например, инвестор вкладывает значительные средства в покупку коммерческой недвижимости и ожидает прибыли от аренды, но не учитывает затраты на ремонт и благоустройство.
3. Искаженное представление о доходах. Ни один бизнес не может гарантировать бесперебойность потока покупателей. Например, в период пандемии многим владельцам бизнеса пришлось приостановить деятельность, а кто-то и вовсе объявил себя банкротом.
4. Нереалистичные и некорректные прогнозы. Любые расчеты следует проверять несколько раз, и в каждом прогнозе инвестор должен быть уверен.

В отличие от суммы инвестиций, рассчитать окупаемость рекламных вложений гораздо проще – для этого существуют специальные сервисы. Чтобы рассчитать доходность рекламы и увеличить прибыльность онлайн-магазина, установите E-commerce Calltouch. На основе результатов отчетов сопоставьте рекламный бюджет и прибыль и скорректируйте рекламную стратегию.

Коротко о главном

• NPV инвестиционного проекта позволяет определить сроки окупаемости и будущую прибыль. 
• Стандартная формула включает в себя размер первоначальных инвестиций, денежные потоки, период и ставку дисконтирования. 
• Для более точного результата лучше учитывать максимум рисков.