Задача как найти уравнение окружности

In geometry, a circle can be defined as the set of all points that are equidistant from a fixed point in the plane, where the fixed point is the center of the circle. The radius is defined as the distance between any point on the circumference of a circle and the center of the circle. The largest chord that passes through the center of the circle; this diameter is referred to as the circle’s diameter. 

Equation of a Circle

A circle can be defined as a closed curve traced out by a point that moves in a plane such that the distance from the given point in that plane is always constant. By using the equation of a circle, we can describe a circle in an algebraic way when the center of the circle and its radius length is known. We require an algebraic equation to represent the circle on a Cartesian plane. So, to find the position of the circle on a Cartesian plane, we require the coordinates of the center and the length of its radius.

The standard form of the equation of a circle

Let’s consider a circle with a center (h, k) and P (x, y) to be any point on the circumference of the circle for finding the standard form of the equation. From the definition of the radius of the circle, 

The radius of the given circle (r) = CP

We can find the value of CP By using the formula for the distance between two points i.e.,

CP = r = √[(x – h)² + (y – k)²]

Now, by squaring on both sides we get,

(x – h)² + (y – k)² = r²

Hence, the standard form of the equation of a circle is,

(x – h)² + (y – k)² = r²

Where (h, k) is the center of the circle and r is the length of the radius.

• Equation of the circle with the center at the origin

Let’s consider that the center of the circle lies at the origin (0, 0) and its radius is “r”. Now, the distance between the origin and any point P (x, y) on the circle is the radius of the circle, i.e.,

OP = r

By using the formula for the distance between two points, 

OP = r = √[(x – 0)² + (y – 0)²]

Now, by squaring on both sides, 

r² = x² + y²

Hence, the equation of the circle with the center at the origin is

x² + y² = r²

• Equation of the circle passing through the origin

Let’s consider that a circle with a center C (h, k) and a radius “r” is passing through the origin. The distance between the center of the circle and the origin is the radius of the circle, i.e.,

OC = r

Draw a line from the center to a point M (h, 0) on the X-axis such that CM is perpendicular to OM.

From the Pythagorean theorem;

OC² = OM² + CM²

r² = h² + k²

Hence, the equation for the circle passing through the origin is,

r² = h² + k²

• Equation of the circle with the center lying on the X-axis

Assume that the center of circle C (h, 0) is on the X-axis and its radius is “r.”

Now, the distance between the center of the circle and any point P (x, y) on the circle is the radius of the circle, i.e.,

CP = r

By using the formula for the distance between two points, we get

CP = r = √[(x – h)² + (y – 0)²]

Now, by squaring on both sides, we get

r² = (x – h)² +y²

Hence, the equation for the circle passing through the origin is,

(x – h)² +y² = r²

• Equation of the circle with the center lying on the Y-axis

Let’s consider that the center of circle C (0, k) lies on the Y-axis and its radius is “r”. Now, the distance between the center of the circle and any point P (x, y) on the circle is the radius of the circle, i.e.,

CP = r

By using the formula for the distance between two points, 

CP = r = √[(x – 0)² + (y – k)²]

Now, by squaring on both sides we get,

r² = x² +(y – k)²

Hence, the equation of the circle with the center lying on the Y-axis is,

x² +(y – k)² = r²

• Equation of the circle touching the X-axis

Let us consider that the center of circle C (h, r) is touching the X-axis and its radius is “r”. Now, the y-coordinate of the center of the circle touching the X-axis is equal to the radius “r”.

Now, the distance between the center of the circle C (h, r) and any point P (x, y) on the circle is the radius of the circle, i.e.,

CP = r 

By using the formula for the distance between two points, we get

CP = r = √[(x – h)² + (y – r)²]

Now, by squaring on both sides we get,

r² = (x – h)² +(y – r)²

Hence, the equation of the circle touching the X-axis is

 (x – h)² +(y – r)² = r²

• Equation of the circle touching the Y-axis

Let’s consider that the center of circle C (r, k) is touching the Y-axis and its radius is “r”. Now, the x-coordinate of the center of the circle touching the Y-axis is equal to the radius “r”. Now, the distance between the center of the circle C (r, k) and any point P (x, y) on the circle is the radius of the circle, i.e.,

CP = r

By using the formula for the distance between two points,

CP = r = √[(x – r)² + (y – k)²]

Now, by squaring on both sides we get,

r² = (x – r)² +(y – k)²

Hence, the equation of the circle touching the Y-axis is

(x – r)² +(y – k)² = r²

• Equation of the circle touching both the X-axis and the Y-axis

Let’s assume that a circle with a center C (r, r) with a radius “r” is touching both the X-axis and the Y-axis. As the circle touches both the X-axis and the Y-axis, the x and y coordinates of the center become equal to the radius of the circle “r”.

Now, the distance between the center of the circle C (r, r) and any point P (x, y) on the circle is the radius of the circle, i.e.,

CP = r

By using the formula for the distance between two points, 

CP = r = √[(x – r)² + (y – r)²]

Now, by squaring on both sides we get

r² = (x – r)² +(y – r)²

Hence, the equation of the circle touching both the X-axis and Y-axis is

(x – r)² +(y – r)² = r²

General Equation of a Circle

The general equation of a circle is given as,

x²+ y² + 2gx + 2fy + c = 0

For all values of g, f, and c.

x² + y² + 2gx + 2fy + c = 0

By adding g² + f² on both sides we get,

x² + y² + 2gx + 2fy + c + g² + f² = g² + f²

Now, by arranging the equation we get

(x² + 2gx + g²) + (y² + 2fy + f²) = g² + f² – c

We know that, (x + g)² =(x² + 2gx + g²) and (y + f)² = (y² + 2fy + f²). So, by substituting these values in the above equation we get

(x + g)² + (y + f)² = g² + f² – c

By comparing the above equation with the standard form of the equation we get

h = -g, k = -f and r² = g² + f² – c 

Where (h, k) are the coordinates of the center of a circle and “r” is its radius.

Hence, the equation x²+ y² + 2gx + 2fy + c = 0 represents a circle having center (-g, -f) and radius r equal to r² = g² + f² – c

• The radius of a circle is real if g² + f² > c.
• The radius of a circle becomes imaginary if g² + f² < c. Hence, the circle will be having a real center and an imaginary radius.

Sample Problems

Problem 1: Find the equation of a circle with the center at the origin and having a radius of 6 units.

Solution:

Given data,

Center of the circle = (0,0) and the radius = 6 units

We know that,

The equation of a circle whose center is at the origin is,

x² + y² = a²

Where a is the radius of the circle.

So, the equation of the circle having a radius of 6 units is,

x² + y² = (6)²

x² + y² = 36

Hence, the equation of the given circle is x² + y² = 36

Problem 2: Find the radius and the center of a circle if the equation of the circle is x² + y² – 8x + 6y + 9 = 0

Solution:

Given data,

The equation of the circle is x² + y² – 8x + 6y + 9 = 0

We can see the  given equation is in the form of  x²+ y² + 2gx + 2fy + c = 0

Now by comparing the both equations,

2g = -8 ⇒ g = -4

2f = 6 ⇒ f = 3

c = 9

Center of the circle = (-g, -f) = (4, -3)

Radius of the circle (a) = √(g² + f² – c)

⇒ a = √[(-4)² + 3² – 9] = √(16 + 9 – 9)

a = √16 = 4 units

Hence, the center of the given circle is (4, -3) and its radius is 4 units.

Problem 3: Find the equation of the circle whose center is (5, 0), and radius is 7 units.

Solution:

Given data,

Center of a circle = (5, 0)

Radius of the circle = 7 units

The general equation of a circle with center (h, k) and radius “a” units is,

(x – h)² + (y – k)² = a²

Now, the equation of the given circle is,

(x – 5)² + (y – 0)² = (7)²

⇒ x² – 10x + 25 + y² = 49

⇒ x² + y² – 10x – 24 = 0

Therefore, the equation of the given circle is x² + y² – 10x – 24 = 0

Problem 4: Find the equation of the circle center passing through the Y-axis whose center is (0,-6) and radius is 10 units. 

Solution:

Given data,

Center of a circle = (0,-6)

The radius of the circle = 10 units.

We know that,

The equation of the circle with the center lying on the Y-axis is,

x² +(y – k)² = r²

x² + (y + 6)² = (10)²

x² + y² + 12y + 36 = 100

x² + y² + 12y – 64 = 0

Hence, the equation of the circle is x² + y² + 12y – 64 = 0

Problem 5: Find the equation of the circle with a radius of 6 inches that touches both the X-axis and the Y-axis.

Solution:

Given data,

The radius of the circle = 6 inches.

As the circle touches both the X-axis and the Y-axis, the x and y coordinates of the center become equal to the radius of the circle “r”.

Hence, the center of the circle = (6,6)

We have,

The equation of the circle touching both the X-axis and Y-axis is

(x – r)² +(y – r)² = r²

(x – 6)² + (y – 6)² = 6²

x² -12x + 36 + y² – 12y + 36 = 36

x² + y² -12x -12y + 36 = 0

Hence, the equation of the circle touching both the X-axis and Y-axis is x² + y² -12x -12y + 36 = 0

Problem 6: Find the equation of the circle with the center at (-7, 4) and the radius of 4 units and touch the X-axis.

Solution:

Given data,

Center of the circle = (-7, 4)

The radius of the circle = 4 units

The equation of the circle touching the X-axis is

(x – h)² +(y – r)² = r²

(x + 7)² + (y – 4)² = 4²

x² + 14x + 49 + y² – 8y + 16 = 16

x² + y² + 14x – 8y + 49 = 0

Hence, the  equation of the circle touching the X-axis is x² + y² + 14x – 8y + 49 = 0

Problem 7: Find the equation of the circle with a radius of 5 units and is touching the Y-axis at the point (0,-3).

Solution:

Given data,

The radius of the circle = 5 units.

The circle is touching the Y-axis at (0,-3)

Now, the x-coordinate of the center of the circle touching the Y-axis is equal to the radius “4 units”.

Hence, the coordinates of the center = (5, -7)

We have,

The equation of the circle touching the Y-axis is

(x – r)² + (y – k)² = r²

(x – 5)² + (y + 3)² = 5²

x² – 10x + 25 + y² + 6y + 9 = 25

x² + y² -10x + 6y + 25 = 0

Hence, the equation of the circle touching the Y-axis is x² + y² -10x + 6y + 25 = 0

Решение задач по теме: «Уравнение окружностей»

Разделы: Математика

За неделю до проведения урока класс делится на четыре группы. Каждая готовит презентацию, отражающую название команды.

1. Образовательные:

систематизация знаний, умений и навыков по теме “Метод координат”,

совершенствование навыков решения задач.

2. Развивающие:

развитие математически грамотной речи,

логического мышления,

культуры диалога.

3. Воспитательные:

воспитывать познавательную активность,

культуру общения,

культуру диалога.

Ход урока

I. Организационный момент.

В начале урока выдается командам оценочный лист ( Приложение 1 ) с целью самостоятельной оценки учащимися степени участия каждого члена команды в подготовке к уроку и его проведении.

Рассказываются правила урока. За каждое правильное решение команде выдается лепесток определенного цвета:

все ответы верные – красный;
одна ошибка – зеленый;
две ошибки – жёлтый.

Лепестки крепятся на магнитную доску, образуя цветок.

Итоговая оценка выставляется с учетом этого бланка, а также учитывается количество и цвет набранных командой лепестков в цветке на доске.

2. Знакомство с командами (представление презентаций, Приложение 2 ).

3. Актуализация знаний учащихся.

– На последних уроках геометрии мы познакомились с еще одним способом решения задач МЕТОДОМ КООРДИНАТ.

Задавая фигуры уравнением и выражая в координатах геометрические соотношения, мы применяем алгебру к геометрии. Так мы поступили, когда выразили через координаты основную геометрическую величину – расстояние между точками, а затем, когда вывели уравнение окружности и прямой.

Пользуясь координатами, можно истолковывать уравнения и неравенства геометрически и таким образом применять геометрию к алгебре и анализу. Графическое изображение функций – первый пример такого применения метода координат

Метод координат в соединении с алгеброй составляет раздел геометрии, называемый “Аналитической геометрией”.

Сегодня я предлагаю еще раз поговорить об уравнении окружности и проследить, как алгебра помогает в решении геометрических задач.

4. Разминка.

– На доске записан ряд уравнений. Какие фигуры они задают?

Команды получают карточки с заданием. Время обдумывания 2мин.

По истечению времени идет опрос команд по очереди.

1	7.
2.	8.
3.	9.
4.	10.
5.	11.
6.	12.

Последнее уравнение вызывает сомнения т.к. ранее не встречалось в таком виде.

Учитель показывает как, выделив полный квадрат, получить уравнение окружности.

Оценить результат работы команд.

Выясните, будет ли данные уравнения задавать окружность, если да, то укажите радиус и координаты центра. Если нет, то почему?

Каждая из команд получают свою карточку. Время 7 минут.

Последние уравнение в каждой карточке не задает окружность, и учащиеся поясняют почему. Оценить ответы.

1. Как могут взаимораспологаться две окружности? Дается время(3 мин.). Предлогается ребятам нарисовать различные варианты на ватмане и показать рисунки. После демонстрации и обсуждения всевозможных вариантов Предлогается следующая задача.

2. Как взаиморасположены линии заданные уравнениями?

и

Изобразите ответ на обратной стороне ватмана (на нем, заранее, нанесена система координат.)

Ответ:

O

Значит: первая внутри второй.

Результат этого задания оценивается следующим образом:

Команда, выполнившая первая – красный; вторая – зеленый; третья – желтый

После подведения итогов предлагается задача общая для всех команд.

Командам выдается карточка с кратким описанием условия. Текст задачи зачитывается.

Окружность задана уравнением .

Точка с координатами (5;4) является центром другой окружности касающейся первой внешним образом. Напишите уравнение этой окружности.

Вопросы для обсуждения:

-Поможет ли рисунок в решении задачи?

-Что можно узнать из уравнения первой окружности?

-Что надо знать, чтобы записать уравнение второй окружности?

-Как можно узнать радиус второй окружности?

Ответ:

Перед следующим заданием полезно повторить:

Какая окружность называется описанной около треугольника?

Что значит, точка принадлежит графику уравнения?

Что необходимо знать для написания уравнения окружности?

Написать уравнение окружности описанной около треугольника с заданными координатами вершин.

Какие, алгебраические, приемы могут быть использованы для решения поставленной задачи? (составление систем уравнений и приемы их решения).

3. С (3;-7)	4. В (1;-4)
Д (8;-2)	К (4;5)
К (6;2)	Д (3;-2)

Следующую задачу решает учитель.

Задача: Что представляет собой множество точек плоскости, отношение расстояний от которых до двух данных точек есть величина постоянная?

Решение: Впервые эту задачу сформулировал и решил Аполлоний Пергский, (260-170 гг. до н.э.)

Решение получилось очень сложное – поскольку применены геометрические приемы. Однако в работах французского математика Рене Декарта эта задача решена более элегантно. Декарт применил метод координат.

Я предлагаю посмотреть на это решение. Итак, пусть даны две точки ,А и В и некоторое положительное число k, равное отношению расстояний до точки М.

1случай. Если k=1,тогда множество точек М есть серединный перпендикуляр к отрезку АВ.

2 случай. Пусть k целое не отрицательное число не равное 1

Для удобства решения возьмем k=2 , т.е. МА: МВ=2.

Введем систему прямоугольных координат. Совместим начало отсчета с точкой В. В качестве положительной полуоси x возьмем луч ВА. (рис.2)

Тогда получим следующие координаты точек: В(0,0), А(a,0), М(x,y). Пусть a=3 опять для простоты рассуждений.

Тогда, пользуясь формулами расстояния между двумя точками, запишем:

Получили уравнение окружности с центром в точке (-1;0) и радиусом r=2.

Значение радиуса не случайно вспомним, что мы выбрали k=2.

Решая задачу в общем виде т.е. при условии ,что точка А имеет координаты (a;0) и k1 получим уравнение окружности в виде

.

Такая окружность называется окружностью Апполония.

Подводится итог урока. Выставляются оценки.

Уравнение окружности.

Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.

В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.

Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.

Геометрическая интерпретация уравнения окружности – это линия окружности.

Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.

Окружность с центром в точке А и радиусом R поместим в координатную плоскость.

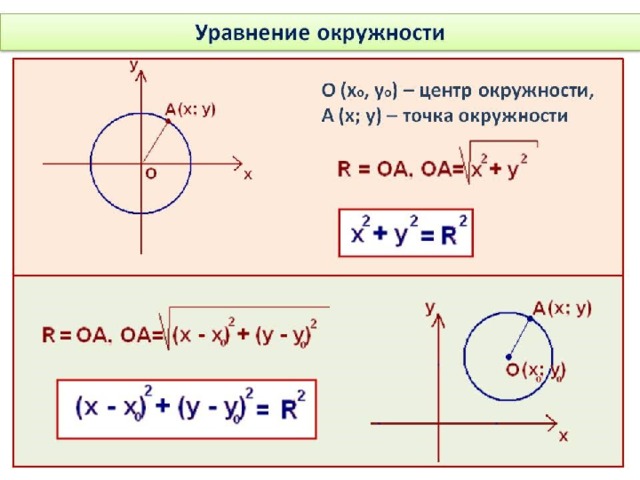
Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:

Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.

Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:

Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.

Решение.
Обратимся к формуле уравнения окружности:
R 2 = (x- a ) 2 + (y- b ) 2

Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3

Получаем:
(x — 2 ) 2 + (y — ( -3 )) 2 = 4 2
или
(x — 2 ) 2 + (y + 3 ) 2 = 16 .

Задача. Принадлежит ли точка уравнению окружности

Проверить, принадлежит ли точка A(2;3) уравнению окружности (x — 2) 2 + (y + 3) 2 = 16.

Решение.
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.

В уравнение ( x — 2) 2 + ( y + 3) 2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3

Проверим истинность полученного равенства
( x — 2) 2 + ( y + 3) 2 = 16
( 2 — 2) 2 + ( 3 + 3) 2 = 16
0 + 36 = 16 равенство неверно

Таким образом, заданная точка не принадлежит заданному уравнению окружности.

9 класс. Геометрия. Метод координат. Уравнение окружности.

9 класс. Геометрия. Метод координат. Уравнение окружности.

• Оглавление
• Занятия
• Обсуждение
• О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Решение задач

Вы­яс­ни­те, какие из дан­ных урав­не­ний яв­ля­ют­ся урав­не­ни­я­ми окруж­но­сти.

Най­ди­те ко­ор­ди­на­ты цен­тра и ра­ди­ус каж­дой окруж­но­сти.

а)

б)

в)

г) ;

д)

Рас­смот­рим каж­дое урав­не­ние в от­дель­но­сти.

а) – окруж­ность,

б) – окруж­ность,

в)
Вы­де­лим пол­ный квад­рат:

урав­не­ние не яв­ля­ет­ся урав­не­ни­ем окруж­но­сти.

г) .
Вы­де­лим пол­ный квад­рат:
– окруж­ность,

д)
Вы­де­лим пол­ный квад­рат:
– окруж­ность,

На окруж­но­сти, за­дан­ной урав­не­ни­ем , най­ди­те точки

а) с абс­цис­сой –4; б) с ор­ди­на­той 3.

Ре­ше­ние: по­стро­им окруж­ность с цен­тром (0;0) ра­ди­у­са 5 (рис. 1).

Рис. 1. Ил­лю­стра­ция к за­да­че

а) Ко­ор­ди­на­ты точек окруж­но­сти с абс­цис­сой –4 яв­ля­ют­ся ре­ше­ни­я­ми си­сте­мы:

По­лу­ча­ем точку и точку

Рис. 2. Ил­лю­стра­ция к за­да­че

б) Ко­ор­ди­на­ты точек окруж­но­сти с ор­ди­на­той 3 яв­ля­ют­ся ре­ше­ни­я­ми си­сте­мы:

Рис. 3. Ил­лю­стра­ция к за­да­че

По­лу­ча­ем точку и ту же самую точку

Ответ: .

За­пи­ши­те урав­не­ние окруж­но­сти ра­ди­у­са r с цен­тром в точке А, если

а)

б)

в)

г)

а) Окруж­ность
Ответ:

б) Окруж­ность .
Ответ:

в) Окруж­ность
Ответ:

г) Окруж­ность
Ответ:

На­пи­ши­те урав­не­ние окруж­но­сти с цен­тром в на­ча­ле ко­ор­ди­нат, про­хо­дя­щей через точку

Рис. 4. Ил­лю­стра­ция к за­да­че

Най­дем ра­ди­ус, как рас­сто­я­ние ОВ:

За­пи­шем урав­не­ние окруж­но­сти с цен­тром О(0;0):

Для кон­тро­ля про­ве­рим, удо­вле­тво­ря­ют ли по­лу­чен­но­му урав­не­нию ко­ор­ди­на­ты точки В:

зна­чит, точка В лежит на окруж­но­сти.

Ответ:

На­пи­ши­те урав­не­ние окруж­но­сти, про­хо­дя­щей через точку А(1;3), если из­вест­но, что центр окруж­но­сти лежит на оси абс­цисс, а ра­ди­ус равен 5.

Сколь­ко су­ще­ству­ет таких окруж­но­стей?

Дано: А(1;3) – точка окруж­но­сти,

Найти: урав­не­ние окруж­но­сти (С; r=5).

Ре­ше­ние: центр ис­ко­мой окруж­но­сти уда­лен от точки А(1;3) на рас­сто­я­ние 5, зна­чит, он лежит на окруж­но­сти с цен­тром в точке А(1;3) ра­ди­у­са 5, но он еще лежит и на оси Ох. По­стро­им окруж­ность (А(1;3); r=5) (рис. 5).

Рис. 5. Ил­лю­стра­ция к за­да­че

Точек, удо­вле­тво­ря­ю­щих нашим усло­ви­ям, на оси Ох две:

Для опре­де­ле­ния ко­ор­ди­нат этих точек со­ста­вим си­сте­му:

За­пи­шем урав­не­ния ис­ко­мых окруж­но­стей:

окруж­ность (

окруж­ность ( и по­стро­им эти окруж­но­сти (рис. 6):

Рис. 6. Ил­лю­стра­ция к за­да­че

Ответ: две окруж­но­сти.

На­пи­ши­те урав­не­ние окруж­но­сти, про­хо­дя­щей через две за­дан­ные точки и В(0;9), если из­вест­но, что центр окруж­но­сти лежит на оси ор­ди­нат.

Дано: окруж­но­сти ;

oкруж­но­сти .

за­пи­сать урав­не­ние окруж­но­сти.

Рис. 7. Ил­лю­стра­ция к за­да­че

За­пи­шем урав­не­ние окруж­но­сти так как окруж­ность про­хо­дит через точки А и В, то их ко­ор­ди­на­ты удо­вле­тво­ря­ют урав­не­нию окруж­но­сти:

Под­ста­вим най­ден­ные зна­че­ния в урав­не­ние.

Ответ:

На­пи­ши­те урав­не­ние окруж­но­сти с цен­тром в точке А(6;0), про­хо­дя­щей через точку В(-3;2).

Дано: А(6;0) – центр,

окруж­но­сти.

Найти: урав­не­ние окруж­но­сти.

Рис. 8. Ил­лю­стра­ция к за­да­че

На­хо­дим ра­ди­ус как рас­сто­я­ние АВ:

За­пи­шем урав­не­ние окруж­но­сти:

Ответ:

Заключение

Итак, мы рас­смот­ре­ли серию задач по теме «Окруж­ность» и в каж­дой за­да­че ис­поль­зо­ва­ли урав­не­ние окруж­но­сти.

На сле­ду­ю­щем уроке мы вы­ве­дем урав­не­ние пря­мой.

Прежде всего,
давайте вспомним, формулу расстояния между двумя точками и еще, повторим, что
уравнение с двумя переменными x и y
называется уравнением линии l, если этому уравнению
удовлетворяют координаты любой точки линии l и не
удовлетворяют координаты никакой точки, не лежащей на этой линии.

Сегодня на уроке мы
попробуем по геометрическим свойствам линии найти ее уравнение.

В качестве линии
рассмотрим окружность радиуса  с
центром в точке .

Пусть центр
окружности имеет координаты . Возьмем на
окружности произвольную точку . Запишем формулу
расстояния между точками C и M.
Мы знаем, что длина отрезка, который соединяет любую точку на окружности с
центром окружности – это радиус. Поэтому можно записать, что MC
равно r. Возведем MC в квадрат
и получим уравнение MC² = r².
Заменим MC² квадрат на выражение  и получим, что если
точка лежит на окружности с радиусом r и центром в
точке C, то координаты этой точки удовлетворяют
уравнению . Если точка не
лежит на окружности, то расстояние от этой точки до центра окружности не равно
радиусу, поэтому координаты таких точек не будут удовлетворять полученному
уравнению. Поэтому можно сказать, что в прямоугольной системе координат уравнение
окружности радиуса r с центром в точке C с координатами  имеет вид: .

Задача. Записать
уравнение окружности с радиусом  и центром в начале
координат.

Решение.

Начало координат
имеет координаты (0;0). Подставим их в уравнение окружности и получим, что
уравнение окружности с радиусом r и
центром в начале координат имеет вид

 

.

Задача. Начертить
окружность, заданную уравнением .

Решение.

Запишем общее
уравнение окружности и проанализируем исходное уравнение. Прежде всего,
определимся с координатами центра окружности. Это будут числа 5 и 3. Теперь
давайте определим величину радиуса окружности.

Поскольку в правой
части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо
извлечь квадратный корень из 4. Получим 2.

 Значит наша
формула задает окружность с центром в точке с координатами пять три и радиусом
равным двум.

Задача. Начертить
окружность, заданную уравнением .

Решение.

Запишем общее
уравнение окружности и проанализируем исходное уравнение. Прежде всего
определимся с координатами центра окружности.

Это будут числа -4
и 2. Теперь давайте определим величину радиуса окружности.

Задача. Начертить
окружность, заданную уравнением .

Решение. Уравнениями
такого типа описываются окружности с центром в начале координат. Теперь давайте
определим величину радиуса окружности. Поскольку в правой части формулы стоит
квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень
из 9.

Значит наша формула
задает окружность с центром в точке с координатами (0;0) и радиусом равным 3.

Теперь давайте
попробуем решить задачу обратную данным.

Задача. Составить
уравнение окружности, которая показана на рисунке.

Как и в предыдущих
задачах мы начнем с определения координат центра окружности. Сделать это
нетрудно. Центр этой окружности совпадает с началом координат, поэтому центр
окружности имеет координаты (0;0).

Нетрудно заметить,
что радиус окружности равен 4.

Запишем уравнение
окружности и подставим найденные значения.

 

 

 

Ответ: .

Решим еще одну
задачу.

Задача. Составить
уравнение окружности, которая показана на рисунке.

Решение.

 – центр окружности

 – радиус окружности

Ответ:.

Задача. Составить
уравнение окружности, которая показана на рисунке.

Решение.

 – центр окружности

 – радиус окружности

 

 

 

Ответ:.

Решая задачи, мы с
вами выполняли один и тоже порядок действий. Давайте еще раз повторим этот
порядок.

Для того, что
бы составить уравнение окружности и построить ее надо:

1. Найти координаты
центра окружности.

2. Найти длину
радиуса этой окружности.

3. Записать уравнение
окружности.

4. Подставить
полученные значения в уравнение окружности.

5. Построить
окружность, если это требуется для решения задачи.

Рассмотрим еще одну
задачу.

Написать уравнение
окружности с диаметром эм эн, если точка эн имеет координаты два три, точка эм
имеет координаты шесть три.

Задача. Написать
уравнение окружности с диаметром , если , .

Решение.

Найдем координаты
центра окружности. Центр окружности является серединой диаметра. Воспользуемся
формулами для нахождения координат середины отрезка.

Получим, что центр
окружности имеет координаты .

Теперь определим
радиус окружности. Для этого найдем расстояние от центра окружности до концов
диаметра.

 

 

Запишем общее
уравнение окружности и подставим в него найденные значения. Тогда получим, что
уравнение данной окружности имеет вид:

Ответ: .

Подведем итоги
урока.

На сегодняшнем
уроке мы познакомились с формулой, которая задает окружность с центром в точке С
(x₀; y₀)
и радиусом r.

Также мы
познакомились с формулой, которая задает окружность с центром в начале
координат и радиусом r.

Мы рассмотрели
задачи на составление уравнения окружности по рисунку и на построение
окружности по заданному уравнению.

Решение задач

по теме

«УРАВНЕНИЕ ОКРУЖНОСТИ»

Геометрия – 9 класс

Задание № 1

Определите по уравнению окружности координаты ее центра и радиус :

А) (Х+2)² + ( У – 5)² = 49

Ответ : О (-2; 5); R= 7

Б) (Х+7)² + ( У + 1)² = 36

Ответ : О (-7; -1); R= 6

В) (Х- 6)² + ( У + 15)² = 81

Ответ : О (6; -15); R= 9

Г) Х ² + ( У -9)² = 2

Ответ : О (0; 9); R= V͞2

Задание № 2

Составьте уравнение окружности, если известны координаты ее центра М и радиус R :

А) М ( 1; -4) , R = 2;

Б) М ( 0; -5) , R = 3;

В) М ( 1; -1) , R = ; = V͞11

Г) М ( 0; 0) , R = 8;

Задание № 2 ( проверка)

А) ) (Х-1)² + ( У + 4)² = 4

Б) ) Х² + ( У –+5)² = 81

В) ) (Х-1)² + ( У + 1)² = 11

Г) ) Х² + У ² = 64

Задание № 3

Составьте уравнение окружности с центром в точке М (1; -4), проходящей через точку А(0; 3).

Задание № 4

Составьте уравнение окружности, диаметром которой является отрезок АВ,

если А( -4; 7), В ( 2; 5 )

Задание № 5

Составьте уравнение окружности, радиусом которой является отрезок КР,

если К (-2; 3), Р ( 5; — 23)

Задание № 6

Составьте уравнение окружности с центром в точке

А(-4; 2), которая касается оси ординат.

Задание № 7

Составьте уравнение окружности, проходящей через точку А( 1; -5 ), центр которой принадлежит оси абсцисс, а радиус равен 13.

Задание № 8

Докажите, что данное уравнение является уравнением окружности, и укажите координаты центра и радиус этой окружности:

А) Х² + У² + 6х – 14у – 5 = 0;

Б) Х² + У² + х = 0

Задание № 9

Найдите координаты центра и радиус окружности ,заданной уравнением

Х² + У² — 18х +2у + 50 = 0. Определите положение точек

А(5; -1), В(2; 4) и С( 13; — 5 ) относительно этой окружности.

С П А С И Б О

З А

Р А Б О Т У !