1. Эвристическая технология в математическом развитиии дошкольников
2. Эвристика («Я нашел!») – направленность деятельности ребенка, ориентированная на создание им нового личностно значимого
продукта.
Эвристическое обучение ориентирует детей на
достижение неизвестного им ранее результата.
Его цель – создание детьми личного
математического опыта и математического продукта.
Основа эвристического обучения –
эвристическая образовательная
ситуация, возникающая
спонтанно или организуемая
педагогом. Это ситуация
актуализации незнания.
Получаемая в ходе решения
ситуации информация всегда
востребована ребенком.
3. Методы эвристики
1. Когнитивные методы:
• Вживание (эмпатия) – «вселение» ребенка в
состояние изучаемого математического объекта,
«очеловечивание» объекта, изучение его изнутри.
Основа – словесные рекомендации педагога:
— Представь, что ты – число 5 (условная мерка,
треугольник, часть суток, день недели и т.п.). Какой
ты? Для чего существуешь? С кем дружишь? Как
выглядишь? Из чего состоишь? Что делаешь?
4.
Образное видение – эмоционально-образное
исследование математического объекта
Предлагается, например, глядя на квадрат,
нарисовать (слепить, собрать из конструктора,
назвать) на что он похож.
• Символическое видение – построение или поиск
ребенком связи между математическим объектом и
символом.
Ребенку предлагают понаблюдать
за объектом (рассмотреть) с целью
изображения его признаков,
свойств символами в графической
или знаковой форме.
5.
• Эвристические вопросы – для поиска сведений
об изучаемом математическом объекте задаются
вопросы (в разном сочетании): Кто? Что? Зачем?
Где? Чем? Как? Когда?
• Конструирование понятий и правил –
после изучения той или иной темы педагог
с помощью сопоставления и обсуждения
помогает детям сформулировать понятия
и правила (счета, измерения, анализа
геометрической фигуры и пр.)
6. Задания когнитивного типа
• Сформулировать правила работы с изучаемым объектом
(измерения, счета, деления на части …)
• Доказать или опровергнуть существование объекта (числа,
геометрической фигуры, дня недели, меры…)
• Найти общие и различные элементы (в написании цифр,
геометрических фигурах, рядах (числовых, геометрических)
• Исследовать объект: его происхождение, смысл, строение,
признаки, функции, связи.
• Эксперимент (мысленный или реальный)
Мысленные эксперименты
— Что можно сделать из прямоугольного листа бумаги?
— На какие фигуры можно разделить квадрат?,
— Какую тень отбрасывает: шар, куб, цилиндр?.
— Закончить рассказ: «Охотник переправляется через
реку. Он нашел: сетку, бревно, подушку, лист бумаги. Он
переправился…
7. Методы эвристики
2. Креативные методы:
Метод придумывания – создание нового объекта
с помощью приемов умственного моделирования:
Замещение (дополнение) качеств одного объекта
качествами другого с целью создания и описания свойств
нового объекта: в загадку (пословицу, стихотворение)
вводятся числа и изменяется вопрос – получается…;
элементы цифры 3 заменяются другими или дополняются и
получаются цифры…; изменяется величина элементов и…
—
Отыскание свойств объекта в других объектах: на что
похожа…
8.
Метод «Если бы…» — детям дается утверждение,
меняющее привычную картину мира, и
предлагается описать результаты такого
изменения: «Если бы все колеса стали
квадратными»; «Если бы люди уменьшились в
несколько раз»; «Если бы пропали все цифры»…
9.
• Метод синектики – мозговой штурм с
использованием аналогий. Предполагает этапы:
— Формулировка проблемы педагогом.
— Формулировка проблемы детьми.
— Генерация идей на основе контрольных вопросов,
наводящих на выяснение сущности проблемы и
трех типов аналогий – прямой, личной,
символической.
Например:
— Педагог предлагает придумать правила
сравнения двух чисел.
— Дети трактуют ее: почему 5 больше 4?
— Контрольный вопрос: зачем нам знать состав числа из
единиц, порядок чисел в числовом ряду, уметь считать,
складывать и вычитать?
— Прямая аналогия: предлагается сравнить 2 конкретных
числа и все действия детей оформляются в правила.
— Личная аналогия: предлагается вспомнить, как конкретные
дети сравнивали числа и на основе этого сформулировать
правила.
— Символическая аналогия: модель, схема сравнения.
10. Задания креативного типа
• Предложить детям придумать: обозначение числа,
дня недели, месяца, математического понятия;
модель.
• Составить задачу, кроссворд, игру (вариант игры),
задание для других детей, математическую сказку
(про число, время, геометрическую фигуру).
• Нарисовать музыку (сказку) с помощью
геометрических фигур.
11. Методы эвристики
—
3. Оргдеятельностные методы:
Детское целеполагание – выбор детьми целей
из предложенных педагогом, их детализация,
конкретизация, обсуждение.
Рецензии – критическая оценка математического
продукта (ответ сверстника, результаты задания)
по следующему алгоритму:
Что понравилось (правильно выполнено).
Как построен рассказ (выполнялось задание).
Какие замечены ошибки, неточности.
Есть ли возражения (исправления).
Есть ли дополнения.
Общая оценка выступления (результата).
12.
• Детское планирование – выделение ребенком с
помощью педагога последовательности
выполнения задания и способов его выполнения
за определенное время. В конце работы
осуществляется анализ реализации плана (по
вопросам воспитателя).
• Рефлексия – организация осознания детьми
своей деятельности. Выделяют 2 вида:
— Текущая рефлексия: анализ своей деятельности
в процессе выполнения задания. Воспитатель по
ходу работы задает вопросы о том что, как и
почему делает ребенок.
— Итоговая рефлексия : оценка ребенком хода и
результатов выполнения задания (с помощью
вопросов воспитателя)
13. Задания оргдеятельностного типа
• Определить цели своей работы на определенные
период (в рамках задания).
• Разработать план выполнения задания.
• Проанализировать свою работу или работу (ответ
сверстника).
14. Эвристические образовательные ситуации
• «Оживить» каждую цифру: нарисовать, слепить,
выложить, вырезать, изобразить телом.
• Придумать и обосновать собственные
изображения чисел.
• Нарисовать города с жителями – сказочными
числами, которые выполняют действия сложения и
вычитания, собираются в таблицы, прячутся в
окружающих предметах.
• Нарисовать (слепить, смоделировать из
конструктора) геометрический сад.
• Подобрать цвета к числам, дням
недели, месяцам.
• Игра-соревнование «Поиск клада»:
дети делятся на группы, каждая из
которых рисует клад и план его
поиска; кто быстрее найдет клад,
тот — победитель.
15.
• Дать свое определение понятиям точка, линия,
треугольник, круг, овал, квадрат, прямоугольник и
др.
• Придумать свои игры с числами и фигурами,
кроссворды, задания.
• Провести математическое исследование
(эксперимент) на выяснение структуры, свойств и
связей чисел, геометрических фигур, величин,
временных и пространственных объектов.
16. Технология проблемного обучения математике
17.
• Проблема – вопрос или комплекс вопросов,
возникающих у ребенка в ходе познания.
• Проблемная ситуация (задача) – теоретическая
или практическая ситуация, в которой нет готового,
соответствующего обстоятельствам решения.
Чтобы устранить проблему, требуются умственные
или практические действия, направленные на
исследование того, что связано с данной
проблемной ситуацией.
В проблемные ситуации (задачи)
включаются проблемные вопросы
(Как разделить квадрат на
треугольники?), занимательные
задачи (Удалить из середины,
лежащих на столе карандашей,
самый длинный, не трогая его)
18. Виды постановки проблем
Проблемная ситуация: для
решения проблемы ребенок
активно действует с
материалом и в результате
получает знание.
Проблемная задача: для
решения проблемы ребенок
рассуждает, анализирует,
получает знание, а затем
проверяет правильность этого
знания в процессе
деятельности.
19. Комплекс упражнений на развитие умения видеть и анализировать проблемы
«Продолжи рассказ»:Володя строит мост.
Вначале он взял два больших кубика и…
Дети продолжают рассказ о процессе построения моста из
деталей конструктора (геометрических форм) Для этого
необходимо проанализировать ситуацию (проблему): уже
выполненные действия соотнести с теми, которые еще
предстоит выполнить; выбранные формы дополнить
формами до целостной конструкции.
«Продолжи арифметическую задачу»
20.
• «Сколько значений у предмета»
Детям предлагается хорошо знакомый предмет: кирпич,
геометрическая фигура, книга, кусок мела, карандаш, мяч…
Задание: найди как можно больше вариантов
использования этого предмета.
Поощряется оригинальность ответов и их количество.
Можно ограничить поиск способов определенной
областью: математикой, конструированием, игрой.
• Наблюдение, как способ выявления проблем.
Ребенок анализирует действительность по заранее
заданной проблеме. Предлагаются проблемы разной
степени сложности: «Почему днем светло?»; «Почему дома
на улице пронумерованы?»; «Почему колеса круглые?»
• Выдвижение гипотезы. Гипотеза – предположение,
суждение о связях и закономерностях объектов и явлений.
Основа выдвижения гипотезы – анализ проблемы:
— При каких условиях этот предмет будет полезным
(бесполезным)?
— Найди причину: мяч не катится, задачу нельзя решить …
21. Одним из условий организации математической подготовки является постановка и решение развивающих задач – развивающее обучение
Развитие мышления, памяти,
внимания, восприятия, творческого
воображения
22. Развитие познавательных процессов.
• Развитие познавательной сферы
осуществляется в дошкольном, младшем
школьном и подростковом (частично) возрастах.
• Развитие данной сферы базируется на принципе
учета возрастных и индивидуальных
особенностей:
• ранний возраст – восприятие;
• дошкольник – память;
• мл.школьник и подросток – мышление.
Обязательной линией развития в любом
возрасте является произвольность
(внимание).
23. Развитие мышления — процесса сознательного отражения действительности в представлениях и суждениях.
В процессе формирования
математических представлений у
детей к старшему дошкольному
возрасту развиваются все виды
мышления:
наглядно-действенное;
наглядно-образное;
словесно-логическое.
24. Направления:
1. Формирование основных компонентов мыслительных операций (анализ, синтез и т.д.)
в разных видах мышления.
2. Становление внутреннего плана действий и
развитие мыслительной рефлексии.
3. Развитие определенного вида мышления:
наглядно-действенного, наглядно-образного,
словесно-логического.
25. Развитие основных компонентов мышления
Мыслительные
операции
Конструктивный
анализ
(разложение
целого на части)
Конструктивный
синтез (познание
целого в
единстве его
частей)
Примеры заданий
-Из каких фигур состоит машина?
-Из каких двух чисел можно
составить число 5?
— На какие две фигуры можно
разделить квадрат?
— Составь дом из геометрических
фигур.
— Составь из двух квадратов
прямоугольник.
— Можно ли составить целый круг
из трех четвертин?
26. Развитие основных компонентов мышления
Мыслительные
операции
Примеры заданий
аналитикосинтетическая
деятельность качественные
анализ (выделение
свойств объекта и
выделение объекта
из группы по
определенному
признаку) и синтез
(объединение
элементов в группу
или выделение
группы на основе
общих признаков)
1. Выбор предмета из группы
по одному признаку:
— Возьми красный круг
— Возьми красный, но не круг
— Возьми круг, но не красный
2. Выбор нескольких предметов
из группы по одному
признаку:
— Выбери все многоугольники
— Выбери все не многоугольники
3. Выбор одного или
нескольких предметов по
нескольким признакам:
— Выбери большой красный
круг (синие треугольники)
27. Развитие основных компонентов мышления
Мыслительные
операции
Сравнение
(сопоставление установление
сходства и
различия между
признаками
объекта,
явления, группы)
Конкретизация
(уточнение)
Примеры заданий
— Чем похожи эти предметы?
(формой) Чем отличаются эти
предметы? (размером)
— Чем похожи полоски? (равные по
длине) Чем отличаются? (разной
ширины и цвета)
— Чем похожи числа 12 и 13? (по 1
десятку) Чем отличаются? (разное
количество единиц)
— Что ты знаешь о треугольнике?
-Как ты решил задачу?
-Что ты знаешь о числе 8?
28. Развитие основных компонентов мышления
Мыслительные
операции
Обобщение
(оформление в
словесной форме
результатов
сравнения)
Систематизация
(расположение в
определенном
порядке)
Классификация
(распределение
объектов в группы
по общим
признакам)
Примеры заданий
-Как можно одним словом
назвать квадрат, прямоугольник
и ромб?
-Как называются числа, в
которых есть десяток и
единицы?
-Разложи полоски от самой
короткой до самой длинной по
порядку.
— Разложи фигуры на группы.
По какому признаку ты это
сделал?
29. Игры и упражнения на развитие компонентов мышления
30. Нахождение предметов, объединенных общим признаком (обобщение и классификация) + формирование понятия множества и счет:
31. Задания на нахождение закономерностей (систематизация) + порядковый счет:
32. «Сложи узор» (кубики Никитина)
Цель: развитие конструктивного анализа и
синтеза.
Задание. Ребенку предлагаются поочередно
картинки с нарисованным на них узором. Он
должен из кубиков выложить такой же узор.
33. «Найди лишнее слово» Цель: развитие мыслительных процессов обобщения, выделения существенных признаков + актуализация
математических
терминов.
Задание: Ребенку читают четыре слова. Три слова
объединены по общему для них признаку, а одно
отличается от них и должно быть исключено.
Варианты серий:
1)квадрат, треугольник, круг, прямоугольник;
2)два, пять, тринадцать, восемь;
3)справа, слева, шесть, впереди;
4)девять, овал, пять, восемь.
34. Упражнения на развитие операции систематизации
• Разложите перед ребенком картинки (предметы) в
произвольном порядке и попросите его определить
порядок размещения картинок (предметов).
35.
36. 2. Становление внутреннего плана действий и развитие мыслительной рефлексии
• Техники:
а) сопоставление данного объекта с другими;
б) отыскивание причин явлений;
в) заканчивание слов, фраз, рассказов;
г) выдвижение гипотез
д) умозаключения и др.
37. «Подбор слов»
Предложите ребенку называть как можно больше
слов, обозначающих какое-либо понятие.
1. Назови слова, обозначающие:
• Геометрические фигуры
• Числа
• Многоугольники
• Множество
2. Назови слова, относящиеся:
• к математике.
• к измерению
• к счету
• к решению задач
• к делению на части
38. «На что это похоже»
Цель: развитие рефлексии
Вариант 1: Детям предлагают рассмотреть
изображения двух яблок: маленького желтого и
большого красного и подобрать среди
геометрических фигур (синего треугольника,
красного квадрата, большого желтого круга,
маленького зеленого круга, красного
треугольника, желтого квадрата) фигуры похожие
сначала на одно, затем на второе яблоко.
Вариант 2: Выбрать фигуры, похожие на оба
яблока.
39. Основа развития мышления старшего дошкольника — развитие логики
Виды логических задач и заданий:
Классификация – объединение объектов и явлений
на основе их сходства:
• по форме,
• цвету,
• размеру,
• назначению (посуда, обувь, игрушки),
• понятийному признаку (многоугольники, числа …)
По степени сложности процедуры:
• по 1 признаку (все квадратные);
• по 2- 3 признакам (синие большие треугольники);
• на основе отсутствия (исключения) признака (не
красные, не круглые);
• по представлению (без наглядности)
40.
Сериация — составление сериационных рядов по
признакам:
цвета (от самого бледного до самого яркого);
размера (от самого узкого до самого широкого);
формы (от самого многоугольного до самого…);
фактуры (от самого шершавого до самого
гладкого);
количества (от карточки с наименьшим
количеством кругов до карточки с наибольшим
количеством).
По степени сложности процедуры:
по одному признаку;
по 2 признакам;
по трем признакам и т.д.
41.
Выводы и умозаключения
1. На основе классификации, сериации,
моделирования
Если Света выше Любы, а Люба выше Наташи, то, что
можно сказать про Свету и Наташу?
Можно ли положить в группу красных многоугольников
красный круг, синий квадрат, красный треугольник?
Почему?
Можно ли составить целый круг из трех половин?
2. На основе системы рассуждений:
от причины к следствию: «Посмотрите, пошел снег, он
падает на дома, деревья, землю. Что изменится?»,
«Наступила осень, поэтому…»
от следствия к причине: «Посмотрите, все кругом
белое. Как вы думаете что случилось ночью?», «Птицы
вьют гнезда потому что…»
42.
Ассоциации:
Отталкиваясь от исходного слова (образа), дети
с помощью педагога составляют цепочку слов
(картинок). Каждая новая ассоциация подбирается
к последнему слову (образу).
Например: К картинке с изображением детей подбираются
другие карточки, которые вставляются в окошки «поезда»:
дети — что подходит: цыплята или медведь?
цыплята — что подходит: галоши или солнце?
солнце — что подходит: блин или чемодан?
блин — что подходит: хлеб или песок?
хлеб — что подходит: плита или кровать?
Детей просят посмотреть на «пассажиров» паровоза и
запомнить их. После этого педагог заменяет какую-нибудь
из карточек на символ и просит угадать, что спряталось
в этом вагончике.
43. Примеры игр и заданий на развитие наглядного и логического мышления
«Раздели на группы»
Цель: развитие образно-логического мышления
– операций анализа и классификации .
Вариант 1. Показать ребёнку картинку, на
которой нарисованы геометрические фигуры,
попросить его разделить фигуры на как можно
большее количество групп. В каждую группу
могут входить фигуры, выделяемые по одному
общему признаку. Ребёнок называет все фигуры,
входящие в каждую группу, и признак, по
которому они выделены.
• Вариант 2. Задание то же, но некоторые фигуры
раскрасить в какой-нибудь цвет.
• Вариант 3. К раскрашенным и белым фигурам
добавить заштрихованные фигуры.
44. Примеры игр и заданий на развитие наглядного и логического мышления
«Подбери число»
• Цель: развитие логических операций анализа,
классификации и сравнения
• Вариант 1. Детям предлагают рассмотреть
набор геометрических фигур, отобрать из них
группу фигур по заданному признаку (все желтые,
все треугольники) и подобрать число (цифровую
карточку) к этой группе, объяснив свой подбор.
• Вариант 2. Подбор группы к числу (цифровой
карточке)
45. Развитие памяти – запечатления, сохранения и воспроизведения ребенком того, что было в его опыте
Память включает в себя:
• запоминание («Запомни — это
квадрат»),
• припоминание («Как называется
эта фигура?»),
• воспроизведение («Покажи
(нарисуй) квадрат!»),
• узнавание («Найди и назови
знакомые фигуры!»).
46. Развивающие математические занятия включают в себя упражнения:
1.
1.
На развитие памяти
зрительной,
слуховой,
двигательной;
На выработку способов
запоминания (произвольность
памяти)
47. Игры на развитие зрительной памяти
«Запомни рисунок»
• Вариант 1. Детям на 30 сек. показывают рисунок
с 3 – 9 разными не цветными фигурами, просят
внимательно рассмотреть и запомнить.
Далее детям показывают другой рисунок, где
есть все фигуры из первого рисунка и ещё 3 – 6
других, и просят его показать все фигуры из 1рисунка.
Вариант 2. Задание то же, но фигуры на рисунках
можно сделать цветными.
Вариант 3. Во втором рисунке некоторые фигуры из
первого рисунка раскрашены в другие цвета.
Необходимо найти фигуру, раскрашенную как на
первом рисунке.
48. Игры на развитие зрительной памяти
«Построй такую же фигуру»
Вариант 1. Разложить перед детьми фигуру из
палочек (домик, квадрат треугольник и т.д.).
Детей просят внимательно посмотреть на эту
фигуру в течение 2 секунд, затем фигуру
закрывают и просят её повторить.
Вариант 2. Фигура складывается из палочек
разного цвета. Ребёнок должен запомнить
расположение палочек по цвету и затем сложить
фигуру.
Вариант 3. Ребенка просят сосчитать палочки, из
которых сделана фигура, и затем сложить фигуру
из такого же количества палочек.
49. Игры на развитие зрительной памяти
«Цифровая лесенка»
• Цель: развитие памяти на цифры.
Вариант 1. Ребенку показывают цифровой ряд,
написанный на карточке, и просят его повторить в
той же последовательности эти цифры, затем
увеличивать этот ряд на одну цифру. Отметить,
какое максимальное количество цифр может
повторить ребенок.
Вариант 2. Задание то же, но цифры
зачитываются без показа. Идет развитие
слуховой памяти.
12358794
50. Рисование по памяти + ориентировка в пространстве и счет Ребенку предъявляется на 1 минуту несложная картинка, затем ее
убирают, и ребенок должен
нарисовать дорисовать по памяти недостающие
детали.
51.
52.
53. Вариант: «заполни шкаф»
54. Игры на развитие слуховой памяти
«Цепочка слов».
• Цель: развитие слуховой памяти на
математические термины
Вариант 1. Детям предлагается запомнить знаки,
слова, которые воспитатель называет.
• Круг, треугольник, квадрат.
• Пятый, шестой, седьмой.
• Вверху, внизу, между.
• Больше, меньше, столько же.
• Минус, плюс, равно.
Затем читается одно из слов тройки, а дети
воспроизводят второе, третье. При анализе
отметить особенность: слова связаны по смыслу
и запоминаются легко. А если нет связи?
Вариант 2. Дети должны воспроизвести все слова
по порядку.
55. Игры на развитие слуховой памяти
«Повтори-ка»
Воспитатель называет слово (число,
геометрическая фигура), ребенок
повторяет его и добавляет свое.
Следующий ребенок перечисляет
ранее названные слова и добавляет
своё слово и т.д. Список слов растет,
запомнить его все труднее.
Побеждает тот, у кого лучше память.
56. Развитие двигательной памяти + ориентировка в пространстве и счет: повторить движения, (дотронуться левой рукой правого уха,
улыбнуться,
присесть…) Или скопировать положение пальцев:
57. Развитие произвольного внимания – избирательного отношения к объектам математической деятельности
Компоненты произвольного
внимания:
Концентрация
Переключение
Объем
Распределение
Устойчивость
58. 1 тип упражнений — на установление сходства и различий (концентрация внимания)
«Фигура»
• Цель: развитие концентрации внимания:
уметь сосредочиться на зрительной
информации; находить отличительные
признаки похожих предметов.
• Дидактический материал: 3 — 10 похожих
геометрических фигур.
• Задание: Вот фигура (у каждого своя).
Внимательно рассмотрите и запомните ее
цвет, количество углов, размер…
• На изучение детям дается 3 мин. После этого
фигуры перемешиваются. Затем каждый
ребенок ищет свою фигуру.
59. «Найди все отличия» (в сочетании со счетом и определением формы):
60. «Найди все отличия» (в сочетании со счетом и определением пространственного расположения)
61. Поиск парных изображений (+ счет, цифры и пространственное расположение)
62.
63. 2 тип упражнений — на определение изменений (концентрация и устойчивость внимания).Объекты заменили, поменяли местами — что
изменилось?
(+ счет, пространственное расположение,
составление и решение задач).
64. 3 тип упражнений – нахождение «спрятанных» объектов: концентрация и устойчивость внимания (+ счет, пространственные
ориентировки, составление
задач, геометрические представления)
65. 4 тип упражнений – лабиринты (устойчивость внимания): Дети должны следить глазами (+ ориентировка в пространстве)
66. 5 тип упражнений — развитие концентрации, объема, устойчивости и избирательности внимания (распределение и переключение) +
закрепление представлений о цифрах,
числах, геометрических фигурах
Упражнение 1
«Зачеркни (раскрась)
цифру(ы)»
Задания:
• Найдите цифру … и
зачеркни (раскрась ее.
• Найдите и зачеркните
(раскрасьте) все цифры
67. Упражнение 2 «Корректурные пробы»
• Материал:
бланк с
заданием.
• Задание:
предлагается
расставить
значки, как в
образце.
68. 3. Словесные и слуховые игры
«Хлопни в ладоши» Называются различные
слова: стол, квадрат, чашка, карандаш,
шесть, книга, воробей, овал и т.д.
Ребенок должен хлопать в ладоши тогда,
когда встретится слово, обозначающее,
например, геометрическую фигуру (число).
Если ребенок сбивается, повторить задание.
• Во второй серии ребенок должен вставать
каждый раз, когда услышит слово,
обозначающее число (фигуру).
• В третьей серии можно объединить первое
и второе задания, т.е. ребенок хлопает в
ладоши при слове, обозначающем число, и
встает при слове, обозначающем
геометрическую фигуру.
69. 6 тип упражнений «Диктанты» — формируются все компоненты внимания.
Ребенку дают лист бумаги, цветные карандаши
и просят его нарисовать в ряд 5-10
треугольников (квадратов, овалов …). Затем
ребенка предупреждают, что задание
произносится только один раз: «Будь
внимательным, заштрихуй красным (синим)
карандашом третий, седьмой и девятый
треугольники». Если ребёнок спрашивает, что
делать дальше, — ответить, чтобы он делал так,
как понял.
Цвет и порядок штриховки варьируется.
70. 7 тип – упражнения с числовыми карточками (объем внимания)
Ребенка просят
посмотреть на
квадрат (остальные
закрываются) и
так же расставить
точки в пустом
квадрате. Время
показа карточки
1-2 секунды, на
воспроизведение
точек отводится не
более 15 секунд
Затем дается
следующая
карточка.
71. 8 тип методик: на развитие концентрированности и переключаемости внимания.
«Я знаю»
• Детям предлагается создание цепочки:
Воспитатель начинает, обращаясь к каждому
ребенку по порядку, называя числительное,
а дети дополняют его названием и
перечислением объектов: «Ты знаешь: 4
времени года, 5 пальцев на руке, 6 героев
сказки «Репка», 7 дней недели, 8 букв, 9
птиц (все объекты перечисляются)».
• Усложнение за счет числа пересчитываемых
названий.
72. Развитие творческого воображения
как процесса создания нового в форме
образа, представления или идеи
73.
Техники:
а) Незаконченные фигуры
б) Составление предложения, рассказа с
использованием определенных слов
в) Завершение рассказа
г) Комбинирование
д) Мысленное конструирование
е) «Географическая карта»
ж) Схематизация и др.
74. «Изучение географической карты + ориентировка в пространстве»
• Ребенку дают «карту» – схему с
изображением какой-либо реки. По берегам
реки нанесены схематические изображения
городов, деревень, железной дороги, мостов
и пр.
• Педагог: «Видишь, по реке плывет теплоход.
Представь себе, что ты стоишь на палубе,
смотришь на берега.
И вот обо всем, что ты
видишь, расскажи».
75. «Незаконченные фигуры» +ориентировка в пространстве и развитие геометрического мышления
• Предложите ребенку
рисунок с разными
незаконченными
изображениями и
попросите его
нарисовать чтонибудь интересное,
используя их.
• Когда ребенок
сделает рисунок,
попросите его
рассказать о том,
что он изобразил.
76. «Точки»
• Покажите детям на
примере, как
можно, соединяя
точки, сделать
рисунок. А теперь
предложите им
самим попробовать
нарисовать что-то,
соединяя точки.
Использовать все
точки каждый раз
не обязательно.
77. Варианты творческого воображения в математической деятельности
1. Комбинирование — сочетание
отдельных элементов разных объектов
в новых комбинациях.
Реализуется в геометрических играх и
упражнениях на трансфигурацию:
• Разделить квадрат на треугольники и
составить из них другую фигур
• Составить домик ( машинку) из
геометрических фигур (палочек)
без образца)
Игра «Танграм»
78. «Комбинирование»
• Детей просят
придумать и
нарисовать как
можно больше
предметов,
используя
геометрические
фигуры и их части:
круг, полукруг,
треугольник,
прямоугольник,
квадрат.
79. Варианты творческого воображения в математической деятельности
2. Схематизация – представление
объекта в виде эталона (схемы) и ,
наоборот, превращение эталона в
реальный объект:
• Изобразить предмет (мячик,
пирамидку, огурец, морковь) в виде
геометрической фигуры;
• Превратить геометрическую фигуру в
предмет, добавив детали.
80. Варианты творческого воображения в математической деятельности
3. Мысленное конструирование объектов
по словесному описанию и их
воссоздание (опознание)
• Представьте фигуру с пятью углами,
нарисуйте ее;
• Найди цифру по описанию «Палочка
и хвостик», «Два крючка: один вверху,
другой внизу»
81. Развитие восприятия
Развитие восприятия математических
объектов и явлений, значимых для
ребенка старшего дошкольного
возраста.
82. Упражнения для развития компонентов процесса восприятия: целостности, дифференцированности, точности
• Упражнение «Узнай, кто это»
(целостность восприятия)
Ребенку показывают фрагмент рисунка
(геометрической фигуры, цифры), по
которому он должен определить то целое
изображение, к которому относятся части.
• Упражнение «Залатай коврик»
(целостность восприятия)
Ребенку предлагается закрыть «дырку» на
коврике подходящей по форме и размеру
«заплаткой»
83. «Дорисуй фигуры» (развитие целостности восприятия)
• Материал: лист с изображением половин
(частей) геометрических фигур.
• Ребенку предлагается дорисовать вторую
половину (часть).
84. Упражнение «Найди такой же» (дифференцированность восприятия)
• Детям показывают рисунок с изображением
10 фигур, 5 из которых совершенно
одинаковые, а 5 – немного отличаются от
них. Например: 5 квадратов и 5
четырехугольников очень похожих на
квадраты (круги и овалы). Предлагают найти
и показать все одинаковые фигуры.
85. Упражнения на развитие восприятия математических объектов и явлений, значимых для детей.
Упражнение на развитие
восприятия геометрических фигур
Ребенку предлагается рисунок с изображением
различных геометрических фигур.
Попросите назвать фигуры, которые знает
ребенок, подскажите ему названия тех фигур,
которые он еще не знает.
В следующий раз попросите его нарисовать те
фигуры, которые вы ему назовете (круг, квадрат,
прямоугольник, четырехугольник, треугольник,
эллипс).
86. Упражнения на развитие восприятия пространства
• Упражнение №1
• Ребенку
показывают
картинку и
спрашивают о
расположении
предметов: «Что
нарисовано в
середине, вверху,
внизу, в правом
верхнем углу, в
левом нижнем углу,
в правом нижнем
углу ?»
87.
Упражнение №2
На столе перед ребенком располагают
игрушки следующим образом:
в центре — мишка, справа уточка, слева —
заяц, впереди — кукла, сзади — лиса, и
просят ответить на вопросы о
расположении игрушек: «Где сидит мишка?
Какая игрушка стоит перед мишкой? Какая
игрушка позади мишки? Какая игрушка
стоит слева от мишки? Какая игрушка
справа от мишки?»
88.
Упражнение №3
Ребенка просят на листе бумаги в клетку
нарисовать в центре — большой круг,
слева — квадрат, выше круга —
треугольник, ниже — прямоугольник, над
треугольником — 2 маленьких круга, под
прямоугольником — маленький круг.
Задание ребенок выполняет
последовательно.
89. Упражнения №4, №5
• №4 Попросите ребенка
соединить точки так,
чтобы получились
квадраты: самый большой
и самый маленький.
Спросите, какие еще
квадраты могут
получиться, какие точки
для этого нужно
соединить.
• №5 Задание: «Саша
может дойти до школы из
дома разными путями, но
каждый путь должен
соединяться точками.
Нарисуй все пути, покажи
самый короткий, и самый
длинный.
90. Упражнение №6 «Снежинки»
• Задание: Ребенку
предлагается
попарно соединить
одинаковые круги,
чтобы получилась
красивая
снежинка. При этом
ребенок должен
называть признаки
кругов, которые
соединяет.
91. Упражнения на развитие восприятия длительности времени
• Попросите ребенка посидеть тихо в течение
1 минуты. Когда минута, по его мнению,
пройдет, он должен сообщить об этом
(ребенок не должен видеть часы).
• Предлагаете ему проделать три задания,
каждое — за 1 минуту:
— разрезать бумагу ножницами на полоски —
3 см шириной (лист бумаги, разлинованный
по ширине);
— рисовать какие-нибудь фигуры;
— перенести палочки с одного стола на
другой и сложить их в коробочку.
• Каждый раз даете команду к началу
действия, а ребенок сам должен прекратить
выполнение, как только, по его мнению,
минута прошла.
92. Использование специальных развивающих пособий
Как средства развития
познавательного интереса к
математике, математических
способностей детей.
93. ЛОГИЧЕСКИЕ БЛОКИ ДЬЕНЕША
Логический материал
представляет собой набор
из 48 логических блоков,
различающихся четырьмя
свойствами:
формой — круглые,
квадратные, треугольные,
прямоугольные;
цветом — красные, желтые,
синие;
размером — большие и
маленькие;
толщиной — толстые и
тонкие.
94.
95.
Использование логических блоков позволяет:
• развить у детей простейшие логические
структуры мышления;
• научить детей решать логические задачи на
разбиение по свойствам;
• развить у детей умение выявлять в объектах
разнообразные свойства, называть их,
адекватно обозначать словом их отсутствие,
абстрагировать и удерживать в памяти одно,
одновременно два или три свойства,
обобщать объекты по одному, двум или трем,
свойствам с учетом наличия или отсутствия
каждого.
96. Варианты игр для детей 3-4 лет
Сначала предлагаются самые простые игры.
1. «Найди все фигуры (блоки), как эта» по цвету
(размеру, форме).
«Найди не такую фигуру, как эта» по цвету (форме,
размеру).
2. Найди все такие, как эта по цвету и форме (форме и
размеру, по размеру и цвету).
• «Найди не такие, как эта» по цвету и размеру (цвету
и форме, по форме и размеру; по цвету, размеру и
форме).
• «Найди такие же, как эта» по цвету, но другой
формы или такие же по форме, но другого цвета и
т.д.
• Усложнение: найди такие же, как эта фигура, по
цвету и форме, но другие по размеру (такие же по
размеру и цвету, но другие по форме и.т.д.).
97. Варианты игр для детей 3-4 лет
• 3. «Цепочка»
От выбранной фигуры постройте как можно
более длинную цепочку.
Варианты построения цепочки:
• чтобы рядом не было фигур одинаковой
формы (цвета, размера, толщины);
• чтобы рядом не было одинаковых по форме и
цвету фигур (по цвету и размеру, по размеру
и форме, по толщине и т.д.);
• чтобы рядом были фигуры одинаковые по
размеру, но разные по форме и т.д.;
• чтобы рядом были фигуры одинакового цвета
и размера, но разной формы (одинакового
размера, но разного цвета).
98. Варианты игр для детей 3-4 лет
4.
«Второй ряд»
Выложить в ряд 5-6 любых фигур. Построить
под ним второй ряд так, чтобы:
• под каждой фигурой верхнего ряда
оказалась фигура другой формы (цвета,
размера);
• такой же формы, но другого цвета (размера);
• другая по цвету и размеру; не такая по
форме, размеру и цвету.
99. Варианты игр для детей 3-4 лет
5.
«Раздели фигуры»
Предложите детям разделить фигуры между
мишкой и зайкой так, чтобы:
• у мишки оказались все красные фигуры.
Вопросы:
— Какие фигуры у мишки? (Все красные).
— А у зайки? (Все не красные).
• чтобы у мишки оказались все круглые;
• чтобы зайцу достались все большие и т.д.
Более сложный вариант:
• Разделите фигуры так, чтобы у мишки
оказались все синие, а у зайки все
квадратные.
100. Варианты игр для детей 5-7 лет
Детям предлагаются игры и упражнения, где
свойства, изображены на карточках.
ЦВЕТ –
РАЗМЕР –
ФОРМА –
ТОЛЩИНА –
101.
102. Варианты игр для детей 5-7 лет
«Мышки-норушки» предполагает отбор
блоков — «запасов на зиму» в норку (коробку)
по определенному признаку (на карточке).
«Заселим домики» Домики заселяются
жильцами – блоками по определенному
признаку или нескольким признакам (желтые,
большие, круглые)
«Кто быстрее спрячет» Детям предлагается
спрятать все красные; толстые; красные и
толстые; синие, квадратные и большие…
Победителями оказываются те, кто первыми
и безошибочно выполнит задания.
103. Варианты игр для детей 5-7 лет
• В последующем дети осваивают
слова и знаки, обозначающие
отсутствие свойства: некрасный,
некруглый, небольшой.
В играх «Переводчики», «Помоги
Незнайке»требуется рассказать Незнайке о блоках,
научить его по-разному рассказывать про цвет,
величину, форму, толщину.
Например, о желтом прямоугольном блоке можно
сказать, что он:
• некрасный и несиний,
• некруглый и нетреугольный,
• нетолстый,
• небольшой.
104. Варианты игр для детей 5-7 лет
• Последующая работа
с детьми направлена
на освоение детьми
умений оперировать
одновременно двумя
свойствами.
«На свою веточку»
Разобраться, где
должны «висеть»
неквадратные и
красные, желтые и
треугольные… блоки.
105. Варианты игр для детей 5-7 лет
«Кто хозяин?». Разложить блоки для
сказочных персонажей в соответствии с
указанными свойствами. «Чебурашка не
любит красные игрушки и не хочет играть с
круглыми. Зайцу нужны красные и
треугольные и т.д.
106.
107. Варианты игр для детей 5-7 лет
Игры с обручами
• Игра с одним обручем
• На полу лежит обруч. Дети по очереди
располагают блоки в соответствии с заданием
ведущего. Например, внутри обруча — все красные
блоки, а вне обруча-все остальные.
• Игра с двумя обручами
• Дети располагают блоки так, чтобы внутри
синего обруча оказались все круглые блоки, а
внутри красного обруча
— все красные.
Проблема: куда положить
красные и круглые?
Их место – в общей
части обручей.
108.
109. Варианты игр для детей 5-7 лет
Игры с обручами
• Игра с тремя обручами. Задача — классификация
блоков по трем свойствам.
• В игре с тремя обручами моделируется
разбиение множества на восемь классов
подмножеств) с помощью
трех свойств ( красные,
квадратные, большие).
110. Варианты использования блоков для развития творческого воображения
Собачка
111.
• Грузовик
112.
• Парусник
113.
114.
115.
116. Счетные палочки Кюизенера
• Цвет и размер, моделируя число, подводят детей к
пониманию абстрактных понятий, как результата
их самостоятельной деятельности.
• Использование «чисел в цвете» развивает у детей
представление о числе на основе счета и
измерения.
117. Игры и упражнения с палочками
• ПОСТРОЕНИЕ ЛЕСТНИЦ
Дети строят лестницы
разной высоты, что
сопровождается
анализом комплекта,
изучением
особенностей палочек.
118. Игры и упражнения с палочками
СОСТАВЛЕНИЕ КОВРИКОВ
• Цель — формирование понятий «столько же»,
о составе чисел, действиях сложения и
вычитания. Варианты:
1.«Составить» ковер, как можно длиннее;
2. «Составить» ковер так, чтобы все полосы в
нем были разного цвета;
3. «Составить» ковер так, чтобы каждая полоса
состояла из палочек одного цвета и т.д.
4. «Сплести» ковер заданного размера (число 9).
Ковер считается законченным, если учтены
все варианты
состава числа.
119. Игры и упражнения с палочками
СОСТАВЛЕНИЕ РИСУНКОВ
120.
121.
122. Игры и упражнения с палочками
Формируется умение соотносить цвет и число.
Например:
• «Покажи палочку 3, какого она цвета?»
«Найди розовую палочку. Какое число она
обозначает?»
• Детям предлагается выложить числовую
лесенку, отыскивая нужное число:
Найди палочку «1». Какого она цвета?
Затем палочку «2» (уточняется цвет) и т.д.
• Составить число из двух меньших чисел.
• Упражнения в вычитании и сложении.
Например, составили число 5. Предлагается от
пяти отнять один (отодвинуть палочку),
определить, сколько останется.
123.
124.
125.
126.
127. Развивающие игры Воскобовича
ГЕОКОНТ
• В народе ее называют «дощечкой с гвоздиками».
Действительно, на фанерном игровом поле закреплены
пластмассовые гвоздики. На гвоздики натягиваются
«паутинки» (разноцветная резинка-продежка), и получаются
контуры геометрических фигур, предметных силуэтов. Дети
создают силуэты по показу взрослого, собственному
замыслу, дети старшего возраста — по схеме-образцу и
словесной модели (на игровое поле «Геоконта» нанесена
координатная сетка).
128.
Квадрат Воскобовича
Игровой квадрат» представляет собой 32 жестких
треугольника, наклеенных на гибкую основу с двух сторон
на некотором расстоянии друг от друга. Благодаря такой
конструкции квадрат легко трансформируется. Квадрат
изготовлен из плотной ткани, на которую с обеих сторон
наклеены треугольники из легкого пластика (можно
плотного картона) контрастных цветов.
Квадрат может быть двухцветным и четырехцветным.
Квадрат можно определенным образом разрезать.
Например, разрез крестом дает необычные объемные
фигуры. Возможны игры с частями Квадрата (например,
подними левый или правый уголок) — своеобразный
пальчиковый театр.
129.
130.
Чудо-крестики представляет из себя планшет (147х208
мм), с вырезанными отверстиями в виде креста (4 шт),
полукруга (2 шт) и круга. Для каждого отверстия есть
вкладыш. Один вкладыш в виде крестика — целый, 3 другие
разрезаны на 2,3 и 4 части.
Предлагается 2 игры:
— Составление крестиков из частей. Легче это делать в
рамке, для усложнения задания можно предложить ребенку
составить крестик на столе.
— Составление различных фигур из деталей вкладышей. В
состав игры входит альбом с изображением 50 фигур.
Можно предложить ребенку придумать свои фигуры.
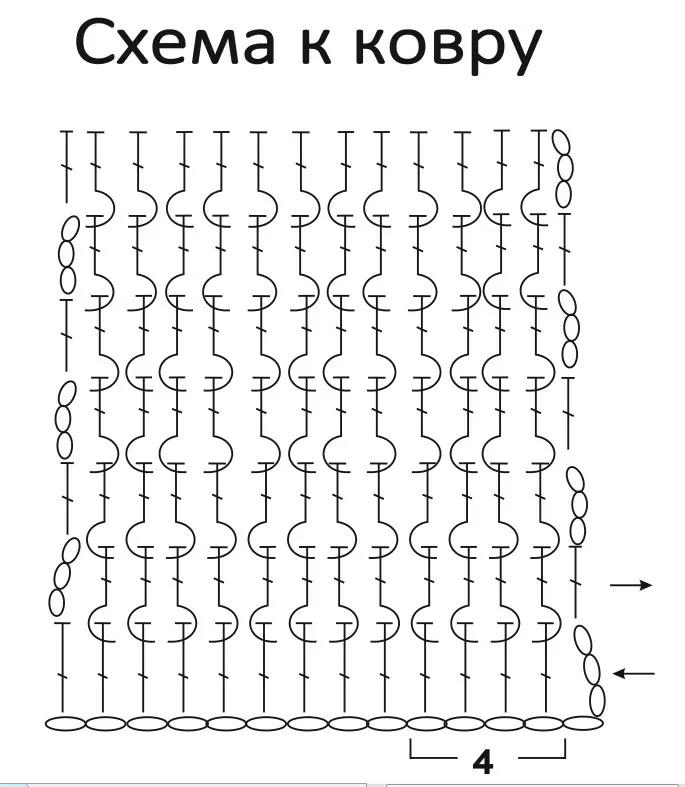
Попробуем решить задачу следующим способом: сначала положим первый ковер: с одной стороны он не закрывает пол на 2 метра (10-8), с другой на 4 метра (10-6). Затем положим третий ковер: он закрыл недостающие 2 метра и вторым слоем лёг на первый.
Теперь положим второй ковёр. От ширины 6 метров отнимем метры, которые лягут вторым слоем, получим, что одна сторона ковра длиной 3 метра легла третьим слоем (два метра легли вторым слоем на третий ковёр и один метр вторым слоем на первый). Определим вторую сторону третьего слоя: первым слоем третий ковёр ляжет на 3 метра (10-7), вторым слоем на длину 1 метр (7-6). Оставшиеся метры лягут третьим слоем: 7 — (3+1)=3.
Получаем, длина одной стороны 3 метра, другой тоже 3 метра, соответственно площадь третьего слоя 3*3=9.
Ответ:9 кв. метров.
Перед вами — ковер Серпинского, это типичный пример фрактальной фигуры. Как и для абсолютного большинства фракталов, ему присуще свойство самоподобия: если мы рассмотрим небольшой фрагмент ковра Серпинского в увеличенном масштабе, то это, в отличие от обычных фигур, не приведет к упрощению рисунка: напротив, откроется столь же сложная картина, что была сначала.
Ковер Серпинского, как и многие другие фракталы, строится итеративно (по шагам) следующим образом. В качестве начального объекта берется квадрат. На первом шаге нужно мысленно разбить этот квадрат на 9 равных квадратиков, а затем (уже не мысленно, а вполне реально) удалить центральный из них (рис. 1, можно не удалять центральный квадрат, а перекрашивать его, если вам так больше нравится). На втором шаге каждый из оставшихся восьми квадратиков также надо мысленно разделить на 9 равных квадратиков, после чего удалить центральный из них. На третьем шаге та же самая операция проводится с каждым из 64 оставшихся квадратиков и так далее до бесконечности. То, что остается в итоге, после завершения этой бесконечной процедуры, и называется ковром Серпинского (этим на первый взгляд парадоксальным словам легко придать строгий смысл: ковер Серпинского состоит из всех точек исходного квадрата, которые не будут вырезаны из него ни на каком из шагов описанной процедуры).
Построенная таким образом фигура обладает рядом интересных и довольно неожиданных свойств. Во-первых, ее площадь равна нулю. В самом деле, пусть, для определенности, длина стороны исходного квадрата равна единице. Тогда:
- на первом шаге выкидывается квадрат, площадь которого равна (frac{1}{3^2});
- на втором шаге выкидываются 8 квадратов, площадь каждого из которых равна (frac{1}{9^2});
- на третьем шаге выкидываются (8^2=64) квадратика, площадь каждого из которых равна (frac{1}{27^2});
- …
Легко видеть, что площади вырезаемых частей образуют геометрическую прогрессию с начальным членом({1}/{9}) и частным ({8}/{9}). Поэтому, суммируя, мы обнаруживаем, что, шаг за шагом выкидывая все больше квадратиков, в конце концов мы вырежем бесконечно много кусков, общая площадь которых составит
[ dfrac{1}{9}left(1+dfrac{8}{9}+left(dfrac{8}{9}right)^2+left(dfrac{8}{9}right)^3+ldotsright) = dfrac{1}{9}cdotdfrac{1}{1-frac{8}{9}}=1. ]
То есть останется фигура площади (1-1=0). Этот же факт можно объяснить еще вот как: площадь оставшейся фигуры на первом шаге равна ({8}/{9}), на втором — (left({8}/{9}right)^2), … На n-м шаге площадь оставшегося куска составит (left({8}/{9}right)^n), и понятно, что при (ntoinfty) эта площадь стремится к нулю.
Таким образом, ковер Серпинского нельзя в полной мере считать плоской фигурой — такие фигуры обычно имеют ненулевую площадь. С другой стороны, кажется интуитивно понятным (и это правда), что он не относится и к семейству кривых, занимая как бы промежуточное положение. Более того, размерность ковра Серпинского оказывается дробной. Об этом читайте в задаче Разные размерности.
Как видно из процесса построения, ковер Серпинского является самоподобной фигурой, то есть его можно разбить на несколько частей, каждая из которых подобна исходной фигуре — на этом наблюдении основывается вычисление ее фрактальной размерности в задаче. Это значит, что к нему, как и к любой самоподобной фигуре, можно применить процесс дефляции-инфляции (см.: Самоподобные замощения). Именно, мы можем разбить ковер Серпинского на восемь ковриков меньшего размера, а затем «раздуть» их в три раза так, чтобы в итоге каждый из этих ковриков сравнялся по размеру с исходной фигурой. Затем опять разбить каждую из частей на 8 ковриков, «раздуть» их до размеров исходного ковра и так далее. Продолжая этот процесс до бесконечности, в пределе мы придем к «замощению» всей плоскости коврами Серпинского (рис. 2). Его можно мыслить, как объединение одного бесконечного дырявого ковра — настолько дырявого, что он занимает нулевую площадь, — и бесконечного набора квадратных заплаток, которыми в этом ковре заполнены все дырки.
Полученное «замощение» обладает как свойствами, типичными для самоподобных замощений, так и свойствами, присущими фрактальным конструкциям. Прежде всего, оно иерархично. Каждый уровень иерархии соответствует некоторой фиксированной длине r, представляющей собой целую степень тройки ((r=3^n), где (ninmathbb{Z})), и фактически вся плоскость разбивается на копии ковра Серпинского со стороной r и «вырезанных» квадратов-заплаток со стороной r (рис. 3). При этом переход на следующий уровень осуществляется разбиением каждого ковра Серпинского на 8 ковриков и 1 заплатку, а каждой заплатки — на 9 квадратов-заплаток меньшего размера, в то время как переход на предыдущий уровень происходит благодаря объединению 8 ковров и 1 заплатки в мегаковер или 9 заплаток в одну мегазаплатку соответственно.
Описанная выше иерархия является строгой в том смысле, что переход с одного уровня на другой может быть произведен единственно возможным способом. Это означает, что для каждого коврика данного уровня иерархии однозначно определена позиция, в которой он входит в ковер предыдущего уровня, — это одна из восьми позиций, показанных на рис. 4. Аналогично, каждая заплатка входит либо в ковер предыдущего уровня на центральной позиции, либо в заплатку предыдущего уровня в одной из 9 позиций.
Как и для любого самоподобного замощения, отсюда следует, что наша картинка является непериодической. Иными словами, ни при каком параллельном переносе ее нельзя совместить с собой. В самом деле, в описанном «замощении» встречаются заплатки размера (3^ntimes3^n) для всех натуральных чисел n. В частности, это означает, что какой бы параллельный перенос мы ни рассмотрели, найдется настолько огромная заплатка, что при этом параллельном переносе она наложится сама на себя, а значит, о самосовмещении не может быть и речи. С другой стороны, практически любой конечный фрагмент этой картинки встретится в ней бесконечно много раз. В самом деле, укрупняя картинку, то есть переходя к предыдущему уровню достаточное число раз, можно добиться того, чтобы искомый фрагмент целиком оказался лежащим внутри некоторого ковра Серпинского размера r. А это значит, что в любом ковре того же размера этот же фрагмент обязательно встретится. Более того, отсюда следует еще одно свойство этого «замощения», типичное для всех фрактальных конструкций: если рассмотреть небольшой его фрагмент в крупном масштабе, то его поведение будет похоже на поведение всей конструкции в целом.
Наконец, аналогично самоподобным замощениям многоугольниками, каждому «замощению» бесконечным ковром Серпинского и набором квадратных заплаток можно сопоставить семейство последовательностей целых чисел. Именно, возьмем произвольный ковер Серпинского A размера 1 и посмотрим, на какой из позиций с рис. 4 он входит в мегаковер — это будет первый элемент последовательности. Затем поглядим, на какой из позиций мегаковер входит в супермегаковер — это будет второй элемент. Продолжая в том же духе, в итоге получим некоторую последовательность ((alpha_n)), составленную из целых чисел от 1 до 8. Если бы мы взяли другой ковер Серпинского B в качестве стартовой точки, мы бы получили другую последовательность, однако ее отличие от ((alpha_n)) заключалось бы только в конечном числе k начальных символов, поскольку для некоторого k существует ковер k-го уровня, который содержит как ковер A, так и ковер B. С другой стороны, мы могли бы начать с ковра размера 3, содержащего A, или с ковра размера 1/3, содержащегося в A — так мы бы получили последовательность, которая отличается от ((alpha_n)) стиранием или добавлением одной цифры соответственно. Как бы то ни было, в данном «замощении» различных ковров Серпинского (в том числе, ковров разных размеров) счетное число, а различных последовательностей из целых чисел от 1 до 8 — континуум. С учетом того, что почти любой последовательности сопоставляется «замощение» плоскости, мы можем заключить, что различных «замощений» континуум. (Существуют исключительные последовательности, которым соответствуют замощения не всей плоскости, а только ее части. Например, последовательность 111111… сопоставляется «замощению» четверти плоскости, а последовательность 131313… — «замощению» полуплоскости; однако вероятность того, что случайно выбранная последовательность окажется исключительной, равна нулю.)
Конструкцию ковра Серпинского легко обобщить на другие фигуры. Если использовать окружности вместо квадратов, то получится так называемая сетка Аполлония. А на рис. 5 показано, что получится, если использовать равносторонний треугольник и шестиугольник (примечательно, что для первого шестиугольника предельное множество получается таким же, как и для треугольника, — с точностью до поворота на (30^{circ}) вокруг центра, а для второго граница искомого множества представляет собой еще один фрактал — снежинку Коха).
Часто она возникает в других математических задачах, на первый взгляд не связанных с самоподобием и фракталами. Рассмотрим, например, знаменитый треугольник Паскаля, составленный из натуральных чисел согласно следующему правилу: в его n-й строке стоит ровно n чисел, крайние из которых равны 1, а каждое из промежуточных представляет собой сумму двух чисел из предыдущей строки, стоящих прямо над ним слева и справа. Оказывается, если мы раскрасим четные числа треугольника Паскаля одним цветом, а нечетные — другим, получится в точности треугольный ковер Серпинского (рис. 6).
Еще один пример возникает в теории клеточных автоматов. Одномерный клеточный автомат представляет собой бесконечную ленту, разделенную на клеточки, каждая из которых окрашена в свой цвет. Каждую секунду каждая клетка перекрашивается по некоторому правилу (своему для каждого конкретного автомата) в зависимости от того, какого цвета были ее соседи в предыдущий момент времени.
Например, клетки автомата, изображенного на рис. 7, раскрашены в два цвета, и на каждом следующем шаге каждая клетка обращается в тот цвет, которым окрашено большинство из ее ближайших соседей, включая ее саму (в этом примере мы предполагаем, что все клетки слева и справа от изображенного куска ленты являются голубыми). Количество цветов, а также количество соседей, влияющих на перекрашивание, вообще говоря, может отличаться для разных клеточных автоматов. В простейшем случае, как в ситуации, упомянутой выше, встречаются клетки только двух цветов, а непосредственное влияние оказывают только соседи, смежные с данной клеткой.
Прикладывая друг к другу ленты, соответствующие состояниям, в которых находился данный автомат в различные моменты времени, мы можем наблюдать динамику процесса. Оказывается, нетрудно придумать автомат, для которого получающаяся картинка при подходящих начальных условиях представляет собой в точности треугольник Серпинского. Действительно, для этого достаточно взять автомат, клетки которого раскрашены в два цвета, и в любой момент времени клетка окрашивается в первый цвет в том и только в том случае, если ровно один из двух ее ближайших соседей имел первый цвет на предыдущем шаге. Остается взять в качестве начального состояния ленту, ровно одна клетка которой покрашена в первый цвет (рис. 8).
Напоследок отметим, что аналогичные конструкции можно соорудить и в пространстве. В зависимости от того, какую именно фигуру мы возьмем в качестве исходной и как именно будем разбивать ее на части, будут получаться различные фракталы. Пожалуй, самые известные примеры — губка Менгера, тетраэдр Серпинского (tetrix), канторова пыль (Cantor dust) и иерусалимский куб (Jerusalem cube).
Рисунки © Хайдар Нурлигареев.
Хайдар Нурлигареев
Если вы увлекаетесь рукоделием, вы должны обязательно знать, как сделать ковёр своими руками. Дело в том, что такое напольное покрытие может не только стать оригинальным украшением вашей комнаты, но и даст вам возможность продемонстрировать своё умение искусной рукодельницы. При этом вы не только сэкономите на покупке достаточно дорогого коврового изделия, но и дадите вторую жизнь старым вещам, из которых будете выполнять ваш коврик.
Содержание
- Назначение самодельных ковриков
- Виды самодельных коров
- Изготовление ковра из ниток
- Изготовление ковра из помпонов
- Создание больших ковров
Назначение самодельных ковриков
Как сделать ковер своими руками вам может подсказать мастер-класс опытного специалиста в области рукоделия. При этом первое, что вы должны решить, ознакомившись с его содержанием, это сфера применения вашего изделия. В зависимости от неё и будет решаться вопрос об использовании для его изготовления того или иного материала, а также применяемая для этого техника.
Так, выделяют 3 основных направления использования самодельных ковровых изделий. Это использование его:
- в качестве декоративного элемента;
- для утепления пола и стен;
- в качестве развивающего элемента.
Если вы только разбираетесь с вопросом о том, как сделать ковер своими руками, вам стоит обратить внимание на создание декоративных ковровых изделий. Дело в том, что они требуют меньше знаний и навыков для выполнения, кроме того, позволяют приложить фантазию и создать ту вещь, которую вы, вполне возможно, не стали бы использовать для утилитарных нужд.
Декоративные изделия можно разместить на стенах, мебели или на полу в специально отведённых местах, для того чтобы создать в помещении атмосферу, присущую тому или иному интерьеру. Кроме того, самодельными ковриками можно оформить салон автомобиля, поместив их, к примеру, на сиденья или обивку салона. Это позволит вам придать оригинальный внешний вид и собственный характер.
Если же знание о том, как сделать ковер своими руками, вам необходимо для выполнения какой-либо утилитарной задачи, например, для создания изделий, служащих утеплителями для пола или стен, нужно будет подобрать специальные материалы, хорошо удерживающие тепло. При этом здесь не подойдёт бумага и иные материалы декоративного назначения. Готовое же изделие можно будет повесить на стену или положить на пол, чтобы в помещении было тепло.
Что же касается развивающих ковриков, то они предназначены для детей, чтобы, играя, они развивались и оттачивали координацию движений. Здесь вам пригодится знание, как сделать ковер из бумаги своими руками. Кроме того, для их создания можно использовать практически любой подручный материал, что значительно удешевляет стоимость такого коврика и позволяет одновременно избавиться от старых вещей.
На заметку! Если же привлечь самих детей к рукоделию и показать им, как сделать ковер самолет своими руками, вы научите их бесценным навыкам, которые потом пригодятся им во взрослой жизни.
При этом такой ковёр ваш ребёнок будет долго хранить в память о вас и о том, как вы приятно провели вместе время, создавая его.
Виды самодельных коров
Для того чтобы понять, как сделать ковер своими руками, необходимо знать виды самодельных ковров, а также технику их изготовления.
Так, в настоящее время популярны следующие виды подобных изделий:
- изготовленные из войлока;
- вязаные;
- созданные из клубков и верёвок;
- плетёные;
- выполненные из обрезков ткани;
- смешанного типа.
Что касается наиболее распространённых самодельных ковровых изделий, то, пожалуй, самыми популярными являются ковры, выполненные в технике вязания крючком. Обычно для этого применяется большой крючок десятого размера и толстые нитки. При этом форма таких ковров может быть практически любой, хотя наиболее востребованы коврики круглой формы.
Вязаные ковры может выполнить любой человек, знакомый с основами вязания крючком, что говорит в пользу этой техники изготовления ковровых изделий. Что же касается их минусов, то обычно такие изделия плохо переносят механические воздействия и быстро истираются. В связи с этим их лучше использовать для укрытия мебели или в декоративных целях.
В России также весьма популярны коврики, изготовленные методом плетения, а также сшивания лоскутков ткани. Это достаточно сложные техники, и если вы хотите узнать, как сделать ковер своими руками подобным образом, вам придётся достаточно долго учиться основам такого мастерства. При этом в итоге вы сможете изготавливать изделия не только для собственных нужд, но и на продажу.
Плетёный коврик выполняется из специальных нитей разного цвета. Для этого набирается основа, сквозь которую позже протягиваются цветные нити, образующие тот или иной узор. При этом опытный мастер может выполнить плетение как в форме круга, так и прямоугольника.
Что касается лоскутных ковриков, то их обычно шьют из остатков различных тканей. Если при этом брать подручные материалы, то просто прекрасные изделия получаются из лоскутков трикотажных футболок. Они режутся на кусочки и сшиваются согласно выбранной вами трикотажной схеме, при этом само изделие может быть как однотонным, так и цветным.
Кстати, лоскутный ковёр можно выполнить из остатков самих ковров или же ковролина. В этом случае материал также режется на части и сшивается. В результате получается изделие, которое нельзя нигде купить.
Что касается других техник, то они менее распространены, и если вы, например, захотели понять, как сделать денежный ковер своими руками, вам придётся достаточно долго разыскивать материал на эту тему.
Изготовление ковра из ниток
Сделать ковер своими руками из ниток – станет для начинающих рукодельниц оптимальным вариантом, который поможет обучиться изготовлению ковровых изделий. Дело в том, что данная техника является простой в освоении и достаточной для создания вполне серьёзных изделий. Кроме того, нитки – это очень распространённый материал и найти их не составит большого труда.
Обычно на ковровое изделие небольшого размера уходит не более 2-3 часов, в результате вы получите весьма оригинальное и уникальное изделие, которое невозможно приобрести в магазине. При этом ваши финансовые затраты будут минимальными – в основном средства нужны на приобретение самих ниток. Использовать же такой коврик можно как в декоративных целях, повесив на стену, так и в практических, например, для защиты мебели от пыли.
Для того чтобы сделать ковер своими руками из ниток, вам необходимо подобрать основу для него. Наиболее распространённым вариантом такой основы может стать филейная сетка. Кроме того, иногда используют строительную арматурную сеть из геотекстиля или самодельную плетёную основу из жгута и льняных ниток.
Если вы решите связать такую сетку самостоятельно, то вам придётся взять льняные нитки и в процессе их вязки делать столбики с накидом, а также выполнить две воздушные петли путём их чередования. Если же вы решите купить филейную сетку, то сможете её найти в любом магазине строительных материалов. Для начинающих рукодельниц это можно считать оптимальным вариантом.
Непосредственно для плетения нужны будут нитки длиной примерно 10 см. Их необходимо будет разрезать, намотав предварительно на любой твёрдый прямоугольный предмет. Разрезы выполняются с каждой стороны такого предмета
Далее берётся толстый крючок, и к каждой ячейке сетки прикрепляются сложенные пополам нитки. После этого нитки захватывают с помощью крючка и протягивают в соседнюю ячейку. Хвостики ниток при этом протягивают в петли и затягивают. Такой плетёный коврик должен у вас получиться без труда.
Для того чтобы выдержать расцветку и рисунок на таком ковре, необходимо заранее нарисовать его схему. Также их можно взять готовые, скачав в интернете. При этом в данной технике допускается использование в качестве основы брезента, холста, мешковины и рогожи. Они придадут всему изделию неповторимый «народный» вид.
Изготовление ковра из помпонов
Многие также спрашивают, как сделать ковер из помпонов своими руками. Тут тоже нет ничего сложного и каждая рукодельница, умеющая вязать, без труда справится с этим заданием. При этом материал для такого коврика – простая пряжа разных цветов.
Здесь так же для создания основы потребуется связанная крючком сетка, на которую и будут крепиться помпоны. Для их изготовления вам понадобится плотный картон. Все же основные работы по изготовлению данного коврового изделия состоят из следующих этапов:
- Вырезают круга необходимого диаметра. В нём точно посередине делают отверстие диаметром меньше. Такие детали выполняют парами.
- Пряжу наматывают на картонное кольцо, продевая иглу между пряжей и картоном.
- После того как вы обмотаете картонное кольцо пряжей, последнюю нить нужно будет закрепить и вынуть из иглы.
- Пряжу с внешней стороны двух колец разрезают ножницами.
- Два кольца разделяют и посередине пряжу перевязывают ниткой.
- Убирают картон, а сам помпон крепко завязывают, оставляя нитки для перевязки длинными.
- Готовые помпоны оформляют, подравнивая нити ножницами.
Кроме того, техника, разрешающая вопрос о том, как сделать ковер своими руками из помпонов, предусматривает изготовление основы изделии из вязанной сетки. Для этого выполняют набор из 4 воздушных петель, которые соединяются при помощи соединительного столбика. При её вязании используют круговую схему.
Начиная от центра цепочки, столбики без накида привязывают 8 раз. Потом провязывают ещё по 2 столбика так же – без накида, пропуская их сквозь каждую петлю первого ряда. Далее происходит вязка одного столбика на одной петле опять без накида, на другой петле. Такая схема в дальнейшем должна чередоваться.
Последним этапом вязки является провязывание петель аналогично схеме третьего ряда, но выполняется такая операция на двух петлях. В последующих рядах происходит увеличение промежутка на несколько столбиков. Окончательным результатом такой работы должно стать изготовление первого круга на 19 рядов. После этого выполняют второй круг, при этом на одном из них закрепляют помпоны, протаскивая их через выполненные ранее отверстия.
Каждый помпон нужно будет привязать с изнанки коврика крепкими узлами. Ненужные нитки при этом обрезают, а с изнаночной стороны пришивается вторая заготовка. После этого можно будет считать, что коврик готов к использованию.
Создание больших ковров
Многие рукодельницы, научившись создавать небольшие изделия, спрашивают о том, как сделать большой ковёр своими руками. Здесь можно отметить, что техника его вязания ничем не отличается от создания небольших ковров, однако трудности в его изготовлении могут возникнуть с выполнением основы таких больших размеров. Кроме того, сама работа будет достаточно длительной и кропотливой.
На заметку! Большие ковры обычно выполняются по размеру помещения, и потом его очень сложно будет использовать в другой квартире или доме.
В связи с этим перед началом работы необходимо точно замерить размеры помещения, в котором ковровое изделие будет располагаться. От этого будет зависеть, насколько точно ковёр подойдёт.
Если же для вас нереально выполнить одно большое изделие, то нет ничего проще, как сделать большой ковёр своими руками, соединив в одно полотно несколько более мелких изделий. Это прекрасный выход для тех рукодельниц, которые не имеют возможности работать в большом помещении. Так они могут работать в условиях маленьких площадей, а готовое изделие сшить из разных кусков уже на месте.
Что же касается сферы использования крупных ковровых изделий, то обычно ими застилают весь пол в комнате. Могут они использоваться и для драпировки стен, а также для оформления веранд. Кроме того, большие ковры могут использоваться для обтяжки мягкой мебели.
К работе над ними стоит приступать, выполнив несколько более скромных по размеру ковровых изделий. Это даст возможность потренировать усидчивость, а также отработать технику плетения или вязания. Научившись выполнять крупные вещи, вы в дальнейшем можете создать собственный малый бизнес на их производстве. Это достаточно прибыльное дело, так как подобные вещи ручного изготовления пользуются большим спросом у населения.
Присоединяйтесь к обсуждению!
Нам было бы интересно узнать вашу точку зрения, оставьте свое мнение в комментариях 😼
1. Методические рекомендации к теме
“Графы”.
Понятие графа целесообразно вводить после
того, как разобрано несколько задач, подобных
задаче 1, решающее соображение в которых –
графическое представление. Важно, чтобы ученики
сразу осознали, что один и тот же граф может быть
нарисован разными способами. Строгое
определение графа, на мой взгляд, давать не нужно,
т.к. оно слишком громоздко и это только затруднит
обсуждение. На первых порах хватит и
интуитивного понятия. При обсуждении понятия
изоморфизма можно решить несколько упражнений
на определение изоморфных и неизоморфных графов.
Одно из центральных мест темы – теорема о
четности числа нечетных вершин. Важно, чтобы
ученики до конца разобрались в ее доказательстве
и научились применять к решению задач. При
разборе нескольких задач рекомендую не
ссылаться на теорему, а фактически повторять ее
доказательство. Чрезвычайно важно также понятие
связности графа. Содержательным соображением
здесь является рассмотрение компоненты
связности, на это необходимо обратить особое
внимание. Эйлеровы графы – тема почти игровая.
Первая и главная цель, которую нужно
преследовать при изучении графов, –научить
школьников видеть граф в условии задачи и
грамотно переводить условие на язык теории
графов. Не стоят рассказывать обе всем на
нескольких занятиях подряд. Лучше разнести
занятия по времени на 2–3 учебных года. (Прилагается
разработка занятия “Понятие графа. Применение
графов к решению задач” в 6 классе).
2. Теоретический материал к теме
“Графы”.
Введение
Графы – замечательные математические объекты,
с их помощью можно решать очень много различных,
внешне не похожих друг на друга задач. В
математике существует целый раздел – теория
графов, который изучает графы, их свойства и
применение. Мы же обсудим только самые основные
понятия, свойства графов и некоторые способы
решения задач.
Понятие графа
Рассмотрим две задачи.
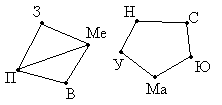
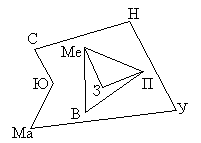
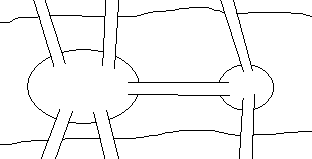
Задача 1. Между девятью планетами
солнечной системы установлено космическое
сообщение. Рейсовые ракеты летают по следующим
маршрутам: Земля – Меркурий; Плутон – Венера;
Земля – Плутон; Плутон – Меркурий; Меркурий –
Вене; Уран – Нептун; Нептун – Сатурн; Сатурн –
Юпитер; Юпитер – Марс и Марс – Уран. Можно ли
долететь на рейсовых ракетах с Земли до Марса ?
Решение: Нарисуем схему условия: планеты
изобразим точками, а маршруты ракет – линиями.
Теперь сразу видно, что долететь с Земли до
Марса нельзя.
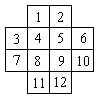
Задача 2. Доска имеет форму двойного
креста, который получается, если из квадрата 4×4
убрать угловые клетки.
Можно ли обойти ее ходом шахматного коня и
вернуться на исходную клетку, побывав на всех
клетках ровно по одному разу ?
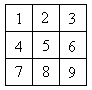
Решение: Занумеруем последовательно
клетки доски:
А теперь с помощью рисунка покажем, что такой
обход таблицы, как указано в условии, возможен:
Мы рассмотрели две непохожие задачи. Однако
решения этих двух задач объединяет общая идея –
графическое представление решения. При этом и
картинки, нарисованные для каждой задачи,
оказались похожими: каждая картинка – это
несколько точек, некоторые из которых соединены
линиями.
Такие картинки и называются графами. Точки
при этом называются вершинами, а линии – ребрами
графа. Заметим, что не каждая картинка такого
вида будет называться графом. Например. если вас
попросят нарисовать в тетради пятиугольник, то
такой рисунок графом не будет. Будем называть что
рисунок такого вида, как в предыдущих задачах,
графом, если есть какая-то конкретная задача для
которой такой рисунок построен.
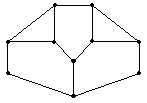
Другое замечание касается вида графа.
Попробуйте проверить, что граф для одной и той же
задачи можно нарисовать разными способами; и
наоборот для разных задач можно нарисовать
одинаковые по виду графы. Здесь важно лишь то,
какие вершины соединены друг с другом, а какие –
нет. Например, граф для задачи 1 можно нарисовать
по-другому:
Такие одинаковые, но по-разному нарисованные
графы, называются изоморфными.
Степени вершин и подсчет числа ребер графа
Запишем еще одно определение: Степенью вершины
графа называется количество выходящих из нее
ребер. В связи с этим, вершина, имеющая четную
степень, называется четной вершиной,
соответственно, вершина, имеющая нечетную
степень, называется нечетной вершиной.
С понятием степени вершины связана одна из
основных теорем теории графов –теорема о
честности числа нечетных вершин. Докажем ее мы
немного позднее, а сначала для иллюстрации
рассмотрим задачу.
Задача 3. В городе Маленьком 15
телефонов. Можно ли их соединить проводами так,
чтобы каждый телефон был соединен ровно с пятью
другими ?
Решение: Допустим, что такое соединение
телефонов возможно. Тогда представим себе граф, в
котором вершины обозначают телефоны, а ребра –
провода, их соединяющие. Подсчитаем, сколько
всего получится проводов. К каждому телефону
подключено ровно 5 проводов, т.е. степень каждой
вершины нашего графа – 5. Чтобы найти число
проводов, надо просуммировать степени всех
вершин графа и полученный результат разделить на
2 (т.к. каждый провод имеет два конца, то при
суммировании степеней каждый провод будет взят 2
раза). Но тогда количество проводов получится
разным . Но это число не
целое. Значит наше предположение о том, что можно
соединить каждый телефон ровно с пятью другими,
оказалось неверным.
Ответ. Соединить телефоны таким образом
невозможно.
Теорема: Любой граф содержит четное
число нечетных вершин.
Доказательство: Количество ребер графа
равно половине суммы степеней его вершин. Так как
количество ребер должно быть целым числом, то
сумма степеней вершин должна быть четной. А это
возможно только в том случае, если граф содержит
четное число нечетных вершин.
Связность графа
Есть еще одно важное понятие, относящееся к
графам – понятие связности.
Граф называется связным, если из любые две
его вершины можно соединить путем, т.е.
непрерывной последовательностью ребер.
Существует целый ряд задач, решение которых
основано на понятии связности графа.
Задача 4. В стране Семерка 15 городов,
каждый из городов соединен дорогами не менее, чем
с семью другими. Докажите, что из каждого города
модно добраться в любой другой.
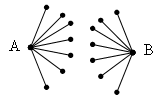
Доказательство: Рассмотрим два
произвольных А и В города и допустим, что между
ними нет пути. Каждый из них соединен дорогами не
менее, чем с семью другими, причем нет такого
города, который был бы соединен с обоими
рассматриваемыми городами (в противном случае
существовал бы путь из A в B). Нарисуем часть графа,
соответствующую этим городам:
Теперь явно видно, что мы получили не менее
различных 16 городов, что противоречит условию
задачи. Значит утверждение доказано от
противного.
Если принять во внимание предыдущее
определение, то утверждение задачи можно
переформулировать и по-другому: “Доказать, что
граф дорог страны Семерка связен.”
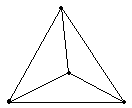
Теперь вы знаете, как выглядит связный граф.
Несвязный граф имеет вид нескольких “кусков”,
каждый из которых – либо отдельная вершина без
ребер, либо связный граф. Пример несвязного графа
вы видите на рисунке:
Каждый такой отдельный кусок называется компонентой
связности графа. Каждая компонента связности
представляет собой связный граф и для нее
выполняются все утверждения, которые мы доказали
для связных графов. Рассмотрим пример задачи, в
которой используется компонента связности:
Задача 5. В Тридевятом царстве только
один вид транспорта – ковер-самолет. Из столицы
выходит 21 ковролиния, из города Дальний – одна, а
из всех остальных городов, – по 20. Докажите, что
из столицы можно долететь в город Дальний.
Доказательство: Понятно, что если
нарисовать граф ковролиний Царства, то он может
быть несвязным. Рассмотрим компоненту связности,
которая включает в себя столицу Царства. Из
столицы выходит 21 ковролиния, а из любых других
городов, кроме города Дальний – по 20, поэтому,
чтобы выполнялся закон о четном числе нечетных
вершин необходимо, чтобы и город Дальний входил в
эту же самую компоненту связности. А так как
компонента связности – связный граф, то из
столицы существует путь по ковролиниям до города
Дальний, что и требовалось доказать.
Графы Эйлера
Вы наверняка сталкивались с задачами, в которых
требуется нарисовать какую-либо фигуру не
отрывая карандаш от бумаги и проводя каждую
линию только один раз. Оказывается, что такая
задача не всегда разрешима, т.е. существуют
фигуры, которые указанным способом нарисовать
нельзя. Вопрос разрешимости таких задач также
входит в теорию графов. Впервые его исследовал в
1736 году великий немецкий математик Леонард
Эйлер, решая задачу о Кенигсбергских мостах.
Поэтому графы, которые можно нарисовать
указанным способом, называются Эйлеровыми
графами.
Задача 6. Можно ли нарисовать
изображенный на рисунке граф не отрывая карандаш
от бумаги и проводя каждое ребро ровно один раз ?
Решение. Если мы будем рисовать граф так,
как сказано в условии, то в каждую вершину, кроме
начальной и конечной, мы войдем столько же раз,
сколько выйдем из нее. То есть все вершины графа,
кроме двух должны быть четными. В нашем же графе
имеется три нечетные вершины, поэтому его нельзя
нарисовать указанным в условии способом.
Сейчас мы доказали теорему об Эйлеровых графах:
Теорема: Эйлеров граф должен иметь не
более двух нечетных вершин.
И в заключение – задача о Кенигсбергских
мостах.
Задача 7. На рисунке изображена схема
мостов города Кенигсберга.
Можно ли совершить прогулку так, чтобы пройти
по каждому мосту ровно 1 раз?
3. Задачи к теме “Графы”
Понятие графа.
1. На квадратной доске 3×3 расставлены 4 коня так,
как показано на рис.1. Можно ли сделав несколько
ходов конями, переставить их в положение,
показанное на рис.2?
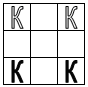
Рис. 1 |
Рис. 2 |
Решение. Занумеруем клетки доски, как
показано на рисунке:
Каждой клетке поставим в соответствие точку на
плоскости и, если из одной клетки можно попасть в
другую ходом шахматного коня, то соответствующие
точки соединим линией. Исходная и требуемая
расстановки коней показаны на рисунках:
При любой последовательности ходов конями
порядок их следования, очевидно, измениться не
может. Поэтому переставить коней требуемым
образом невозможно.
2. В стране Цифра есть 9 городов с названиями 1, 2,
3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два
города соединены авиалинией в том и только в том
случае, если двузначное число, образованное
названиями городов, делится на 3. Можно ли
долететь по воздуху из города 1 в город 9 ?
Решение. Поставив в соответствие каждому
городу точку и соединив точки линией, если сумма
цифр делится на 3, получим граф, в котором цифры 3,
5, 9 связаны между собой, но не связаны с
остальными. Значит долететь из города 1 в город 9
нельзя.
Степени вершин и подсчет числа ребер.
3. В государстве 100 городов к из каждого города
выходит 4 дороги. Сколько всего дорог в
государстве.
Решение. Подсчитаем общее количество
выходящих городов дорог – 100 . 4 =
400. Однако при таком подсчете каждая дорога
посчитана 2 раза – она выходит из одного города и
входит в другой. Значит всего дорог в два раза
меньше, т.е. 200.
4. В классе 30 человек. Может ли быть так, что 9
человек имеют по 3 друга, 11 – по 4 друга, а 10 – по 5
друзей ?
Ответ. Нет (теорема о четности числа
нечетных вершин).
5. У короля 19 вассалов. Может ли оказаться так,
что у каждого вассала 1, 5 или 9 соседей ?
Ответ. Нет, не может.
6. Может ли в государстве, в котором из каждого
города выходит ровно 3 дороги, быть ровно 100 дорог?
Решение. Подсчитаем число городов. Число
дорог равно числу городов х, умноженному на 3
(число выходящих из каждого города дорог) и
разделенному на 2 (см. задачу 3). Тогда 100 = Зх/2 =>
Зх=200, чего не может быть при натуральном х. Значит
100 дорог в таком государстве быть не может.
7. Докажите, что число людей, живших когда-либо
на Земле и сделавших нечетное число рукопожатий,
четно.
Доказательство непосредственно следует из
теоремы о четности числа нечетных вершин графа.
Связность.
8. В стране из каждого города выходит 100 дорог и
из каждого города можно добраться до любого
другого. Одну дорогу закрыли на ремонт. Докажите,
что и теперь из любого города можно добраться до
любого другого.
Доказательство. Рассмотрим компоненту
связности, в которую входит один из городов,
дорогу между которыми закрыли. По теореме о
четности числа нечетных вершин в нее входит и
второй город. А значит по-прежнему можно найти
маршрут и добраться из одного из этих городов в
другой.
Графы Эйлера.
9. Имеется группа островов, соединенных мостами
так, что от каждого острова можно добраться до
любого другого. Турист обошел все острова, пройдя
по каждому мосту розно 1 раз. На острове
Троекратном он побывал трижды. Сколько мостов
ведет с Троекратного, если турист
а) не с него начал и не на нем закончил?
б) с него начал, но не на нем закончил?
в) с него начал и на нем закончил?
10. На рисунке изображен парк, разделенный на
несколько частей заборами. Можно ли прогуляться
по парку и его окрестностям так, чтобы перелезть
через каждый забор розно 1 раз?