Задача по навигации как найти

ГлавнаяБиблиотека # Library Аттестация # AttestationКурсантамРешение общих задач по навигации

< Назад
Вперёд >

Решение общих задач по навигации

Скачать PDF — 0,7 Mb

Источник

Поиск пути среди круглых препятствий

Время на прочтение
9 мин

Количество просмотров 13K

Навигация по лесу

Алгоритм поиска пути A* — это мощный инструмент для быстрой генерации оптимальных путей. Обычно A* демонстрируют при навигации по картам из сеток, но он может использоваться не только для сеток! Он может работать с любыми графами. Можно использовать A* для поиска пути в мире круглых препятствий.

В оригинале статьи все изображения интерактивны.

Как один алгоритм решает обе эти задачи? Давайте начнём с краткого описания того, как работает A*.

Алгоритм A*

Алгоритм A* находит оптимальный путь из начальной в конечную точку, избегая по дороге препятствия. Он реализует это, постепенно расширяя множество частичных путей. Каждый частичный путь — это серия шагов от начальной точки до какой-то промежуточной точки на дороге к цели. В процессе работы A* частичные пути становятся всё ближе конечной точке. Алгоритм прекращает работу тогда, когда находит полный путь, который лучше оставшихся вариантов, и это можно доказать.

На каждом шаге алгоритма A* оценивает множество частичных путей и генерирует новые пути, расширяя наиболее многообещающий путь из множества. Для этого A* хранит частичные пути в очереди с приоритетами, отсортированном по приблизительной длине — истинной измеренной длине пути плюс примерное оставшееся расстояние до цели. Это приближение должно быть недооценкой; то есть приближение может быть меньше истинного расстояния, но не больше него. В большинстве задач поиска пути хорошей преуменьшенной оценкой является геометрическое расстояние по прямой от конца частичного пути до конечной точки. Истинный наилучший путь до цели от конца частичного пути может быть длиннее, чем это расстояние по прямой, но не может быть короче.

Когда A* начинает работу, очередь с приоритетами содержит всего один частичный путь: начальную точку. Алгоритм многократно удаляет из очереди с приоритетами наиболее многообещающий путь, то есть путь с наименьшей приблизительной длиной. Если этот путь завершается в конечной точке, то алгоритм выполнил задачу — очередь с приоритетами гарантирует, что никакой другой путь не может быть лучше. В противном случае, начиная с конца частичного пути, который он удалил из очереди, A* генерирует ещё несколько новых путей, делая единичные шаги во всех возможных направлениях. Он помещает эти новые пути снова в очередь с приоритетами и начинает процесс заново.

Граф

A* работает с графом: набором узлов, соединённых рёбрами. В мире на основе сетки каждый узел обозначает отдельную ячейку сетки, а каждое ребро — соединение с соседними ячейками к северу, югу, востоку или западу.

Прежде чем можно будет запустить A* для леса из круглых препятствий, нам нужно преобразовать его в граф. Все пути через лес состоят из перемежающихся отрезков прямых и дуг. Они являются рёбрами графа пути. Конечные точки этих рёбер становятся узлами.

Путь через граф — это серия узлов, соединённых рёбрами:

И отрезки, и дуги являются рёбрами графа. Мы назовём отрезки рёбрами перехода, потому что путь использует их для перехода между препятствиями. Дуги мы назовём огибающими рёбрами, потому что их задача в пути — огибание сторон препятствий.

Далее мы исследуем простой способ преобразования леса с препятствиями в граф: сгенерируем все возможные рёбра перехода и огибающие рёбра.

Генерация рёбер перехода

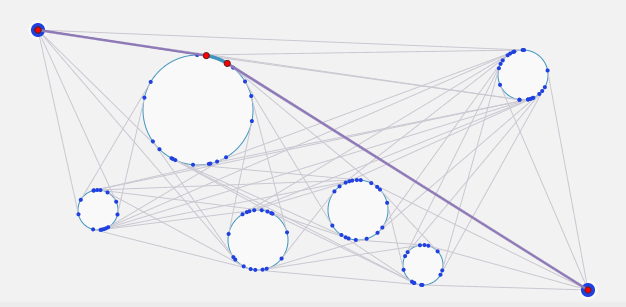
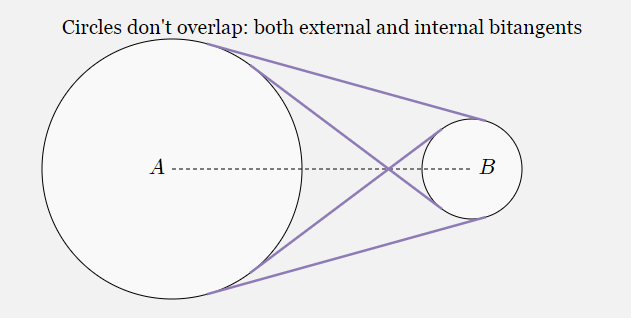
Рёбра перехода между парой кругов — это отрезки прямых, которые едва касаются обоих кругов; такие отрезки называются касательными к двум точкам, и для каждой пары кругов существует четыре таких касательных. Касательные к двум точкам, пересекающиеся между кругами, называются внутренними касательными к двум точкам, а проходящие снаружи — внешними.

Внутренние касательные к двум точкам

В прошлом поиск внутренних касательных был важен для вычисления длины ремня, соединяющего два шкива разного размера, поэтому задача создания внутренних касательных к двум точкам называется задачей ремней. Для нахождения внутренних касательных к двум точкам нужно вычислить угол

$theta$ на показанном ниже чертеже.

Как оказалось, для кругов с центрами

$A$ и

$B$ и радиусами

$r_A$ и

$r_B$, центры которых находятся на расстоянии

$d$:

$theta = arccos{{r_A+r_B}over{d}}$

Определив

$theta$, мы можем легко найти точки

$C$,

$D$,

$E$ и

$F$.

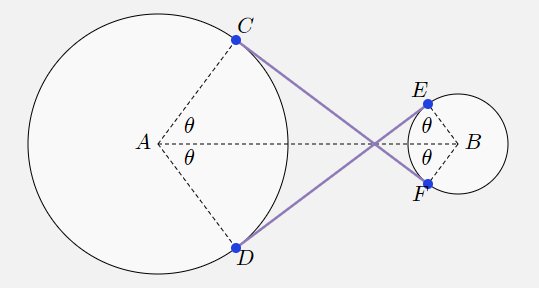
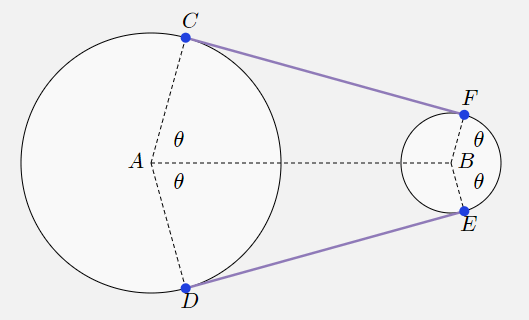
Внешние касательные к двум точкам

При построении внешних касательных (это задача шкивов) используется похожая техника.

Для внешних касательных мы можем найти

$theta$ следующим образом:

$theta = arccos{{lvert r_A - r_B rvert} over d}$

Не важно, какой из кругов больше, A или B, но как видно из рисунка,

$theta$ откладывается на стороне A, ближней к B, но на стороне B, дальней от A.

Линия видимости

Взятые вместе, внутренние и внешние касательные к двум точкам между двумя кругами образуют рёбра перехода между кругами. Но что если одно или несколько рёбер перехода закрывает третий круг?

Если ребро перехода перекрыто другим кругом, то нам нужно отбросить это ребро. Для распознавания такого случая мы используем простое вычисление расстояния между точкой и прямой. Если расстояние от ребра перехода до центра препятствия меньше радиуса препятствия, то препятствие перекрывает ребро перехода, поэтому мы должны его отбросить.

Для вычисления расстояния от точки

$C$ до отрезка прямой

$overline{AB}$ воспользуемся следующим способом:

Во-первых, вычислим

$u$ — часть расстояния вдоль отрезка

$overline{AB}$, в которой перпендикуляр пересекает точку

$C$:

$u = {(C - A) cdot (B-A) over (B-A)cdot(B-A)}$

Затем вычисляем позицию

$E$ на

$overline{AB}$:

$E = A + mathrm{clamp}(u, 0, 1) * (B - A)$

Расстояние

$d$ от

$C$ до отрезка

$overline{AB}$ — это расстояние от

$C$ до

$E$:

$d = |E - C|$

Так как

$d < r$, круг перекрывает линию видимости из

$A$ в

$B$, и ребро необходимо отбросить. Если

$d ge r$, то линия видимости из

$A$ в

$B$ существует, и ребро следует оставить.

Генерация огибающих рёбер

Узлы графа соединяют ребро перехода с огибающим ребром. В предыдущих разделах мы сгенерировали рёбра перехода. Для генерации огибающих рёбер мы начнём с конечной точки ребра перехода, обойдём круг и закончим в конечной точке другого ребра перехода.

Для нахождения множества огибающих рёбер круга сначала найдём все касающиеся круга рёбра перехода. Затем создадим огибающие рёбра между всеми конечными точками рёбер перехода на круге.

Соединяем всё вместе

Сгенерировав рёбра перехода, огибающие рёбра и узлы, а затем отбросив все перекрытые рёбра перехода, мы можем создать граф и запустить поиск пути с помощью алгоритма A*.

Усовершенствования

Рассмотренная нами процедура генерации графа достаточно хорошо работает для объяснения алгоритма, но во многих аспектах может быть улучшена. Такие улучшения позволят алгоритму тратить меньше ресурсов процессора и памяти, а также обрабатывать больше ситуаций. Давайте рассмотрим некоторые из ситуаций.

Препятствия, которые касаются друг друга

Вы могли заметить, что в показанных выше примерах круглые препятствия не накладывались друг на друга и даже не касались. Если допустить, что круги могут касаться друг друга, то это немного усложняет задачу поиска пути

Касательные к двум точкам

Вспомним, что касательные к двум точкам можно найти с помощью этой формулы для внутренних касательных:

$theta = arccos{{r_A+r_B}over{d}}$

и формулы для внешних касательных:

$theta = arccos{{lvert r_A - r_B rvert} over d}$

Когда два круга касаются друг друга или пересекаются, то между ними нет внутренних касательных. В таком случае

${r_A+r_B}over d$ больше единицы. Так как значение арккосинуса за пределами области определения

$[-1, 1]$ не определено, перед нахождением арккосинуса важно выполнять проверку пересечения кругов.

Аналогично этому, если один круг полностью расположен в другом, то между ними не будет внешних касательных. В таком случае

${r_A - r_B} over d$ находится вне интервала

$[-1, 1]$, то есть не имеет арккосинуса.

Линия видимости ребра перехода

Если мы допускаем возможность касания или пересечения препятствий, то в вычислениях линии видимости рёбер перехода возникают новые случаи.

Вспомним вычисление

$u$ — части расстояния вдоль ребра перехода, на котором перпендикуляр к точке касается ребра. Если касание кругов не допускается, то значение

$u$ находится вне интервала

$[0,1]$, то есть круг не может касаться ребра, потому что для этого ему нужно было бы касаться одной из конечных точек ребра. Это невозможно, потому что конечные точки ребра уже являются касательными к другим кругам.

Однако если мы допустим возможность наложения кругов, то значения

$u$ вне интервала

$[0,1]$ смогут перекрывать линию видимости вдоль ребра. Это соответствует случаям, когда круг находится за концом ребра перехода, но перекрывает конечную точку или касается её. Чтобы отслеживать такие случаи математически, мы ограничим

$u$ интервалом

$[0,1]$:

$E = A + clamp(u, 0, 1) * (B - A)$

Линия видимости огибающего ребра

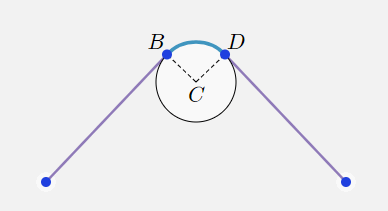
Когда препятствия могут касаться друг друга или пересекаться, огибающие рёбра могут быть заблокированы препятствиями так же, как и рёбра перехода. Рассмотрим огибающее ребро с рисунка ниже. Если огибающего ребра касается другое препятствие, то ребро блокируется и должно быть отброшено.

Чтобы определить, заблокировано ли огибающее ребро другим препятствием, воспользуемся следующим методом для определения точек, в которых пересекаются два круга. Если круги имеют центры в точках

$A$ и

$B$ и радиусы

$r_A$ и

$r_B$, где

$d$ — расстояние между

$A$ и

$B$, то нам для начала нужно проверить несколько случаев. Если круги не касаются друг друга (то есть

$d > r_A + r_B$),
находятся один внутри другого (

$d < |r_A - r_B|$) или совпадают (

$d = 0$ и

$r_A = r_B$), то круги не могут влиять на огибающие рёбра друг друга.

Если не одно из этих условий не соблюдается, то круги пересекаются в двух точках; если круги касаются друг друга, то эти две точки совпадают. Рассмотрим радикальную ось, соединяющую точки пересечения; она перпендикулярна прямой, соединяющей

$A$ и

$B$, в какой-то точке

$C$. Мы можем вычислить расстояние

$a$ от

$A$ до

$C$ следующим образом:

$a = {r_A^2 - r_B^2 + d^2 over 2d }$

Найдя

$a$, мы можем найти угол

$theta$:

$theta = arccos {a over r_A}$

Если

$theta$ равен нулю, то круги касаются в точке

$C$. В противном случае существует две точки пересечения, соответствующие положительному и отрицательному

$theta$.

Далее определим, находится ли какая-нибудь из точек пересечения между начальной и конечной точками огибающего ребра. Если это так, то препятствие блокирует огибающее ребро, и мы должны отбросить это ребро. Заметьте, что нам не нужно рассматривать случай, когда огибающее ребро целиком находится внутри препятствия, потому что отсечение по линии видимости для рёбер перехода уже отбросило это ребро.

После внесения изменений в вычисление касательных к двум точкам и линии видимости для рёбер перехода и огибающих рёбер всё работает верно.

Переменный радиус актора и расширение Минковского

При вычислении навигации круглого объекта в мире круглых препятствий можно учесть наблюдения, упрощающих решение задачи. Во-первых, можно упростить работу, заметив, что движение круга радиусом r по лесу аналогично движению точки через тот же лес с единственным изменением: радиус каждого препятствия увеличивается на r. Это чрезвычайно простой случай применения суммы Минковского. Если радиус актора больше нуля, то перед началом мы просто увеличиваем размер препятствий.

Отложенная генерация рёбер

В общем случае граф для леса из

$n$ препятствий содержит

$O(n^2)$ рёбер перехода, но так как каждое из них нужно проверить на линию видимости с

$n$ препятствиями, то общее время генерации графа равно

$O(n^3)$. Кроме того, пары рёбер перехода могут приводить к созданию огибающих рёбер, и каждое из них нужно проверить с каждым препятствием на линию видимости. Однако из-за высокой эффективности алгоритма A* обычно для создания оптимального пути он просматривает только часть этого большого графа.

Мы можем сэкономить время, генерируя небольшие части графа на лету в процессе выполнения алгоритма A*, а не делая всю работу заранее. Если A* найдёт путь быстро, то мы сгенерируем только малую часть графа. Мы реализуем это, переместив генерацию рёбер в функцию neighbors().

Существует несколько случаев. В начале алгоритма нам нужны соседи начальной точки. Это рёбра перехода от начальной точки к левому и правому ребру каждого препятствия.

Следующий случай — когда A* только что добрался до точки

$p$ на ребре препятствия

$C$ вдоль ребра перехода: neighbors() должна вернуть огибающие рёбра, ведущие из

$p$. Для этого мы определим, какие рёбра перехода выходят из препятствия, вычислив касательные к двум точкам между

$C$ и всеми остальными препятствиями, отбросив все те, которые не находятся на линии видимости. Затем найдём все огибающие рёбра, соединяющие

$p$ с этими рёбрами перехода, отбросив те, которые блокированы другими препятствиями. Возвращаем все эти огибающие рёбра,, сохраняя рёбра перехода для возврата в последующем вызове neighbors().

Последний случай — когда A* обошёл огибающее ребро вдоль препятствия

$C$ и ему нужно покинуть

$C$ по ребру перехода. Так как предыдущий этап вычислил и сохранил все рёбра перехода, можно просто найти и возвратить правильное множество рёбер.

Отсекаем заострённые огибающие рёбра

Огибающие рёбра соединяют рёбра перехода, касающиеся одного круга, но оказывается, что многие из таких огибающих рёбер не подходят для использования в оптимальном пути. Мы можем ускорить алгоритм, устранив их.

Оптимальный путь через лес препятствий всегда состоит из перемежающихся рёбер перехода и огибающих рёбер. Допустим мы входим в узел

$A$ и решаем, как из него выйти:

Вход через

$A$ означает, что мы движемся по часовой стрелке (

$circlearrowright$). Мы должны выйти через узел, который позволяет нам продолжать двигаться по часовой стрелке (

$circlearrowright$), то есть мы можем выйти только через узел

$B$ или

$D$. Если выйти через

$C$, то создастся перегиб (

$curlywedge$) пути, что никогда не будет оптимальным. Нам нужно отфильтровывать такие заострённые рёбра.

Для начала заметим, что A* и так обрабатывает каждое неориентированное ребро

$P longleftrightarrow Q$ как два ориентированных ребра,

$P longrightarrow Q$ и

$Q longrightarrow P$. Мы можем воспользоваться этим, пометив рёбра и узлы ориентацией.

  1. Узлы $P$ становятся узлами с ориентацией — по часовой ($Pcirclearrowright$) или против часовой ($Pcirclearrowleft$) стрелки.
  2. Неориентированные рёбра перехода $P longleftrightarrow Q$ становятся ориентированными рёбрами $P,p longrightarrow Q,hat{q}$ и $Q,q longrightarrow P,hat{p}$, где $p$ и $q$ — это ориентации, а $hat{x}$ означает направление, противоположное $x$.
  3. Неориентированные огибающие рёбра $P longleftrightarrow Q$ становятся ориентированными рёбрами $Pcirclearrowright longrightarrow Qcirclearrowright$ и $Pcirclearrowleft longrightarrow Qcirclearrowleft$. Именно здесь происходит фильтрация: мы не включаем $Pcirclearrowright longrightarrow Qcirclearrowleft$ и $Pcirclearrowleft longrightarrow Qcirclearrowright$, потому что смена направления создаёт перегибы ($curlywedge$).

В нашей схеме узел

$A$ превратится в два узла,

$Acirclearrowright$ и

$Acirclearrowleft$, он имеет входящее ребро перехода

$longrightarrow Acirclearrowright$ и исходящее ребро перехода

$Acirclearrowleft longrightarrow$. Если мы попали на путь через

$Acirclearrowright$, то должны выйти через узел

$circlearrowright$, который будет или ребром перехода

$Bcirclearrowright longrightarrow$ (через огибающее ребро

$Acirclearrowright longrightarrow Bcirclearrowright$), или ребро перехода

$Dcirclearrowright longrightarrow$ (через огибающее ребро

$Acirclearrowright longrightarrow Dcirclearrowright$). Мы не можем выйти через

$Ccirclearrowleft longrightarrow$, потому что так изменится направление поворота, и мы отфильтровали огибающее ребро

$Acirclearrowright longrightarrow Ccirclearrowleft$.

Отфильтровав из графа эти заострённые огибающие рёбра, мы повысили эффективность алгоритма.

Отсечение пересекающих рёбер

Можно отсекать частичные пути, последние рёбра перехода которых пересекают предпоследнее ребро перехода.

Многоугольные препятствия

См. Game Programming Gems 2, Chapter 3.10, Optimizing Points-of-Visibility Pathfinding, написанную Томасом Янгом. В этой главе рассматривается отсечение узлов, но не для кругов, а для многоугольников.

Справочные материалы

  • Задача ремней
  • Задача шкивов
  • Расстояние между точкой и прямой
  • Пересечение двух окружностей
Источник

Подборка задач по навигации с решениями. Полный документ доступен в формате Ворд по запросу. Так же месть другие варианты этой контрольной. Не нашли свой вариант — закажите у нас. Помощь заочникам, обучающимся по специальности морское судовождение.

Содержание:

  1. Задача 17 стр. 2
  2. Задача 25 стр. 3
  3. Задача 40 стр. 4
  4. Задача 55 стр. 5
  5. Задача 60 стр. 7
  6. Задача 66 стр. 8
  7. Задача 121 стр. 9
  8. Задача 158 стр. 10

Список литературы                                                                   стр. 12

Задача 17.

Судно вышло из порта о. Савайи с координатами φ1=13°35.0’S  λ1=172°25.0’W и прибыло в порт. Найти координаты пункта прихода, если координаты: Δφ=14°53.0’кN Δλ=083°47.0’кW

Решение:

φ1=13°35.0’S  (-)

+

Δφ=14°53.0’кN (+)

____________

φ2=01°18.0’N

λ1=172°25.0’W  (-)

+

Δλ=083°47.0’кW (-)

_____________

λ2=256°12.0’W=103°48’E

Порт прихода – Сингапур

Задача 25.

Судно вышло из порта и прибыло в п. Корсаков. Найти координаты пункта отхода, если координаты порта прихода φ2=46°37.0’N  λ2=142°45.0’E Δφ=04°53.0’кS Δλ=142°50.0’кE

Решение:

φ2=46°37.0’N  (+)

—

Δφ=04°53.0’кS (-)

_____________

φ1=51°30.0’N

λ2=142°45.0’E  (+)

—

Δλ=142°50.0’кE (+)

_____________

λ1=000°15.0’W

По координатам определяем, что пункт отхода – порт Лондон.

Задача 40.

Перевести направления из одной системы счета в другие.

  Румбовая Четвертная Полукруговая Круговая
1 WNW NW 67.5 N 67.5 W 292.5
2 ENE NE 67.5 N 67.5 E 67.5
3 NNE NE 22.5 N 22.5 E 22.5
4 NW NW 45.0 N 45.0 W 315.0

Задача 55.

Карта 62272. Условия наблюдений хорошие. Судно РТМС следует ГКК=271.0° (-1.0°) в координатах φ=44°10.0’N  λ1=147°33.0’E Снять с карты координаты точек нахождения судна в моменты открытия г. Мечникова, г. Восточная, мк. Ловцова.

ИК=ГКК+ΔГК=271.0°-1.0°=270.0°

С карты снимает значения высот ориентиров:

г.Мечникова h1=798 м

г. Восточная h2=385 м

С карты снимаем значение Dк мк. Ловцова:

Dк3=22 мили

Из приложения 1 выбираем высоту глаза наблюдателя для РТМС:

е=8.8+1.7=9.5 м

Дальность видимости с высоты глаза наблюдателя:

Полная дальность видимости ориентира:

г. Мечникова мили

г. Восточная мили

мк. Ловцова

Поправка к дальности на высоту глаза наблюдателя:

мили

Расстояние, с которого откроется маяк:

мили

Порядок построения:

1.Отмечаем начальную точку на карте φ=44°10.0’N  λ1=147°33.0’E

2.Из указанной точки строим линию пути судна ИК=270.0°

3.Из каждого ориентира строим окружности, радиусом равным рассчитанным значениям полной дальности до пересечения с линией курса.

4.Снимаем координаты точек пересечения.

г. Мечникова

φ=44°10.0’N  λ1=147°13.5’E (синяя метка)

г. Восточная

φ=44°10.0’N  λ1=147°00.0’E (зеленая метка)

мк.Ловцова

φ=44°10.0’N  λ1=146°58.0’E (красная метка)

Задача 60.

Определить значение магнитного склонения в заданном районе на 2005 год, если с навигационных карт получены и сведены в таблицу необходимые для расчета данные.

Год издания карты Величина склонения на карта в указанном районе Годовое изменение склонения Возраст поправки

лет

 Поправка за количество лет Склонение в 2005 году
1993 (-)17.3 W Увеличение 0.1° 12 -1.2° 18.5 W
1995 (-)9.7 W Уменьшение 0.05° 10 +0.5° 9.2 W
1991 (+)23.0 E Увеличение 6’ 14 +84’ 24.4 E
1986 (+)1.0 E Увеличение 0.2° 19 +3.8° 4.8 E
2000 (+)43.8 E Уменьшение 0.05° 5 -0.25° 43.6 E
2005 (-)12.4 W Уменьшение 0.25° 0 0 12.4 W
1995 (-)1.0 W Увеличение 0.1° 10 -1.0° 2.0 W
1995 (+)1.0 E Уменьшение 0.2° 10 -2.0° 1.0 W
1995 (-)1.0 W Уменьшение 0.2° 10 +2.0° 1.0 E

Задача 66.

Пользуясь данными приложений 3, 4 и таблицей 6 определить d, δ, ΔMK, KK. Плавание в 2005 году.

Номер карты 362-у

ГКК=99.0°

ΔГК=-2.5°

Из приложения 3:

Год издания карты 1998

Склонение с карты  17.1°E

Годовое изменение склонения уменьшение 0.3°

Определяем возраст поправки: 2005год-1998год=7 лет

Склонение в 2005 году 17.1°Е-0.3°*7=15.0°Е

ИК=ГКК-ΔГК=099.0°+2.5°=101.5°

МК=ИК-d=101.5°-15.0°=086.5°

δ=-2.5° (Приложение 4 по МК=086.5°)

ΔМК=δ+d=-2.5°+15.0°=12.5°

КК=МК-δ=086.5°+2.5°=089.0°

Задача 121.

Плавание в Тихом океане в 2005 году. Ведется учет влияния NE ветра и течения SE. Одновременно взяты ГКП и ОКП ориентира. Пользуясь приложениями 3, 4 и таблицей 10, определить: ИК, МК, ГКК, ПУα, ПУс, с, ИП, МП, КУ, δ, ΔМК, ΔГК

Номер карты 362-у

КК=231.0°

ГКП=320.0°

ОКП=146.0°

α=7.0°

β=4.0°

Из приложения 3:

Год издания карты 1998

Склонение с карты  17.1°E

Годовое изменение склонения уменьшение 0.3°

Определяем возраст поправки: 2005год-1998год=7 лет

Склонение в 2005 году 17.1°Е-0.3°*7=15.0°Е

δ=2.8° (Приложение 4 по КК=231.0°)

ΔМК=δ+d=2.8°+15.0°=17.8°

МК=КК+δ=231.0°+2.8°=233.8°

ИК=КК-ΔМК=231.0°-17.8°=213.2°

КП=ОКП-180=146.0°-180.0°=326.0°

ИП=КП+ΔМК=326.0°+17.8°=343.8°

ΔГК=ИП-ГКП=343.8°-320.0°=23.8°

ГКК=ИК+ ΔГК=213.2°+23.8°=237.0°

ПУα=ИК+α=213.2°-7.0°=206.2°

ПУс=ПУα+с=206.2°-4.0°=202.2°

с=α+β=-7.0°-4.0°=-11.0°

Задача 158.

Плавание в Японском море в 2005 г. Судно РТМС следует полным ходом. Ведется учет ЮЗ ветра. Снос течением отсутствует. ГКК=289.0°, кл=0.9, d=15.0°E, ΔГК=1.5° В момент времени Тс1=22.30 открылся маяк Аскольд. Сняли отсчет лага ОЛ1=94.6. В момент времени Тс2=23.56 маяк Аскольд находился на траверзе судна. Пользуясь приложениями 1, 2, 4 и таблицей 14 рассчитать на момент времени Тс2=23.56 расстояние до маяка, ОЛ2, КП, КУ на маяк.

Приложение 1

РТМС

Высота мостика 8.8м

V=14.0 уз

Высота глаза наблюдателя e=8.8+1.7=10.5м

Приложение 2

Мк Аскольд Дк=25 мили, h=110 м

Решение:

Полная дальность видимости в момент открытия маяка

Дп=Дe+Дh

Где    Дe— дальность видимого горизонта наблюдателя с высоты глаза e

Дh – дальность видимого горизонта с высоты предмета h

Дп=Дe+Дh=6.74+21.81=28.55 мили

ИК=ГКК+ΔГК=289.0°+1.5°=290.5°

МК=ИК-d=290.5°-15.0°=275.5°

δ=4.5° (Приложение 4 по МК=275.5°)

ΔМК=δ+d=4.5°+15.0°=19.5°

КК=ИК+ΔМК=290.5°+19.5°=310.0°

Промежуток времени между определениями:

ΔТ=Тс2-Тс1=23ч56м-22ч30м=01ч26м=1.43ч

Пройденное расстояние между определениями:

S=V*ΔT=14.0*1.43=20 миль

Разность отчетов лага:

РОЛ=S/кл=20/0.9=22.2

ОЛ2=ОЛ1+РОЛ=94.6+22.2=16.8

Из прямоугольного треугольника:

КУ=90°л.б.

КП=КК+КУ=310.0°-90°=220.0°

Литература

  1. Дмитриев В.И., Григорьев В.Л., Катенин В.А. Навигация и лоция. Учебник для вузов/Под ред. В.И. Дмитриева –М.:ИКЦ «Академкнига», 2004.-471 с.:ил.
  2. Ермолаева Г.Г. Справочник капитана дальнего плавания. – М.: Транспорт, 1988. -248 с.

Источник

  • Просмотров: 9696

Течение – горизонтальное перемещение масс воды в Мировом океане, характеризующееся направлением относительно географического меридиана КТ и скоростью относительно поверхности Земли (морского дна) vТ.

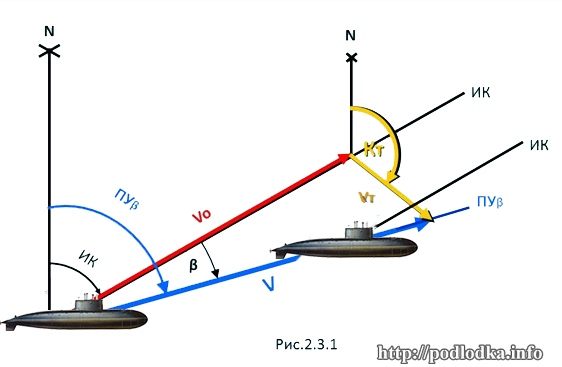
Влияние течения на движение корабля

В районе, где действует течение, движение корабля представляет собой (рис. 2.3.1):

  1. перемещение относительно водной поверхности по линии истинного курса ИК с относительной скоростью VO;
  2. перемещение относительно морского дна под воздействием течения по направлению КТ со скоростью vТ.

Таким образом, корабль перемещается относительно земной поверхности по некоторой линии, которая называется путь при течении ПУβ со скоростью, равной сумме векторов относительной скорости корабля и скорости течения: V = VO + vT, которая называется путевой или абсолютной

Угол между северной частью географического меридиана и линией пути называется путевой угол при течении ПУβ, который определяется выражением:

ПУβ = ИК + β. (2.3.1)

Угол между линией истинного курса ИК и линией пути ПУβ — угол сноса при течении β. Угол сноса β имеет знак плюс, если корабль сносится вправо, минус – сносится влево и определяется из выражения: β = ПУβ — ИК.

По своей природе течения бывают:

  1. постоянные;
  2. приливо-отливные, т. е. их возникновение обусловлено влияниям приливо-образующих сил;
  3. ветровые течения, которые возникают из-за продолжительного воздействия ветра на водную поверхность.

Источниками сведений о течениях являются:

  1. навигационные руководства и пособия, а также морские навигационные карты;
  2. данные о течении (направление и скорость) могут быть получены при совместной работе относительного и абсолютного лагов, а также по информации, получаемой от инерциальных навигационных систем;
  3. направление и скорость течения могут быть вычислены в результате совместной обработки информации методов счисления и обсервации.

Методика учета течения при ручном графическом счислении

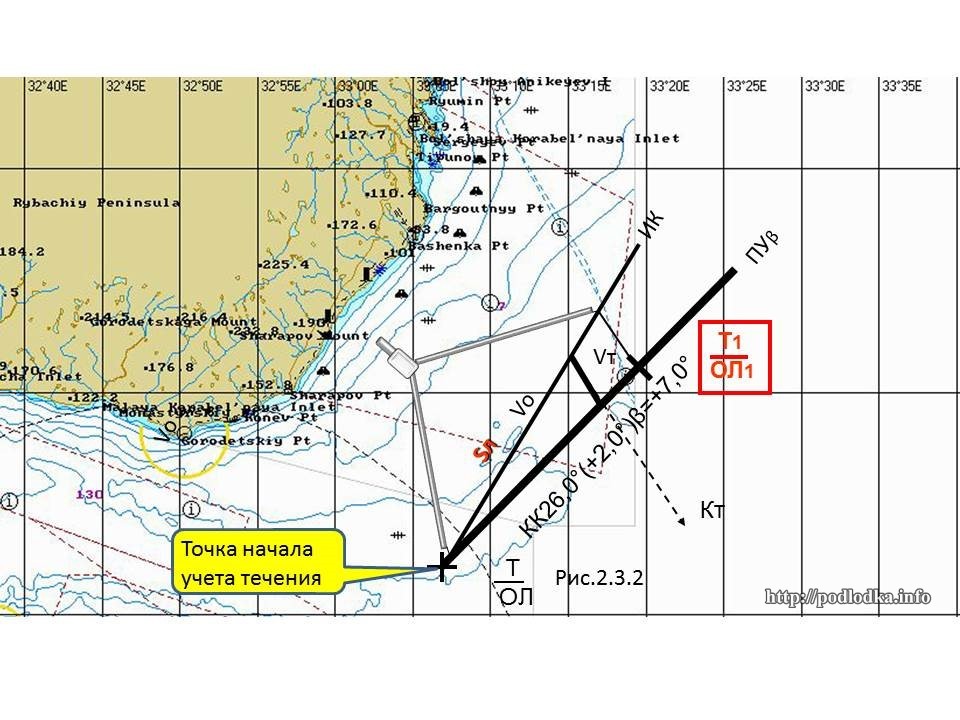
Расчет пути корабля и счислимого места на заданный момент времени (рис. 2.3.2):

  1. Из точки начала учета течения Т/ол на карте проложить линию истинного курса ИК.
  2. На линии истинного курса в масштабе карты отложить вектор относительной скорости корабля VO. Для масштаба выбирают единицы, которые есть на карте, например: 1 узел равен одной минуте широты или долготы.
  3. Из конца вектора относительной скорости по направлению действия течения КТ проложить вектор скорости течения vТ, в том же масштабе, что и VO в п.2.
  4. С помощью параллельной линейки соединить начало вектора относительной скорости VO, точка Т/ол, с концом вектора течения и с помощью транспорти-ра снять направление линии пути ПУβ.
  5. Рассчитать угол сноса β = ПУβ — ИК и на карте у линии пути подписать: КК 26,0 (+2,0) β=+7,0.

Расчет пути корабля и счислимого места на заданный момент времени

Полученный путем графического сложения векторов скоростей треугольник V = VO + vT называется навигационным скоростным треугольником.

Для расчета счислимого места на заданный момент по корабельным часам и счетчику пройденного расстояния лага на заданный момент зафиксировать Т1 и ол1.

Рассчитать пройденное расстояние по относительному лагу: SЛ=(ол1-ол)•kЛ.

Расстояние SЛ отложить на линии истинного курса от точки Т/ол, получен-ную точку снести по направлению действия течения КТ на линию пути – полученная точка Т1/ол1 – счислимое место на заданный момент Т1.

Треугольник характеризующий перемещение корабля относительно водной поверхности по линии ИК, относительно морского дна под действием течения и относительно земной поверхности под действием собственных движителей и течения – треугольник перемещений.

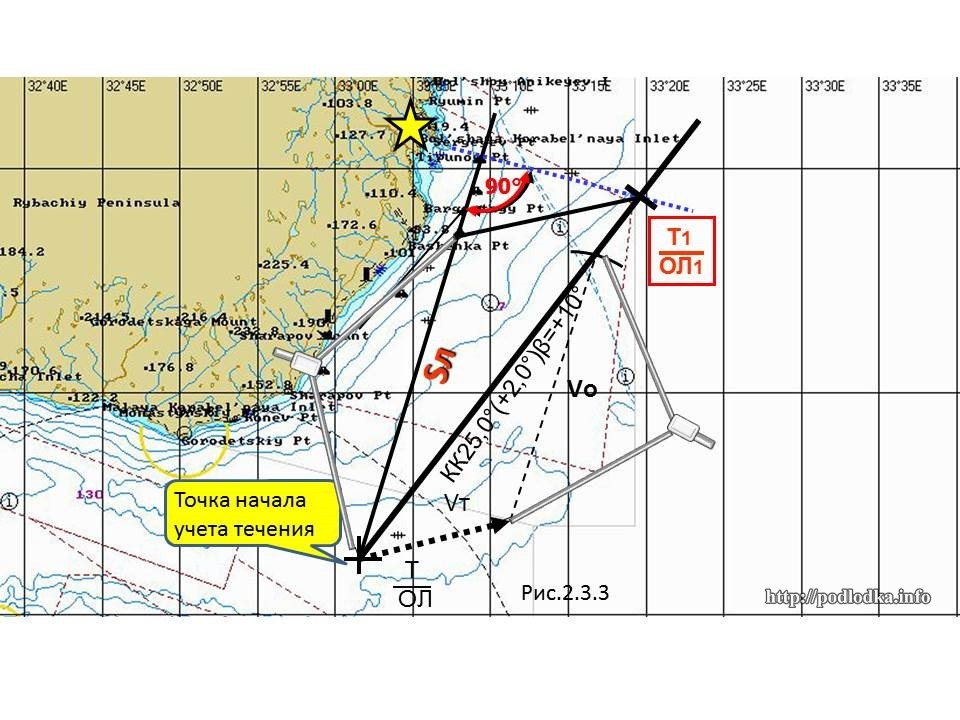
Расчет компасного курса для следования по заданному пути, предвычисление времени Т и отсчета лага ол прихода в назначенную точку (рис. 2.3.3):

  1. Из исходной точки на карте Т/ол проложить линию пути ПУβ, по которой планируется движение корабля
  2. Из этой же точки Т/ол построить вектор течения по направлению КТ в выбранном масштабе.
  3. Из конца вектора течения циркулем, раствор которого равен относительной скорости корабля VO в выбранном масштабе на линии пути сделать засечку.
  4. С помощью параллельной линейки соединить конец вектора течения с засечкой линии пути и транспортиром снять полученное направление линии истинного курса ИК.
  5. С помощью параллельной линейки перенести ИК в точку Т/ол и построить на карте (вспомогательные построения – на рисунке пунктирные линии, после решения задачи с карты стереть).
  6. Рассчитать угол сноса: β = ПУβ — ИК и компасный курс, задаваемый рулевому для следования по заданной линии пути: КК = ИК — ∆К.

Расчет компасного курса для следования по заданному пути, предвычисление времени Т и отсчета лага ол прихода в назначенную точку

Точка на линии пути может назначаться либо по координатам, либо относительно какого-либо объекта (навигационного ориентира) по заданному пеленгу, расстоянию от ориентира, курсовому углу на ориентир, например траверз.

Для предвычисления времени и отсчета лага прихода в заданную точку необходимо (см. рис. 2.3.3):

  1. На линии пути ПУβ построить заданную точку – траверз ориентира: ИП=ИК±90⁰.
  2. Измерить расстояние SЛ, проходимое кораблем по относительному лагу от исходной до заданной точки, для чего через заданную точку на линии пути провести отрезок, параллельный направлению течения до пересечения с линией истинного курса, и измерить расстояние по линии истинного курса от точки Т/ол до точки.
  3. Рассчитать время плавания и рол, на которое изменит показание счетчик пройденного расстояния за время плавания: t = SЛ / VO; рол = SЛ / kЛ
  4. Рассчитать время прихода в назначенную точку и соответствующий от-счет лага: Т1=Т + t; ол1 = ол + рол.

Смотрите также

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти человека на подселение в квартиру
  • Как найти подходящего мужика
  • Как найти рентабельность совокупного капитала
  • Нашел карту сбербанка как ей воспользоваться
  • Как найти спонсора для женщины в москве