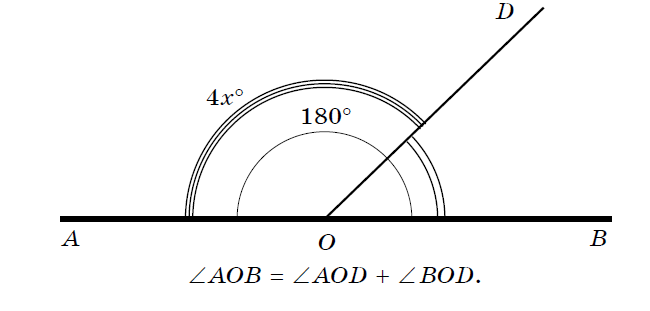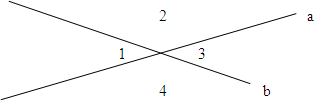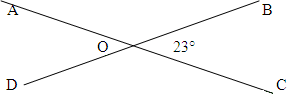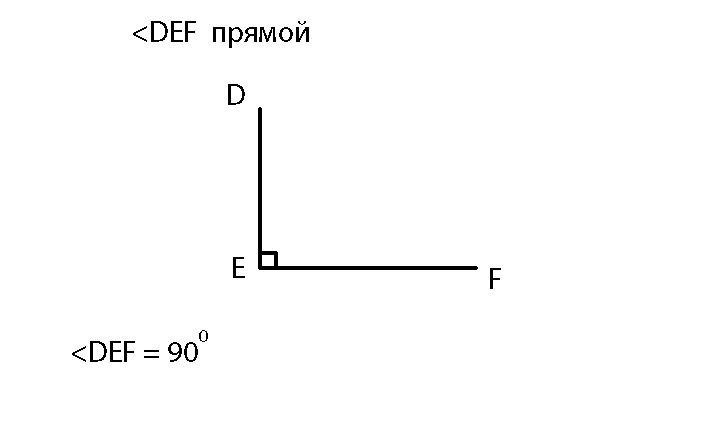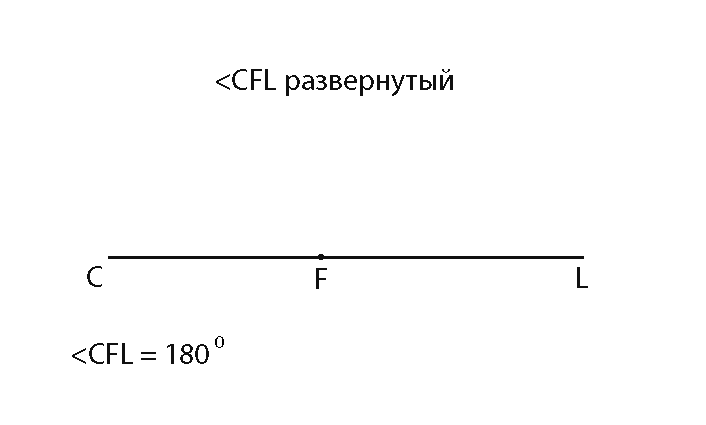Рассказываем, как решать на нахождение градусной меры угла. Приводим алгоритм и примеры решения. Задачи для самостоятельного решения.
Суть задач на нахождение градусной меры угла
Задачи на нахождение градусной меры угла – это геометрические задачи на построение и нахождение величины угла, выраженной в градусах.
Алгоритм решения задач
Алгоритм решения задач на нахождение градусной меры угла:
- Выполняем краткую запись задачи;
- Определяем способ и решаем задачу;
- Выписываем полный ответ.
Определяем способ решения:
Способы решения задач
Примеры решения задачи
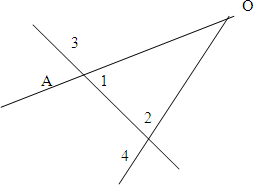
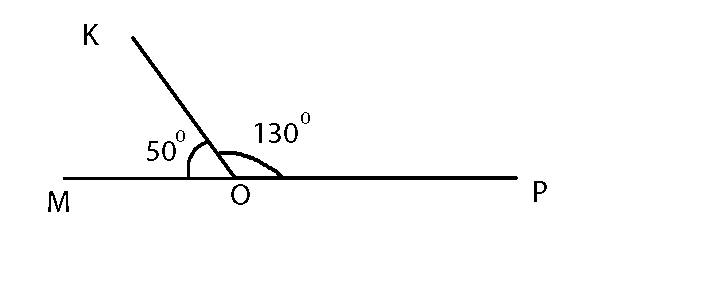
Задача 1. Угол AOB — развернутый. Провели луч OD. Найти градусную меру угла AOD, если угол AOD в 4 раза больше угла BOD.
Краткая запись:
Решение:
- Пусть ∠ BOD = x°, тогда ∠ AOD = 4x°.
Так как их сумма равна 180°, составим и решим уравнение:
(4x+x=180)
(5x=180)
(x=180:5)
(x=36).
Итак, ∠ BOD = 36°, тогда ∠ AOD = 4 ⋅ 36° = 144° (или ∠ AOB = 180° – 36° = 144°).
Ответ: ∠ AOD = 144°.
Задачи для самостоятельного решения
- Луч BD — биссектриса ∠ ABC. Найти градусную меру ∠ DBC, если ∠ ABC = 160°.
- ∠ AOC = 132°, провели луч OB внутри ∠ AOC. Найти градусную меру ∠ AOB, если ∠ BOC = 35°.
- Внутри прямого угла ACB провели луч CD. Найти градусные меры углов ACD и BCD, если разность градусных мер углов ACD и BCD равна 40°.
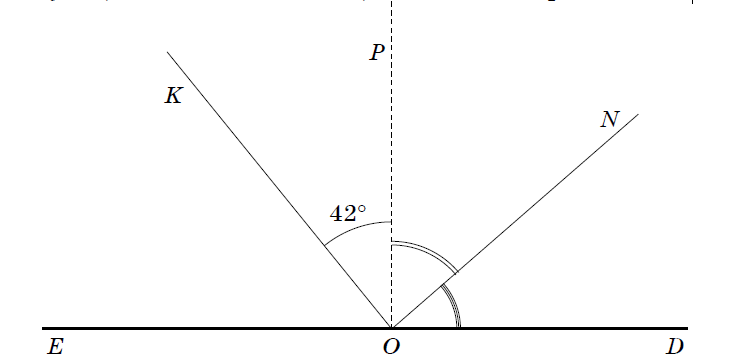
- Определить градусную меру ∠ KON, изображенного на рисунке, если ∠ EOP = ∠ DOP, ON — биссектриса ∠ DOP.
Посмотреть еще в категории: Задачи по математике 5-6 класс
- Задачи на сложение и вычитание
- Задачи на движение навстречу друг другу
- Задачи на движение в одном направлении
- Задачи на движение в противоположных направлениях
- Задачи на движение по реке
- Задачи на нахождение дроби от числа
- Задачи на нахождение числа по его дроби
- Задачи на нахождение процента от числа
- Задачи на нахождение числа по его процентам
- Задачи на процентное отношение двух чисел
- Задачи на проценты (с помощью пропорции)
- Задачи на нахождение периметра и площади треугольника
- Задачи с использованием формул площадей прямоугольника и квадрата
- Задачи на нахождение объема прямоугольного параллелепипеда и куба
- Задачи на проценты
- Задачи на нахождение длины окружности и площади круга
Тип урока: урок закрепления нового материала
Цели урока:
- Образовательные: повторить и закрепить понятия о смежных и вертикальных углах;
- Развивающие: развивать умение анализировать условие задачи;
- Воспитательные: воспитание аккуратности (аккуратное выполнение чертежей на доске и в тетрадях, рациональное распределение записей).
Структура урока:
- I этап. Организационный момент
- II этап. Актуализация опорных знаний
- III этап. Закрепление изученного материала
- IV этап. Зарядка для глаз
- V этап. Самостоятельная работа
- VI этап. Домашнее задание
- VII этап. Итог урока
Ход урока
I. Организационный момент
(Слайд 1-2)
Приветствие, сообщение темы, целей и задач.
Учитель: Вам было задано домашнее задание: повторить п.14 и 15, ответить на вопросы 1, 2, 3, 6, 7. Сейчас проверим, как вы подготовились к уроку.
II. Актуализация опорных знаний
(Слайд 3)
Вопрос: Какие углы называются смежными? (Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны являются дополнительными полупрямыми)
Вопрос. Из рисунка назвать смежные углы. (Ответ: ∠АОВ и ∠ВОС – смежные углы)
Вопрос. Какая сторона у них общая? (Ответ: ОВ – общая сторона.)
Вопрос. Назвать дополнительные полупрямые. (Ответ. ОС и ОА – дополнительные полупрямые.)
(Слайд 4) Вопрос. Какими свойствами обладают смежные углы?
Ответ.
- Сумма смежных углов равна 180° (теорема)
∠1 + ∠2 = 180°
- Если два угла равны, то и смежные с ними углы равны.
- Если угол не развернутый, то его градусная мера меньше 180°.
- Угол, смежный с прямым, есть прямой угол.
(Слайд 5)
Вопросы. Могут ли два смежных угла быть равными:
а) 75° и 80°; Ответ: (нет, т.к.75° + 80°=155°)
б) 94° и 96°; Ответ: (нет, т.к. 94° + 96°= 190°)
в) 83° и 97°? Ответ: (да, т.к. 83° + 97°= 180°)
(Слайд 6)
Устно.
| Дано:
∠АОВ а ∩ АО а ∩ ОВ ∠3 = ∠4 |
Доказательство. 1. ∠3 смежный с ∠1, ∠4 смежный с ∠2 . 2. Т.к. ∠3 = ∠4 (по условию), то ∠1 = ∠ 2, |
|
Доказать ∠1 = ∠2 |
(Слайд 7)
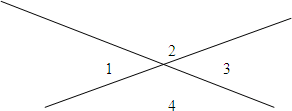
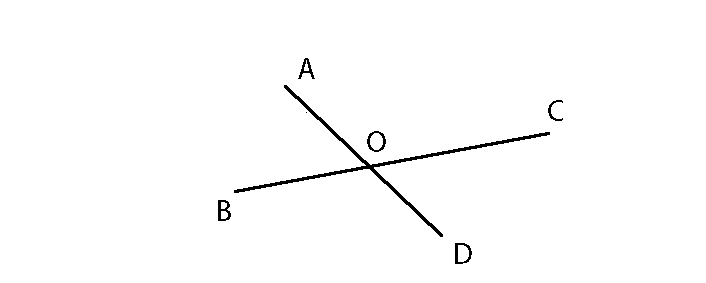
Вопрос. Какие углы называются вертикальными?
(Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого).
∠ 1 и ∠ 3 – вертикальные углы
∠ 2 и ∠ 4 – вертикальные углы
(Слайд 
Вопрос. Каким свойством обладают смежные углы?
Ответ. Вертикальные углы равны. (теорема)
∠ 1 = ∠ 3
∠ 2 = ∠ 4
III этап. Закрепление изученного материала. Решение задач.
(Слайд 9)
№3 (учебник)
|
Дано: ∠1 и ∠2– смежные ∠1 больше ∠2 в 2 раза |
Решение. 1. Пусть ∠2 = х, тогда ∠1=2х 2. Т.к. ∠1 + ∠2 = 180°(по теореме о смежных углах), то х + 2х = 180° 3х = 180°, ⇒ х =180°: 3, х = 60°. 3. Следовательно: ∠2 = 60°, ∠1 = 2∙60°= 120° Ответ: ∠1= 120°, ∠2= 60°, |
| Найти ∠1 и ∠2 |
(Слайд 10)
№6(2)
|
Дано: ∠1 и ∠2 – смежные ∠1 : ∠2 = 3 : 7 |
Решение. 1. Пусть х. – коэффициент пропорциональности. Тогда ∠1 = 3х, ∠2 = 7х (по условию задачи) 2. Т.к ∠1 + ∠2 = 180°(по теореме о смежных углах), то 3х + 7х = 180°, 10х = 180°, х = 18°. 3. Следовательно: ∠1 =3 ∙ 18°=54°, ∠2 =7 ∙ 18°=126° Ответ: 54°; 126°. |
| Найти ∠1 и ∠2 |
(Слайд 11)
|
Дано: ∠1 и ∠2 – смежные ∠2 составляет 0,2 от∠1 |
Решение 1. Пусть ∠1 = х, тогда ∠2 = 0,2х (по условию). 2. Т.к. ∠1 + ∠2 = 180° (по теореме о смежных углах), 3. Следовательно: ∠1=150°, ∠2= 0,2∙ 150°= 30°. Ответ: 150°, 30° |
| Найти ∠1 и ∠2 |
(Слайд 12)
|
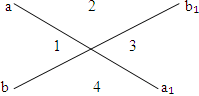
Дано: а ∩ b ∠2 меньше ∠1 в 4 раза |
Решение 1. Пусть ∠2 = х , тогда ∠1 = 4х (по условию), 2. Т.к. ∠1+ ∠2 = 180° (по теореме о смежных углах), 3. Следовательно: ∠2 = 36°, ∠1 = 4∙36° = 144° ∠3= ∠1, ∠4= ∠2 (по теореме о вертикальных углах), Ответ: 144°, 36°, 144°, 36°. |
| Найти ∠1, ∠2, ∠3 и ∠4 |
(Слайд 13)
|
Дано: AС ∩ ВD = O ∠ВОС = 23° |
Решение 1. ∠АОD = ∠ВОС = 23° (по теореме о вертикальных углах) 2. ∠АОВ + ∠ВОС = 180° (по теореме о смежных углах). Следовательно: ∠АОВ =180°– ∠ВОС, 3. ∠СОD = ∠АОВ = 157° (по теореме о вертикальных углах). Ответ: 157°, 157°, 23°. |
|
Найти: ∠СОD, ∠АОВ, ∠АОD. |
(Слайд 14)
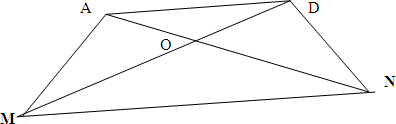
Устно. Вопрос. Назовите смежные и вертикальные углы.
Ответ.
Смежные углы:∠ АОМ и ∠ АОD, ∠АОD и ∠NОD, ∠NОD и ∠NОМ, ∠NОМ и ∠АОМ .
Вертикальные углы: ∠АОМ и ∠NОD, ∠АОD и ∠NОМ.
IV этап. Зарядка для глаз
(Слайд 15)
V этап. Самостоятельная работа (на листочках).
| Вариант 1 | Вариант 2 |
| №1. Один из углов, получившихся при пересечении двух прямых, равен 87°. Найдите остальные углы. | №1. Один из углов, получившихся при пересечении двух прямых, равен 118°. Найдите остальные углы. |
| №2. Разность смежных углов равна 50°. Найдите меньший угол. | №2. Один из смежных углов в 4 раза меньше другого. Найдите больший угол. |
Ответы
| Вариант 1 | Вариант 2 |
| №1. 93°, 87°, 93°. | №1. 62°, 118°, 62° |
| №2. 75°. | №2. 36°. |
VI этап. Домашнее задание.
- §2. Пункты 14-15.
- Задачи на стр. 26. № 6(4), № 12.
VII этап. Итог урока.
- Повторили понятия смежных и вертикальных углов
- Научились решать задачи, используя знания о смежных и вертикальных углах.
- Стали еще на одну ступеньку выше в изучении геометрии.
Теме «Работа с углами треугольника» в ЕГЭ по математике базового уровня традиционно посвящается несколько заданий. В зависимости от предложенных условий учащиеся могут давать как краткий, так и развернутый ответ с полным описанием алгоритма решения. Если вы хотите иметь конкурентные баллы по итогам прохождения ЕГЭ, то вам непременно стоит уделить внимание задачам на нахождение углов треугольника.
В этом вам поможет образовательный портал «Школково». Мы подготовили и изложили базовый теоретический и практический материал таким образом, чтобы все учащиеся, вне зависимости от уровня подготовки, смогли вспомнить основные понятия и без особых затруднений найти углы треугольника в задачах ЕГЭ.
Основные моменты
При решении подобных задач в ЕГЭ можно использовать теорему о сумме углов треугольника. Повторить ее вам поможет наш образовательный ресурс.
Если в условии задачи ЕГЭ не указаны величины внешних углов прямоугольного треугольника, рекомендуется обозначить их переменными. Затем используются известные свойства.
Если решение задачи на нахождение углов равнобедренного или другого треугольника в ЕГЭ не получается выстроить сразу, то, опираясь на полученные данные, необходимо начинать вычислять величины, которые можно найти. При этом учащиеся должны уметь логически выстраивать рассуждение и создавать чертежи.
Научившись правильно выполнять упражнения на нахождение углов равносторонних и других треугольников, а также углов между биссектрисами треугольника, представленные в соответствующих разделах на образовательном портале «Школково», вы сможете закрепить материал и успешно решать подобные задания в ЕГЭ.
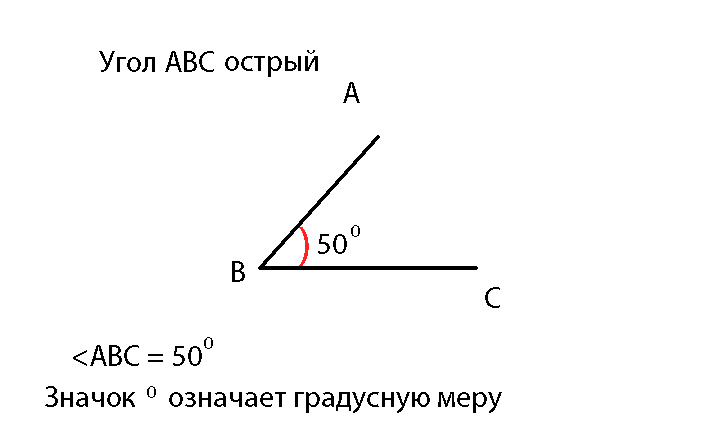
Величина угла измеряется в градусах
По величине (градусной мере) углы бывают:
1. Острые
Острый угол больше 0 градусов,но меньше 90 градусов
2. Прямые
Прямой угол равен 90 градусов
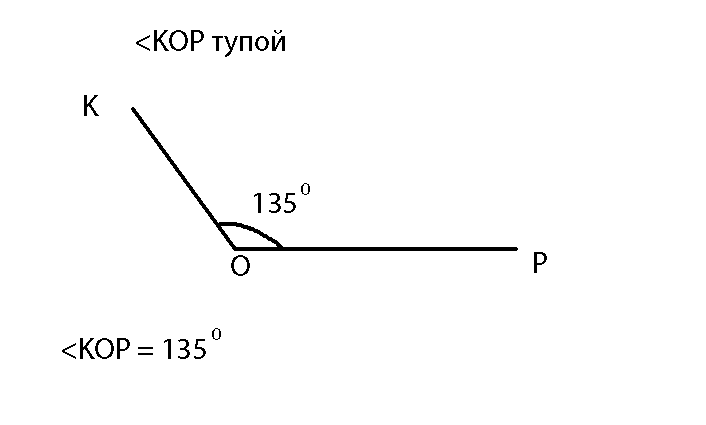
3. Тупые
Тупой угол больше 90 градусов,но меньше 180
4. Развернутые
Развернутый угол равен 180 градусов
По типу взаимного расположения углы бывают:
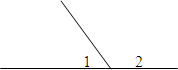
1. Смежные
Сумма смежных углов равна 180 градусов
<KOM и <KOP смежные
Репетитор по геометрии
+7 916 478 10 32
2. Вертикальные
Вертикальные углы равны
<AOB и <COD вертикальные
<AOC и <BOD также вертикальные
1. <ABC = 600 . Найти <CBD, смежный с ним.
Показать решение
2. Один из смежных углов в 2 раза больше другого, найти эти углы.
Показать решение
3. Один из смежных углов в 3 раза больше другого, найти эти углы.
Показать решение
4. Один из смежных углов в 4 раза больше другого, найти эти углы.
Показать решение
5. Один из смежных углов в 5 раз больше другого, найти эти углы.
Показать решение
6. Один из смежных углов на 400 больше другого, найти эти углы.
Показать решение
7. Один из смежных углов на 1000 больше другого, найти эти углы.
Показать решение
8. Один из смежных углов на 100 больше другого, найти эти углы.
Показать решение
9. Один из смежных углов на 300 меньше другого, найти эти углы.
Показать решение
10. Один из смежных углов на 250 меньше другого, найти эти углы.
Показать решение
11. Разность смежных углов равна 400 , найти оба угла.
Показать решение
12. Разность смежных углов равна 1000 , найти эти углы.
Показать решение
13. Разность смежных углов равна 100 , найти эти углы.
Показать решение
14. Разность смежных углов равна 300 , найти эти углы.
Показать решение
15. Смежные углы равны друг другу, найти эти углы.
Показать решение
Содержание:
Основные задачи на построение циркулем и линейкой:
В данном параграфе рассмотрим вопрос о построении геометрических фигур. Вы уже знаете, что геометрические построения можно осуществлять с помощью масштабной линейки, циркуля, транспортира и чертежного угольника. В то же время оказывается, что многие геометрические фигуры можно построить, пользуясь только циркулем и линейкой без масштабных делений.
При построении геометрических фигур с помощью циркуля и линейки без масштабных делений учитывается, что:
- с помощью линейки можно провести произвольную прямую, а также построить прямую, проходящую через две точки;
- с помощью циркуля можно провести окружность произвольного радиуса, а также построить окружность с центром в данной точке и радиусом, равным данному отрезку.
Теперь рассмотрим основные задачи на построение циркулем и линейкой: построение угла, равного данному, построение серединного перпендикуляра к отрезку, построение биссектрисы угла.
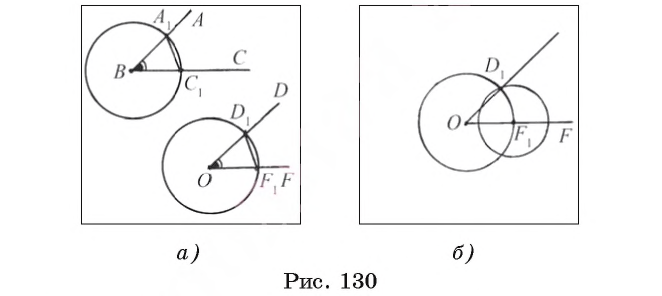
Задача 1 (построение угла, равного данному)
От данного луча OF отложите угол, равный данному углу ABC.
Поиск решения.
Предположим, что угол DOF, удовлетворяющий условию задачи, построен (рис. 130, а).
Пусть
Построение.
1) Строим окружность 
2) Строим окружность 
3) Строим окружность 
4) Пусть D1 — одна из точек пересечения окружностей 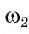



Доказательство.
Равенство 



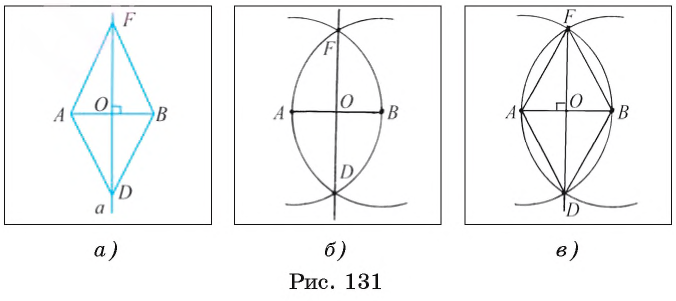
Задача 2 (построение серединного перпендикуляра к отрезку)
Постройте серединный перпендикуляр к данному отрезку АВ.
Поиск решения.
Проведем рассуждения, которые помогут осуществить необходимое построение. Предположим, что серединный перпендикуляр а к отрезку АВ построен (рис. 131, а). Пусть точки F и D лежат на серединном перпендикуляре так, что OF = OD. Прямоугольные треугольники FOB и DOB равны по двум катетам, следовательно, BF = BD. Иначе говоря, точки F и D лежат на окружности 

Построение.
1) Строим окружности 




2) Отмечаем точки F и D пересечения окружностей 

3) Тогда прямая FD — серединный перпендикуляр к отрезку АВ. Докажем это.
Доказательство.
Рассмотрим треугольники FAD и FBD (рис. 131, в). Указанные треугольники равны по трем сторонам. Следовательно, 

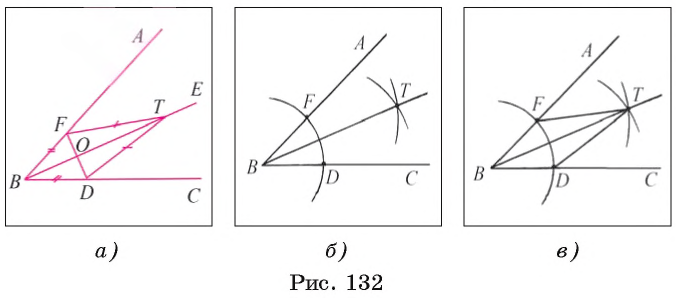
Задача 3 (построение биссектрисы угла)
Постройте биссектрису данного угла ABC.
Поиск решения.
Допустим, что биссектриса BE данного угла ABC построена (рис. 132, а). Пусть точки F и D лежат на сторонах угла так, что BF = BD, О = FD 
Построение.
1) Строим окружность 
2) Отмечаем точки F и D, в которых окружность 
3) Строим окружности 


4) Проводим луч ВТ. Луч ВТ — искомый. Докажем это.
Доказательство.
Рассмотрим треугольники BFT и BDT (рис. 132, в). Эти треугольники равны по трем сторонам (BF = BD и FT = DT — по построению, ВТ — общая сторона). Из равенства этих треугольников следует, что 

Построение треугольника по трем элементам
В данном пункте рассмотрим задачи на построение треугольника по: а) двум сторонам, и углу между ними; б) стороне и двум прилежащим к ней углам; в) трем сторонам.
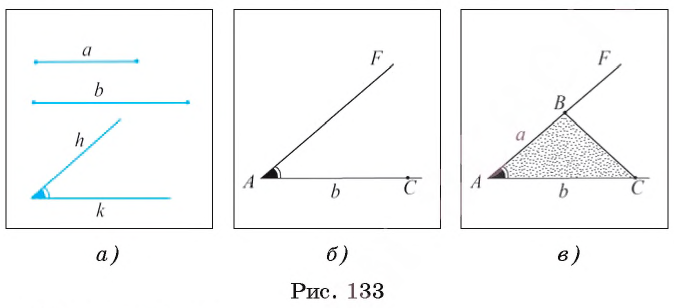
Задача 4 (построение треугольника по двум сторонам и углу между ними)
Постройте треугольник, две стороны которого равны двум данным отрезкам а и b, а угол между этими сторонами равен данному углу hk.
Даны два отрезка а, b и угол hk (рис. 133, а). Требуется с помощью циркуля и линейки построить треугольник ABC, две стороны которого, например, АВ и АС, равны соответственно отрезкам а и b, а угол ВАС равен углу hk.
Построение.
1) Проведем прямую, на ней отложим отрезок АС, равный отрезку b (рис. 133, б).
2) Строим угол CAF, равный углу hk.
3) На луче AF отложим отрезок АВ, равный отрезку а, и проведем отрезок ВС. Треугольник ABC — искомый (рис. 133, в).
Доказательство.
По построению имеем, что АС = b, АВ = а и 

Исследование.
При любых данных отрезках а и b и неразвернутом угле hk каждое из построений 1) — 3) выполнимо, т. е. искомый треугольник можно построить. Треугольники, которые удовлетворяют условию задачи и строятся при различном выборе прямой и отрезка АС, равны между собой по двум сторонам и углу между ними, поэтому говорят, что данная за дача имеет единственное решение.
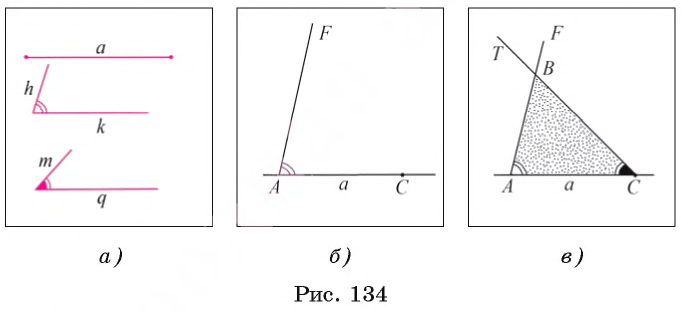
Задача 5 (построение треугольника по стороне и двум прилежащим к ней углам)
Постройте треугольник, сторона которого равна данному отрезку а, а углы, прилежащие к этой стороне, равны данным углам hk и mq.
Дан отрезок а и два угла hk и mq (рис. 134, а). Требуется с помощью циркуля и линейки построить треугольник ABC, сторона которого, например АС, равна отрезку а, а углы ВАС и ВСА равны соответственно углам hk и mq.
Построение.
1) Проведем прямую и на ней отложим с помощью циркуля отрезок АС, равный отрезку а (рис. 134, б).
2) Строим угол CAF, равный углу hk.
3) Строим угол ACT, равный углу mq.
4) Отмечаем точку В пересечения лучей AF и СТ. Треугольник ABC — искомый (рис. 134, в).
Доказательство.
По построению имеем, что АС = a, 



Исследование.
Для любого данного отрезка а и неразвернутых углов hk и mq каждое из построений 1) — 4) выполнимо, т. е. искомый треугольник можно построить. Треугольники, которые удовлетворяют условию задачи и строятся при различном выборе прямой и отрезка АС, равны между собой по стороне и двум прилежащим к ней углам, поэтому говорят, что данная задача имеет единственное решение.
Задача 6 (построение треугольника по трем сторонам)
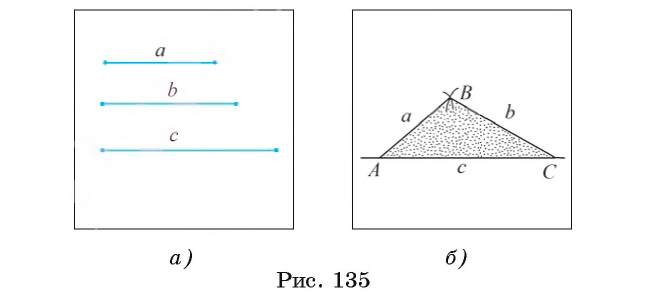
Постройте треугольник, стороны которого равны данным отрезкам а, b, с.
Даны отрезки а, b, с (рис. 135, а). Требуется с помощью циркуля и линейки построить треугольник ABC, стороны которого АВ, ВС и АС равны соответственно отрезкам a, b и с.
Построение.
1) Проведем прямую и на ней с помощью циркуля отложим отрезок АС, равный отрезку с (рис. 135, б).
2) Строим окружность 
3) Строим окружность 
4) Пусть В — одна из точек пересечения окружностей 

Доказательство.
По построению АС = с, АВ = а, ВС = b.
Исследование.
Данная задача не всегда имеет решение. Известно, что в любом треугольнике длина каждой стороны меньше суммы длин двух других его сторон. Таким образом, если длина какого-либо из данных отрезков больше суммы длин двух других, то нельзя построить треугольник, стороны которого равны данным отрезкам.
- Задачи на построение по геометрии
- Угол — определение, виды, как обозначают с примерами
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Соотношения между сторонами и углами треугольника
- Неравенство треугольника — определение и вычисление
- Свойства прямоугольного треугольника
- Расстояние между параллельными прямыми