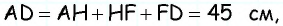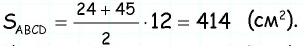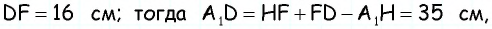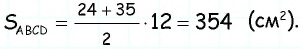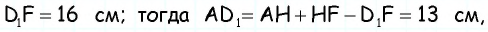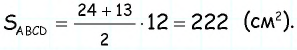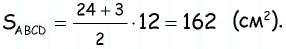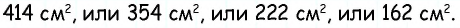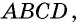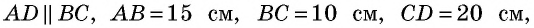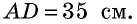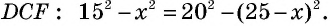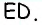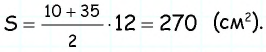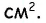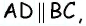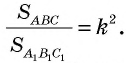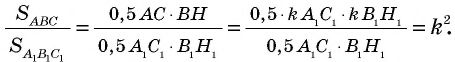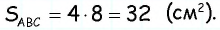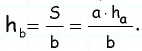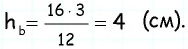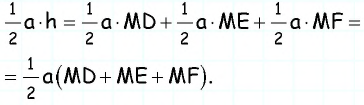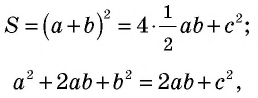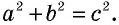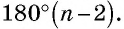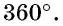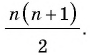Задачи на площадь четырехугольников на три уровня
тренажёр по геометрии (8 класс) на тему
Задачи на нахождение площади четырехугольников на 3 уровня
Скачать:
| Вложение | Размер |
|---|---|
| zadachi_na_ploshchad_po_urovnyam.docx | 15.04 КБ |
Бесплатный марафон подготовки к ЕГЭ на зимних каникулах
Учи.Дома запускает бесплатный марафон в котором каждый день. В течении 5 дней утром ты будешь получать одно задание по выбранному предмету, а вечером его решение. Твоя задача, успеть выполнение задание до того как получишь ответ.
Бесплатно, онлайн, подготовка к ЕГЭ
Предварительный просмотр:
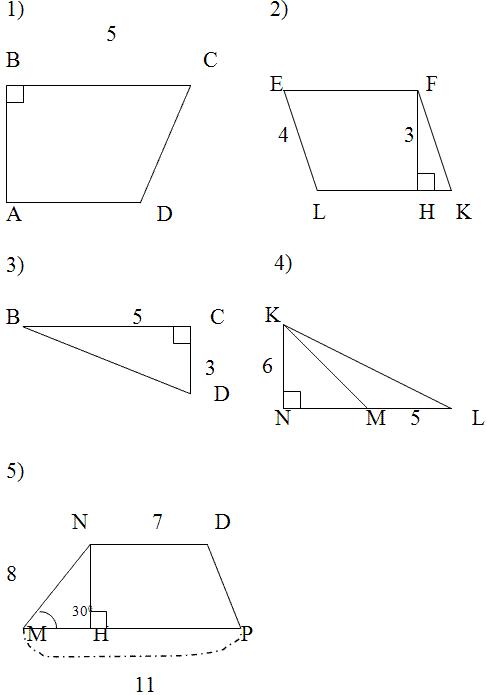
Задачи 1 уровня
1.Найдите площадь прямоугольника, если его длина 2 дм, а ширина 4 см.
2.Найдите площадь параллелограмма, если одна из его сторон равна 6 см , а высота, проведенная к этой стороне, равна 9 см.
3.Катеты прямоугольного треугольника 12 и 8см. Найдите площадь треугольника.
4.Найдите площадь прямоугольника, если его длина 110 см, а ширина 10 м.
5.Найдите площадь прямоугольной трапеции, если основания равны 8 см и 10 см, а боковая сторона, перпендикулярная нижнему основанию равно 5 см.
6.Найдите площадь прямоугольника, если его длина 15 дм, а ширина 20 м.
7.Основания трапеции 6см и 8 см, высота 2 см. Найдите площадь трапеции.
8.Основания трапеции 9 см и 1 см, высота 4 см. Найдите площадь трапеции.
9.Основание треугольника 16, а высота, проведенная к основанию 5. Найдите площадь треугольника.
10.Основание параллелограмма равно 20, а высота, проведенная к основанию равна 7. Найдите площадь параллелограмма.
Задачи 2 уровня.
1.Стороны параллелограмма равны 6 см и 10 см и угол между ними 150 градусов. Найдите площадь параллелограмма.
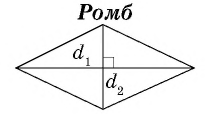
2.Найдите площадь ромба с диагоналями 5см и 8 см.
3.Стороны параллелограмма равны 10 см и 18 см и угол между ними 150 градусов. Найдите площадь параллелограмма.
4.Периметр квадрата 40 см. Найдите его площадь.
5.Площадь квадрата 81 кв. см. Найдите его периметр.
6.Найдите площадь прямоугольного треугольника, если его катеты 8 см и 15 см.
7.Основание равнобедренного треугольника 16 см, а медиана, проведенная к основанию, равна 6 см. Найдите площадь треугольника.
8.Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.
Задачи 3 уровня.
1.Стороны параллелограмма равны 6 см и 10 см и угол между ними 150 градусов. Найдите площадь параллелограмма.
2.Высоты параллелограмма равны 3 см и 4 см, острый угол между сторонами равен 30 градусов. Найдите площадь параллелограмма.
3.Найдите площадь трапеции со сторонами 6 см, 6 см, 10см и 14 см, если угол между боковой стороной и нижнем основанием 30 градусов.
4.Стороны параллелограмма равны 8 см и 15 см и угол между ними 150 градусов. Найдите площадь параллелограмма.
5.Найдите высоту прямоугольного треугольника, проведённую к гипотенузе, если его катеты 8 см и 6 см., а гипотенуза равна 10 см
По теме: методические разработки, презентации и конспекты
Площади четырехугольников
Материал для обобщающего урока по теме «Площади четырехугольников» для 8 класса, представляющий различные формы работы с обучающимися.
Зачет по геометрии в 8 классе по теме «Площади четырехугольников»
Карточка для зачета , 2 варианта.
Разработка урока-соревнования в 8 классе по геометрии на тему «Четырехугольники. Свойства, признаки и площади четырехугольников»
Материал урока систематизирует и обобщает знания о четырехугольниках, их свойствах, признаках, площадях.
Презентация. Решение задач на вычисление площадей четырехугольников.
Данная презентация содержит задачи на вычисление площадей многоугольников: прямоугольника, параллелограмма, а также треугольника, трапеции с применением свойств площадей многоугольников, свойств.
Учебный элемент к уроку геометрии по теме: «Четырехугольники. Формулы для нахождения площадей четырехугольников «
Учебный элемент содержит теоретический материал по данной теме и примеры задач.
Урок геометрии в 8 классе «Решение задач на вычисление площади четырехугольников»
Урок обобщения по теме «Площадь четырехуголников».
Урок по теме «Решение задач на вычисление площади четырехугольников»
Разделы: Математика
Урок рассчитан на один академический час и проводится после того, как изучены формулы для вычисления площадей треугольников, прямоугольника, квадрата, параллелограмма и трапеции.
- Образовательные: повторить ранее изученные формулы для вычисления площадей выпуклых фигур, вывести и научиться пользоваться формулами для вычисления площадей выпуклых четырехугольников, имеющих перпендикулярные диагонали;
- Развивающие: развитие логического мышления, памяти, внимания, выработка математической зоркости;
- Воспитательные: воспитание трудолюбия, интереса к предмету, умение внимательно выслушивать ответы одноклассников.
- Организационный момент.
- Устная работа.
Проводится по чертежам, выведенным с проектора на экран.
Задание. Для каждой из геометрических фигур найти площадь, назвав используемую формулу. Опрос ведется фронтально, учащиеся могут отвечать по желанию.
Учитель обращает внимание учащихся на то, что до сих пор, в основном, площади фигур вычислялись по двум элементам: основанию и высоте, проведенной к основанию. Однако, в случае, если в четырехугольнике диагонали взаимно перпендикулярны, его площадь можно вычислить, зная длины диагоналей.
Учитель просит учащихся сформулировать тему урока. Учащиеся предлагают свои варианты темы урока. Принимается такая: «Вычисление площади выпуклого четырехугольника, имеющего взаимно перпендикулярные диагонали».
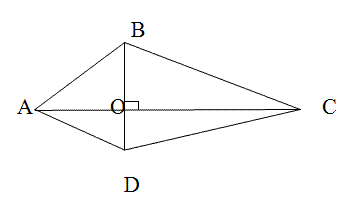
Задача. Доказать, что площадь выпуклого четырехугольника, имеющего взаимно перпендикулярные диагонали, равна половине произведения его диагоналей.
Запись на доске.
ABCD – вып. четырехугольник,
SABCD=1/2 ACBD.
SABC=1/2 ACBО, т.к. BO является высотой в ABC,
SABC=1/2 ACDO, т.к. DO является высотой в ADC.
- SABCD= SABC+ SADC = 1/2 ACBО + 1/2 ACDO = 1/2 AC(BO+DO)= 1/2 ACBD, ч.т.д.
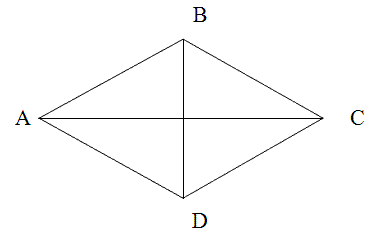
Учитель. Какие вы знаете четырехугольники с взаимно-перпендикулярными диагоналями?
Ученик. Ромб и квадрат.
Учитель. Давайте запишем формулы в общем виде для вычисления площадей ромба и квадрата для их диагоналей.
Запись на доске:
Учитель. Что можно сказать о диагоналях квадрата, кроме того, что они взаимно перпендикулярны?
Ученик. Диагонали квадрата равны, то есть d1 = d2.
Учитель просит ученика записать формулу для вычисления площади квадрата по его диагонали.
Ученик пишет на доске:
Sквадрата = ½ d 2 , где d – диагональ квадрата.
Учитель. Приведите свои примеры использования выведенных формул.
Ученик. Найти площадь ромба, если его диагонали равны 3см и 6см.
Решение: S=1/2 36 = 9 (см 2 ).
Ученик. Найти площадь квадратного участка земли, если его диагональ равна 10м.
Решение: S=1/2 10 2 =50 (м 2 ).
Учитель. Придумайте обратные задачи.
Ученик. Найти одну из диагоналей ромба, если его площадь равна 20 см 2 , а вторая диагональ 8 см.
Решение: d1= 2S/d2, d1= 220/8 = 5 (см)
Ученик. Найти диагональ квадрата, если его площадь равна 18 см 2 .
Решение: d 2 =2S, d 2 =36, d=6(см).
Учитель. Давайте теперь решим более сложную задачу, в которой известны площадь ромба, а также соотношение между длинами диагоналей, а требуется найти диагонали.
(На эту задачу лучше вызвать сильного ученика, т.к. она решается с помощью уравнения и является сложной для слабых учеников). Во время обдумывания решения предложенной задачи средними и сильными учениками класса, слабые получают карточки-задания на отработку выведенных формул. Каждая карточка содержит по 2 простые задачи типа:
Вычислить площадь ромба, если одна из его диагоналей равна 5 см, а другая в 4 раза больше.
Вычислить диагональ квадрата, если его площадь равна 32 см 2 .
Задача (для средних и сильных учеников).
Одна из диагоналей ромба, площадь которого равна 27 см 2 , в 1,5 раза больше другой диагонали. Найти диагонали этого ромба.
Ученик записывает на доске:
- SABCD = 1/2 ACBD.
Пусть BD = x см, тогда AC = 1,5x см. Т.к. по условию задачи SABCD = 27 см 2 , то получаем уравнение:
1/21,5xx = 27,
x=6 ( x=-6 не подходит по смыслу задачи).
- BD = 6 см, AC = 1,56= 9 см.
Ответ : 6 см и 9 см.
Учитель. Какие новые формулы мы сегодня узнали?
Ученик. Формулы для вычисления площадей выпуклых четырехугольников, имеющих взаимно-перпендикулярные диагонали, в частности, для ромба и квадрата.
Учитель. Какая еще из известных вам геометрических фигур может иметь взаимно-перпендикулярные диагонали?
Учитель. Верно, значит можно вычислить и площадь трапеции, если у нее взаимно-перпендикулярные диагонали. Этими формулами можно пользоваться наряду с ранее изученными.
- Домашнее задание (творческое).
- Придумать по 2 задачи (2 прямые и 2 обратные) на применение изученных формул и записать их с решениями. Чем сложнее задача, тем выше оценка.
- Для слабых учеников (у кого не получится придумать задачи):
Задача. Найти площадь трапеции, если ее диагонали взаимно перпендикулярны, а их длины равны 10 см и 16 см.
Решение задач на вычисление площадей с примерами вычисления и определения
Решение задач на вычисление площадей многоугольников чаще всего сводится к поиску величин отдельных элементов рассматриваемых фигур и дальнейшему применению соответствующих формул площадей.
Во многих задачах наряду с сугубо геометрическими приемами решения (дополнительные построения, применение равенства фигур и т. п.) используются и методы алгебры (составление уравнений или систем уравнений на основе метрических соотношений между элементами фигуры).
В ходе решения особое внимание следует уделить тому, однозначно ли данные задачи определяют взаимное расположение элементов фигуры.
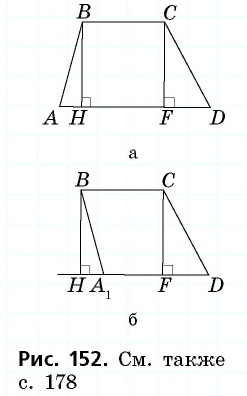
Пример:
Найдите площадь трапеции, в которой одно из оснований равно 24 см, высота 12 см, а боковые стороны — 13 см и 20 см.
Решение:
Пусть
1) Для трапеции (рис. 152, а): из треугольника по теореме Пифагора имеем аналогично из треугольника имеем тогда
2) Для трапеции (рис. 152, б): из треугольника по теореме Пифагора имеем аналогично из треугольника имеем
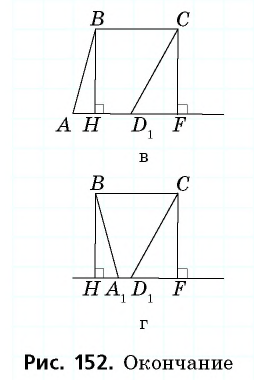
3) Для трапеции (рис. 152, в): из треугольника по теореме Пифагора имеем аналогично из треугольника имеем
4) Для трапеции (рис. 152, г): из треугольника по теореме Пифагора имеем аналогично из треугольника имеем тогда т.е. точки расположены на прямой в указанном порядке.
Ответ:
Рассмотренная задача наглядно демонстрирует одну из причин, по которым в процессе решения геометрической задачи может возникать многовариантность. Но даже если такая ситуация не возникает, взаимное расположение элементов фигур нуждается в обосновании.
Пример:
Основания трапеции равны 10 см и 35 см, а боковые стороны — 15 см и 20 см. Найдите площадь трапеции.
Прежде всего заметим, что решение данной задачи фактически сводится к нахождению высоты трапеции. Итак, пусть дана трапеция
Естественно было бы провести, как в предыдущей задаче, высоты (рис. 153) и составить уравнение на основании теоремы Пифагора, примененной к треугольникам и
Такое решение позволит получить правильный ответ, но не будет полным, ведь принадлежность точек отрезку нужно обосновать. Попробуем избежать необходимости такого обоснования, применив для решения другое дополнительное построение.
Решение:
Проведем через вершину прямую параллельную (рис. 154).
Поскольку по построению — параллелограмм, то следовательно, Стороны треугольника пропорциональны числам 3, 4, 5, следовательно, по теореме, обратной теореме Пифагора, он является прямоугольным с гипотенузой
По формуле находим высоту этого треугольника, которая одновременно является и высотой трапеции: Следовательно,
Ответ: 270
Как видим, этот способ намного более рационален, в частности, с точки зрения вычислений. Рассмотрим еще одну задачу, для решения которой используется дополнительное построение.
Пример:
Диагонали трапеции равны 30 см и 40 см и пересекаются под прямым углом. Найдите площадь трапеции.
Попробуем решить эту задачу чисто геометрическими методами. Основная сложность заключается в том, что данные отрезки не являются сторонами одного треугольника. Попробуем «исправить» эту ситуацию.
Решение:
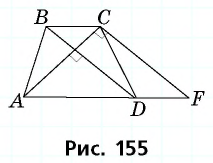
Пусть дана трапеция в которой Проведем через вершину прямую параллельную диагонали (рис. 155).
Очевидно, что по построению угол будет прямым, т.е. треугольник прямоугольный с гипотенузой С другой стороны, — параллелограмм, тогда
Обратим внимание на то, что треугольники равновеликие, поскольку а высоты, проведенные к этим сторонам, являются высотами трапеции. Таким образом, т.е. искомая площадь трапеции равна площади треугольника которая, в свою очередь, равна полупроизведению его катетов:
Ответ: 600
Применение площадей
Теорема (об отношении площадей подобных треугольников)
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Пусть с коэффициентом т.е. Докажем, что
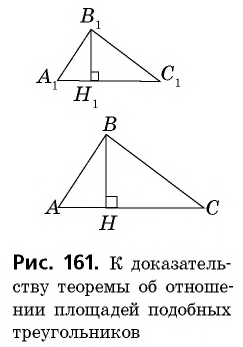
Проведем в данных треугольниках высоты (рис. 161).
Прямоугольные треугольники подобны, поскольку Это означает, что т.е. Учитывая, что имеем:
Пример:
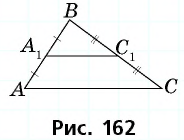
Средняя линия отсекает от данного треугольника треугольник с площадью 8 Найдите площадь данного треугольника.
Решение:
Пусть — средняя линия треугольника параллельная стороне (рис. 162),
Треугольники подобны по двум сторонам и углу между ними, причем Тогда по доказанной теореме откуда
Ответ:
Метод площадей
Понятия площади и формулы ее вычисления могут применяться даже в тех задачах, в условиях которых площадь не упоминается. Рассмотрим такой пример.
Пример:
Стороны параллелограмма равны 16 см и 12 см. Высота параллелограмма, проведенная к большей стороне, равна 3 см. Найдите высоту, проведенную к меньшей стороне.
Решение:
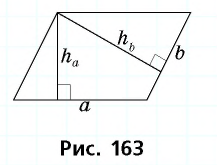
Пусть дан параллелограмм со сторонами к которым проведены высоты длину которой необходимо найти (рис. 163).
По формуле площади параллелограмма откуда
Таким образом,
При решении этой задачи площадь параллелограмма вычислялась двумя разными способами. Поскольку площадь многоугольника независимо от способа ее вычисления определяется однозначно, то полученные выражения приравнивались, благодаря чему удалось связать известные величины с искомой. Такой метод, основанный на использовании площади как вспомогательной величины, называется методом вспомогательной площади или просто методом площадей.
Заметим, что из формул площади параллелограмма и площади треугольника следует важное утверждение: в параллелограмме (треугольнике) большей является высота, проведенная к меньшей стороне, меньшей — высота, проведенная к большей стороне.
Метод площадей используется как в задачах на вычисление, так и для доказательства утверждений.
Пример:
Сумма расстояний от точки, взятой внутри равностороннего треугольника, до его сторон не зависит от выбора точки и равна высоте треугольника. Докажите.
Решение:
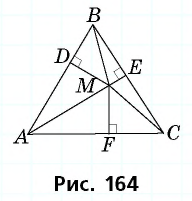
Пусть точка лежит внутри равностороннего треугольника со стороной и — расстояния от данной точки до сторон треугольника (рис. 164).
Соединим точку с вершинами треугольника. Площадь треугольника равна сумме площадей треугольников и в которых отрезки являются высотами. Имеем:
Отсюда т.е. сумма рассматриваемых расстояний равна высоте треугольника и не зависит от выбора точки
Другие доказательства теоремы Пифагора
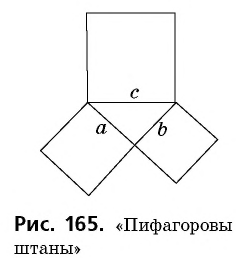
Исторически появление и доказательство теоремы Пифагора связаны с вычислением площадей. Поэтому в классической формулировке этой теоремы речь идет не о квадратах сторон прямоугольного треугольника, а о площадях соответствующих фигур:
- площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
Рисунок 165, который наглядно воплощает эту формулировку, стал своеобразным символом геометрии и среди гимназистов позапрошлого столетия получил название «пифагоровы штаны».
Шутливый стишок про «пифагоровы штаны» школьники запоминали на всю жизнь.
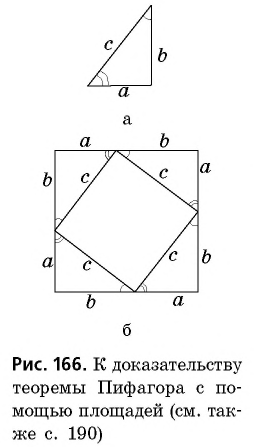
Докажем теорему Пифагора с помощью площадей.
Пусть дан прямоугольный треугольник с катетами и гипотенузой (рис. 166, а). Достроим его до квадрата со стороной так, как показано на рисунке 166, б. Площадь этого квадрата равна Построенный квадрат состоит из четырех равных прямоугольных треугольников площадью и четырехугольника со сторонами длиной который является квадратом (докажите это самостоятельно). Итак, имеем: ^
т.е.
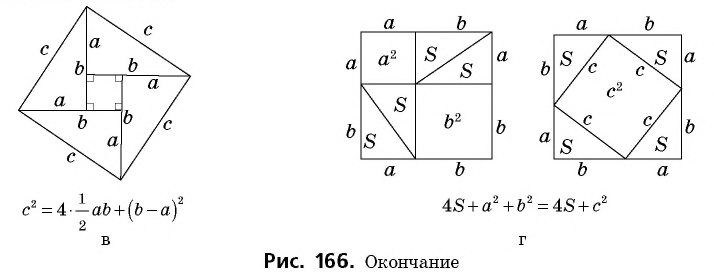
На рисунках 166, в, г показаны другие способы доказательства теоремы Пифагора с помощью площадей. В трактатах индийского математика XII ст. Бхаскари один из них сопровождался только одним словом: «Смотри!». В целом сегодня известно более 150 разных способов доказательства этой знаменитой теоремы. Но каждый из вас может изобрести и свой собственный способ.
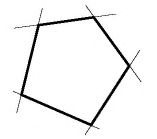
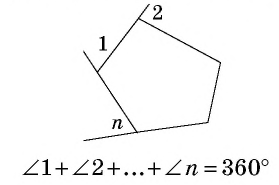
Многоугольник называется выпуклым, если он лежит по одну сторону от любой прямой, содержащей его сторону
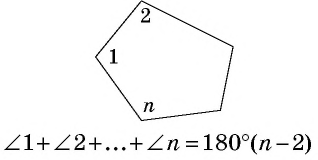
Сумма углов многоугольника
Сумма углов выпуклого -угольника равна
Сумма внешних углов выпуклого -угольника, взятых по одному при каждой вершине, равна
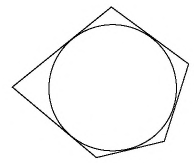
Описанный многоугольник
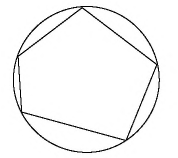
Многоугольник называется вписанным в окружность, если все его вершины лежат в этой окружности.
Описанный многоугольник.
Многоугольником называют описанным около окружностей, если все его стороны касаются этой окружности.
Аксиомы площадей
- Равные многоугольники имеют равные площади.
- Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
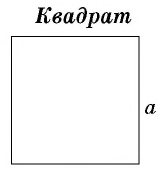
- Площадь квадрата со стороной, равной единице длины, равна единице площади
Две фигуры называются равновеликими, если они имеют равные площади
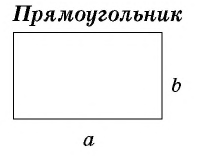
где — стороны прямоугольника.
где — сторона квадрата
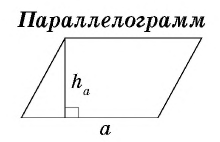
где — сторона параллелограмма,
— проведенная к ней высота
где — сторона треугольника, — проведенная к ней высота.
— катеты прямоугольного треугольника.
где — сторона треугольника.
где — диагонали ромба.
где основание трапеции, — высота трапеции.
Теорема об отношении площадей подобных треугольников Отношение площадей подобных треугольников равно квадрату коэффициента подобия
Историческая справка:
Вычисление площадей многоугольников — первая среди тех практических задач, благодаря которым появилась геометрия как наука. Но не всегда представление об измерении площадей было таким, как сегодня.
Например, древние египтяне при вычислении площади любого треугольника брали половину произведения двух его сторон. Так же пять столетий назад измеряли площадь треугольника и в Древней Руси. Чтобы найти площадь четырехугольника, который не является квадратом, в Вавилоне использовали формулу произведения полусумм его противолежащих сторон.
В Средние века для вычисления площади треугольника со стороной и проведенной к ней высотой, которые выражаются целым числом брали сумму членов натурального ряда от 1 до т.е. число
Кстати, в то время знали и правильную формулу площади этого треугольника Ее обосновал средневековый математик Герберт, который в X ст. даже занимал какое-то время престол Римского Папы под именем Сильвестра II.
Древние вавилоняне еще четыре тысячи лет назад умели правильно вычислять площадь квадрата, прямоугольника, трапеции. Немало формул площадей и объемов, с которыми вы познакомитесь в старших классах, открыл знаменитый греческий ученый Архимед (ок. 287-212 гг. до н. э.). И это все при том, что в те древние времена не было даже алгебраической символики!
Сегодня, благодаря значительно более широкому применению алгебры в геометрии, мы имеем возможность дать куда более простые и понятные решения многих задач, чем это было возможно в те далекие времена.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Тела вращения: цилиндр, конус, шар
- Четырехугольник
- Площади фигур в геометрии
- Площади поверхностей геометрических тел
- Эллипс
- Гипербола
- Парабола
- Многогранник
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://urok.1sept.ru/articles/523943
http://www.evkova.org/reshenie-zadach-na-vyichislenie-ploschadej
Урок рассчитан на один
академический час и проводится после того,
как изучены формулы для вычисления
площадей треугольников, прямоугольника,
квадрата, параллелограмма и трапеции.
Цели урока:
- Образовательные: повторить ранее
изученные формулы для вычисления
площадей выпуклых фигур, вывести и
научиться пользоваться формулами для
вычисления площадей выпуклых
четырехугольников, имеющих
перпендикулярные диагонали; - Развивающие: развитие логического
мышления, памяти, внимания, выработка
математической зоркости; - Воспитательные: воспитание трудолюбия,
интереса к предмету, умение внимательно
выслушивать ответы одноклассников.
Необходимое оборудование:
-
компьютер,
-
проектор.
Ход урока.
- Организационный момент.
- Устная работа.
Проводится по чертежам,
выведенным с проектора на экран.
Задание. Для каждой из
геометрических фигур найти площадь, назвав
используемую формулу. Опрос ведется
фронтально, учащиеся могут отвечать по
желанию.
- Введение новых знаний.
Учитель обращает внимание
учащихся на то, что до сих пор, в основном,
площади фигур вычислялись по двум
элементам: основанию и высоте, проведенной
к основанию. Однако, в случае, если в
четырехугольнике диагонали взаимно
перпендикулярны, его площадь можно
вычислить, зная длины диагоналей.
Учитель просит учащихся
сформулировать тему урока. Учащиеся
предлагают свои варианты темы урока.
Принимается такая: «Вычисление площади
выпуклого четырехугольника, имеющего
взаимно перпендикулярные диагонали».
Задача. Доказать, что площадь
выпуклого четырехугольника, имеющего
взаимно перпендикулярные диагонали, равна
половине произведения его диагоналей.
Запись на доске.
Дано:
ABCD – вып. четырехугольник,
AC ┴ BD.
Доказать:
SABCD=1/2 AC
Доказательство:
- пусть AC ∩ BD = O, тогда
S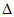
AC
т.к. BO является высотой в 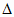
S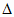
AC
т.к. DO является высотой в
ADC.
- SABCD= S
ABC+
SADC
= 1/2 ACBО
+ 1/2 ACDO
= 1/2 AC(BO+DO)=
1/2 ACBD,
ч.т.д.
Учитель. Какие вы знаете
четырехугольники с взаимно-перпендикулярными
диагоналями?
Ученик. Ромб и квадрат.
Учитель. Давайте запишем
формулы в общем виде для вычисления
площадей ромба и квадрата для их диагоналей.
Запись на доске:
Sромба=1/2d1d2, где
d1, d2 – диагонали ромба.
Учитель. Что можно сказать о
диагоналях квадрата, кроме того, что они
взаимно перпендикулярны?
Ученик. Диагонали квадрата
равны, то есть d1 = d2.
Учитель просит ученика
записать формулу для вычисления площади
квадрата по его диагонали.
Ученик пишет на доске:
Sквадрата =
½ d2, где d – диагональ квадрата.
- Закрепление выведенных формул.
Учитель. Приведите свои
примеры использования выведенных формул.
Ученик. Найти площадь ромба,
если его диагонали равны 3см и 6см.
Решение: S=1/2 

= 9 (см2).
Ученик. Найти площадь
квадратного участка земли, если его
диагональ равна 10м.
Решение: S=1/2 
(м2).
Учитель. Придумайте обратные
задачи.
Ученик. Найти одну из
диагоналей ромба, если его площадь равна 20
см2, а вторая диагональ 8 см.
Решение: d1= 2S/d2, d1= 2
= 5 (см)
Ученик. Найти диагональ
квадрата, если его площадь равна 18 см2.
Решение: d2=2S, d2=36, d=6(см).
Учитель. Давайте теперь решим
более сложную задачу, в которой известны
площадь ромба, а также соотношение между
длинами диагоналей, а требуется найти
диагонали.
(На эту задачу лучше вызвать
сильного ученика, т.к. она решается с
помощью уравнения и является сложной для
слабых учеников). Во время обдумывания
решения предложенной задачи средними и
сильными учениками класса, слабые получают
карточки-задания на отработку выведенных
формул. Каждая карточка содержит по 2
простые задачи типа:
-
Вычислить площадь ромба, если
одна из его диагоналей равна 5 см, а другая
в 4 раза больше. -
Вычислить диагональ квадрата,
если его площадь равна 32 см2.
Задача (для средних и сильных
учеников).
Одна из диагоналей ромба, площадь
которого равна 27 см2, в 1,5 раза больше
другой диагонали. Найти диагонали этого
ромба.
Ученик записывает на доске:
Дано:
ABCD – ромб,
AC = 1,5 BD,
SABCD = 27 см2.
Найти:
AC, BD.
Решение:
- SABCD = 1/2 AC
BD.
Пусть BD = x см, тогда AC = 1,5x см. Т.к.
по условию задачи SABCD = 27 см2, то
получаем уравнение:
1/2

= 27,
1,5x2=54,
x2=36,
x=6 ( x=-6 не подходит по смыслу
задачи).
- BD = 6 см, AC = 1,5
6=
9 см.
Ответ : 6 см и 9 см.
- Итог урока.
Учитель. Какие новые формулы
мы сегодня узнали?
Ученик. Формулы для вычисления
площадей выпуклых четырехугольников,
имеющих взаимно-перпендикулярные
диагонали, в частности, для ромба и квадрата.
Учитель. Какая еще из известных
вам геометрических фигур может иметь
взаимно-перпендикулярные диагонали?
Ученик. Трапеция.
Учитель. Верно, значит можно
вычислить и площадь трапеции, если у нее
взаимно-перпендикулярные диагонали. Этими
формулами можно пользоваться наряду с
ранее изученными.
- Домашнее задание (творческое).
- Придумать по 2 задачи (2 прямые и 2
обратные) на применение изученных формул
и записать их с решениями. Чем сложнее
задача, тем выше оценка. - Для слабых учеников (у кого не получится
придумать задачи):
Задача. Найти площадь трапеции,
если ее диагонали взаимно перпендикулярны,
а их длины равны 10 см и 16 см.
Решение задач на вычисление площадей многоугольников чаще всего сводится к поиску величин отдельных элементов рассматриваемых фигур и дальнейшему применению соответствующих формул площадей.
Во многих задачах наряду с сугубо геометрическими приемами решения (дополнительные построения, применение равенства фигур и т. п.) используются и методы алгебры (составление уравнений или систем уравнений на основе метрических соотношений между элементами фигуры).
В ходе решения особое внимание следует уделить тому, однозначно ли данные задачи определяют взаимное расположение элементов фигуры.
Пример:
Найдите площадь трапеции, в которой одно из оснований равно 24 см, высота 12 см, а боковые стороны — 13 см и 20 см.
Решение:
Пусть
1) Для трапеции 
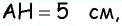
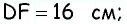
2) Для трапеции 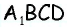
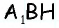
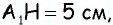
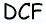
3) Для трапеции 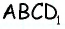
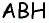
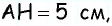
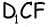
4) Для трапеции 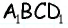
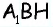
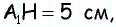
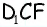
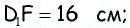
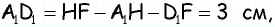
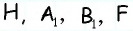
Ответ:
Рассмотренная задача наглядно демонстрирует одну из причин, по которым в процессе решения геометрической задачи может возникать многовариантность. Но даже если такая ситуация не возникает, взаимное расположение элементов фигур нуждается в обосновании.
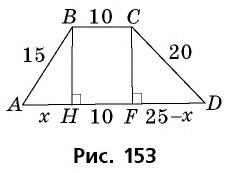
Пример:
Основания трапеции равны 10 см и 35 см, а боковые стороны — 15 см и 20 см. Найдите площадь трапеции.
Прежде всего заметим, что решение данной задачи фактически сводится к нахождению высоты трапеции. Итак, пусть дана трапеция
Естественно было бы провести, как в предыдущей задаче, высоты 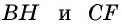
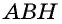
Такое решение позволит получить правильный ответ, но не будет полным, ведь принадлежность точек 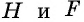
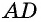
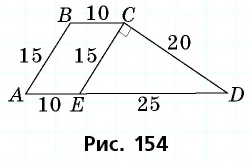
Решение:
Проведем через вершину 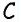
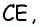

Поскольку по построению 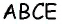
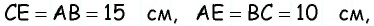
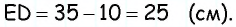
По формуле 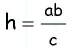
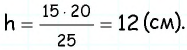
Ответ: 270
Как видим, этот способ намного более рационален, в частности, с точки зрения вычислений. Рассмотрим еще одну задачу, для решения которой используется дополнительное построение.
Пример:
Диагонали трапеции равны 30 см и 40 см и пересекаются под прямым углом. Найдите площадь трапеции.
Попробуем решить эту задачу чисто геометрическими методами. Основная сложность заключается в том, что данные отрезки не являются сторонами одного треугольника. Попробуем «исправить» эту ситуацию.
Решение:
Пусть дана трапеция 
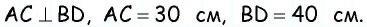
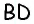
Очевидно, что по построению угол 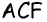
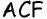
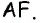
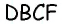
Обратим внимание на то, что треугольники 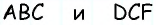
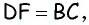
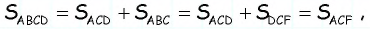

Ответ: 600
Применение площадей
Теорема (об отношении площадей подобных треугольников)
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство:
Пусть 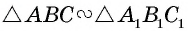
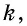
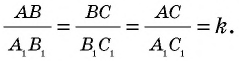
Проведем в данных треугольниках высоты 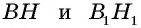
Прямоугольные треугольники 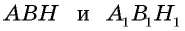
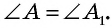
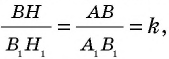
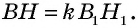
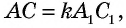
Пример:
Средняя линия отсекает от данного треугольника треугольник с площадью 8 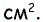
Решение:
Пусть 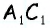
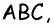

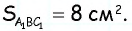
Треугольники 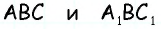
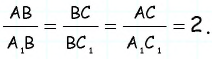
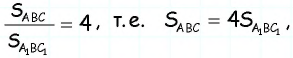
Ответ:
Метод площадей
Понятия площади и формулы ее вычисления могут применяться даже в тех задачах, в условиях которых площадь не упоминается. Рассмотрим такой пример.
Пример:
Стороны параллелограмма равны 16 см и 12 см. Высота параллелограмма, проведенная к большей стороне, равна 3 см. Найдите высоту, проведенную к меньшей стороне.
Решение:
Пусть дан параллелограмм со сторонами 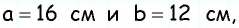

По формуле площади параллелограмма 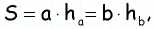
Таким образом,
Ответ: 4 см.
При решении этой задачи площадь параллелограмма вычислялась двумя разными способами. Поскольку площадь многоугольника независимо от способа ее вычисления определяется однозначно, то полученные выражения приравнивались, благодаря чему удалось связать известные величины с искомой. Такой метод, основанный на использовании площади как вспомогательной величины, называется методом вспомогательной площади или просто методом площадей.
Заметим, что из формул площади параллелограмма 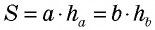
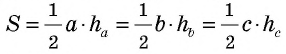
Метод площадей используется как в задачах на вычисление, так и для доказательства утверждений.
Пример:
Сумма расстояний от точки, взятой внутри равностороннего треугольника, до его сторон не зависит от выбора точки и равна высоте треугольника. Докажите.
Решение:
Пусть точка 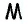
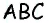
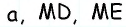
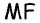
Соединим точку 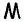
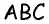
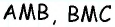
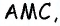
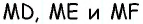
Отсюда 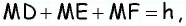
Другие доказательства теоремы Пифагора
Исторически появление и доказательство теоремы Пифагора связаны с вычислением площадей. Поэтому в классической формулировке этой теоремы речь идет не о квадратах сторон прямоугольного треугольника, а о площадях соответствующих фигур:
- площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
Рисунок 165, который наглядно воплощает эту формулировку, стал своеобразным символом геометрии и среди гимназистов позапрошлого столетия получил название «пифагоровы штаны».
Шутливый стишок про «пифагоровы штаны» школьники запоминали на всю жизнь.
Докажем теорему Пифагора с помощью площадей.
Доказательство:
Пусть дан прямоугольный треугольник с катетами 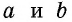
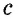
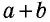
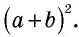
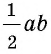
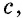
т.е.
Теорема доказана.
На рисунках 166, в, г показаны другие способы доказательства теоремы Пифагора с помощью площадей. В трактатах индийского математика XII ст. Бхаскари один из них сопровождался только одним словом: «Смотри!». В целом сегодня известно более 150 разных способов доказательства этой знаменитой теоремы. Но каждый из вас может изобрести и свой собственный способ.
Итоги главы 3.
Многоугольник называется выпуклым, если он лежит по одну сторону от любой прямой, содержащей его сторону
Сумма углов многоугольника
Сумма углов выпуклого 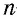
Сумма внешних углов выпуклого 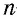
Описанный многоугольник
Многоугольник называется вписанным в окружность, если все его вершины лежат в этой окружности.
Описанный многоугольник.
Многоугольником называют описанным около окружностей, если все его стороны касаются этой окружности.
Аксиомы площадей
- Равные многоугольники имеют равные площади.
- Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
- Площадь квадрата со стороной, равной единице длины, равна единице площади
Две фигуры называются равновеликими, если они имеют равные площади
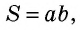
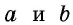
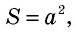
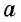
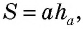
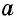
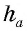
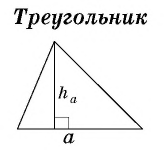
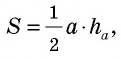
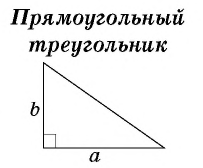
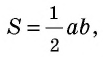
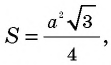
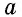
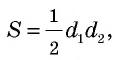
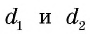
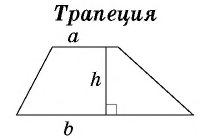
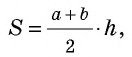
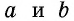
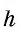
Теорема об отношении площадей подобных треугольников Отношение площадей подобных треугольников равно квадрату коэффициента подобия
Историческая справка:
Вычисление площадей многоугольников — первая среди тех практических задач, благодаря которым появилась геометрия как наука. Но не всегда представление об измерении площадей было таким, как сегодня.
Например, древние египтяне при вычислении площади любого треугольника брали половину произведения двух его сторон. Так же пять столетий назад измеряли площадь треугольника и в Древней Руси. Чтобы найти площадь четырехугольника, который не является квадратом, в Вавилоне использовали формулу произведения полусумм его противолежащих сторон.
В Средние века для вычисления площади треугольника со стороной и проведенной к ней высотой, которые выражаются целым числом 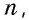
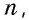
Кстати, в то время знали и правильную формулу площади этого треугольника 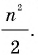
Древние вавилоняне еще четыре тысячи лет назад умели правильно вычислять площадь квадрата, прямоугольника, трапеции. Немало формул площадей и объемов, с которыми вы познакомитесь в старших классах, открыл знаменитый греческий ученый Архимед (ок. 287-212 гг. до н. э.). И это все при том, что в те древние времена не было даже алгебраической символики!
Сегодня, благодаря значительно более широкому применению алгебры в геометрии, мы имеем возможность дать куда более простые и понятные решения многих задач, чем это было возможно в те далекие времена.
- Тела вращения: цилиндр, конус, шар
- Четырехугольник
- Площади фигур в геометрии
- Площади поверхностей геометрических тел
- Эллипс
- Гипербола
- Парабола
- Многогранник
Задачи 1 уровня
1.Найдите площадь прямоугольника, если его длина 2 дм, а ширина 4 см.
2.Найдите площадь параллелограмма, если одна из его сторон равна 6 см, а высота, проведенная к этой стороне, равна 9 см.
3.Катеты прямоугольного треугольника 12 и 8см. Найдите площадь треугольника.
4.Найдите площадь прямоугольника, если его длина 110 см, а ширина 10 м.
5.Найдите площадь прямоугольной трапеции, если основания равны 8 см и 10 см, а боковая сторона, перпендикулярная нижнему основанию равно 5 см.
6.Найдите площадь прямоугольника, если его длина 15 дм, а ширина 20 м.
7.Основания трапеции 6см и 8 см, высота 2 см. Найдите площадь трапеции.
8.Основания трапеции 9 см и 1 см, высота 4 см. Найдите площадь трапеции.
9.Основание треугольника 16, а высота, проведенная к основанию 5. Найдите площадь треугольника.
10.Основание параллелограмма равно 20, а высота, проведенная к основанию равна 7. Найдите площадь параллелограмма.
_______________________________________________________________________________________
Задачи 2 уровня.
1.Стороны параллелограмма равны 6 см и 10 см и угол между ними 150 градусов. Найдите площадь параллелограмма.
2.Найдите площадь ромба с диагоналями 5см и 8 см.
3.Стороны параллелограмма равны 10 см и 18 см и угол между ними 150 градусов. Найдите площадь параллелограмма.
4.Периметр квадрата 40 см. Найдите его площадь.
5.Площадь квадрата 81 кв. см. Найдите его периметр.
6.Найдите площадь прямоугольного треугольника, если его катеты 8 см и 15 см.
7.Основание равнобедренного треугольника 16 см, а медиана, проведенная к основанию, равна 6 см. Найдите площадь треугольника.
8.Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.
_____________________________________________________________________________________
Задачи 3 уровня.
1.Стороны параллелограмма равны 6 см и 10 см и угол между ними 150 градусов. Найдите площадь параллелограмма.
2.Высоты параллелограмма равны 3 см и 4 см, острый угол между сторонами равен 30 градусов. Найдите площадь параллелограмма.
3.Найдите площадь трапеции со сторонами 6 см, 6 см, 10см и 14 см, если угол между боковой стороной и нижнем основанием 30 градусов.
4.Стороны параллелограмма равны 8 см и 15 см и угол между ними 150 градусов. Найдите площадь параллелограмма.
5.Найдите высоту прямоугольного треугольника, проведённую к гипотенузе, если его катеты 8 см и 6 см., а гипотенуза равна 10 см
Скачать материал
Выберите документ из архива для просмотра:
раздаточный материал.docx
решение задач на площади.pptx
Выбранный для просмотра документ раздаточный материал.docx
Скачать материал


- Сейчас обучается 139 человек из 50 регионов


- Сейчас обучается 35 человек из 26 регионов


- Сейчас обучается 49 человек из 26 регионов


Выбранный для просмотра документ решение задач на площади.pptx

Скачать материал
Описание презентации по отдельным слайдам:
-
1 слайд
Решение задач на вычисление площади фигур
Презентация к уроку геометрии 8 класса
Учителя математики Кзыл-Агашской ООШ
Хусаиновой Р.Ш. -
2 слайд
Цель урока:
отработать применение формулы площадей многоугольников при решении задач; совершенствовать навыки решения задач и умения распознавать необходимой формулы -
3 слайд
Цитата к уроку
Умение решать задачи — такое же практическое искусство, как умение плавать или бегать на лыжах. Ему можно научиться только путём подражания или упражнения.
Д. Пойа -
4 слайд
Определение темы и задач урока
Исходя из цитаты урока, определите тему и задачи урока.
Мы с вами изучили формулы площадей четырехугольников. Вы должны знать эти формулы и различать их. Поэтому в первую очередь хочу дать вам тест на распознавание формул и соответствующей фигуры.
(раздать листочки с тестами) -
5 слайд
1.Установите соответствие между фигурами и формулой его площади
а) трапеция
Б) треугольник
В) квадрат
Г) ромб
Д) прямоугольник
Е) прямоугольный треугольник
Ж) параллелограмм -
6 слайд
тест
2. Формулы какой фигуры нет в тесте?
Напишите в тетради формулу площади и рядом название фигуры(собрать листы с тестом)
-
7 слайд
Проверка теста
а) трапеция
Б) треугольник
В) квадрат
Г) ромб
Д) прямоугольник
Е) прямоугольный треугольник
Ж) параллелограмм -
8 слайд
Проверка теста
2. нет формулы параллелограмма
S=a*h -
9 слайд
/
Ответ: 24 кв.см -
-
11 слайд
Решение задач (ОГЭ)
Ответ______15____
-
12 слайд
Решение задач (ОГЭ)
ОТВЕТ___15_____ -
13 слайд
РЕШЕНИЕ ЗАДАЧ
Найдите площадь ромба, если его диагонали равны 19 и 6.
Два катета прямоугольного треугольника равны 4 и 11. Найдите площадь этого треугольника.
Сторона треугольника равна 29, а высота, проведённая к этой стороне, равна 12. Найдите площадь этого треугольника. -
14 слайд
1 группа.
1. Стороны параллелограмма равны 6 и 8 см, а угол между ними равен 300. Найти площадь параллелограмма.
2. В равнобедренной трапеции АВСМ большее основание АМ равно 20см, высота ВН отсекает от АМ отрезок АН, равный 6см. Угол ВАМ равен 450. Найти площадь трапеции. -
15 слайд
2 группа.
1. В равнобедренном треугольнике АВС высота ВН равна 12см, а основание АС в 3 раза больше высоты ВН. Найти площадь треугольника.
2. В параллелограмме АВСД стороны равны 14 и 8 см, высота, проведенная к большей стороне, равна 4см. Найти площадь параллелограмма и вторую высоту. -
16 слайд
ИТОГИ УРОКА
РЕФЛЕКСИЯ
Оцените свою работу в группе. Кто лучше работал? Какую оценку вы поставите?Домашнее задание:
-
17 слайд
В прямоугольном треугольнике один из катетов
равен 10, а угол, лежащий напротив него,
равен 450 . Найдите площадь треугольника.
А
В
С
S-?
10
450 -
18 слайд
Одна из сторон параллелограмма равна 12,
другая равна 5, а один из углов — 300.
Найдите площадь параллелограмма.
А
В
С
D
Подсказка (3):
30
12
5
300.
S-?
Н
АН=2,5
Краткое описание документа:
Урок геометрии в 8 классе на тему «Решение задач на нахождение площадей изученных четырехугольников». В начале урока предъявляется тест на знание формул площадей четырехугольников и треугольников. Решаются задачи по готовым чертежам по теме. К концу урока учащиеся в группе решают задачи на применение формул площадей и работы проверяются экспертами (жюри)
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 268 547 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
Другие материалы
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Маркетинг: теория и методика обучения в образовательной организации»
-
Курс повышения квалификации «Основы управления проектами в условиях реализации ФГОС»
-
Курс повышения квалификации «Введение в сетевые технологии»
-
Курс повышения квалификации «Разработка бизнес-плана и анализ инвестиционных проектов»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс повышения квалификации «Методы и инструменты современного моделирования»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
-
Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»