Содержание:
- Определение и формула силы Ампера
- Закон Ампера
- Силы, действующие на проводники с током в магнитном поле
- Единицы измерения силы Ампера
- Примеры решения задач
Определение и формула силы Ампера
Определение
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Ее обозначения:
$bar{F}, bar{F}_A$ . Сила Ампера векторная величина. Ее направление определяет
правило левой руки: следует расположить ладонь левой руки так, чтобы силовые линии магнитного поля входили в нее.
Вытянутые четыре пальца указывали направление силы тока. В таком случае отогнутый на
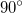
Закон Ампера
Элементарная сила Ампера
($dbar{F}_A$) определена законом (или формулой) Ампера:
$$d bar{F}_{A}=I d bar{l} times bar{B}(1)$$
где I – сила тока,
$d bar{l}$ – малый элемент длины проводника – это вектор, равный
по модулю длине проводника, направленный в таком же направлении как вектор плотности тока,
$bar{B}$ – индукция магнитного поля, в которое помещен проводник с током.
Иначе эту формулу для силы Ампера записывают как:
$$d bar{F}_{A}=bar{j} times bar{B} d V(2)$$
где $bar{j}$ – вектор плотности тока, dV – элемент объема проводника.
Модуль силы Ампера находят в соответствии с выражением:
$$d F=I cdot B cdot d l cdot sin alpha(3)$$
где $alpha$ – угол между векторами магнитной индукции и направление течения тока. Из выражения (3) очевидно, что
сила Ампера максимальна в случае перпендикулярности линий магнитной индукции поля по отношению к проводнику с током.
Силы, действующие на проводники с током в магнитном поле
Из закона Ампера следует, что на проводник с током, равным I, действует сила равная:
$$bar{F}_{A}=I int_{l} d bar{l} times bar{B}(4)$$
где $bar{B}$ магнитная индукция, рассматриваемая в пределах малого кусочка проводника dl.
Интегрирование в формуле (4) проводят по всей длине проводника (l). Из выражения (4) следует, что на замкнутый контур с током I,
в однородном магнитном поле действует сила Ампера равная $bar{F}_{A}=0(H)$
Сила Ампера, которая действует на элемент (dl) прямого проводника с током I1, помещённый в магнитное поле, которое
создает другой прямой проводник, параллельный первому с током I2, равна по модулю:
$$d F=frac{mu_{0}}{2 pi} frac{I_{1} I_{2}}{d} d l(5)$$
где d – расстояние между проводниками, $mu_{0}=4 pi cdot 10^{7}$ Гн/м(или Н/А2 ) – магнитная постоянная.
Проводники с токами одного направления притягиваются. Если направления токов в проводниках различны, то они отталкиваются.
Для рассмотренных выше параллельных проводников бесконечной длины сила Амперана единицу длины может быть вычислена по формуле:
$$frac{F}{l}=frac{mu_{0}}{2 pi} frac{I_{1} I_{2}}{d}$$
Формулу (6) в системе СИ применяют для получения количественного значения магнитной постоянной.
Единицы измерения силы Ампера
Основной единицей измерения силы Ампер (как и любой другой силы) в системе СИ является: [FA]=H
В СГС: [FA]=дин
Примеры решения задач
Пример
Задание. Прямой проводник длины l с током I находится в однородном магнитном поле B. На проводник
действует сила F. Каков угол между направлением течения тока и вектором магнитной индукции?
Решение. На проводник с током, находящийся в магнитном поле действует сила Ампера, модуль которой для
прямолинейного проводника с током расположенном в однородном поле можно представить как:
$$F=F_{A}=I B operatorname{lsin} alpha$$
где $alpha$ – искомый угол. Следовательно:
$$alpha=arcsin left(frac{F}{I B l}right)$$
Ответ. $alpha=arcsin left(frac{F}{I B l}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
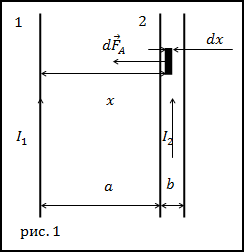
Задание. Два тонких, длинных проводника с токами лежат в одной плоскости на расстоянии d друг от друга.
Ширина правого проводника равна a. По проводникам текут токи I1 и I2 (рис.1). Какова, сила Ампера, действующая
на проводники в расчете на единицу длины?
Решение. За основу решения задачи примем формулу элементарной силы Ампера:
$$d bar{F}_{A}=I d bar{l} times bar{B}(2.1)$$
Будем считать, что проводник с током I1 создает магнитное поле, а другой проводник в нем находится.Станем искать силу
Ампера, действующую на проводник с током I2. Выделим в проводнике (2) маленький элемент dx (рис.1), который находится
на расстоянии x от первого проводника. Магнитное поле, которое создает проводник 1 (магнитное поле бесконечного прямолинейного проводника с
током) в точке нахождения элементаdxпо теореме о циркуляции можно найти как:
$$B cdot 2 pi x=mu_{0} I_{1} rightarrow B=frac{mu_{0} I_{1}}{2 pi x}$$
Вектор магнитной индукции в точке нахождения элемента dx направлен перпендикулярно плоскости
рисунка, следовательно, модуль элементарной силы Ампера, действующий на него можно представить как:
$$B cdot 2 pi x=mu_{0} I_{1} rightarrow B=frac{mu_{0} I_{1}}{2 pi x}$$
где ток, который течет в элементе проводника dx, выразим как:
$$B cdot 2 pi x=mu_{0} I_{1} rightarrow B=frac{mu_{0} I_{1}}{2 pi x}$$
Тогда выражение для dFA, учитывая (2.2) и (2.4) запишем как:
$$B cdot 2 pi x=mu_{0} I_{1} rightarrow B=frac{mu_{0} I_{1}}{2 pi x}$$
где из рис.1 видно, что $a leq x leq a+b$, по условию задачи силу следует
найти на единицу длины, значит $0 leq l leq 1$ . Для нахождения суммарной силы Ампера, действующей на проводник (2) возьмем двойной интеграл от выражения (2.5):
$$F_{A}=int_{a}^{a+b} int_{0}^{1} frac{mu_{0} I_{1}}{2 pi x} cdot frac{I_{2}}{b} d x d l=int_{a}^{a+b} frac{mu_{0} I_{1}}{2 pi x} cdot frac{I_{2}}{b} d x=frac{mu_{0} I_{1}}{2 pi} cdot frac{I_{2}}{b} ln left|frac{a+b}{a}right|$$
Проводники действуют друг на друга с силами равными по модулю и так как токи направлены одинаково, то они притягиваются.
Ответ. $F_{A}=frac{mu_{0} I_{1}}{2 pi} cdot frac{I_{2}}{b} ln left|frac{a+b}{a}right|$
Читать дальше: Формула силы выталкивания.
Содержание:
Сила и закон Ампера:
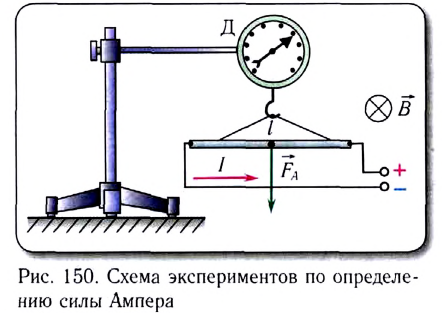
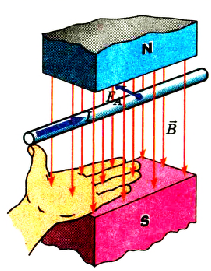
Действие магнитного поля на проводник с током в 1820 г. исследовал экспериментально Андре Мари Ампер. Меняя форму проводников и их расположение в магнитном поле, Ампер сумел определить силу, действующую на отдельный участок проводника с током (элемент тока). В его честь ее назвали силой Ампера.
Исследуем с помощью динамометра модуль силы Ампера, действующей на участок прямолинейного проводника длиной I с током силой l со стороны магнитного поля индукцией В (рис. 150).
Согласно экспериментальным данным и результатам вычислений модуль силы:
- пропорционален длине проводника, находящегося в магнитном поле (F ~ l)
- пропорционален модулю индукции магнитного поля (F ~ В); пропорционален силе тока в проводнике (F ~ l);
- зависит от ориентации проводника в магнитном поле, т. е. от угла
Обобщая полученные результаты, запишем выражение для силы Ампера
в виде
где В — индукция магнитного поля, l — длина участка проводника, находящегося в магнитном поле, I — сила тока в проводнике, 
Закон Ампера
Это выражение называют законом Ампера:
- модуль силы, с которой магнитное поле действует на находящийся в нем прямолинейный проводник с током, равен произведению индукции В этого поля, силы тока I, длины участка проводника l и синуса угла между направлениями тока и индукции магнитного поля.
Сила Ампера 
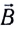
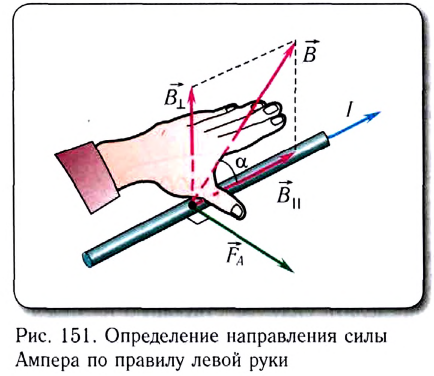
Правило левой руки
Ампера используют правило левой руки (рис. 151):
если ладонь левой руки расположить так, чтобы перпендикулярная к проводнику составляющая вектора индукции магнитного поля входила в ладонь, а четыре вытянутых пальца указывали направление тока, то отогнутый на 90° большой палец укажет направление силы Ампера.
Магнитное взаимодействие проводников с током используется для определения в СИ одной из основных единиц — единицы силы тока — ампера.
Один ампер есть сила постоянного тока, поддерживаемого в каждом из двух прямолинейных параллельных проводниках бесконечной длины и ничтожно малого кругового сечения, расположенных на расстоянии 1 м один от другого в вакууме, который вызывает между этими проводниками силу взаимодействия, равную 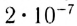
Магнитное поле
Обобщение учеными результатов теоретических и экспериментальных исследований различных взаимодействий в природе привело к выводу, что материя может существовать не только в форме вещества, по и в форме поля. Изучая физику в предыдущих классах, вы узнали о существовании электрического и магнитного полей, благодаря которым взаимодействуют наэлектризованные тела. Работы Дж. Максвелла, М. Фарадея и других ученых показали, что эти поля взаимосвязаны и фактически являются проявлениями более универсального электромагнитного поля. И только выбор системы отсчета определяет, что мы наблюдаем — электрическое или магнитное поле. Изучить все свойства электромагнитного поля довольно сложно. Поэтому в физике изучают постепенно отдельные проявления этого ноля. Одним из этапов изучения электромагнитного поля является изучение магнитного поля, которое проявляется в случае, когда заряженные частицы или тела в определенной системе отсчета движутся равномерно. В этом разделе рассматриваются не только условия, при которых магнитное поле наблюдается, но и физические величины, которые описывают его свойства, законы, по которым взаимодействуют магнитные поля и вещественные объекты. Знание этих законов позволяет производить важные для практики расчеты результатов взаимодействия магнитного поля с различными физическими телами.
Явления, которые мы называем магнитными, известны человечеству очень давно. Необычные свойства магнетита (разновидности железной руды) использовались в Древнем Китае, а потом и в других странах для изготовления компасов. Магнитам приписывали магические свойства, их действием объясняли непонятные явления природы, пробовали лечить болезни.
Систематизированные исследования магнитов провел английский физик У. Гильберт в XVI в. Он не только исследовал взаимодействие постоянных .магнитов, но и установил, что Земля является большим магнитом.
Учение о магнитах развивалось длительное время обособленно, как отдельная отрасль науки, пока ряд открытий и теоретических исследований в XIX в. не доказали его органическую связь с электричеством.
Одним из фундаментальных доказательств единства электрических и магнитных явлений является опыт Г.Х. Эрстеда, датского физика, который в 1820 г. заметил, что магнитная стрелка изменяет ориентацию вблизи проводника с током (рис. 2.1).
Pиc. 2.1. Опыт Эрстеде
Было вполне очевидно, что причиной изменения ориентации стрелки является электрический ток -направленное движение заряженных частиц в проводнике. C подробным описанием этого опыта вы встречались в 9-м классе.
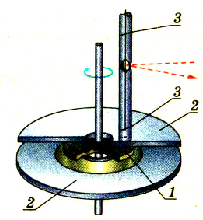
Магнитное действие движущихся заряженных тел исследовал также американский физик Г. Роуланд в 1878 г. Основная часть его установки представляла собой эбонитовый диск 1, покрытый тонким слоем золота (рис. 2.2). Диск был насажен на вал и мог свободно вместе с ним вращаться между двумя стеклянными пластинами 2. Над эбонитовым диском были укреплены на тонкой нити две намагниченные стальные иголки 3, чувствительные к магнитному полю. Когда диску сообщили некоторый заряд и начали вращать, иголки повернулись на некоторый угол, что свидетельствовало о наличии магнитного поля. При увеличении скорости вращения иголки поворачивались на больший угол.
Рис. 22. Главная часть установки Роуланда по выявлению магнитного поля движущегося электрически заряженного диска
Опытами Г. Роуланда было подтверждено открытие Эрстеда о связи магнитного поля с движущимися электрически заряженными частицами или телами.
 |
Генри Роуланд (184β-1901) — американский физик; научные работы в области электродинамики, оптики, спектроскопии и теплоты. Он доказал, что заряженные тела, если они движутся, вызывают магнитное взаимодействие. |
Магнитные явления хотя и связаны с электрическими, но не идентичны им. Это подтверждают опыты.
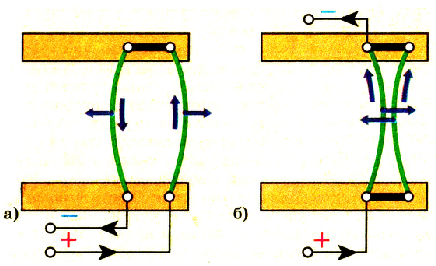
Если взять два длинных параллельных проводника и присоединить к источнику тока, то заметим, что они взаимодействуют между собой (рис. 2.3) в зависимости от направления тока в них. При токах противоположных направлений проводники отталкиваются (рис. 2.3-а). Если токи одного направления, то проводники притягиваются друг к другу (рис. 2.3-б).
Pиc. 23. Магнитное взаимодействие проводников с током
Действие проводника с током на магнитную стрелку или другой проводник с током происходит при отсутствии непосредственного контакта между ними, благодаря наличию вокруг проводника магнитного поля.
Магнитное поле имеет свои особенности, которые выделяют его среди других полей:
- магнитное поле наблюдается всегда, когда есть движущиеся заряженные частицы или тела;
- магнитное поле действует только на движущиеся заряженные тела или частицы.
Другие свойства будут описаны далее.
Магнитная индукция
Наблюдения за магнитными взаимодействиями в лаборатории или в природе показывают, что действия магнитного поля па физические тела или проводники с током при равных условиях могут быть различными.
Интенсивность магнитного взаимодействия может быть различной.
Если для выявления магнитного поля Земли магнитную стрелку компаса приходится устанавливать на специальных опорах, которые существенно уменьшают силы трения, то действие электромагнита, в обмотках которого проходит электрический ток, будет заметным даже тогда, когда стрелка будет просто лежать на столе.
Различным будет и взаимодействие параллельных проводников с током. Сила взаимодействия этих проводников будет изменяться, если будет изменяться сила тока в них или расстояние между ними, — она будет увеличиваться при увеличении силы тока или при уменьшении расстояния.
Для всех таких случаев говорят о «сильном» или «слабом» поле. Аналогичные случаи рассматривались при изучении свойств электрического поля, при рассмотрении действия электрического поля на заряженные тела. Для количественной характеристики электрического поля введена напряженность электрического поля. Для магнитного же поля используется также силовая характеристика и соответствующая ей физическая величина магнитная индукция. Магнитная индукция является векторной величиной и обозначается буквой В. Поскольку для исследования магнитного поля длительное время пользовались магнитной стрелкой на острие, то магнитная индукция как характеристика магнитного поля была связана с действием магнитного поля па магнитную стрелку. Так, направление полюсов стрелки послужило базой для установления направления вектора магнитной индукции изучаемого поля. Условились, что за направление магнитной индукции принимается направление северного полюса стрелки.
Магнитная индукция — векторная величина, имеющая направление.
Исследуем с помощью магнитной стрелки магнитное поле проволочного витка с током.
Замкнув цепь, в которую включен виток, начнем обносить магнитную стрелку на острие вокруг витка. Заметим, что ориентация стрелки при этом будет меняться. В разных точках она будет иметь различную ориентацию. Наиболее ощутимым будет действие поля на стрелку в центре витка (рис. 2.4).
Puc. 2.4. Продольная ось магнитной стрелки, находящаяся в центре витка с током, перпендикулярна его плоскости
Таким образом, мы установили, что магнитная индукция витка или прямоугольной рамки будет иметь максимальное значение в центре.
Продольная ось магнитной стрелки плоскости витка. Аналогичное явление будет наблюдаться и тогда, когда возьмем прямоугольную рамку или моток провода произвольной формы.
В отличие от напряженности электрического поля магнитная индукция как векторная величина не совпадает по направлению с направлением силы, которая действует на проводник с током. Выясним, как направление вектора магнитной индукции зависит от направления тока в витке.
Магнитная индукция — это силовая характеристика поля. Она определяет силу, которая действует на проводник с током или на движущуюся частицу.
Отметив направление магнитной стрелки при определенном направлении тока в витке, изменим направление последнего на противоположное. Магнитная стрелка развернется на 1800, показывая, что направление магнитной индукции также изменилось. Таким образом, направление магнитной индукции витка с током зависит от направления тока и нем.
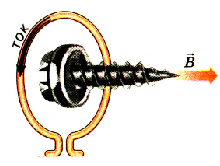
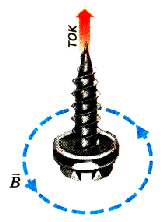
Чтобы каждый раз, когда нужно знать направление магнитной индукции, не проводить опыты со стрелкой, пользуются правилом правого винта (буравчика).
Это правило позволяет запомнить связь направления тока в витке с направлением магнитной индукции его поля. Для этого необходимо представить, как будет двигаться правый винт, приставленный перпендикулярно к плоскости витка, при вращении его по направлению тока в витке.
Если направление вращения правого винта, расположенного в центре витка с током, совпадает с направлением тока, то его поступательное движение показывает направление магнитной индукции (рис. 2.5).
Магнитное поле существует и вокруг прямого проводника с током. Для подтверждения этого магнитную стрелку будем обносить вокруг проводника, не изменяя расстояния (рис. 2.6).
|
Pиc. 2.5. Определение |
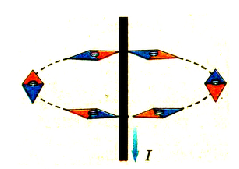 Pиc. 2.6. Исследование магнитного поля прямого проводника с током при помощи магнитной стрелки |
В разных точках ее ориентация будет различной, но ось стрелки всегда будет направлена по касательной к траектории движения.
Соответственно и магнитная индукция проводника с током будет иметь такое ясе направление.
При изменении направления тока в проводнике на противоположное стрелка развернется на 180° и покажет направление магнитной индукции, которое также будет противоположным к прежнему.
Таким образом, направление магнитной индукции прямого проводника зависит от направления тока в нем. Для облегчения его определения, как и в предыдущем случае, на основании анализа результатов эксперимента, сформулировано правило правого винта (рис. 2.7): если направление поступательного движения правого винта совпадает с направлением тока в проводнике, то направление его вращения показывает направление магнитной индукции.
Pиc. 2.7. Определение направления магнитной индукции поля прямого проводника с током при помощи правою винта (буравчика)
Для измерения магнитной индукции применяется специальная единица тесла (Тл). Эта единица названа в честь сербского ученого и изобретателя Николы Теслы.
 |
Никола Тесла (1856-1943) — родился в Сербии, изобретатель и физик. Известен благодаря своим изобретениям в области электротехники и электроники; работал инженером на предприятиях Венгрии, Франции, США. |
В практике используются долевые величины:
- 1 миллитесла = 1 мТл = 10-3 Тл,
- 1 микротесла 1 мкТл 10-6 Тл.
Значения магнитной индукции измеряют специальными приборами, которые называются магнитометрами или индикаторами магнитной индукции (рис. 2.8).
Pиc. 2.8. Лабораторный магнитометр для школьных опытов
Часто вместо прямых измерений пользуются формулами, которые позволяют рассчитать магнитную индукцию на основании параметров проводника. Таким примером может быть расчет модуля магнитной индукции прямого проводника с током. Экспериментально подтверждено, что магнитная индукция поля прямого проводника с током прямо пропорциональна силе тока в проводнике и обратно пропорциональна расстоянию от его оси:
Магнитная индукция прямого проводника с током пропорциональна силе тока в нем и обратно пропорциональна расстоянию от проводника до точки наблюдения.
Коэффициент пропорциональности в этой формуле зависит от выбора системы единиц измерений. В Международной системе единиц (СИ) он имеет значение
где μ0 — магнитная постоянная, ее числовое значение 1,256 × × 10-6 Н/А2.
Тогда окончательно для рассчетов модуля магнитной индукции поля прямого проводника с током имеем формулу:
где μ0 — магнитная постоянная; I — сила тока в проводнике: r — расстояние от проводника до данной точки поля.
Пример №1
Каково значение модуля магнитной индукции в точке поля, удаленной на 3 см от бесконечно длинного проводника, по которому проходит ток 6 А?
| Дано: r = 3 см, I = 6 А. |
Решение Магнитная индукция прямого проводника с током рассчитывается по формуле: 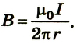 |
| В — ? |
Подставив значения физических величин, получим
Ответ: магнитная индукция поля прямого проводника с током равна 4 • 10-5 Тл.
Действие магнитного поля на проводник с током и сила Ампера
Поскольку вокруг проводников с током возникает магнитное поле, естественно предположить, что в магнитном поле на них действует сила.
На проводник с током в магнитном поле действует сила.
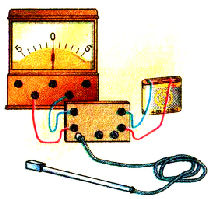
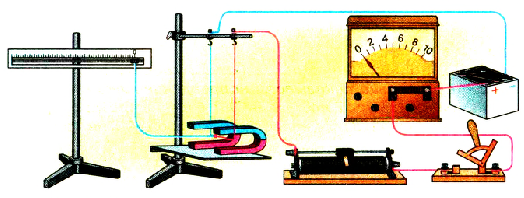
Проведем исследование с целью определения, от чего зависит модуль и направление этой силы. Для этого используем установку, в которой прямой проводник подвешен в магнитном поле постоянного магнита так, что его можно включать в электрическую цепь, силу тока в которой можно изменять при помощи реостата. Амперметр будет измерять силу тока в цепи.
Замкнув электрическую цепь, заметим, что проводник отклонится от положения равновесия, а динамометр покажет некоторое значение силы. Увеличим силу тока в проводнике в 2 раза и увидим, что сила, действующая на проводник, также увеличится в 2 раза. Любые другие изменения силы тока будут вызывать соответствующие изменения силы. Сопоставление результатов всех измерений позволяет сделать вывод, что сила F, которая действует на проводник с током, пропорциональна силе тока к нем:
F~I.
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
Сила Ампера пропорциональна силе тока в проводнике.
Pиc. 2.9. Установка для изучения действия магнитного поля на проводник с током
Расположим еще один магнит рядом с первым. Длина проводника, находящегося в магнитном поле, увеличится приблизительно в 2 раза. Значение силы, действующей на проводник, в этом случае также увеличится в 2 раза. Таким образом, сила FΔ, действующая на проводник с током в магнитном поле, пропорциональна длине проводника Δl, который расположен в магнитном поле:
F~ΔI.
Сила Ампера пропорциональна длине активной части проводника.
Сила увеличится также тогда, когда применим другой, более мощный магнит с большей магнитной индукцией поля.
Это позволит сделать вывод, что сила Ампера FА зависит от магнитной индукции поля:
F~B.
Опыт позволяет убедиться и в том, что наибольшее значение силы Ампера будет тогда, когда угол между проводником и вектором магнитной индукции будет равен 90°. Если этот угол будет равен нулю, т. е. вектор магнитной индукции будет параллельным проводнику, то сила Ампера также будет равна нулю. Отсюда легко сделать вывод, что сила Ампера зависит от угла между вектором магнитной индукции и проводником.
Окончательно для расчетов имеем формулу
Направление силы Ампера определяется по правилу левой руки (рис. 2.10): если левую руку разместить так, чтобы линии магнитной индукции входили в ладонь, а четыре от. ставленных пальца показывали направление тока в проводнике, то отставленный под углом 90″ большой палец покажет направление силы, действующей на проводник с током в магнитном поле.
Pиc. 2.10. При помощи левой pуκu можно определить направление силы Ампера
Если левую руку разместить так. чтобы линии магнитной индукции входили в ладонь, а четыре отставленных пальца показывали направление тока в проводнике, то отставленный под углом 90° большой палец покажет направление силы, действующей на проводник с током в магнитном поле.
Взаимодействие проводников с током
Взаимодействие проводников с током объясняется действием силы Ампера (рис. 2.11).
Каждый из проводников имеет свое магнитное поле, которое действует на соседний проводник с током и способствует появлению силы Ампера. Так, проводник AA‘ по которому проходит ток I1, имеет магнитное поле, модуль индукции B1 которого, как указывалось ранее, равен
где r — расстояние от проводника до точки наблюдения.
Если проводник CC’ длиной Δl находитсяy на расстоянии r от проводника AA’ и в нем проходит ток I2, то на него действует сила Ампера FА, поскольку он находится в магнитном поле проводника AA’ . Значение этой силы равно
Поскольку проводники параллельны и угол между проводником CC’ и вектором магнитной индукции B1 равен 90°, то sinα = 1.
Подставим в последнюю формулу значение магнитной индукции поля проводника AA’:
Силу взаимодействия двух параллельных проводников с током можно определить, зная только расстояние между ними и силу тока в них.
Как и при любом взаимодействии, такая сила, согласно третьему закону Ньютона, действует на каждый из проводников. Только направления их противоположны.
Таким образом, два параллельных проводника нзнимодей-ствуют между собой благодаря магнитным полям, которые образуются вокруг проводников, по которым проходит электрический ток.
Пример №2
Определить модуль силы Ампера, которая действует на проводник с током длиной 25 см в магнитном поле с индукцией 0,04 Тл, если между вектором магнитной индукции и направлением тока угол 30° сила тока в проводнике 0,25 А.
|
Дано: |
Решение Подставим значения всех величин: |
| FA— ? |
Ответ: модуль силы равен 1,25 • 10-3 Н.
Использование действия силы Ампера
Силу Ампера применяют для преобразования энергии электрического тока в механическую энергию проводника. Такое превращение происходит во многих электротехнических устройствах. Рассмотрим некоторые из них.
Eлектроиэмеритальные приборы магнитоэлектрической системы
Электроизмерительный прибор магнитоэлектрической системы состоит из постоянного магнита и проволочной рамки, расположенной между его полюсами (рис. 2.12). Полюса магнита имеют специальные насадки, создающие однородное магнитное поле, в котором вращение рамки не приводит к изменению угла между магнитной индукцией и проводниками рамки. Этот угол всегда равен 90°.
Pиc. 2.12. Устройство электроизмерительного прибора магнитоэлектрической системы
C рамкой соединены две спиральные пружины, которые подводят к рамке электрический ток. Во время прохождения электрического тока по витком рамки возникает сила Ампера, пропорциональная силе тока в рамке. Чем больше сила действует на витки рамки, тем больше закручиваются спиральные пружины, которых возникает сила упругости. Когда сила Ампера и сила упругости станут равными, вращение рамки прекратится.
Стрелка, прикрепленная к рамке, показывает угол поворота рамки. Этот угол пропорционален силе тока в рамке.
Электрический двигатель постоянного тока
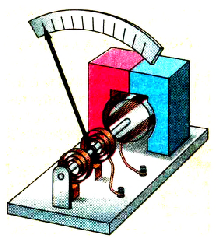
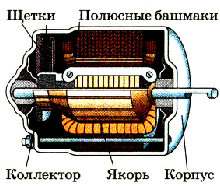
Электрический двигатель применяют для преобразования энергии электрического тока в механическую энергию вращения вала двигателя. Принцип его действия подобен принципу действия электроизмерительного прибора магнитоэлектрической системы, описанного выше. Только в его конструкции отсутствует пружина, поэтому рамка может поворачиваться на любой угол. Электрический ток к рамке, размещенной на валу и имеющей стальной сердечник, подается через специальные скользящие контакты-щетки (рис. 2.13).
Рис. 213. Устройство двигателя постоянного тока
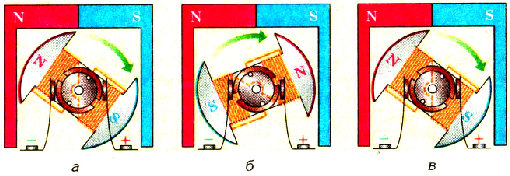
При замыкании цепи питания двигателя ток проходит по рамке и она взаимодействует с магнитным полем постоянного магнита или электромагнита и поворачивается до тех пор, пока ее плоскость не станет параллельной вектору магнит ной индукции. Чтобы она могла нужно сменить направление силы тока в ней, вследствие чего поменяет направлению сила Ампера, действующая на рамку с током в магнитном поле. В двигателе этот процесс осуществляется с помощью двух неподвижных графитометаллических щеток и двух полуколец на валу, к которым подведены концы рамки.
На рисунке 2.14-а показан момент, когда ток в якоре такого направления, что его полюса отталкиваются от одноименных полюсов статора. После поворачивания на некоторый угол якорь окажется в положении, когда разноименные полюса притягиваются (рис 2.14-6). Вследствие инерции якорь проходит это положение равновесия, а благодаря кольцам, которых касаются токоподводящие щетки (рис. 2.14-в), направление тока в якоре изменяется па противоположное и вращение якоря продолжается (см. рис. 2.14-а).
Pиc. 2.14 Схемы, которые объясняют действие коллекторного электродвигателя постоянного тока
В промышленных образцах электродвигателей постоянного тока ротор имеет несколько рамок-обмоток. Поэтому и количество пар скользящих контактов в них больше: оно согласуется с количеством обмоток. В целом такое устройство называют коллектором. В новейших моделях двигателей постоянного тока роль коллектора выполняет специальное устройство с электронными приборами.
Таким образом, действие силы Ампера нашло применение в различных технических устройствах: электроизмерительных приборах, электрических двигателях и т. п.
Сила ампера
Вы узнали, что магнитное поле действует на проводник с током с некоторой силой. А из курса физики 8 класса помните, что сила — это векторная физическая величина, поэтому, чтобы полностью определить силу, нужно уметь рассчитывать ее значение и определять направление. От чего зависит значение силы, с которой магнитное поле действует на проводник с током, как направлена эта сила и почему ее называют силой Ампера, вы узнаете из данного параграфа.
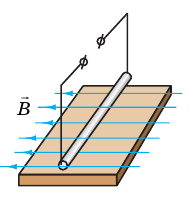
Характеристика силы действующей на проводник с током
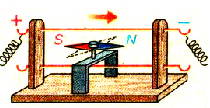
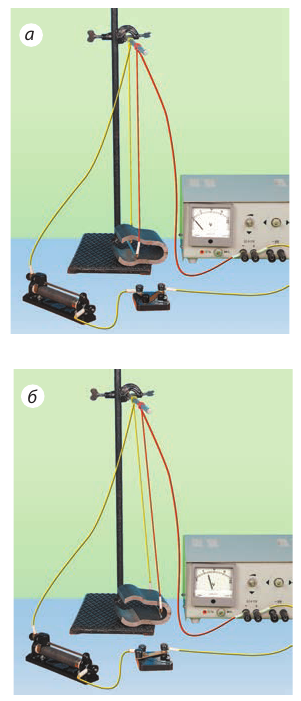
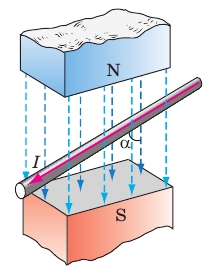
Между полюсами подковообразного постоянного магнита подвесим на тонких и гибких проводах прямой алюминиевый проводник (рис. 4.1, а). Если через проводник пропустить ток, проводник отклонится от положения равновесия (рис. 4.1, б). Причина такого отклонения — сила, действующая на проводник с током со стороны магнитного поля. Доказал наличие этой силы и выяснил, от чего зависят ее значение и направление, А. Ампер. Именно потому эту силу называют силой Ампера.
Рис. 4.1. Опыт, демонстрирующий действие магнитного поля на алюминиевый проводник: при отсутствии тока магнитное поле на проводник не действует (а); если в проводнике течет ток, на проводник действует магнитное поле и проводник отклоняется (б)
Сила Ампера — это сила, с которой магнитное поле действует на проводник с током.
Сила Ампера прямо пропорциональна силе тока в проводнике и длине активной части проводника (то есть части, расположенной в магнитном поле). Сила Ампера увеличивается с увеличением индукции магнитного поля и зависит от того, под каким углом к линиям магнитной индукции расположен проводник.
Значение силы Ампера 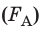
где 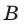
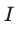
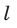
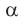
Обратите внимание! Магнитное поле не будет действовать на проводник с током 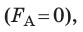
Рис. 4.2. Угол 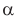
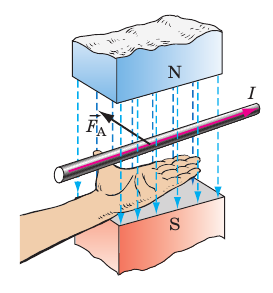
Чтобы определить направление силы Ампера, используют правило левой руки:
Если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца указывали направление тока в проводнике, то отогнутый на 90° большой палец укажет направление силы Ампера (рис. 4.3).
Рис. 4.3. Определение направления силы Ампера по правилу левой руки
Формула для определения модуля магнитной индукции
Если проводник расположен перпендикулярно линиям магнитной индукции 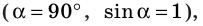
Отсюда получаем формулу для определения модуля магнитной индукции:
Обратите внимание! Значение магнитной индукции не зависит ни от силы тока в проводнике, ни от длины проводника, а зависит только от свойств магнитного поля.
Например, если уменьшить силу тока в проводнике, то уменьшится и сила Ампера, с которой магнитное поле действует на проводник, а вот значение магнитной индукции останется неизменным.
В СИ единица магнитной индукции — тесла (Тл), единица силы — ньютон (Н), силы тока — ампер (А), длины — метр (м), поэтому:
1 Тл — это индукция такого однородного магнитного поля, которое действует с максимальной силой 1 Н на проводник длиной 1 м, в котором течет ток силой 1 А.
- Заказать решение задач по физике
Пример №3
Докажите, что два параллельных проводника, в которых текут токи одного направления, притягиваются.
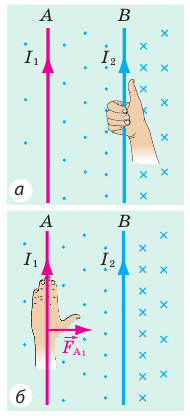
Анализ физической проблемы. Около любого проводника с током существует магнитное поле, следовательно, каждый из двух проводников находится в магнитном поле другого. На первый проводник действует сила Ампера со стороны магнитного поля, созданного током во втором проводнике, и наоборот. Определив по правилу левой руки направления этих сил, выясним, как будут вести себя проводники.
Решение
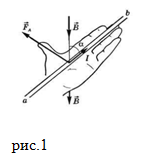
Решая задачу, выполним пояснительные рисунки: изобразим проводники А и В, покажем направления тока в них и т. д.
Выясним направление силы Ампера, которая действует на проводник А, находящийся в магнитном поле проводника В.
- С помощью правила буравчика найдем направление линий магнитной индукции магнитного поля, созданного проводником В (рис. 1, а). Выясняется, что вблизи проводника А магнитные линии направлены к нам (обозначено «•»).
- Воспользовавшись правилом левой руки, определим направление силы Ампера, действующей на проводник А со стороны магнитного поля проводника В (рис. 1, б).
Рис. 1
3. Приходим к выводу: проводник А притягивается к проводнику В.
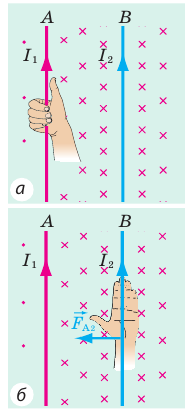
Теперь выясним направление силы Ампера, которая действует на проводник В, находящийся в магнитном поле проводника А.
1) Определим направление линий магнитной индукции магнитного поля, созданного проводником А (рис. 2, а). Выясняется, что вблизи проводника В магнитные линии направлены от нас (обозначено
2) Определим направление силы Ампера, действующей на проводник В (рис. 2, б).
Рис. 2
3) Приходим к выводу: проводник В притягивается к проводнику А.
Ответ: два параллельных проводника, в которых текут токи одного направления, притягиваются.
Пример №4
Прямой проводник (стержень) длиной 0,1 м и массой 40 г находится в горизонтальном однородном магнитном поле индукцией 0,5 Тл. Стержень расположен перпендикулярно магнитным линиям поля (рис. 3).
Рис. 3
Ток какой силы и в каком направлении следует пропустить по стержню, чтобы стержень не давил на опору (завис в магнитном поле)?
Анализ физической проблемы. Стержень не будет давить на опору, если сила Ампера уравновесит силу тяжести. Это произойдет при условиях: 1) сила Ампера будет направлена противоположно силе тяжести (то есть вертикально вверх); 2) значение силы Ампера будет равно значению силы тяжести:
Дано:
Найти:
Поиск математической модели, решение
1. Определим направление тока. Для этого расположим левую руку так, чтобы линии магнитного поля входили в ладонь, а отогнутый на 90° большой палец был направлен вертикально вверх. Четыре вытянутых пальца укажут направление от нас. Следовательно, ток в проводнике нужно направить от нас.
2. Учитываем, что
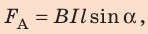
Следовательно,
Из последнего выражения найдем силу тока:
Проверим единицу, найдем значение искомой величины.
Вспомним:
Ответ: 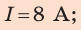
Подводим итоги:
Силу, с которой магнитное поле действует на проводник с током, называют силой Ампера. Значение силы Ампера находят по формуле: 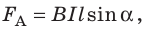
Направление силы Ампера определяют по правилу левой руки: если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца указывали направление тока в проводнике, то отогнутый на 90° большой палец укажет направление силы Ампера.
Магнитные свойства веществ и гипотеза Ампера
Наверное, каждый из вас видел магниты и даже исследовал их свойства. Если поднести магнит к кучке мелких предметов, некоторые из них (гвоздики, кнопки, скрепки) притянутся к магниту, а некоторые (кусочки мела, медные и алюминиевые монетки, комочки земли) никак не отреагируют. Почему так? Действительно ли магнитное поле не оказывает никакого влияния на некоторые вещества? Именно об этом пойдет речь в параграфе.
Действия электрического и магнитного полей на вещество
Изучая в 8 классе электрические явления, вы узнали, что под влиянием внешнего электрического поля происходит перераспределение электрических зарядов внутри незаряженного тела (рис. 5.1). В результате в теле образуется собственное электрическое поле, направленное противоположно внешнему, и именно поэтому электрическое поле в веществе всегда ослабляется.
Рис. 5.1. В результате действия электрического поля отрицательно заряженной палочки ближняя к ней часть проводящей сферы приобретает положительный заряд
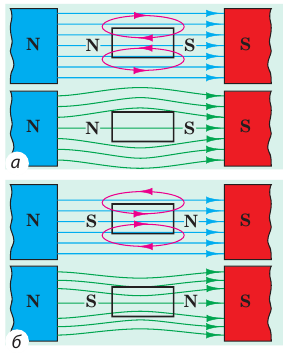
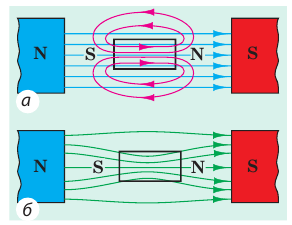
Вещество изменяет и магнитное поле. Есть вещества, которые (как в случае с электрическим полем) ослабляют магнитное поле внутри себя. Такие вещества называют диамагнетиками. Многие вещества, наоборот, усиливают магнитное поле — это парамагнетики и ферромагнетики.
Дело в том, что любое вещество, помещенное в магнитное поле, намагничивается, то есть создает собственное магнитное поле, магнитная индукция которого разная для разных веществ.
Слабомагнитные вещества
Вещества, которые намагничиваются, создавая слабое магнитное поле, магнитная индукция которого намного меньше магнитной индукции внешнего магнитного поля (то есть поля, вызвавшего намагничивание), называют слабомагнитными веществами. К таким веществам относятся диамагнетики и парамагнетики.
Диамагнетики (от греч. dia — расхождение) намагничиваются, создавая слабое магнитное поле, направленное противоположно внешнему магнитному полю (рис. 5.2, а). Именно поэтому диамагнетики незначительно ослабляют внешнее магнитное поле: магнитная индукция магнитного поля внутри диамагнетика 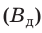
Рис. 5.2. Образцы из диамагнетика (а) и парамагнетика (б) во внешнем магнитном поле: красные линии — линии магнитного поля, созданного образцом; синие — магнитные линии внешнего магнитного поля; зеленые — линии результирующего магнитного поля
Если диамагнетик поместить в магнитное поле, он будет выталкиваться из него (рис. 5.3).
Рис. 5.3. Пламя свечи выталкивается из магнитного поля, так как продукты сгорания — диамагнитные частицы
К диамагнетикам относятся инертные газы (гелий, неон и др.), многие металлы (золото, медь, ртуть, серебро и др.), молекулярный азот, вода и т. д. Тело человека — диамагнетик, так как оно в среднем на 78 % состоит из воды.
Парамагнетики (от греч. para — рядом) намагничиваются, создавая слабое магнитное поле, направленное в ту же сторону, что и внешнее магнитное поле (рис. 5.2, б). Парамагнетики незначительно усиливают внешнее поле: магнитная индукция магнитного поля внутри парамагнетика 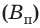
К парамагнетикам относятся кислород, платина, алюминий, щелочные и щелочноземельные металлы и другие вещества. Если парамагнитное вещество поместить в магнитное поле, то оно будет втягиваться в это поле.
Ферромагнетики
Если слабомагнитные вещества извлечь из магнитного поля, их намагниченность сразу исчезнет. Иначе происходит с сильномагнитными веществами — ферромагнетиками.
Ферромагнетики (от лат. ferrum — железо) — вещества или материалы, которые остаются намагниченными и при отсутствии внешнего магнитного поля.
Ферромагнетики намагничиваются, создавая сильное магнитное поле, направленное в ту же сторону, что и внешнее магнитное поле (рис. 5.4, 5.5, а). Если изготовленное из ферромагнетика тело поместить в магнитное поле, оно будет втягиваться в него (рис. 5.5, б).
Рис. 5.4. Железный гвоздь намагничивается в магнитном поле так, что конец гвоздя, расположенный вблизи северного полюса магнита, становится южным полюсом, поэтому гвоздь притягивается к магниту
Рис. 5.5. Ферромагнетики создают сильное магнитное поле, направленное в ту же сторону, что и внешнее магнитное поле (а); линии магнитной индукции как будто втягиваются в ферромагнитный образец (б)
К ферромагнетикам относится небольшая группа веществ: железо, никель, кобальт, редкоземельные вещества и ряд сплавов. Ферромагнетики значительно усиливают внешнее магнитное поле: магнитная индукция магнитного поля внутри ферромагнетиков 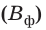
Так, кобальт усиливает магнитное поле в 175 раз, никель — в 1120 раз, а трансформаторная сталь (на 96-98 % состоит из железа) — в 8000 раз.
Ферромагнитные материалы условно делят на два типа. Материалы, которые после прекращения действия внешнего магнитного поля остаются намагниченными длительное время, называют магнитожесткими ферромагнетиками. Их применяют для изготовления постоянных магнитов. Ферромагнитные материалы, которые легко намагничиваются и быстро размагничиваются, называют магнитомягкими ферромагнетиками. Их применяют для изготовления сердечников электромагнитов, двигателей, трансформаторов, то есть устройств, которые во время работы постоянно перемагничиваются (о строении и принципе действия таких устройств вы узнаете позже).
Обратите внимание! При достижении температуры Кюри (см. таблицу) ферромагнитные свойства магнитомягких и магнитожестких материалов исчезают — материалы становятся парамагнетиками.
Температура Кюри для некоторых ферромагнетиков
| Вещество (или материал) | Температура,°С |
| Гадолиний | +19 |
| Железо | +770 |
| Кобальт | +1127 |
| Неодимовый магнит NdFeB | +320 |
| Никель | +354 |
Гипотеза Ампера
Наблюдая действие проводника с током на магнитную стрелку (см. рис. 1.1) и выяснив, что катушки с током ведут себя как постоянные магниты (см. рис. 1.3), А. Ампер выдвинул гипотезу о магнитных свойствах веществ. Ампер предположил, что внутри веществ существует огромное количество незатухающих малых круговых токов и каждый из них, как маленькая катушка, является магнитиком. Постоянный магнит состоит из множества таких элементарных магнитиков, ориентированных в определенном направлении.
Механизм намагничивания веществ Ампер объяснял так. Если тело не намагничено, круговые токи ориентированы беспорядочно (рис. 5.7, а). Внешнее магнитное поле пытается сориентировать эти токи так, чтобы направление магнитного поля каждого тока совпадало с направлением внешнего
Рис. 5.7. Механизм намагничивания тел согласно гипотезе Ампера: а — круговые токи ориентированы беспорядочно, тело не намагничено; б — круговые токи ориентированы в определенном направлении, тело намагничено
магнитного поля (рис. 5.7, б). У некоторых веществ такая ориентация токов (намагничивание) остается и после прекращения действия внешнего магнитного поля. Таким образом, все магнитные явления Ампер объяснял взаимодействием движущихся заряженных частиц.
Гипотеза Ампера послужила толчком к созданию теории магнетизма. На основе этой гипотезы были объяснены известные свойства ферромагнетиков, однако она не могла объяснить природу диа- и парамагнетизма, а также то, почему только небольшое количество веществ имеет ферромагнитные свойства. Современная теория магнетизма основана на законах квантовой механики и теории относительности А. Эйнштейна.
Подводим итоги:
Любое вещество, помещенное в магнитное поле, намагничивается, то есть создает собственное магнитное поле.
| Диамагнетики | Парамагнетики | Ферромагнетики |
| Намагничиваются, создавая слабое магнитное поле, направленное противоположно внешнему магнитному полю | Намагничиваются, создавая слабое магнитное поле, направленное в сторону внешнего магнитного поля | Намагничиваются, создавая сильное магнитное поле, направленное в сторону внешнего магнитного поля; остаются намагниченными после прекращения действия внешнего магнитного поля |
| Незначительно ослабляют внешнее магнитное поле, выталкиваются из него | Незначительно усиливают внешнее магнитное поле, втягиваются в него | Усиливают внешнее магнитное поле в сотни и тысячи раз, втягиваются в него |
| Инертные газы, медь, золото, ртуть, серебро, азот, вода и др. Кислород, платина, алюминий, щелочные металлы и др. | Кислород, платина, алюминий, щелочные металлы и др. | Железо, никель, кобальт, редкоземельные вещества (например, неодим), ряд сплавов |
- Закон взаимодействия прямолинейных параллельных проводников с током
- Сила Лоренца
- Правило Буравчика в физике
- Шунт и добавочное сопротивление
- Работа по перемещению заряда в электростатическом поле
- Закон Ома для однородного участка электрической цепи
- Закон Ома для полной цепи
- Закон Ома для цепи переменного тока с последовательным соединением сопротивлений
На основе магнитных явлениях построено действие электротехнических устройств. Все современные электромоторы, генераторы и множество других электромеханических приборов работают по принципу взаимодействия электрического тока с окружающими его магнитными полями. Эти взаимодействия описывает знаменитый закон Ампера, названный так в честь своего первооткрывателя.
Влияние электричества на поведение магнитной стрелки впервые обнаружил Х. К. Эрстед. Он заметил, что вопреки ожиданию, магнитное поле не параллельно вектору тока, а перпендикулярно ему. Развивая выводы Эрстеда, и продолжая исследования в этом направлении, Мари Ампер установил [1], что электричество взаимодействует не только с магнитами, но и между собой. Заслуга Ампера в том, что он теоретически обосновал взаимное влияние токов и предоставил формулу, позволяющую вычислять силы этого взаимодействия.
Определение и формула
Экспериментальным путём Ампер установил, что между двумя параллельными проводниками, подключенными к постоянному току, действует притяжение (однонаправленные токи) либо отталкивание (если направления противоположные). Эти силы взаимодействия определяются параметрами токов (прямо пропорциональная зависимость), и расстоянием между проводниками (обратно пропорциональная зависимость).
Расчёт амперовой силы на единицу длины проводника осуществляется по формуле:
где F – сила, I1, I2 – величина тока в проводниках, а μ – магнитная проницаемость среды, окружающей проводники (см. рис. 1).
Природой взаимодействия является магнитное поле, образованное перемещаемыми по проводникам электрическими зарядами. Под влиянием магнитного поля на электрические заряды возникает сила магнитной индукции, которую обозначают символом B.
Линии, в каждой точке которых касательные к ним совпадают с направлением соответствующих векторов магнитной индукции, получили название линий электромагнитной индукции. Применяя мнемоническое правило буравчика, можно определить ориентацию в пространстве линий магнитной индукции. То есть, при ввинчивании буравчика в сторону, куда направлен вектор электрического тока, движение концов его рукоятки укажет направление векторов индукции.
Из сказанного выше следует, что в проводниках, с одинаково ориентированными токами, направления векторов магнитной индукции совпадают, а значит, векторы сил направлены навстречу друг к другу, что и вызывает притяжение.
Подобным образом проводники взаимодействуют не только между собой, но и с магнитными полями любой природы. Если такой проводник окажется в магнитном поле, то на элемент, расположенный в зоне действия магнита, будет действовать сила, которую именуют Амперовой:
Для вычисления модуля этой силы пользуются формулой: dF = IBlsinα , где α — угол, образованный векторами индукции и ориентацией тока.
Рассмотренную нами зависимость описывает закон Ампера, формулировка которого понятна из рисунка 2.
Не трудно сообразить, что когда α = 900, то sinα = 1. В этом случае величина F приобретает максимальное значение: F = B*L*I, где L– длина проводника, оказавшегося под действием магнитного поля.
Таким образом, из закона Ампера вытекает:
- проводник с током реагирует на магнитные поля.
- действующая сила находится в прямо пропорциональной зависимости от параметров тока, величины магнитной индукции и размеров проводника.
Обратите внимание, что на данном рисунке 3 проводник расположен под углом 90º к линиям магнитной индукции, что вызывает максимальное действие магнитных сил.
Направление силы Ампера
Принимая к сведению то, что сила – векторная величина, определим её направление. Рассмотрим случай, когда проводник с током расположен между двумя полюсами магнитов под прямым углом к линиям магнитной индукции.
Выше мы установили, что согласно закону Ампера, действующая на данный проводник сила, равна: F = B*L*I. Направление вектора рассматриваемой силы определяется по результатам векторного произведения:
Если полюса магнита статичны (неподвижны), то векторное произведение будет зависеть только от параметров электричества, в частности, от того, в какую сторону оно течёт.
Направление силы Ампера определяют по известному правилу левой руки: ладонь располагают навстречу магнитным линиям, а пальцы размещают вдоль проводника, в сторону устремления тока. На ориентацию силы Ампера указывает большой палец, образующий прямой угол с ладонью (см. рис. 4).
Измените мысленно направление электрического тока, и вы увидите, что направление вектора Амперовой силы изменится на противоположное. Модуль вектора имеет прямо пропорциональную зависимость от всех сомножителей, но на практике эту величину удобно регулировать путём изменения параметров в электрической цепи (например, для регулировки мощности электродвигателя).
Применение
Закон Ампера, а точнее следствия, вытекающие из него, используются в каждом электромеханическом устройстве, где необходимо вызвать движение рабочих элементов. Самым распространённым механизмом, работа которого базируется на законе Ампера, является электродвигатель.
Применение электромоторов настолько широкое, что его можно увидеть практически во всех сферах человеческой деятельности:
- на производстве, в качестве приводов станков и различного оборудования;
- в бытовой сфере (бытовая электротехника);
- в электроинструментах;
- на транспорте;
- в устройствах автоматики, в офисной технике и во многих других сферах.
Из закона Ампера вытекает возможность получения электротока путём перемещения проводников, находящихся в магнитном поле. На данном принципе построены все генераторы электрического тока. Благодаря этой уникальной возможности, у нас появился доступ к использованию электроэнергии для различных потребностей.
Мы буквально окружены проявлением закона Ампера. Например, просмотр телепередачи сопровождается звуком, который транслируется через динамики. Но диффузор динамика приводит в движение сила Ампера. Мы разговариваем по телефону – там тоже есть динамик и микрофон. Принцип действия современных микрофонов также основан на законе Ампера.
Вход в помещение через автоматическую раздвижную дверь, поднятие на лифте, поездка в троллейбусе, трамвае, запуск двигателя автомобиля – всё это было бы невозможным, если бы не существовало взаимодействия электрического тока с силами магнитной индукции.
Ампер открыл перед человечеством такие возможности, без которых развитие научно-технического прогресса было бы невозможным. Влияние этого закона в электротехнике сравнимо с законами Ньютона, которые в своё время совершили революцию в механике. В этом огромная заслуга учёного-физика Мари Ампера, труды которого увенчались открытием в 1820 г. знаменитого закона.
Сила Ампера
В начале (XIX) века французский физик Андре Ампер, проведя несколько серий опытов, обнаружил, что сила, которая действует в магнитном поле на проводник, по которому течёт ток, прямо пропорциональна следующим величинам:
- длине проводника;
- силе тока в этом проводнике;
- модулю вектора магнитной индукции поля.
При этом есть некоторая зависимость от угла между вектором магнитной индукции и элементом тока. Эмпирически установлено, что сила прямо пропорциональна синусу этого угла. Направление силы всегда перпендикулярно векторам магнитной индукции и элемента тока. Направление этой силы определяется по правилу левой руки.
(Delta vec{F}=k l {Delta vec{l}} times vec{B}). ((1))
В таком случае модуль этой силы
(Delta F=k I Delta l Bsin{alpha}), ((2))
где (alpha) — угол между направлением вектора (vec{B}) и направлением вектора (vec{Delta l}).
Эту силу, действующую на проводник с током, находящийся в магнитном поле, называют силой Ампера.
Если прямой проводник длиной (l), по которому течёт ток (I), находится в однородном магнитном поле с индукцией (B), то величина силы определится по формуле:
(boxed{F=IBlsin{alpha}.}) ((3))
Рассмотрим два параллельных проводника бесконечной длины, по первому из которых течёт ток величиной (I_1), а по второму — ток (I_2). Пользуясь формулой ((1)) и законом Био — Савара — Лапласа, можно найти величину силы, которая действует на участок второго проводника длиной (l):
(F=frac{mu_0}{4 pi}cdotfrac{2 I_1 I_2}{d}). ((4))
Заметим, что эта сила направлена так, что проводники притягиваются, если ток по ним течёт в одну сторону, а если в противоположные стороны, то проводники отталкиваются.
Сила Лоренца
Пользуясь выражением для силы Ампера, можно найти и силу, которая будет действовать на заряд, движущийся в магнитном поле, — силу Лоренца.
Если представить электрический ток как совокупность (N) заряженных движущихся частиц в кусочке проводника длиной (Delta l), то можно записать
(I=qnvS), ((5))
где (q) — это заряд частиц, (n) — их концентрация, (v) — скорость упорядоченного движения, а (S) — площадь поперечного сечения проводника.
Из закона Ампера с учётом формулы ((3)) следует, что сила, действующая на элемент с током длины (Delta l), определяется по формуле:
(vec{F}=Icdot Delta vec{l} times vec{B}=qnvS cdot vec{Delta l} times vec{B}).
Поскольку векторы скорости (vec{v}) и (vec{Delta l}) сонаправлены, а количество заряженных частиц в рассматриваемом отрезке проводника (N=nS Delta l), то
(vec{F}=qnS Delta l cdot vec{v} times vec{B}=qN cdot vec{v} times vec{B}).
Итого, на каждую движущуюся заряженную частицу действует магнитное поле с силой, называемой силой Лоренца
(boxed{vec{F}=q vec{v} times vec{B}.}) ((6))
Заметим, что сила Лоренца перпендикулярна скорости. Откуда следует, что она перпендикулярна перемещению частицы. Поэтому её работа на любом пути равна нулю.
Величина силы Лоренца определяется выражением
(boxed{F=q v B sin alpha}), ((7))
где (alpha) — угол между вектором (vec{B}) и вектором (vec{v}).
From Wikipedia, the free encyclopedia
This article is about Ampère’s force law. For the law relating the integrated magnetic field around a closed loop to the electric current through the loop, see Ampère’s circuital law.
Two current-carrying wires attract each other magnetically: The bottom wire has current I1, which creates magnetic field B1. The top wire carries a current I2 through the magnetic field B1, so (by the Lorentz force) the wire experiences a force F12. (Not shown is the simultaneous process where the top wire makes a magnetic field which results in a force on the bottom wire.)
In magnetostatics, the force of attraction or repulsion between two current-carrying wires (see first figure below) is often called Ampère’s force law. The physical origin of this force is that each wire generates a magnetic field, following the Biot–Savart law, and the other wire experiences a magnetic force as a consequence, following the Lorentz force law.
Equation[edit]
Special case: Two straight parallel wires[edit]
The best-known and simplest example of Ampère’s force law, which underlaid (before 20 May 2019[1]) the definition of the ampere, the SI unit of current, states that the magnetic force per unit length between two straight parallel conductors is
where 




This is a good approximation if one wire is sufficiently longer than the other, so that it can be approximated as infinitely long, and if the distance between the wires is small compared to their lengths (so that the one infinite-wire approximation holds), but large compared to their diameters (so that they may also be approximated as infinitely thin lines). The value of 

In the SI system,[2][3]
with 
μ0 = 1.25663706212(19)×10−6 H/m
General case[edit]
The general formulation of the magnetic force for arbitrary geometries is based on iterated line integrals and combines the Biot–Savart law and Lorentz force in one equation as shown below.[4][5][6]
where
is the total magnetic force felt by wire 1 due to wire 2 (usually measured in newtons),
and
are the currents running through wires 1 and 2, respectively (usually measured in amperes),
- The double line integration sums the force upon each element of wire 1 due to the magnetic field of each element of wire 2,
and
are infinitesimal vectors associated with wire 1 and wire 2 respectively (usually measured in metres); see line integral for a detailed definition,
- The vector
is the unit vector pointing from the differential element on wire 2 towards the differential element on wire 1, and |r| is the distance separating these elements,
- The multiplication × is a vector cross product,
- The sign of
is relative to the orientation
(for example, if
points in the direction of conventional current, then
).
To determine the force between wires in a material medium, the magnetic constant is replaced by the actual permeability of the medium.
For the case of two separate closed wires, the law can be rewritten in the following equivalent way by expanding the vector triple product and applying Stokes’ theorem:[7]
In this form, it is immediately obvious that the force on wire 1 due to wire 2 is equal and opposite the force on wire 2 due to wire 1, in accordance with Newton’s 3rd law.
Historical background[edit]
Diagram of original Ampere experiment
The form of Ampere’s force law commonly given was derived by Maxwell and is one of several expressions consistent with the original experiments of Ampère and Gauss.
The x-component of the force between two linear currents I and I‘, as depicted in the adjacent diagram, was given by Ampère in 1825 and Gauss in 1833 as follows:[8]
Following Ampère, a number of scientists, including Wilhelm Weber, Rudolf Clausius, James Clerk Maxwell, Bernhard Riemann, Hermann Grassmann,[9] and Walther Ritz, developed this expression to find a fundamental expression of the force. Through differentiation, it can be shown that:
and also the identity:
With these expressions, Ampère’s force law can be expressed as:
Using the identities:
and
Ampère’s results can be expressed in the form:
As Maxwell noted, terms can be added to this expression, which are derivatives of a function Q(r) and, when integrated, cancel each other out. Thus, Maxwell gave «the most general form consistent with the experimental facts» for the force on ds arising from the action of ds‘:[10]
Q is a function of r, according to Maxwell, which «cannot be determined, without assumptions of some kind, from experiments in which the active current forms a closed circuit.» Taking the function Q(r) to be of the form:
We obtain the general expression for the force exerted on ds by ds:
Integrating around s‘ eliminates k and the original expression given by Ampère and Gauss is obtained. Thus, as far as the original Ampère experiments are concerned, the value of k has no significance. Ampère took k=−1; Gauss took k=+1, as did Grassmann and Clausius, although Clausius omitted the S component. In the non-ethereal electron theories, Weber took k=−1 and Riemann took k=+1. Ritz left k undetermined in his theory. If we take k = −1, we obtain the Ampère expression:
If we take k=+1, we obtain
Using the vector identity for the triple cross product, we may express this result as
When integrated around ds‘ the second term is zero, and thus we find the form of Ampère’s force law given by Maxwell:
Derivation of parallel straight wire case from general formula[edit]
Start from the general formula:
Assume wire 2 is along the x-axis, and wire 1 is at y=D, z=0, parallel to the x-axis. Let 




and
Therefore, the integral is
Evaluating the cross-product:
Next, we integrate 


If wire 1 is also infinite, the integral diverges, because the total attractive force between two infinite parallel wires is infinity. In fact, what we really want to know is the attractive force per unit length of wire 1. Therefore, assume wire 1 has a large but finite length 
As expected, the force that the wire feels is proportional to its length. The force per unit length is:
The direction of the force is along the y-axis, representing wire 1 getting pulled towards wire 2 if the currents are parallel, as expected. The magnitude of the force per unit length agrees with the expression for 
Notable derivations of Ampère’s force law[edit]
Chronologically ordered:
- Ampère’s original 1823 derivation:
- Assis, André Koch Torres; Chaib, J. P. M. C; Ampère, André-Marie (2015). Ampère’s electrodynamics: analysis of the meaning and evolution of Ampère’s force between current elements, together with a complete translation of his masterpiece: Theory of electrodynamic phenomena, uniquely deduced from experience (PDF). Montreal: Apeiron. ISBN 978-1-987980-03-5.
- Maxwell’s 1873 derivation:
- Treatise on Electricity and Magnetism vol. 2, part 4, ch. 2 (§§502–527)
- Pierre Duhem’s 1892 derivation:
- Duhem, Pierre Maurice Marie (9 September 2018). Ampère’s Force Law: A Modern Introduction. Alan Aversa (trans.). doi:10.13140/RG.2.2.31100.03206/1. Retrieved 3 July 2019. (EPUB)
- translation of: Leçons sur l’électricité et le magnétisme vol. 3, appendix to book 14, pp. 309-332 (in French)
- Duhem, Pierre Maurice Marie (9 September 2018). Ampère’s Force Law: A Modern Introduction. Alan Aversa (trans.). doi:10.13140/RG.2.2.31100.03206/1. Retrieved 3 July 2019. (EPUB)
- Alfred O’Rahilly’s 1938 derivation:
- Electromagnetic Theory: A Critical Examination of Fundamentals vol. 1, pp. 102–104 (cf. the following pages, too)
See also[edit]
- Ampere
- Magnetic constant
- Lorentz force
- Ampère’s circuital law
- Free space
References and notes[edit]
- ^ «26th CGPM Resolutions» (PDF). BIPM. Retrieved 1 August 2020.
- ^ Raymond A Serway & Jewett JW (2006). Serway’s principles of physics: a calculus based text (Fourth ed.). Belmont, California: Thompson Brooks/Cole. p. 746. ISBN 0-534-49143-X.
- ^ Paul M. S. Monk (2004). Physical chemistry: understanding our chemical world. New York: Chichester: Wiley. p. 16. ISBN 0-471-49181-0.
- ^ The integrand of this expression appears in the official documentation regarding definition of the ampere BIPM SI Units brochure, 8th Edition, p. 105
- ^ Tai L. Chow (2006). Introduction to electromagnetic theory: a modern perspective. Boston: Jones and Bartlett. p. 153. ISBN 0-7637-3827-1.
- ^ Ampère’s Force Law Scroll to section «Integral Equation» for formula.
- ^ Christodoulides, C. (1988). «Comparison of the Ampère and Biot–Savart magnetostatic force laws in their line-current-element forms». American Journal of Physics. 56 (4): 357–362. Bibcode:1988AmJPh..56..357C. doi:10.1119/1.15613.
- ^ O’Rahilly, Alfred (1965). Electromagnetic Theory. Dover. p. 104. (cf. Duhem, P. (1886). «Sur la loi d’Ampère». J. Phys. Theor. Appl. 5 (1): 26–29. doi:10.1051/jphystap:01886005002601. Retrieved 7 January 2015., which appears in Duhem, Pierre Maurice Marie (1891). Leçons sur l’électricité et le magnétisme. Vol. 3. Paris: Gauthier-Villars.)
- ^ Petsche, Hans-Joachim (2009). Hermann Graßmann : biography. Basel Boston: Birkhäuser. p. 39. ISBN 9783764388591.
- ^ Maxwell, James Clerk (1904). Treatise on Electricity and Magnetism. Oxford. p. 173.
External links[edit]
- Ampère’s force law Includes animated graphic of the force vectors.

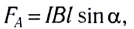
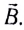

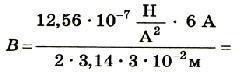
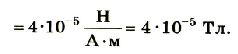
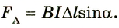
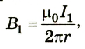
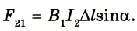
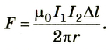
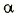 = 30%
= 30%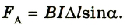
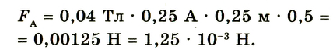
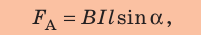
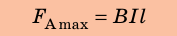
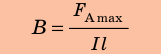
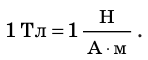
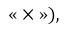
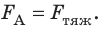
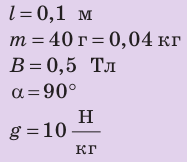

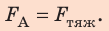
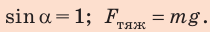
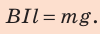
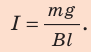
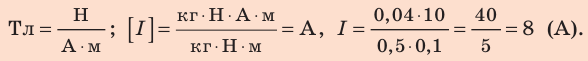

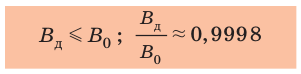

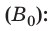

























![{displaystyle d^{2}F_{x}=kII'dsds'{frac {1}{r^{2}}}left[left(left({frac {partial r}{partial s}}{frac {partial r}{partial s'}}-2r{frac {partial ^{2}r}{partial spartial s'}}right)+r{frac {partial ^{2}Q}{partial spartial s'}}right)cos(rx)+{frac {partial Q}{partial s'}}cos(x,ds)-{frac {partial Q}{partial s}}cos(x,ds')right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21804ef28aa3fd9e5a24bc0170094b6bcee2f81c)

![{displaystyle d^{2}mathbf {F} =-{frac {kII'}{2r^{2}}}left[left(3-kright){hat {mathbf {r} }}_{1}left(dmathbf {s} ,dmathbf {s} 'right)-3left(1-kright){hat {mathbf {r} }}_{1}left(mathbf {hat {r}} _{1}dmathbf {s} right)left(mathbf {hat {r}} _{1}dmathbf {s} 'right)-left(1+kright)dmathbf {s} left(mathbf {hat {r}} _{1}dmathbf {s} 'right)-left(1+kright)dmathbf {s} 'left(mathbf {hat {r}} _{1}dmathbf {s} right)right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fb00c2f89f81151847b22559e064c5afcd09a08)
![{displaystyle d^{2}mathbf {F} =-{frac {kII'}{r^{3}}}left[2mathbf {r} (dmathbf {s} ,dmathbf {s'} )-3mathbf {r} (mathbf {r} dmathbf {s} )(mathbf {r} dmathbf {s'} )right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f7c536b3686110843ed9be4d2c355589b4f6b19)
![{displaystyle d^{2}mathbf {F} =-{frac {kII'}{r^{3}}}left[mathbf {r} left(dmathbf {s} ,dmathbf {s'} right)-dmathbf {s} left(mathbf {r} ,dmathbf {s} 'right)-dmathbf {s} 'left(mathbf {r} ,dmathbf {s} right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23e5ed6b901c403ab24fb2ccdca3c137dce75650)
![{displaystyle d^{2}mathbf {F} ={frac {kII'}{r^{3}}}left[left(dmathbf {s} times dmathbf {s'} times mathbf {r} right)+dmathbf {s} '(mathbf {r} ,dmathbf {s} )right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c1ded6be0aeb12d95a4cf21b8b8fdb439432db8)



![{displaystyle mathbf {F} _{12}={frac {mu _{0}I_{1}I_{2}}{4pi }}int _{L_{1}}int _{L_{2}}{frac {(dx_{1},0,0) times left[(dx_{2},0,0) times (x_{1}-x_{2},D,0)right]}{|(x_{1}-x_{2})^{2}+D^{2}|^{3/2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fed1cecb00df0ba2b78c57f8029341ca89cbd7a)



