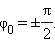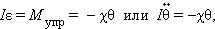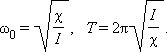Содержание:
- Законы динамики
- Первый закон или закон инерции
- Второй закон или основной закон динамики
- Третий закон или закон равенства действия и противодействия
- Четвертый закон или закон независимости действия сил
- Прямая (основная) задача динамики
- Порядок решения прямой задачи динамики материальной точки
- Примеры решения задач
- Задания темы Д1
- Пример решения задания Д1а
- Задания Д1б
- Пример решения задания Д1б
- Обратная задача динамики и её решение
- Порядок решения обратной задачи динамики материальной точки
- Примеры решения задач
- Задания темы Д2
- Пример решения задачи темы Д2
- Колебания и динамика относительного движения материальной точки
- Колебания материальной точки
- Фаза вынужденных колебаний
- Амплитуда вынужденных колебаний
- Явление резонанса
- Порядок решения задач на колебательное движение материальной точки
- Примеры решения задач
- Сжатые сведения по теории динамики относительного движения материальной точки
- Переносная сила инерции
- Порядок решения задач динамики относительного движения материальной точки
- Примеры решения задач
- Задания темы Д3
- Пример решения темы Д3
- Теоремы о движении центра масс и об изменении количества движения механической системы
- Порядок решения задач на применение теоремы о движении центра масс
- Примеры решения задач
- Теоремы об изменении количества движения материальной точки и механической системы
- Порядок решения задач на применение теоремы об изменении количества движения точки и механической системы
- Примеры решения задач
- Задания темы Д4
- Пример решения темы Д4
- Теорема о смене кинетической энергии механической системы
- Теорема об изменении кинетической энергии материальной точки в интегральной форме
- Порядок решения задач на применение теоремы об изменении кинетической энергии в интегральной форме
- Примеры решения задач
- Задания темы Д5
- Пример решения темы Д5
- Принцип даламбера
- Принцип Даламбера для материальной точки
- Принцип Даламбера для механической системы
- Приведение сил инерции точек твердого тела к простому виду
- Порядок решения задач на применение принципа Даламбера
- Примеры решения задач
- Задание темы Д6
- Пример решения темы Д6
- Дополнительные лекции и примеры по теме «Динамика»
- Законы динамики, уравнения движения материальной точки. принцип даламбера
- Пример решения задачи 1.14
- Принцип ДАламбера
- Силы, действующие на точки механической системы
- Теорема о движении центра масс механической системы
- Пример решения задачи 1.15.
- Краткие исторические сведения о динамике
- Динамика и ее основные задачи
- Законы Ньютона
- Первый закон Ньютона (закон инерции)
- Второй закон Ньютона (основной закон динамики)
- Третий закон Ньютона (закон равенства действия и противодействия}
- Дифференциальные уравнения движения свободной материальной точки
- Две основные задачи динамики свободной материальной точки
- Прямая или первая, основная задача
- Обратная, или вторая, основная задача
- Уравнения движения несвободной материальной точки
- Движение точки по гладкой неподвижной поверхности
- Движение точки по гладкой неподвижной кривой
- Натуральные уравнения движения по кривой
Динамика – это раздел теоретической механики, в котором изучается движение материальных тел под действием приложенных к ним сил. Покой – частный случай движения, поэтому раздел статики – это частный случай динамики.
В лекции кроме минимума теоретических знаний, какими должен овладеть студент по динамике, приводятся примеры решения различных задач, исходные данные к индивидуальному расчетно-графическому заданию и образец его выполнения.
Задачи расчетно-графического задания охватывают материалы следующих тем динамики:
— прямая задача динамики материальной точки (тема Д1);
— обратная задача динамики материальной точки (тема Д2);
— колебания и динамики относительного движения материальной точки (тема Д3);
— теоремы о движении центра масс и об изменении количества движения механической системы (тема Д4);
— теорема об изменении кинетической энергии механической системы (тема Д5);
— принцип Даламбера (тема Д6).
Вариант расчетно-графического задания определяется двумя цифрами, которые представляют собой две последние цифры номера зачетной книжки или задаются преподавателем. Первая цифра определяет номер рисунка, а вторая — номер варианта в таблице.
Законы динамики
Динамика — раздел теоретической механики, в котором изучается механическое движение материальных тел (точек) с учетом причин, которые вызывают или меняют это движение, то есть с учетом масс тел и сил, которые действуют на них.
В основе динамики лежат законы Ньютона, которые следуют из обобщения большого количества опытных фактов. Приведем основные законы динамики в современном преподавании.
Первый закон или закон инерции
Материальная точка, на которую не действует сила 
движения относительно инерциальной системы отсчета:
где 

Такое движение называется движением по инерции или движение без ускорения. Из закона следует, что для изменения скорости точки, то есть придание ей ускорения, необходимо подействовать на нее силой, отличной от нуля. Справедливо и обратно,
если материальная точка движется неравномерно или непрямолинейно, то она движется с ускорением, то есть на нее действует сила.
Инерциальной системой отсчета называется такая система, в которой выполняются первый и второй основные законы механики.
Неинерциальной системой отсчета называется такая система, которая движется с ускорением относительно инерциальной. В неинерциальной системе отсчета первый и второй законы динамики не выполняются.
Второй закон или основной закон динамики
Ускорение, которое приобретает материальная точка под действием силы, имеет направление силы, прямо пропорциональное силе и обратно пропорциональное массе точки.
Или эквивалентное определение: сила, действующая на материальную точку, равна произведению массы точки на ее ускорение и имеет направление ускорения

Масса «m» является положительная скалярная величина, которая характеризует степень сопротивления материальной точки изменению ее скорости, то есть является мерой инертности точки. В классической механике считается, что масса материальной точки есть величина постоянная.
За единицу массы в системе СИ принято килограмм:
Третий закон или закон равенства действия и противодействия
Силы, с которыми две материальные точки действуют друг на друга, равны по величине и направлены в противоположные стороны вдоль прямой, которая соединяет эти точки, то есть
где 

Если одну из этих сил назвать «действием», то вторая будет «противодействием». Если одну силу назвать «активной силой», то вторая будет «реакцией». Таким образом, при взаимодействии двух материальных точек силы всегда появляются парами и являются силами одной природы. Это означает, что ускорение, которые приобретают материальные точки под действием сил взаимодействия, обратно пропорциональные их массам.
Следует помнить, что эти силы приложены к разным материальным точкам и поэтому не уравновешивают друг друга.
Четвертый закон или закон независимости действия сил
Ускорение, которое приобретает материальная точка при одновременном действии на нее нескольких сил, равно векторной сумме ускорений, которые приобретает материальная точка под действием каждой из сил в отсутствии
других сил, то есть
Закон утверждает, что силы, которые одновременно действуют на
материальную точку, не влияют друг на друга и поэтому подлежат принципу суперпозиции (наложения) сил. Это значит, что одновременное действие на материальную точку системы сил 
которая называется равнодействующей и равной векторной сумме сил,которые
действуют:
Силы прибавляемых называются составляющими или компонентами равнодействующей. Сложение сил выполняется за правилом параллелограмма или его модификациями (правилами треугольника, или силового многоугольника).
Таким образом, если на материальную точку одновременно действуют несколько сил, то в уравнениях (1) и (2) под силой 

Дифференциальное уравнение движения материальной точки (2) в векторной форме выглядит:
или в сокращенной форме записи
где

Уравнение (6) представляет собой математическое выражение основного закона динамики (2) в векторной форме.
В зависимости от характера и постановки конкретной задачи это уравнение часто используют в скалярной форме, то есть в проекциях на оси любой системы координат.
Дифференциальные уравнения движения материальной точки в проекциях на оси 
или
где, 




Дифференциальные уравнения движения материальной точки в
проекциях на оси 
имеют вид:
или
где 









Как следует из (8), проекция на бинормаль равнодействующей сил, приложенных к материальной точке, равно нулю. Это означает, что траектория точки расположена так, что равнодействующая сила всегда лежит в плоскости 
С помощью дифференциальных уравнений движения материальной точки 
Первой, или прямой задачей динамики называется задача, в которой по заданному закону движения и массе материальной точки определяется равнодействующая сил, которые приложены к точке.
Второй, либо обратной, либо основной задачей динамики называется задача, в которой по заданным силам, что действуют на материальную точку, массе точки и начальным
условиям определяется закон движения материальной точки.
Прямая (основная) задача динамики
Краткие сведения по теории:
Задача Д1 — на решение первой (прямой) задачи динамики материальной точки.
Если необходимо определить равнодействующую 


или 




на соответствующие оси координат. Тогда величина равнодействующей вычисляется по
формулами:

Направление вектора 
— или по значению косинусов направляющих углов между


осей координат 

— или по значению тангенса угла между вектором
и единичным вектором 
Порядок решения прямой задачи динамики материальной точки
Если в задаче необходимо определить любую из составляющих равнодействующей или другой величины, то рекомендуется следующий порядок решения:
1. Изобразить на рисунке материальную точку в произвольном положении.
2. Показать активные силы и реакции связей, что на нее действуют.
3. Выбрать систему отсчета.
4. Записать векторное уравнение движения точки в форме второго закона динамики.
5. Спроектировать векторное уравнение движения точки на выбранные оси координат.
6. Из полученных уравнений определить необходимые величины.
Примеры решения задач
Задача 1
Пуля весом 


Определить силу сопротивления окружения R в виде функции
скорости, то есть
Решение. Изобразим шар в произвольном положении на траектории и покажем силы, которые на него действуют
(рис.1.3): 

Движение шара происходит вдоль вертикали, поэтому направим ось 

Запишем уравнение движения пули в векторной форме:
и спроектируем его на ось
откуда
Таким образом, чтобы определить силу сопротивления R, необходимо знать ускорение шара
Поскольку закон изменения координаты 
Находим первую и вторую производные от закона движения
пули:
Таким образом,
Из выражения для 

то есть
Ответ:
Задача 2
Движение тела А массой 
где 

Определить силу 
(Рисс.1).
Решение. Проекции на оси координат силы 
где 

В данном случае
Итак
Модуль 
Сила 


Ответ:
Задача 3
Материальная точка массой 

Определить модуль R равнодействующей силы, которые приложенные к материальной точке.
Решение. В задаче движение материальной точки задано естественным способом, поэтому для определения равнодействующей сил воспользуемся зависимостями (8):
Определим касательное и нормальное ускорение материальной точки:
Поскольку 

касательную ось равняется нулю.
Находим нормальную составляющую равнодействующей сил:
Модуль равнодействующей определим из выражения (Д1.1):
Таким образом, заданное движение материальной точки происходит под действием силы, постоянной по модулю и направленной вдоль радиуса к центру круга.
Ответ:
Задача 4
Материальная точка массой 

Определить проекцию 
Решение. Для определения проекции 
Сначала найдем значение скорости материальной точки:
Определяем величину касательного ускорения
Подставив в уравнение (1) значение 

Ответ:
Задача 5
Груз M весом 

горизонтальной плоскости, при этом нить с вертикалью образует угол
Определить величину скорости груза V и модуль силы натяжения нити T.
Решение. Изобразим груз M в произвольном положении и покажем силы, которые на него действуют: силу притяжения 

Для решения задачи выбираем естественную систему координат: ось 

центра кривизны и ось 
Запишем уравнение движения груза в векторной форме:
Проектируем это векторное уравнение на оси координат:
Модуль силы натяжения нити T найдем из третьего из уравнений (1), учитывая, что
Из второго из уравнений (1) найдем V, если учесть, что
то
Откуда
Ответ:
Задания темы Д1
Д1.5. Задача Д1
Указания. Задание Д1 содержит две задачи Д1а и Д1б, которые надо решить. Обе задачи являются прямыми или первыми задачами динамики материальной точки. Отличие заключается в том, что при решении задачи Д1а надо воспользоваться дифференциальными уравнениями движения точки в проекциях на оси декартовой системы координат, а при решении задачи Д1б — в проекциях на природные оси координат.
Следует помнить, что направление вектора силы совпадает с направлением вектора соответствующего ускорения.
Д1.6. Задача Д1а
Материальная точка М массой m движется в пространстве
в соответствии с уравнениями:



Зависимости 


времени 
Определить величину и направление равнодействующей системы сил, действующих на материальную точку в момент времени
Примечание. Первая цифра шифра определяет номер рисунка, а вторая — номер варианта в таблице.
Пример решения задания Д1а
Дано:
Определить: равнодействующую
Решение. Поскольку кинематические уравнения движения материальной точки заданы координатным способом, то воспользуемся дифференциальными уравнениями движения точки в проекциях на оси декартовой системы координат:
где,

Поскольку 
Дважды дифференцируем по времени заданные кинематические уравнения движения:
и подставляем полученные выражения в (2). С учетом того, что 
или
В заданный момент
Тогда модуль равнодействующей силы:
Ориентация в пространстве вектора равнодействующей определяется направляющими углами 



Эти углы находятся по значениям их косинусов:
Ответ:
Задания Д1б
Материальное тело М массой m скользит (коэффициент трение скольжения 
рис, Д1.2. Уравнение движения тела 

В момент времени 




Найти. Считая тело материальной точкой определить в моменты времени 


Пример решения задания Д1б
Дано: траектория точки (рис. Д1.3),
Определить: величину и направление силы 

Решение.
1. Изобразим тело (материальную точку) в положении 
Покажем силы, которые действуют на материальную точку: 



Поскольку траектория точки известна, свяжем с ней естественную систему координат 


Запишем уравнение движения материальной точки в векторной форме:
Проектируем это векторное уравнение на оси выбранной системы координат:
где 



В уравнениях (1) и (2):
где 
Скорость точки равна:
Тогда:
В положении точки 

Поскольку 

Тогда
Уравнение (1) решим относительно силы
Таким образом, в этом положении материальной точки сила 
2. Изобразим материальную точку в положении 
угол
Покажем силы, которые на нее действуют: 



Покажем выбранную систему координат в этом положении точки (ось 
по касательной к траектории в сторону движения точки, а ось 

Запишем уравнение движения материальной точки в векторной форме:
Проектируем это векторное уравнение на оси выбранной системы координат:
В положении точки 
Из уравнения (6) определим величину нормальной реакции 
Тогда, сила трения равна:
Уравнение (5) решим относительно силы

Таким образом, в этом положении материальной точки сила
направлена против направления ее движения (поскольку величина силы отрицательная).
Ответ:
Обратная задача динамики и её решение
Краткие сведения по теории:
Задача Д2 — на решение второй (обратной или основной) задачи динамики материальной точки. Для её решение необходимо проинтегрировать или дифференциальное уравнение движения материальной точки в векторной форме, или равносильные ему системы скалярных уравнений, которые соответствуют выбранной системе отсчета, с учетом начальных условий.
Если, например, задача решается в проекциях на оси декартовой системы координат, то интегрируется система дифференциальных уравнений второго порядка:
При интегрировании каждого из этих уравнений появится
по две постоянные произвольные интегрирования, а всего их будет шесть, и
общее решение уровней движения точки будет иметь вид:
где 
Чтобы получить частичное решение уравнений движения точки, которое будет соответствовать ее действительному движению, необходимо определить значение постоянных произвольных . Для этого необходимы дополнительные данные, которые определяют положение точки и ее скорость в некоторый фиксированный момент времени t. Если 
Положение точки определяется тремя ее декартовыми координатами 

системы дифференциальных уравнений (Д2.1) при 
В результате подстановки первоначальных условий в первые и вторые интегралы системы (2.1) образуется система шести уравнений для определения шести неизвестных
При движении точки в плоскости, например 

При прямолинейном движении точки, например вдоль оси 

Если задача решается в проекциях на оси природной системы координат, то интегрировать необходимо дифференциальные уравнения движения для этой системы координат:
Начальными условиями в этом случае будут значение дуговой координаты S и проекция вектора скорости на направление касательной траектории 
Наконец, заметим, что заданная начальная скорость движения точки учитывает влияние на ее движение тех сил, которые действовали на точку до начального момента времени.
Порядок решения обратной задачи динамики материальной точки
Обратные задачи динамики материальной точки рекомендуется решать следующим образом:
1. Изобразить на рисунке материальную точку в произвольном положении и все силы, которые на нее действуют (как активные, так и реакции связей).
2. Выбрать систему отсчета, в которой задача решается наиболее простым способом. При этом начало координат расположить в месте, где находилась точка в начальный момент времени
3. Сохранить исходные условия задачи.
4. Составить дифференциальное уравнение движения точки в проекциях на оси системы координат, которая выбрана.
5. Провести интегрирование полученной системы дифференциальных уравнений движения точки.
6. Определить по первоначальным условиям постоянные интегрирования.
7. Из полученной системы уравнений определить неизвестные величины.
Примеры решения задач
Задача 1
Тяжелое тело скользит по гладкой поверхности, которая наклонена под углом
к горизонту.
Определить, за какое время Т тело пройдет путь 
момент его скорость равнялась
Решение. Представим тело в произвольном положении на наклонной плоскости (рис.1). Поскольку движение тела по плоскости является поступательным, а при поступательном движении ускорения всех точек тела одинаковые, то движение такого тела будем рассматривать как движение материальной точки (данное допущение
будет справедливым и для следующих задач этой темы).
Покажем силы, которые действуют на тело: силу притяжения 
Ось 
В начальный момент времени 


Запишем уравнение движения тела в векторной форме:
Спроектируем записанное уравнение на ось
Учитывая, что 
Найдем зависимость скорости 
Используя начальные условия, определим постоянное положение
интегрирования 

Таким образом, уравнение для изменения скорости материальной точки будет иметь вид:
Находим зависимость координаты 
Постоянное интегрирование 

Окончательно, для координаты 
Определим время Т, при котором
или
Отсюда:
Поскольку время может быть только положительным, то:
Ответ:
Задача 2
Тяжелое тело поднимается по негладкой наклонной плоскости, которая наклонена к горизонту под углом 

Определить, какой путь S пройдет тело до остановки? За какое время Т тело пройдет этот путь?
Решение. Изобразим тело в виде материальной точки в произвольном положении (рис.1).
Покажем силы, которые действуют на материальную точку: силу притяжения 

Ось 



Запишем уравнение движения точки в векторной форме:
Проектируем векторное уравнение (1) на оси координат:
Поскольку точка в направлении оси 

Подставив в уравнение (2) 
где
Тогда
или
После интегрирования этого уравнения получим:
Соотношение (4) является первым интегралом дифференциального уравнения (2). Для определения постоянной интегрирования 
Тогда:
Для определения закона движения точки запишем полученное уравнение следующим образом:
Разделим переменные и проинтегрируем выражение:
Постоянная интегрирования 

Таким образом, закон движения тела выглядит:
Итак, мы получили законы изменения скорости (5) и координаты 
Определим время Т движения тела до полной остановки, скорость при этом будет равна нулю. Подставим 
откуда:
Через время Т, согласно уравнению (6), точка будет находиться от начала координат на расстоянии S, которое в нашем случае численно равно пройденному точкой пути:
Подставив выражение для Т, получим:
С учетом числовых значений получим:
Ответ:
Задача 3
Точка М, масса которой m, движется под действием силы притяжения по гладенькой внутренней поверхности желоба (рис.1). Поверхность желоба представляет собой часть боковой поверхности цилиндра радиусом r. В начальный момент времени точка
находится в положении 
Определить скорость V точки М и реакцию T поверхности желоба в положении, когда центральный угол
Решение. Изобразим точку М в произвольном положении на траектории, которой является внутренняя поверхность желоба. Положение точки определяется углом
Покажем силы, которые действуют на точку М: 

Поскольку траектория точки известна (дуга с радиусом r), то свяжем с точкой М естественную систему координат
Уравнение движения точки М в векторной форме имеет вид:
Спроектируем векторное уравнение (1) на координатные
оси:
то есть
В уравнениях (2) и (3) три переменные величины: 
выражаем в уравнении (2) переменную t через переменную
Поскольку 
Разделим переменные в последнем уравнении и проинтегрируем:
Поскольку при 


Таким образом, закон изменения скорости материальной точки будет иметь вид:
В положении, когда 
После определения скорости точки М из уравнения (3) находим нормальную реакцию внутренней поверхности цилиндра:
При 

Ответ:
Задача 4
Тяжелое кольцо М нанизано на горизонтальный гладкий проволочный круг (рис. 1). Кольцу придают начальную скорость 

Определить: через какой промежуток времени 
Решение. Поскольку траектория тяжелого кольца М известна — это круг радиуса r, то с кольцом повяжем естественную систему координат
Покажем силы, действующие на тяжелое кольцо М: 



Уравнение движения кольца М в векторной форме имеет вид:
Спроектируем это уравнение на ось

Разделим в последнем уравнении переменные и проинтегрируем. При интегрировании учтем, что скорость кольца меняется от 

Таким образом, закон изменения скорости тяжелого кольца будет иметь вид:
Определим время движения кольца. В момент времени
когда кольцо останавливается, скорость 
Подставив в последнее уравнение числовые данные, получим:
Ответ:
Задания темы Д2
Груз М массой m, получив в точке А начальную скорость 
На участке АВ на груз, кроме силы притяжения 


В точке В груз, не меняя значения своей скорости, переходит на участок трубы ВС, где на него, кроме силы притяжения 





Найти закон движения груза на участке ВС, то есть 



Указания. Задача Д2 является второй или обратной задачей динамики точки, которая решается путем составления и следующего двукратного интегрирования дифференциального уравнения второго порядка с учетом первоначальных условий. При этом следует помнить, что если в какой-то момент времени силы, которые действуют на материальную точку, меняются, то для описания следующего движения точки необходимо составить и интегрировать новое дифференциальное уравнение ее движения. Начальными условиями нового движения точки будут ее положение и скорость в конце предыдущего движения.
В случае, если задана длина 

Пример решения задачи темы Д2
Дано:
Определить: 

Решение. Поскольку силы, которые действуют на груз, в точке В меняются, то решение задачи разбивается на две части. Сначала рассматривается движение груза на участке АВ, а затем на участке ВС.
1. Рассмотрим движение груза на участке АВ (рис. Д 2.2), считая его материальной точкой
Изобразим груз в произвольном положении 




Начало прямоугольной системы координат 

Запишем основное уравнение динамики в векторном виде и в проекциях на ось
Учитывая, что:
уравнение (2) приобретает вид:
Поделив на m и подставив числовые значения, получим:
Поскольку по условию задачи надо определить скорость тела в зависимости от пройденного расстояния 
Разделим переменные в уравнении (3), преобразуем к виду, удобному для интегрирования, и проинтегрируем:
По исходным условиям 
Тогда уравнение (4) приобретет вид:
откуда мы находим выражение для V:
Считая в уравнении 

Эта скорость будет начальной скоростью движения груза на участке ВС.
2. Рассмотрим движение груза на участке ВС. Изобразим груз (рис. Д2.2) в произвольном положении 
сила притяжения; 


Выберем систему координат для этого участка. Начало прямоугольной системы координат 
принимаем направление движения груза.
Запишем основное уравнение динамики в векторном виде и в проекциях на ось
Учитывая, что
уравнение (6) приобретает вид:
Поделив на m и подставив числовые значения 

Разделим переменные и проинтегрируем уравнение (7). Интегрирование выполняется с помощью определенных интегралов, верхняя граница которых переменная. При этом нижней границей будут первоначальные условия. При изменении времени от
к t скорость точки меняется от 

Учитывая, что 
Рассмотрим переменные и интегрируем:
Ответ: закон движения груза на участке BC:
где 

Колебания и динамика относительного движения материальной точки
Краткие сведения по теории колебаний материальной точки:
Задача Д3 охватывает одновременно колебания и динамику относительного движения материальной точки.
Колебания материальной точки
Механическими периодическими колебаниями называют такие движения материальной точки, при которых она по очереди перемещается в двух противоположных направлениях относительно положения равновесия, и которые повторяются через определенные промежутки времени.
Основными характеристиками периодических колебаний являются период и частота.
Периодом колебаний (Т) называется наименьший промежуток времени, после которого повторяются значения величин, характеризующих колебательную систему и меняются при колебаниях.
За период колебаний система осуществляет одно полное колебание.
Единицей периода в системе СИ является секунда:
Частотой колебаний (v) называется величина, которая обратная периоду и равна числу полных колебаний в секунду,
Единицей частоты в системе СИ является Герц (Гц):
Круговой, или цикличной, или угловой частотой (k) называется величина, которая равна числу полных колебаний за 

Единицей круговой частоты в системе СИ является радиан в секунду:
Наиболее важной разновидностью периодических колебаний являются гармонические колебания.
Гармоническими колебаниями называются такие периодические колебания, при которых величины, которые их характеризуют, меняются по времени по закону синуса или косинуса.
Необходимым условием возникновения колебаний является действие в произвольный момент времени на материальную точку, которая выведена из положение равновесия, восстановительной силы 
Кроме восстановительной силы на материальную точку, которая осуществляет колебания, действуют и другие силы. В зависимости от характера этих сил принято различать свободные, свободные затухающие и вынужденные колебания материальной точки.
Дальнейшее рассмотрение проведем на примере упругого маятника (пружины, к одному концу которой прикреплено тело массой m, а второй конец закреплен, причем массой пружины по сравнению с массой тела пренебрегают), который находится на гладкой горизонтальной поверхности.
Таким образом, исследование колебаний сводится к решению оборотной задачи динамики материальной точки (тела) М, которая движется вдоль горизонтальной оси, например 
Начало отсчета точку О расположим в месте, где находится точка (тело) М при недеформированной пружине. Восстановительная сила во всех случаях будет силой упругости деформированной пружины, которая равна:
где 

и 
Свободными колебаниями материальной точки называются такие ее колебания, которые происходят под действием только восстановительной силы (рис. Д3.1).
В этом случае дифференциальное уравнение движения точки имеет вид:
где 
Период колебаний равен
Решение однородного линейного дифференциального уравнения второго порядка с устойчивыми коэффициентами (Д3.3) или, что тоже самое, закон движения точки выглядит:
где 

Если исходные условия при 



В амплитудной форме записи решение имеет вид:
где 




Амплитуда и начальная фаза колебаний определяются по первоначальным условиям.
Если исходные условия имеют при 


Таким образом, в этом случае материальная точка будет осуществлять незатухающие гармонические колебания, график которых при 
Если на материальную точку кроме восстановительной силы будет действовать постоянная по величине и направлению сила




Свободными затухающими колебаниями материальной точки называются такие ее колебания, которые происходят под действием восстановительной силы 
сопротивления среды 
Пусть сила сопротивления 


где 

Решение этого однородного линейного дифференциального уравнения второго порядка с устойчивыми коэффициентами зависит от соотношения между b и k.
При малом сопротивлении 
или в амплитудной форме
В этих уравнениях 


Тогда условный период 
Как видно из (Д3.12), движение точки носит колебательный характер, потому что координата 

В случаях большого сопротивления 
сопротивления 
точки не входят знакопеременные периодические функции и поэтому движение
точки не будет колебательным. Такое движение называется апериодическим (непериодическим).
Если 
где
Если b = k, то решение уравнения (Д3.10) имеет вид:
Вынужденными колебаниями материальной точки без учета силы сопротивления среды называются такие колебания, которые происходят под действием восстановительной силы 

Пусть проекция вынуждающей силы на ось, совпадающая с направлением движения точки, меняется по закону:
где H — максимальное значение вынужденной силы;
p — частота изменения вынужденной силы;


Дифференциальное уравнение движения точки М в проекции на ось 
или
Если выбрано
то получим дифференциальное уравнение вынужденных колебаний материальной точки:
Решение уравнения (3.18) в амплитудной форме, то есть, зависимость координаты 
где A — амплитуда вынужденных колебаний имеет вид:
Из уравнения (3.19) следует, что движение точки представляет собой наложение двух колебательных движений.
Колебания, которые определяются первым слагаемым:
имеют частоту k свободных гармонических колебаний и называются собственными колебаниями материальной точки.
Колебания, определяемые вторым слагаемым
имеют частоту 

Таким образом, при одновременном действии восстанавливающей и вынуждающей сил точка осуществляет сложное колебательное движение, которое представляет собой результат наложения свободных и вынужденных колебаний точки.
Необходимо подчеркнуть, что частота 

Вынужденные колебания, частота которых меньше частоты свободных колебаний точки, называют вынужденными колебаниями малой частоты.
Вынужденные колебания, частота которых больше частоты свободных колебаний, называют вынужденными колебаниями большой частоты.
Фаза вынужденных колебаний
Если 

Если вынужденные колебания происходят с большой
частотой 

При этом, фаза вынужденных колебаний большой частоты равна 


В случае вынужденных колебаний малой частоты точка М всегда отклонена от начала координат О в ту сторону, в которую направлена в данный момент вынужденная сила 
Амплитуда вынужденных колебаний
Статичным отклонением точки называется величина 
Отсюда
где H — максимальное значение вынужденной силы.
Отношение амплитуды вынужденных колебаний А до статического отклонения 
При
При
График изменения коэффициента динамичности в зависимости от смены частоты вынуждающей силы (рис.Д3.7) имеет разрыв при значении 

Явление резонанса
Явление резонанса возникает когда частоты вынужденных и свободных
колебаний точки совпадают, то есть:
При этом амплитуда А вынужденных колебаний точки равна бесконечности и большинство уравнений вынужденных колебаний, полученных при условии 
Дифференциальное уравнение движения при 
Уравнение (Д3.25) отличается от уравнения (Д3.18) тем, что в правой части стоит частота k, равная частоте собственных колебаний точки.
Решение дифференциального уравнения (Д3.25) имеет вид:
При резонансе частота и период вынужденных колебаний равны, соответственно, частоте k и периоду Т свободных колебаний точки, а фаза вынужденных колебаний 

График отклонений для вынужденных колебаний во время резонанса — это периодическая кривая, напоминающая синусоиду (рис.Д3.8), которая вписывается в область, ограниченную прямыми



Из графика видно, что амплитуды колебаний увеличиваются со временем.
Порядок решения задач на колебательное движение материальной точки
При решении задач на колебания материальной точки рекомендуется придерживаться следующего порядка:
1. Изобразить материальную точку в произвольном положении и показать силы, которые на нее действуют.
2. Выбрать систему отсчета, начало системы координат разместить в положении статического равновесия и направить ось в сторону движения точки.
3. Записать начальные условия движения точки.
4. Составить дифференциальное уравнение движения материальной точки в проекциях на соответствующую ось.
5. Проинтегрировать дифференциальное уравнение движения.
6. Использовать начальные условия определения постоянной интегрирования.
7. Записать окончательное уравнение движения.
Для определения круговой частоты k и 




Рассматривая задачу на свободные колебания материальной точки при отсутствии сил сопротивления, можно доказать решение к результату в общем виде, а уже потом подставить в него многочисленные данные.
Рассматривая же задачу на свободные колебания материальной точки при наличии сил сопротивления, пропорциональных скорости, многочисленные данные надо подставить в составленное дифференциальное уравнение движения и определить величины коэффициентов b и k, поскольку решение дифференциального уравнения движения при таких колебаниях зависит от соотношения этих коэффициентов (случаи малого сопротивления 

Решая задачу на вынужденные колебания надо определять числовые значения коэффициентов дифференциального уравнения, поскольку вид частичного решения этого уравнения зависит от соотношения коэффициентов р и k.
При решении задач, в которых необходимо определить условия, обеспечивающие попадание материальной точки в резонанс, не нужно интегрировать дифференциальные уравнения движения. Для определения этих условий достаточно, воспользовавшись
составленным дифференциальным уравнением движения, определить
круговые частоты свободных — k и вынужденных р колебаний и
сравнять их между собой.
Примеры решения задач
Задача 1
Определить максимальное удлинение 
до недеформированной пружины и отпущен из состояния покоя. Статическая деформация пружины под действием груза равна
Решение. Изобразим груз в произвольном положении (рис.1, б) и покажем силы, которые на него действуют: силу упругости пружины 
Поскольку на груз помимо восстановительной силы 



Когда груз будет находиться в крайнем нижнем положении (рис.1, б), то максимальное удлинение пружины будет состоять из статической деформации 

Величину амплитуды можно определить из выражения:
где 

По условию задачи при
Подставляя значение 

Таким образом, максимальное удлинение пружины равняется:
Ответ:
Задача 2
Определить эквивалентный коэффициент жесткости 
последовательно (рис. 1, а) и параллельно (рис. 2). Коэффициенты жесткости пружин:
Решение: В случае последовательного соединения пружин общее статическое удлинение 
Поскольку каждая из пружин в статическом положении растягивается силой P, то согласно (Д3.9):
С учетом последних соотношений формула (1) имеет вид:
Для эквивалентной расчетной схемы с одной пружиной (рис. 1, б):
где 
Поскольку статическое удлинение указанной (рис. 1, а) и эквивалентной (рис. 1, б) схем должно быть равным, то:
С учетом числовых данных:
Период колебаний по формуле (Д3.9):
В случае параллельного соединения пружин (рис. 2) их статическое удлинение будет одинаковым:
Исходя из формулы (Д3.9) пружины будут растянуты усилиями:
Таким образом, сила притяжения груза P будет уравновешиваться двумя вертикальными усилиями 


С другой стороны, для эквивалентной расчетной схемы с одной пружиной (рис. 1, б):
где
Откуда
С учетом числовых данных:
Период колебаний по формуле (Д3.9):
Ответ:
Задача 3
Дифференциальное уравнение движения материальной точки имеет вид:
Определить максимальное значение массы точки при котором движение будет апериодическим.
Решение. Движение точки будет апериодическим, если выполняется условие
где


Дифференциальное уравнение 
Отсюда:
С учетом полученных значений b и k, условие (1) имеет вид:
Решаем неравенство (2) относительно массы m:
Ответ: максимальное значение массы
Задача 4
Тело весом 





Определить уравнение движения тела
Решение. Перед тем, как записать общее уравнение движения точки, необходимо выяснить, при каком сопротивлении происходит движение, то есть сравнить значение коэффициента b и круговой частоты k:
Из условия задачи следует:
Таким образом, 
В этом случае закон движения точки определяется зависимостью (Д3.16):
Начальные условия: 
Ответ:
Найдя по формуле (2) значение 

Из графика видно, что при 


Моменты времени, в которые груз находится в положении статического равновесия, определяются из уравнений:

Из первого уравнения следует:
Из второго уравнения:
Значение 

Задача 5
На тело, которое подвешено к пружине, действует вертикальная вынужденная сила
Определить динамический коэффициент, если круговая частота свободных колебаний тела
Решение. Сравнивая заданное в условиях значение для вынужденной силы с выражением (Д3.17):
получим, что частота ее изменения
Поскольку 
Коэффициент динамичности 
Ответ:
Задача 6
Дифференциальное уравнение колебательного движения материальной точки имеет вид:
Определить коэффициент динамичности
Решение. Сравнивая заданное в условиях задачи уравнение колебательного движения с (Д3.18):
получим:
Поскольку 

Ответ:
Задача 7
Материальная точка М массой 



Определить закон движения точки, если в начальный момент 
Решение: Дифференциальное уравнение движения материальной точки М в данном случае имеет вид:
или
Уравнение (1) является дифференциальным уравнением вынужденных колебаний (Д3.18), в котором: 



Поскольку 
В нашем случае это уравнение будет выглядеть:
или
Учитывая, что 
Окончательно,
Перейдем к нахождению постоянных 

Подставим в уравнение (2) и (3) начальные условия.
При
Тогда
или
Сжатые сведения по теории динамики относительного движения материальной точки
Относительным движением материальной точки называется ее движение относительно неинерциальной (подвижной) системы отсчета, которая движется относительно инерциальной (условно недвижимой) системы.
Основное уравнение динамики относительного движения материальной точки имеет вид:
где




Отметим, что силы инерции направлены в сторону, противоположную соответствующим ускорениям.
Таким образом, изменение относительного движения точки может происходить по двум причинам: во-первых, вследствие взаимодействия точки с другими материальными точками (активные силы и реакции связей), во-вторых, в следствии ускоренного движения подвижной системы отсчета относительно недвижимой системы отсчета (силы инерции).
Кориолисовая сила инерции
направлена перпендикулярно плоскости, в которой лежат векторы 

где 

Кориолисовая сила инерции равна нулю, если точка неподвижная относительно подвижной системы отсчета ( 



Переносная сила инерции
Конкретный вид переносной силы инерции 
1. Подвижные оси координат осуществляют неравномерное вращение вокруг неподвижной оси.
В этом случае
где 

Величины центробежной и вращательной сил инерции определяются по формулам:
где 


Тогда основное уравнение динамики относительного движения точки имеет вид:
2. Подвижные оси координат осуществляют равномерное вращение вокруг неподвижной оси.
В этом случае, 

Основное уравнение динамики относительного движения точки в данном случае имеет вид:
3. Подвижные оси координат движутся поступательно.
В этом случае 

Если поступательное движение прямолинейное, то
где 
По величине
Основное уравнение динамики относительного движения точки тогда будет иметь вид:
Если поступательное движение криволинейное, то
где 

Величины нормальной и касательной сил инерции определяются по формулам:
где 

Основное уравнение динамики относительного движения точкиттогда будет иметь вид:
4. Точка находится в состоянии покоя относительно подвижной системы координат.
Поскольку



Порядок решения задач динамики относительного движения материальной точки
1. Изобразить материальную точку в произвольном положении.
2. Разложить абсолютное движение материальной точки на относительный и переносной, выбрать неподвижную систему координат, связанную с телом, которое осуществляет переносное движение.
3. Записать начальные условия относительного движения материальной точки.
4. Изобразить на рисунке активные силы, которые приложены к точке.
5. Определить переносное и кориолисовое ускорение переносную и кориолисовую силы инерции, добавить их к активным силам, которые действуют на материальную точку.
6. Сохранить уравнение относительного движения в векторной форме.
7. Спроектировать векторное уравнение на оси выбранной подвижной системы координат.
8. Проинтегрировать полученные дифференциальные уравнения, определить постоянные интегрирования с помощью начальных условий.
9. Определить величины, которые ищутся.
Примеры решения задач
Задача 1
Шар М массой 



Определить переносную силу инерции шара.
Решение. Сначала определим, что относительным движением точки М будет ее движение относительно трубы, а переносным движением будет вращение вертикального вала 1, то есть, можно обозначить его угловую скорость 

где m — масса материальной точки,

Поскольку подвижная система координат которая связана с телом, осуществляет вращательное движение, то переносное ускорение состоит из нормального и тангенциального ускорений:
В этом случае
где
а 
Поскольку вал 1 вращается с постоянной угловой скоростью, то 
Таким образом, в данной задаче переносное ускорение точки состоит только из нормального ускорения:
Нормальное ускорение точки М направлено слева, в центр вращения точки (рис.1), а переносная сила инерции 
По модулю переносная сила инерции равна:
Ответ:
Задача 2
Трубка вращается вокруг оси О (рис.1) по закону 

Определить модуль кориолисовой силы инерции шара в момент времени
Решение. Кориолисова сила инерции по определению равна:
где 
Направлена 
В общем случае 
Вычислим модуль кориолисового ускорения в соответствии с условиями данной задачи
Вращение трубки вокруг оси О является переносным движением для шара М. Закон вращательного движения задан:
следовательно, закон изменения угловой скорости имеет вид:
а при
Поскольку значение угловой скорости положительное, то вращение трубки совпадает с направлением угла отсчета 
Перемещение шара вдоль трубки является относительным движением, уравнение которого задано в виде:
Тогда, скорость относительного движения шара определится с выражения:
а при
Поскольку вектор угловой скорости 



а величина кориолисовой силы инерции:
Определим направление 

Если (по правилу Жуковского) повернуть вектор относительной скорости 


Ответ:
Задача 3
Тело весом 2 Н положено на гладкую грань трехгранной призмы, вторая грань которой лежит на горизонтальной плоскости.
Определить, какое горизонтальное ускорение должна иметь призма, чтобы тело не двигалось относительно призмы, и какое давление вызывает тело на призму в этом случае, если
Решение. Если тело находится в состоянии относительного спокойствия по отношению к призме, которая движется, то геометрическая сумма приложенных к телу сил и переносной силы инерции равны нулю.
К телу приложены сила притяжения 




Тогда
Спроектируем это уравнение на оси 

С первого уравнения найдем модуль ускорения
С учетом числовых значений:
Определим переносную силу инерции:
Из второго уравнения определим модуль реакции призмы:
С учетом числовых значений:
Давление R тела на призму по модулю равно реакции N, но направлено в противоположную сторону.
Ответ:
Задания темы Д3
Груз массой m закреплен на упругом подвесе в лифте (рис. д3.12), который движется вертикально вверх по закону 



Найти закон движения груза относительно лифта 
Напоминаем, что схема подвеса (рис. Д3.12) определяется первой цифрой шифра, а номер варианта в таблице Д3.1 определяется второй цифрой шифра.
В таблице Д3.1 кроме коэффициентов 








Указания. Сначала надо изобразить расчетную схему, для чего пружины, которые прикреплены к грузу (по условию задачи их будет две), заменить одной с эквивалентной жесткостью 




Затем необходимо составить дифференциальное уравнение. относительного движения (относительно лифта) груза, который рассматривается в задаче, для чего присоединить к действующим силам переносную силу инерции. При этом следует помнить, что сила инерции направлена противоположно соответствующему ускорению. Полученное линейное неоднородное дифференциальное уравнение второго порядка следует проинтегрировать с учетом начальных условий.
Пример решения темы Д3
Дано:
Определить:
Решение. Заменяем систему из двух пружин (рис. Д3.13) одной пружиной с эквивалентной жесткостью. Поскольку пружины установлены параллельно, то жесткость эквивалентной пружины равна:
Создадим расчетную схему колебательной системы (рис.Д3.14).
При неподвижном лифте в положении статического равновесия груза эквивалентна пружина, длина которой в недеформированном состоянии 

Из условия равновесия следует, что:
Свяжем с лифтом подвижную систему отсчета 

Рассмотрим груз в положении, при котором 
Изобразим все силы, действующие на груз: 



Запишем уравнение относительного движения груза в векторной форме и в проекциях на ось
В уравнении (2):
Учитывая, что оси 

Тогда
Подставляя все эти величины в (2) и учитывая, что 
Поделив на массу 
Обозначим в уравнении (4):
окончательно получим дифференциальное уравнение относительного движения груза (уравнение затухающих колебаний)
где
Уравнение (5) линейное неоднородное дифференциальное уравнение второго порядка. Его общее решение представляет собой сумму двух решений: 

то есть
Общее решение однородного уравнения 
где 
Тогда с учетом , что 
Частичное решение уравнения (5) будем искать в виде его правой части, то есть:
Для определения Д находим 
Отсюда
Поскольку 
* В тех вариантах, где 



этих уравнений 



Для определения постоянных интегрирования 

В начальный момент времени, когда
Подставляя эти начальные данные в уравнение (9) и (10) находим 


Таким образом уравнение (9) примет окончательный вид:
Ответ: закон движения груза относительно лифта
Теоремы о движении центра масс и об изменении количества движения механической системы
Краткие сведения по теории о движении центра масс механической системы:
Механической системой или системой материальных точек называется такая совокупность материальных тел (точек), в которой положение и движение каждого
тела (точки) зависит от положения и движения всех других.
Частичным случаем механической системы является абсолютно твердое тело, которое рассматривается как система взаимодействующих материальных точек, расстояние между которыми не меняется.
Внешними силами 
Замкнутой, или изолированной системой, называется механическая система, на которую не действуют внешние силы.
Внутренними силами 
Свойства внутренних сил
1. Геометрическая сумма (главный вектор) всех внутренних сил равен нулю:
2. Сумма моментов (главный момент) всех внутренних сил системы относительно любого центра О или оси, например 
или
Массой М механической системы называется сумма масс всех тел (точек), которые входят в данную систему:
Центром масс или центром инерции механической системы называется точка С, положение которой относительно выбранной системы отсчета определяется радиус вектором 
где М — масса всей системы;


В декартовой системе координат положения центра масс определяется по формулам:
Теорема о движении центра масс механической системы
Произведение массы М системы на ускорение ее центра масс 
В проекциях на оси декартовой системы координат уравнение (Д4.5) имеет вид:
Из теоремы (Д4.5) в виде двух последствий следует закон сохранения движения центра масс системы:
1. Если главный вектор внешних сил равен нулю, то вектор скорости центра масс остается постоянным, то есть:
если
В частности, если в начальный момент времени
то центр масс не будет перемещаться. Если 
2. Если главный вектор внешних сил не равен нулю, но его проекция на любую ось равна нулю, то соответствующая проекция скорости центра масс остается
постоянной, то есть:
если 
то 
В частности, если в начальный момент 

Порядок решения задач на применение теоремы о движении центра масс
Рекомендуется следующая последовательность решения задач:
1. Изобразить на рисунке все внешние силы, которые действуют на систему.
2. Выбрать систему координат.
3. Записать теорему о движении центра масс в векторной форме.
4. Спроектировать это векторное уравнение на оси координат.
5. Вычислить суммы проекций всех внешних сил на оси координат и подставить их в проекции уравнения движения.
6. Решить полученные уравнения и найти величины, которые надо определить.
Примеры решения задач
Задача 1
Определить главный вектор внешних сил, действующих на колесо весом Р, которое скатывается без скольжения с наклонной плоскости, если его центр масс С движется по закону
Решение. Покажем внешние силы, которые действуют на колесо: силу притяжения 

Запишем теорему про движение центра масс в векторной форме:
Выберем систему координат 

Поскольку 

Найдем проекцию ускорения центра масс на ось
Итак,
Ответ: .
Задача 2
Колесо весом Р и радиусом r катится с скольжением по прямолинейной горизонтальной рейке в следствии действия устойчивой силы 
Определить скорость центра масс колеса, если в начальный момент оно
находилось в покое. Коэффициент трения скольжения равен
Решение. На колесо действуют внешние силы: 



Запишем теорему о движении центра масс колеса в векторной форме:
где 
Выберем систему координат 

При движении колеса 

Поскольку при качении колеса со скольжением сила трения достигает своего максимального значения, то
Подставим (3) в первое из уравнений (1) и получим:
Поскольку 
Согласно начальным условиям при 
Итак, закон изменения скорости центра масс колеса С имеет вид :
Ответ:
Задача 3
Однородный стержень 


массой 

Определить, какое смещение получит стержень 2, если нить в точке А оборвется и стержень 1 упадет на стержень 2 (рис. 1, б). Силами трения в направляющих 
Решение. Покажем все внешние силы, что действуют на материальную систему, состоящую из стержней 1 и 2. Внешними силами будут: 





Выберем прямоугольную систему координат 


где 

В данной задаче все внешние силы перпендикулярные к оси 


Поскольку в начальный момент времени система не двигалась, то есть
Таким образом, абсцисса центра масс механической системы не зависит от перемещения стержней, которые входят в систему, и остается неизменной по отношению к неподвижной системе координат
Запишем выражение для определения абсциссы центра масс системы в начальный момент времени:
где 

Не нарушая общности задачи, примем, что центр масс стержня 2 совпадает с центром шарнира D.
Тогда (рис 1а):
С учетом последней зависимости и того, что


При обрыве нити, удерживающей стержень 1, под действием
силы притяжения 
2 показано на рис. 1, б.
Запишем выражение для определения абсциссы 
где 

Определим новые значения абсцисс 


С учетом (4) выражение (3) приобретёт вид:
или
Откуда
Поскольку 
Решив данное уравнение относительно 
Таким образом, при падении стержня 1 на стержень 2 система сместится слева на расстояние
Ответ:
Теоремы об изменении количества движения материальной точки и механической системы
Количеством движения материальной точки называется векторная величина 

вектором скорости, то есть:
Единицей количества движения в системе СИ является килограмм метр в секунду:
Теорема об изменении количества движения материальной точки в дифференциальной форме имеет вид:
то есть производная по времени от количества движения материальной точки равна геометрической сумме всех действующих сил на эту точку.
Теорема об изменении количества движения материальной точки в интегральной форме:
то есть изменение количества движения материальной точки за некоторый промежуток времени равен геометрической сумме импульсов всех сил, действующих на эту точку.
Импульс силы 



Векторному уравнению (Д4.11) соответствует три уравнения в проекциях на оси декартовой системы координат:
Количеством движения механической системы называется векторная величина 
Количество движения системы можно также выразить через массу М всей системы и скорость 
Теорема про изменения количества движения системы в дифференциальной форме выражается формулой:
то есть производная по времени от количества движения механической системы равна главному вектору внешних сил, которые действуют на систему.
Если спроектировать векторное уравнение (Д4.16) на оси декартовой системы координат, то получим запись теоремы в скалярном виде:
Из теоремы в виде двух выводов следует закон сохранения количества движения механической системы:
1. Если главный вектор внешних сил равен нулю, то количество движения системы остается постоянным, то есть:
если
2. Если главный вектор внешних сил не равен нулю, но его проекция на любую ось равна нулю, то проекция количества движения системы на эту ось остается постоянной, то есть:
если 
то 
Наконец заметим, что поскольку в формулы, которые выражают обе теоремы, внутренние силы не входят, то изменить количество движения механической системы и движение ее центра масс могут только внешние силы.
Если обозначить количество движения системы в начальный момент времени 

то есть изменение количества движения механической системы за некоторый
промежуток времени равен геометрической сумме импульсов внешних сил 
Если спроектировать векторное уравнение (Д4.20) на оси декартовой системы координат, то получим запись теоремы об изменении количества движения механической системы в интегральной форме в скалярном виде:
Порядок решения задач на применение теоремы об изменении количества движения точки и механической системы
Для материальной точки:
1. Изобразить на рисунке все силы, которые приложены к материальной точки, то есть активные силы и реакции связей.
2. Выбрать систему координат.
3. Записать теорему об изменении количества движения точки в векторной форме.
4. Спроектировать векторное уравнение на оси выбранной системы координат.
5. Решить полученные уравнения и определить искомые
величины.
Для механической системы:
1. Изобразить на рисунке все внешние силы.
2. Выбрать систему координат.
3. Записать теорему об изменении количества движения системы в векторной форме.
4. Спроектировать векторное уравнение на оси выбранной системы координат.
5. Решить полученные уравнения и определить искомые величины
Примеры решения задач
Задача 1
Железнодорожный поезд движется по горизонтальной и прямолинейной области пути (рис.1). При торможении до полной остановки развивается сила сопротивления, равная

Определить время t и путь L торможения.
Решение. Изобразим силы (рис.1), которые действуют на поезд во время торможения: силу тяжести поезда 


Выберем систему координат. Поскольку движение прямолинейное и горизонтальное, достаточно рассмотреть движение в направлении оси
Будем рассматривать поезд как материальную точку. Запишем теорему об изменении количества движения поезда в интегральной форме (Д4.11):
где m — масса поезда;



Спроектируем векторное уравнение (1) на ось 
Проекции импульсов сил 




Сила сопротивления 
Скорость в конце области торможения равна нулю, то есть
Окончательно, уравнение импульсов (2) в проекции на ось 

Откуда



Запишем основной закон динамики для материальной точки в проекции на ось
Поскольку 

В этом случае ускорение поезда определяется из формулы:
то есть
Тогда
Ответ:
Задача 2
По шероховатой наклонной плоскости, которая образует с горизонтом угол 
Определить время T, за которое тело пройдет путь длиной 

Решение. Во время движения на тело действуют сила трения тела 


Запишем теорему об изменении количества движения в векторной форме:
Направим ось 
Проекция импульса нормальной реакции 


Учитывая, что во время движения сила тяжести 

Кроме того:
С учетом записанного уравнения (2) имеет вид:
Найдем силу трения:
Подставив 
или
Тогда
Поскольку 

Воспользовавшись полученной зависимостью, сначала определим ускорение тела, а после этого — время движения. Поскольку для равноускоренного движения 


По формуле 


Из этой формулы находим время движения T:
Ответ:
Задача 3
По понтонному мосту массой М движется автомобиль массой m по закону
Пренебрегая сопротивлением воды определить:
1. Скорость 
2. Силу 
Решение.
1. Сначала рассмотрим случай, когда мост не прикреплен к берегу, то есть 

На систему, которая состоит из моста и автомобиля, действуют внешние силы: сила тяжести моста 


Все силы, которые действуют на систему, являются вертикальными.
Свяжем с берегом неподвижную систему координат 

Закон движения автомобиля 
Таким образом, относительная скорость автомобиля от 
а абсолютная скорость автомобиля 
где 
Поскольку скорость автомобиля зависит от времени, то для решения задачи воспользуемся теоремой о изменении количества движения системы в дифференциальной форме в проекции на ось 
Учитывая, что
где 
Проекция количества движения системы на ось 

где
Тогда
или
Подставим (2) в (1) и сдиференцируем по времени:
Таким образом, чтобы найти выражение для 

Окончательно получим
Знак минус указывает на то, что скорость моста направлена в сторону, которая противоположна движению автомобиля.
2. Рассмотрим случай, когда мост прикреплен тросами к берегу.
В этом случае к вертикальным силам 


Используем дифференциальное уравнение изменения количества движения в проекции на ось 
Задания темы Д4
Механическая система состоит из грузов 1 массой
и прямоугольной вертикальной плиты 3 массой 
когда скорость плиты 





Определить зависимость 
Указание. Задачу темы Д4 решить двумя способами:
а) применяя теорему о движении центра масс механической системы;
б) применяя теорему об изменении количества движения механической системы.
Как и в предыдущих задачах первая цифра шифра определяет номер рисунка на рис. Д4.2, а вторая — вариант в Д4 таблицы.
Пример решения темы Д4
Дано:
Определить:
Решение. Рассмотрим механическую систему, которая состоит из плиты 3 и грузов 1 и 2 в произвольном положении (рис. Д4.3).
Покажем все внешние силы, которые действуют на систему: силы притяжения

Проведем координатные оси 

точку, 

а) Определим 
Поскольку 

где 
Поскольку все внешние силы, которые действуют на систему, вертикальные, то 



Отделяя переменные и интегрируя последнее уравнение получим:
где 

Из формулы (Д4.4) определим значение:
Выразим координаты 


а абсцисса второго груза:
Подставляя (4) и (5) в (3), получим:
После подстановки зависимостей для 
Подставляя уравнение (6) в (2), получим:
отсюда уравнения движения плиты будет иметь вид:
Для определения скорости плиты 
Постоянное интегрирование 


Таким образом скорость плиты 3 будет меняться по закону:
где
Подставляя полученные выражения для 

В соответствии с (10) выражения (11) и (13) равны, то есть:
Отсюда окончательно получим:
Ответ: скорость движения плиты 3, как функция времени
Замечания. Поскольку две теоремы являются разными формами одного и того же закона, то выбор, какую из них использовать, зависит от характера задачи, которая решается. При изучении движения одного твердого тела (или системы тел) можно с одинаковым успехом пользоваться любой из этих форм. Если же рассматривается движение
сплошной среды (жидкости или газа), то понятия про центр масс системы практически теряет свое содержание. В этих случаях используют теорему об изменении количества
движения.
Теорема о смене кинетической энергии механической системы
Краткие сведения по теории
Кинетической энергией материальной точки называется скалярная положительная величина, равная половине произведения массы точки на квадрат ее скорости:
Единицей кинетической энергии в системе CИ является Джоуль (Дж):
Кинетическая энергия механической системы n материальных точек (тел) называется арифметическая сумма кинетических энергий всех точек (тел) системы:
Кинетическая энергия твердого тела в простейших случаях его движения исчисляют по формулам:
а) при поступательном движении тела
где M — масса тела;
V — скорость любой его точки.
б) при вращении тела вокруг неподвижной оси
где 

в) при плоскопаралельном движении тела
где M — масса тела;



Элементарной работой 
называется скалярная мера действия силы, равная скалярной добыче силы на элементарное перемещение 
где 

В зависимости от угла 





Кроме того, работа равна нулю, если в данный момент 

Единицей работы в СИ является Джоуль (Дж):
Выражение элементарной работы переменной силы через проекции силы и элементарного перемещения на оси декартовых координат имеет вид:
Работа А переменной силы 


где 
к траектории в данной точке, или в координатном виде:
В некоторых отдельных случаях работа вычисляется по готовым формулам:
1. Работа постоянной силы на прямолинейном перемещении ее точки приложения
где S — путь, который прошла точка приложения силы


2. Работа силы тяжести
где 

Знак «+» берется, если точка приложения движется вниз, знак «-«, если вверх.
3. Работа силы упругости
где 


Работа будет положительной, если, 

4. Работа силы, которая приложена к телу, которое вращается вокруг неподвижной оси
где 



Если 
Теорема об изменении кинетической энергии материальной точки в интегральной форме
Изменение кинетической энергии материальной точки на ее перемещении
равняется сумме работ всех сил, которые действуют на эту точку, в пределах того же перемещения:
Если сумма работ сил положительная, то 

В случае несвободного движения точки в правую часть уравнения (Д5.15) кроме работ активных сил войдут также и работы реакций связей.
Если материальная точка движется по гладкой поверхности (сила трения равна нулю), то реакция поверхности будет направлена перпендикулярно к поверхности (перпендикулярно к перемещению точки) и ее работа будет равняться нолю. Таким образом, при перемещении материальной точки по гладкой поверхности изменение кинетической энергии будет определяться суммой работ на этом перемещении только приложенных к точке активных сил.
Теорема об изменении кинетической энергии механической системы в интегральной форме
Изменение конечной энергии системы на ее конечном перемещении (0-1) равно сумме работ всех внешних и внутренних сил системы на этом перемещении:
Для неизменной системы (твердое тело, гибкая нерастяжимая нить) 
Изменение кинетической энергии неизменной системы на ее конечном перемещении (0-1) равняется сумме работ всех внешних сил, действующих на систему на этом перемещении.
Порядок решения задач на применение теоремы об изменении кинетической энергии в интегральной форме
Решение задач с помощью теоремы об изменении кинетической энергии в интегральной форме рекомендуется проводить в следующей последовательности:
1. Показать на рисунке все внешние силы системы.
2. Вычислить сумму работ всех внешних сил на перемещении точек системы.
3. Вычислить кинетическую энергию механической системы в начальном и конечном ее состояниях.
4. Пользуясь результатами подсчетов по пунктам 2 и 3, записать теорему об изменении кинетической энергии механической системы и определить величину параметры, которой нужно найти.
Примеры решения задач
Задача 1
Определить наименьшую работу А, которую необходимо выполнить, чтобы поднять на высоту 


Решение: Изобразим груз в произвольном положении на наклонной плоскости и покажем все силы, что на его действуют (рис.1): силу притяжения 

Работа, которая тратится на поднимание груза на высоту h = 5 м, равна сумме робот силы трения вдоль длины АВ и силы притяжения на перемещении ВС точки ее приложения.
Нормальная реакция работы не выполняет, поскольку она перпендикулярна перемещению.
Вычислим работу силы трения:
Поскольку 
Работа силы притяжения в нашем случае отрицательна, поскольку груз движется вверх, и равен:
Полная работа, потраченная на поднимание груза, равняется:
Ответ:
Задача 2
Тело А (рис.1) удерживается в равновесии на гладенькой наклонной поверхности, расположенной под углом 
L .
Определить сумму работ А всех сил, приложенных к телу на этом перемещении, если сила притяжения тела 

Решение. К телу приложены следующие силы: сила притяжения 


Ось 
Поскольку 
или
Окончательно,
Работа нормальной реакции R равна нулю, поскольку эта сила перпендикулярна к перемещению тела, то есть
Итак,
Ответ:
Задача 3
Материальная точка М массой m движется прямолинейно по горизонтальной плоскости по закону 

Определить работу этой силы при перемещении точки ее приложения из первоначального положения 
Решение. Сила, действующая на материальную точку М, меняется с изменением времени. Итак, для определения работы этой силы необходимо воспользоваться уравнением (Д5.8):
где 
В нашем случае заданная сила 

Таким образом, уравнение (1) имеет вид:
Найдем зависимость между силой F и перемещением S, исключив параметр t, входящий в выражения для значение силы и перемещения:
Подставив новое выражение для силы F в уравнение (2), получим:
Вычислим этот определенный интеграл:
Ответ:
Задача 4
На рис. 1 изображен поднимающий механизм лебедки. Груз А весом
поднимается с помощью невесомого и нерастяжимого троса, который переброшен через блок С и намотан на барабан В радиусом r и весом 

где 
Определить скорость груза А в момент, когда он поднимется на высоту h. Массу барабана В считать равномерно распределенной вдоль его обода. Блок С — сплошной
диск весом 
Решение. Изобразим на рисунке все внешние силы, которые действуют на барабан В, блок С и груз А: силы притяжения 



Запишем теорему об изменении кинетической энергии системы (Д5.16):




Поскольку в начальный момент времени система находилась в состоянии покоя, то
В связи с тем, что трос не растягивается и при движении системы находится в натянутом состоянии, сумма работ внутренних сил системы равна нулю, следовательно
При поднятии груза А на высоту h сумма работ равна:
Поскольку точки приложения сил 

Работа силы 
Поскольку вращающийся момент является переменным, то его работа определится путем интегрирования (Д5.13):
Определим угол 
Итак,
Таким образом
Перейдем к подсчету кинетической энергии системы в конечном положении:
где 


Груз А движется поступательно и его кинетическая энергия равна (Д5.3):
Диск С осуществляет вращательное движение, его кинетическая энергия определяется из выражения (Д5.4):
где 

Поскольку диск C сплошной, 
где 
Поскольку линейная скорость обода диска равна скорости груза, угловая скорость вращения 
Итак,
Кинетическая энергия барабана В, поскольку он осуществляет вращательное движение, которое равно:
Поскольку масса барабана В распределена по ободу, то:
Угловую скорость барабана вычтем из условия равенства линейных скоростей на ободах диска и барабана:
Отсюда
Таким образом
Кинетическая энергия системы в конечном положении равна:
Итак, теорема про изменение кинетической энергии системы (1) имеет вид:
Решая это уравнение относительно 

Ответ:
Задания темы Д5
Механическая система, схема которой показана на рис. Д5.1, а исходные данные приведены в таблице Д5, состоит: с четырех тел массами:
груза 1; двоих ступенчатых шкивов 2 и 3, радиусы степеней которых 




Под действием силы 






Определить значения скорости, которая приведена в таблице, в тот момент времени, когда тело 1 переместится на расстояние
Указания. Задача Д5- на использование теоремы о изменении кинетической энергии механической системы. Учтите, что все скорости, которые входят в выражения для кинетической энергии системы, необходимо выразить через ту скорость
(линейную или угловую), которую в задаче надо определить.
При вычислении кинетической энергии тела, которое движется плоскопараллельно, для установления зависимости между скоростями разных точек тела или между их угловой
скоростью и скоростью центра масс надо воспользоваться мгновенным центром скоростей. Кроме того, при вычислении работ внешних сил и моментов сил надо все перемещения выразить через заданное перемещение 
Пример решения темы Д5
Определить: скорость 
Решение. Рассмотрим движение неизменно механической системы (рис.Д5.2)
Изобразим внешние силы и моменты сил сопротивления движению, которые действуют на тело системы: 






Для определения 
где 



Поскольку в начальном положении система находится в состоянии покоя, то 

Величина T равняется сумме кинетических энергий всех тел системы:
Запишем выражения для 
Все скорости, которые входят в уравнение (4) 



Тогда
Угловая скорость ступенчатого шкива 3 равняется:
Поскольку
Тогда
Угловая скорость 
Поскольку
Скорость точки В равняется:
Тогда
Скорость 
В целом
и окончательно:
Найдем сумму работ внешних сил, которые приложены к телам системы на заданном перемещении:
Учитывая, что


Работа переменной силы 
Работа силы тяжести
Робота силы трения
Робота момента силы трения подшипника шкива 2:
Робота момента силы трения подшипника шкива 3:
Работа силы тяжести
Работа момента пары сил сопротивления качению катка 4:
Величины 


Из (11) следует 
Из (10) следует 
Из (9) следует 
Из (8) следует 
Таким образом:
Подставляя 

Согласно с (2) приравниваем (12) и (30):
Откуда
Ответ: скорость движения центра масс катка
Принцип даламбера
Краткие сведения из теории:
Принцип Даламбера является одним из методов решения задач динамики, использование которого позволяет составлять уравнение движения материальной точки и механической системы в форме уравнений статики, которые проще чем уравнение динамики.
Принцип Даламбера для материальной точки
Рассмотрим материальную точку М, которая движется и на которую действуют заданная сила 






Добавим к силам 


а по модулю:
Сила, которая по модулю равна произведению массы точки на модуль ее ускорения и направлена противоположно ускорению, называется силой инерции.
Совокупность сил 

Итак, при движении материальной точки в каждый данный момент времени совокупность заданной силы


В этом состоит принцип Даламбера для материальной точки, значение которого заключается в том, что при его применении к задачам динамики уравнения движения составляются в форме хорошо известных уравнений равновесия.
При проектировании векторного равенства (Д6.1) на декартовые оси координат, получаем выражения для проекций силы инерции на эти оси:
Проецируя то же векторное равенство на природные оси, получим проекции силы инерции на касательную, нормаль и бинормаль к траектории:
Составляющие силы инерции 

Принцип Даламбера для механической системы
Если к каждой точки механической системы. которая движется, условно приложить соответствующую силу инерции, то в любой момент времени активные силы, которые действуют на эту точку, реакции связей и сила инерции образуют уравновешенную систему сил, то есть
где 


Из статики известно, что геометрическая сумма сил, которые находятся в равновесии, и сумма их моментов относительно любого центра О равняется нулю, поэтому
где 





В проекциях на оси декартовой системы координат уравнение (6.6) и (6.7) дают или шесть уравнений для произвольной пространственной системы сил:
или три уравнения для произвольной плоской системы сил (основная форма):
Приведение сил инерции точек твердого тела к простому виду
Как известно, систему сил можно привести к силе, которая равна главному вектору и до пары сил с моментом, который равен главному моменту всех сил системы.
Приведение сил инерции точек твердого тела дает следующие результаты.
1. При поступательном движении тела силы инерции приводятся к равнодействующей, которая приложена в центре масс С тела. Равнодействующая 
этому ускорению:
2. При вращении тела вокруг проходящей оси через центр масс тела, силы инерции приводятся к одной паре, которая лежит в плоскости, перпендикулярной к оси
вращения тела и имеет момент (рис Д6.2):
где 

Направление пары сил является противоположным направлению углового ускорения
3. При плоском движении силы инерции приводятся к результирующей силы, которая равна 



Порядок решения задач на применение принципа Даламбера
Решение задач с помощью принципа Даламбера (метода кинетостатики) рекомендуется выполнять в следующей последовательности:
1. Изобразить на рисунке активные силы, которые приложены к каждой материальной точке;
2. Изобразить реакции связей;
3. Добавить к активным силам и реакциям связей силы инерции материальных точек системы;
4. Выбрать систему координат;
5. Составить уравнение равновесия всех сил;
6. Решив составную систему уравнений, определить величины, которые ищутся.
Примеры решения задач
Задача 1
Груз М весом 1 Н, который подвешен на нитке длиной 30 см в неподвижной точке О, представляет собой конический маятник, то есть описывает круг в горизонтальной плоскости, при этом нитка составляет с вертикалью угол 
Определить скорость груза V и натяжение нити Т.
Решение. На груз М действуют сила притяжения 


Подсчитаем силу инерции груза. Сила инерции 
сторону, противоположную 
Свяжем с точкой М естественную систему координат 



Согласно принципу Даламбера геометрическая сумма сил 

Спроектируем это векторное уравнение на оси выбранной системы координат:
на ось
на ось
на ось
Со второго уравнения определим натяжение нити
Из первого уравнения находим скорость 
Ответ:
Задача 2
Определить опорные реакции подпятника А и подшипника В поворотного крана (рис. 1) при поднимании груза Е весом 30 кН с ускорением 
Решение. На кран действуют силы притяжения крана 


Для уравновешенной системы сил добавим силу инерции поднимающегося груза Е
с ускорением
Сила инерции 
Перейдем, согласно методу кинетостатики, к составлению уравнений равновесия крана при наличии активных сил, реакций связей и силы инерции. Уравнение равновесия выглядит так:
Решая эти уравнения, находим неизвестные величины:
Ответ:
Задача 3
Барабан А (рис. 1), весом Р и радиусом r, вращается вокруг горизонтальной оси O в результате опускания тела B, весом Q, которое подвешено к нерастяжимому и невесомому канату, который намотанный на барабан.
Определить угловое ускорение 
Решение. На систему действуют внешние (активные) силы: силы тяжести барабана 


Данная система сил не является уравновешенной.
Согласно принципу Даламбера, если к активным силам и реакциям связей, которые действуют на систему, добавить силы инерции, то полученная система сил будет уравновешенной и к ней можно применить уравнение равновесия.
Найдем силы инерции, которые надо добавить к телам данной системы.
Тело В движется вниз с некоторым ускорением 
Сила инерции 

Поскольку барабан вращается вокруг оси, которая проходит через его центр масс, то силы инерции барабана сводятся к паре сил с моментом 
равняется:
где 
Учитывая, что барабан представляет собой сплошной диск, то:
Тогда
Направление момента 
Поскольку систему сил после приложения сил инерции можно рассматривать как такую, которая находится в равновесии, то запишем равенство нуля моментов сил относительно оси вращения:
или
Сократив на 
Откуда
Для определения натяжения каната воспользуемся высвобождаемым принципом: разрежем квадрат и покажем активные силы , которые действуют на тело В (рис.2): силу притяжения 
Согласно с принципом Даламбера добавим к этим силам силу инерции 
Запишем уравнение равновесия всех сил, включая и силу инерции, на вертикаль:

Откуда
Подставим в полученное уравнение выражение для
Тогда
Ответ:
Задание темы Д6
Вертикальный вал, который закреплен в подпятнике в точке А и в цилиндрическом подшипнике в точке В (рис. Д6.4), вращается с постоянной угловой скоростью






Пренебрегая весом вала, определить реакции подпятника и подшипника, а также вычислить во сколько раз радиальные динамические составляющие реакций отличаются
от статических. При расчетах принять ускорение свободного падения
Указания. Задача Д6 -на использование принципа Даламбера к изучению движения материальной системы. Следует помнить, что силы инерции направлены противоположно соответствующим ускорениям, и поскольку по условию задачи 





Пример решения темы Д6
Определить:
Решение. Согласно данным изображаем вал, который закреплен подпятником в точке A и подшипником в точке B (рис.Д6.2).
К валу жестко прикреплены: в точке K перпендикулярно оси вращения маховик, центр масс 


Выберем систему координат Kxyz, которая будет вращаться вместе с валом, так, чтобы стержень лежал в плоскости 


Покажем активные силы, которые действуют на систему: силы притяжения диска
и стержня 



Силы притяжения равны по величине:
Согласно принципу Даламбера, присоединим к этим силам центробежные силы инерции элементов диска и стержня.
Для каждого элемента диска массой 


условию задачи равняется нулю
Эти силы, которые совпадают в точке K, могут быть заменены равнодействующей, 
Поскольку угловое ускорение диска равно нулю, то главный момент сил инерции элементов диска тоже равняется нулю.
Таким образом, система сил инерции элементов диска сводится к одной равнодействующей 

Поскольку вектор силы можно переносить вдоль его линии действия, то будем считать, что сила 
Для каждого элемента стержня массой 



где 
Поскольку все элементарные силы 



Модуль этой равнодействующей равен главному вектору сил инерции стержня:
Поскольку силы 




Согласно принципу Даламбера внешние силы и силы инерции, которые приложены к системе, образуют уравновешенную систему сил. Составим для этой плоской системы
три уравнения равновесия:
В уравнении (7) плечи

Выразив из уравнений (5) (7) неизвестные реакции и подставив в полученные уравнения соответствующие величины из (1), (2), (4) найдем составляющие реакций связей:
из (7) следует
Из (6) следует
Из (5) следует
Тогда полные реакции:
Чтобы определить статические реакции подшипника и подпятника следует в уравнениях равновесия (5) 
Тогда уравнения (5) 
Из (10) следует
Из (9) следует
Из (9) следует
Впрочем, вычислим во сколько раз радиальные динамические составляющие реакции подшипников больше, чем статические
Таким образом, радиальные динамические нагрузки на подшипники, которые возникают благодаря силам инерции, могут быть значительно больше, чем статические нагрузки,
что необходимо учитывать при конструировании машин и механизмов.
Ответ: реакция подпятника
реакция подшипника
Дополнительные лекции и примеры по теме «Динамика»
Законы динамики, уравнения движения материальной точки. принцип даламбера
Динамикой называется раздел механики, в котором изучается движение материальных тел под действием приложенных к ним сил. В основе динамики лежат законы, сформулированные Ньютоном.
Первый закон — закон инерции, установленный Галилеем, гласит:
материальная точка сохраняет состояние покоя или равномерного прямолинейного движения» пока воздействие других тел не изменит это состояние.
Второй закон — основной закон динамики — устанавливает связь между ускорением 



Запишем этот закон в форме, которую придал ему Эйлер:
В классической механике масса т принята за постоянную величину. Масса является мерой инертности материальных тел в их поступательном движении. Запишем основной закон динамики в скалярном виде, проецируя векторные величины, входящие в равенство* на оси координат:
Третий закон формулируется следующим образом: всякому действию соответствует равное и противоположно направленное противодействие.
Этот закон устанавливает, что при взаимодействии двух тел, в каком бы кинематическом состоянии они не находились, силы, приложенные к каждому из них, равны по модулю и направлены по одной прямой в противоположные стороны.
Четвертый закон не был сформулирован Ньютоном как отдельный закон механики, но таковым можно считать сделанное им обобщение правила параллелограмма сил:
- несколько одновременно действующих сил сообщают точке такое ускорение, какое сообщала бы одна сила, равная их геометрической сумме.
Основной закон динамики можно записать в скалярном виде, спроецировав векторы либо на декартовы, либо на естественные оси координат. В первом случае получим уравнения движения материальной точки в прямоугольной декартовой системе координат:
где
Во втором случае получим естественные уравнения движения:
где
Проекция ускорения на бинормаль всегда равна нулю 
Пример решения задачи 1.14
Уравнения движения материальной точки 

Определить равнодействующую приложенных к материальной точке сил и траекторию ее движения.
Решение.
1. Определяем проекции ускорения на оси координат. Для этого сначала определим проекции скорости на те же оси:
2. Определяем проекции равнодействующей силы. Поскольку 

3. Определяем модуль равнодействующей:
4. Определяем направление равнодействующей:
Очевидно, что угол наклона равнодействующей силы по отношению к осям координат меняется.
5. Определяем траекторию движения материальной точки. Для исключения переменной 
Из полученного решения можно сделать следующий вывод: материальная точка движется по окружности радиусом г под воздействием приложенной к ней силы, которая все время направлена к центру этой окружности.
Принцип ДАламбера
Принципом Д’Аламбера называют общий метод, с помощью которого уравнениям динамики придается вид уравнений статики. Для этого вводится понятие «сила инерции материальной точки» — сила, равная произведению массы точки на ее ускорение и направленная противоположно ускорению:
Положим, что материальная точка 


Перенесем член 
Так как 
Полученное соотношение выражает принцип Д’Аламбера и формулируется следующим образом;
- геометрическая сумма всех приложенных к точке сил и силы инерции этой точки равна нулю.
Принцип Д’Аламбера применим как для свободной, так и для несвободной материальной точки, так как, освобождая материальную точку от связей и заменяя их действие пассивными силами, мы рассматриваем движение точки под действием активных и пассивных сил, которые сообщают ей ускорение.
Следует помнить, что к материальной точке инерционная сила приложена лишь условно. Фактически сила инерции приложена не к материальной точке, а к телу, сообщающему ей ускорение.
Этот метод получил широкое применение при расчетах на прочность при динамических нагрузках (см. пример 2.18 в главе 2).
Силу инерции можно разложить на касательную 

где 
В случае круговой траектории точки (радиус окружности 


Силы, действующие на точки механической системы
еханической системой называют мысленно выделенную совокупность материальных точек, взаимодействующих между собой. Механическую систему иногда называют материальной системой или системой материальных точек. Существуют системы свободных (например, Солнечная система) и несвободных материальных точек (их движения ограничены связями). Примером системы несвободных точек может служить любой механизм или машина, Все силы, действующие на систему несвободных точек, подразделяют на задаваемые (активные) силы и реакции связей (пассивные силы).
По другому признаку силы, действующие на точки любой механической системы, делят на внешние и внутренние. Условимся обозначать внешние силы 
Внешними называют силы, действующие на точки системы со стороны материальных точек, не входящих в состав данной системы.
Внутренними силами называются силы взаимодействия между материальными точками данной механической системы. Примером внутренних сил могут служить силы упругости, действующие между частицами упругого тела, принятого за механическую систему.
Одна и та же сила может быть как внешней, так и внутренней в зависимости от того, какая механическая система рассматривается. Например, реакции подшипников вала являются внешними силами по отношению к валу. Эти же реакции можно отнести к внутренним силам, если рассматривать всю установку вместе с машиной.
Таким образом, любая сила может быть внешней или внутренней, в то же время она может быть задаваемой или реакцией связи. Движение точек системы зависит как от внешних, так и от внутренних сил.
По закону равенства действия и противодействия каждой внутренней силе соответствует другая внутренняя сила, равная ей по модулю и противоположная по направлению. На основании этого можно сделать следующие выводы.
1. Главный вектор всех внутренних сил системы равен нулю:
Следовательно, и суммы их проекций на координатные оси также равны нулю:
2. Главный вектор-момент всех внутренних сил системы относительно любого центра и координатных осей равен нулю:
или
Эти уравнения имеют вид уравнений равновесия сил, произвольно приложенных в пространстве, однако в них входят внутренние силы, которые не уравновешиваются, так как они приложены к разным точкам системы и могут вызвать перемещение этих точек относительно друг друга.
Теорема о движении центра масс механической системы
Представим, что механическая система массой 


или
Дважды продифференцировав эти равенства, получим
Правые части полученных уравнений в соответствии с основным законом^намики представляют собой сумму внешних 

Учитывая, что главный вектор внутренних сил равен нулю 
Эти уравнения выражают теорему о движении центра масс системы, которая формулируется следующим образом.
Центр масс механической системы движется как материальная точка с массой, равной массе системы, к которой приложены все внешние силы, действующие на эту систему.
Отсюда следует, что внутренние силы не оказывают влияния на движение центра масс механической системы.
Пример решения задачи 1.15.
Определить перемещение плавучего крана, поднимающего груз массой 



Решение.
1. Выбираем систему отсчета (рис. 1.53, а).
2. Проставляем все внешние силы, действующие на материальные Теда данной механической системы. На плавучий кран действуют сила тяжести 

3. Запишем уравнения движения центра масс механической системы
или
4. Будем исследовать первое уравнение, так как нас интересует движение центра масс по горизонтали. Поскольку 

В начальный момент система находилась в покое, следовательно, 

Таким образом, анализ уравнения движения центра масс вдоль оси 
5. Запишем формулы для определения начального и конечного положений центра масс механической системы:
6. Выразим начальные и конечные координаты материальных тел системы в соответствии с выбранной системой отсчета (см. рис. 1.53, а и б):
7. Определяем перемещение 

или
Ответ:
Краткие исторические сведения о динамике
Законы движения тел всегда интересовали человека. Познание их было медленным и не всегда удачным. Например, Аристотель (384-322 pp. До н. С.) считал, что с прекращением действия силы, тела перестают двигаться. Только в результате длительных наблюдений над движениями, происходящими в природе, были правильно сформулированы законы движения.
Разработка основ динамики относится к 
Важную роль в развитии динамики сыграло открытие Н. Коперником (1473-1543) гелиоцентрической системы, согласно которой Земля и другие планеты вращаются вокруг Солнца. До Коперника общепринятой считалась геоцентрическая система мира К. Птолемея (
В исследованиях по небесной механике И. Кеплер (1571-1630) обобщил учение Коперника. Он установил, что орбиты планет являются не кругами, а эллипсами с незначительным эксцентриситетом. Пользуясь наблюдениям Тихо Браге (1546- 1601) над движением планет, Кеплер открыл законы их движения. Подготовительный период в развитии динамики связан с именами Леонардо да Винчи (1452- 1519), Г. Галилея (1564 1642), Р. Декарта (1596- 1650) и X. Гюйгенса (1629 1695).
Леонардо да Винчи принадлежит ряд исследований движения тела по наклонной плоскости, теории механизмов, движения воды в трубах и тому подобное. Он впервые сформулировал закон инерции. Интересно, что более поздние исследования Г. Галилея по закону инерции являются менее прогрессивными по сравнению с аналогичными исследованиями Леонардо да Винчи, поскольку Галилей ошибался, когда под движением по инерции понимал равномерное движение по кругу, а не по прямой линии.
Г. Галилей экспериментально доказал закон падения тел в пустоте, исследовав движение снаряда без учета сил сопротивления, установил закон пропорциональности между весом тела и его массой, впервые сформулировал принцип относительности классической динамики, а также исследовал движение математического маятника.
Р. Декарт проводил систематические опыты над движением тел, сталкивающихся и ввел понятие о количестве движения, как о мере механического движения, открыв закон сохранения количества движения, Декарт неправильно рассматривал его как универсальный закон природы: он считал количество движения величиной скалярной. Однако, несмотря на эту ошибку, идея Декарта оказалась плодотворной и сыграла в развитии динамики большую роль.
X. Гюйгенс решил ряд задач о движении простого и сложного физических маятников, об определении центра колебаний физического маятника. Он впервые использовал в динамике выражения для осевых моментов инерции материальной системы, а также кинетической энергии, но не называл их этими терминами. В дальнейшем Г. Лейбниц (1646-1716) развил вопрос о мерах механического движения. Между сторонниками Декарта и Лейбница возникла дискуссия о настоящей мере механического движения, которая закончилась в конце XIX в. Правильно с диалектико-материалистических позиций осветил историю этой дискуссии и раскрыл методологическую сущность вопроса о мерах механического движения Ф. Энгельс в своем труде «Диалектика природы».
Основателем динамики как целостной науки является И. Ньютон (1643 1727). Он систематизировал и обобщил исследования, связанные с динамикой, и показал пути дальнейшего развития. Он впервые сформулировал основные законы динамики, известные в современной литературе как первый, второй и третий законы Ньютона, ввел понятие массы и обобщил понятие силы. Ему принадлежит открытие общего закона природы — закона всемирного тяготения, который лежит в основе современной механики и физики. Пользуясь этим законом, он решил ряд задач теоретической и небесной механики. Главное произведение Ньютона, в котором подано четкое и систематическое изложение классической механики, называется «Математические начала натуральной философии «.Это произведение написано на латинском языке и впервые издано в 1687 г. На русский язык ее перевел А. Н. Крылов, сделал многочисленные примечания (см .: Крылов А. Н. Собрание трудов, изд-во АН СССР, 1936). Будучи одним из основателей математического анализа, Ньютон вместе с тем изложил механику синтетически. Впервые аналитически динамику изложил Л. Эйлер (1707-1783) — академик Петербургской Академии наук. Он впервые доказал одну из основных теорем динамики — теорему об изменении кинетического момента; построил теорию моментов инерции; ввел понятие потенциального силового поля и открыл один из общих принципов механики, названный его именем. Заслуги Эйлера в небесной механике, применении механики в технике (кораблестроении, турбостроении и т.д.), механике сплошных сред, теории устойчивости чрезвычайно велики. Современник Эйлера Н. В. Ломоносов (1711-1765) как энциклопедист не мог не заинтересоваться механикой, как основой естествознания в целом. Ему принадлежит открытие общего закона природы — закона сохранения материи и движения. Все законы сохранения механики и физики (закон сохранения количества движения, закон сохранения и преобразования энергии и др.) является конкретными частными случаями закона Ломоносова. Утверждая несотворимость и неуничтожимость материи и движения, способность движущейся материи в различных преобразованиям, рассматривая материю в органической связи с движением, общий закон Ломоносова и все его конкретные модификации в различных отраслях физики и естествознания являются доказательством единства мира и всеобщности движения, являясь, таким образом, естественнонаучной основой материализма.
Исследования Л. Эйлера по динамике твердого тела получили дальнейшее развитие в трудах Ж. Лагранжа, Л. Пуансот (1777-1859) и С. В. Ковалевской (1850-1891). Результаты исследований С. В. Ковалевской стали импульсом к появлению в области динамики твердого тела и ее технических приложений целого ряда научных исследований отечественных и зарубежных ученых, среди которых А.Н. Ляпунов (1857- 1918), Н Б. Делоне (1856-193I) М. Е. Жуковский (1847-1921), С. А. Чаплыгин (1869-1942). Сегодня исследования по динамике твердого тела развивают П. В. Харламов, В. Г. Демин и ряд других исследований по динамике твердого тела связан с развитием теории гироскопов и инерциальной навигации. К этому направлению относятся исследования Шулера, О.М. Крылова (1863-1945), Б. В. Булгакова (1901-1952), В. А, Павлова, Г. Магнуса, Д С. Пельпора, А. Ю. Ишлинского , Д. М. Климова, В. М. Смеляков, А. П. Бойчука, Ю. А. Карпачева и др. В конце XIX в. зародилась механика тел переменной массы, основателем которой является И. В. Мещерский (1859 1935). Этот раздел механики стал основой теории реактивного движения и межпланетных полетов, которую создал К. Э. Циолковский (1857-1935). Он получил дальнейшее развитие и практического воплощения в трудах создателя ракетной и космической техники С.П. Королева (1907-1966). В конце XX в. Украина стала мировым лидером в ракетостроении, которое возглавил С. И. Конюхов (Днепропетровск). В XX в. было установлено, что при скоростях, близких к скорости света (300 000 км / с), формулы классической механики приводят к существенных погрешностей. В этом случае нужно применять механику больших скоростей — релятивистскую механику.
Во второй половине XX в. появилось новое направление науки — робототехника, основой которого стала теоретическая механика. Особенностью робототехники является то, что она синтезирует и объединяет такие науки, как механика, кибернетика и компьютерные технологии. Большой вклад в развитие этого направления внесли: К. В. Фролов, Е. И. Воробьев, А. Г. Овакимов, Ф. Л. Черноусько, Р. Уикер, М. Вулкобратович, В. Б Ларин, В. И. Костюк, М. 3. Згуровскин и др. XX века можно назвать еще и веком механики нелинейных колебаний. Особый вклад в развитие теории нелинейных колебаний принадлежит украинским ученым Н. Н. Боголюбову, Ю. А. Митропольському, В. А. Кононенко и др.
Динамика и ее основные задачи
Динамикой называется раздел теоретической механики, в котором изучается механическое движение материальной точки, системы материальных точек и абсолютно твердого тела с учетом сил, действующих на эти подвижные объекты. В динамике синтезируются и обобщаются положения, рассмотренные в статике и кинематике, а также устанавливаются наиболее общие законы механического движения. При этом учитывается взаимодействие между телами, мерой которых является сила. Статическое измерение силы основывается на уравновешивании ее другой силой. С помощью динамометра сила, действующая на тело, определяется уравновешенной силой упругости пружины.
В динамике среди основных рассматриваются две задачи. Первая из них (прямая задача динамики) заключается в том, что по заданным механическим движениям и массой тела определяют силы, под действием которых осуществляются это движение. Вторая задача (обратная задача динамики) заключается в том, что по заданным силами, приложенными к телу, его массой и начальными условиями определяют движение которое они вызывают.
Конечно динамику принято делить на динамику материальной точки, динамику системы материальных точек и динамику твердого тела. В этом учебнике много положений и
теорем для точки и системы излагаются параллельно.
Законы Ньютона
В основе динамики лежат законы Ньютона, изложенные в «Математических началах
натуральной философии «.
Законы Ньютона являются объективными законами природы, установленными на основе
многочисленных опытов и наблюдений Ньютона и его предшественников. Эти законы истинные настолько, насколько выводы, вытекающие из них, согласуются с опытом в
пределах точности наблюдений. Системы координат, в которых справедливы
законы Ньютона, называются инерциальными. Инерциальными (Галилея) являются системы координат, движущихся поступательно, прямолинейно и равномерно относительно неподвижных звезд. С достаточной точностью инерциальной (основной) можно считать гелиоцентрическую систему координат при изучении движений со скоростями, малыми по сравнению со скоростью света. При решении многих задач по технике, основную систему координат (систему отсчета) связывают с Землей. При решении задач по астрономии, навигации и управления подвижными объектами, где приходится учитывать вращение Земли, за основную систему отсчета берут систему координат, связанную со звездами, то есть инерциальную систему координат.
Первый закон Ньютона (закон инерции)
Изолированная материальная точка сохраняет состояние покоя или равномерного и прямолинейного движения до тех пор; пока влияние со стороны других тел не выведет ее из этого состояния:
Изолированной называется материальная точка, взаимодействием которой с окружающими телами пренебрегают. Свойство изолированной материальной точки сохранять состояние равномерного и прямолинейного движения называется свойством инертности.
Из закона инерции следует, что спонтанное изменение движения материальной точки невозможно.
Движение материальной точки может измениться только в результате ее взаимодействия с другими телами. Мерой этих взаимодействий являются силы. Глубокий анализ внутреннего содержания понятия о механической силе сделал Ф. Энгельс. Введение понятия силы позволило установить связь между механическими и сложными немеханическими формами движения материи. Например, если рассматривать силу взаимодействия наэлектризованных частиц, то здесь оказывается связь между механическим движением и
более сложной формой движения, которое изучается в теории электричества. Величину и направление действия силы по наблюдаемым отклонениями движения материальной
точки от равномерного и прямолинейного движения подает второй закон Ньютона.
Второй закон Ньютона (основной закон динамики)
Скорость изменения количества
движения материальной точки равна силе, действующей на эту точку.
Математически этот закон выражается равенством:

где 

В классической механике рассматривают движение со скоростями, малыми по сравнению со скоростями света. При движении с большими скоростями, согласно формуле Лоренца,
масса будет зависеть от скорости движения:

где 


При малых скоростях 
Считая, 

где 
На основе (13.3) второй закон Ньютона можно сформулировать так: ускорение материальной точки пропорционально приложенной к ней силе и имеет одинаковые с ней направление.
Отметим, что такая формулировка второго закона Ньютона непригодна в динамике тела переменной массы. Если бы Ньютон сформулировал этот закон в форме (13.3) (а именно она применяется в большинстве учебников по общей физике), то была бы невозможной теория реактивного движения.
Уравнение (13.3) называется основным уравнением динамики свободной материальной
точки, или уравнением Ньютона. Второй закон Ньютона выражает количественное соотношение между тремя физическими величинами: силой, массой и ускорением. Понятие силы встречалось еще в статике, понятие ускорения — в кинематике. Массой материальной точки называется физическая величина, которая является мерой ее инертных и
гравитационных свойств.
Из физики известно, что силу можно измерить с помощью специального прибора —
динамометра, ускорение — одним из способов, указанных в кинематике. Массу можно
определить двумя способами.
Первый способ определения массы основывается на законе всемирного тяготения, согласно с которым сила взаимного притяжения между телами выражается формулой:

где 




Еще Галилей установил, что вблизи земной поверхности при свободном падении все тела
имеют одно и то же ускорение:

что равно 

Таким образом, измерив силу притяжения тела с помощью весов, можно по формуле
(13.6) определить его массу. То есть определение массы называется статическим, а
сама масса, определенная этим способом — гравитационной.
Второй способ определения массы состоит в следующем. Пусть одна и та же сила





по второму закону Ньютона:

Отсюда,

Взяв массу первого тела 


Это означает, что между первым и вторым законами Ньютона является полное соответствие, и они не включают в себя внутренних логических противоречий.
Третий закон Ньютона (закон равенства действия и противодействия}
Силы взаимодействия двух материальных точек или двух тел (действие и противодействие)
равны по величине, направлены в противоположные стороны и имеют общую линию действия. Если первый и второй законы Ньютона принадлежат к динамике материальной точки, то третий закон Ньютона принадлежит к динамике системы материальных точек или тел. Следует отметить, что действие и противодействие приложены к разным материальных точек или тел, и третий закон Ньютона, в отличие от первых двух, справедливый в любой
системе координат, а не только в инерциальной, он не содержит кинематических характеристик движения материальных объектов. В конце концов, третий закон Ньютона позволяет отличить реальные силы, приложенные к точкам, от фиктивных, которые могут появиться при математическом решении задач механики.
Закон независимости действия сил (принцип суперпозиции}. Ускорение материальной
точки, возникает при одновременном действии на нее нескольких сил, равно векторной сумме ускорений, которые предоставляют точке отдельные силы.
Этот закон следует из аксиомы о параллелограмме сил. Он не пригоден при воздействии на
материальную точку сил, зависящих от ускорение.
Во введении отмечалось, что законы Ньютона, как и все положения теоретической механики, основывается на них, носят ограниченный характер и является лишь первым приближением к действительности, хорошо согласуется с ней только при движениях с малыми скоростями. Эта ограниченность вызывается тем, что в теоретической механике свойства подвижных материальных объектов считают независимыми от свойств пространства и времени, которые в того же абсолютизируют. На самом деле пространство и время являются атрибутами движущейся материи, они накладывают определенный отпечаток на механические процессы, являющийся тем больше, чем ближе скорость движения тел в скорости света. В рамках своей применимости теоретическая механика занимает ведущее место среди естественных наук и имеет большое значение при исследовании механических процессов и явлений, встречающихся на практике. Законы Ньютона имеют также большое методологическое значение. Действительно, первый закон
Ньютона отражает в динамике принцип не уничтожения движения. Второй закон Ньютона
устанавливает зависимость между силой, массой и ускорением, позволяет решать конкретные задачи механики и тем самым значительно обогащает понятие силы. Третий закон Ньютона дает возможность глубже проникнуть в суть понятия силы. В нем сила выступает не односторонне, не только как действие, но и двусторонне как действие и противодействие, как взаимодействие между двумя материальными объектами.
Таким образом, согласно законам Ньютона, сила материальной категорией, ее
источниками являются физические тела, между которыми происходит взаимодействие, заключается в переносе механического движения из одного тела на другие, или в преобразовании энергии в движение.
Дифференциальные уравнения движения свободной материальной точки
Согласно трем способам задания движения точки (п 7.3) установим дифференциальное
уравнение ее движения. Если движение материальной точки массой 


В общем виде сила 
В природе редко встречаются силы, зависящие от ускорения. Примером силы, которая зависит от ускорения точки, может быть электромагнитная сила притяжения материальной точки в недвижимого центра, согласно закону Вебера, определяется выражением: 

Отметим, что искусственно, с помощью вычислителей, обратных связей и исполнительных устройств можно сформировать силы, которые зависят от любой производной перемещения во времени. Так, силы, которые явно зависят от времени, встречаются при исследовании работы различного рода машин и механизмов.
К силам, зависящим от положения точки (позиционных сил), относятся силы упругости, возникающие в упругих телах при их деформации, а также силы тяжести или отталкивания, возникающие при взаимодействии тел, имеющих электрические (магнитные) заряды.
Силы, которые зависят от скорости, встречаются при исследовании движения тел в вязкой среде (жидком или газообразном). В случае необходимости и те, и другие силы можно
сформировать искусственно с помощью обратных связей. Следовательно, уравнение (13.9) наберет вида:

Уравнению (13.10) в векторной форме соответствуют три скалярных дифференцируемых уравнения в координатной форме:

где 



каждое из дифференциальных уравнений (13.11) является уравнением второго порядка, система этих уравнений имеет шестой порядок. Уравнение (13.11) называются динамическими уравнениями движения материальной точки в координатной форме.
Если спроецировать обе части основного уравнения динамики (13.3) на натуральные оси (касательную 



Эти уравнения называются динамическими уравнениями движения точки в натуральной форме, или в форме Эйлера.
При решении задач механики вызывают интерес динамические уравнения движения материальной точки в проекциях на оси полярной системы координат. Эти уравнения получим, проектируя основное уравнение динамики (13.3) соответственно на радиальное (вдоль радиуса-вектора) и трансверсальное (перпендикулярное радиус-вектора) направления (7.53):

В случае цилиндрической системы координат (рис. 7.3) уравнение движения точки будет иметь следующий вид:

Наконец, для сферической системы координат (рис. 7.4), если воспользоваться выражениями для ускорений, приведенными в примере 7 п. 7.15, будем иметь:

Две основные задачи динамики свободной материальной точки
При исследовании движения материальной точки встречаются две основные задачи динамики (прямая и обратная).
Прямая или первая, основная задача
Определить равнодействующую сил F, действующих на материальную точку, если задано ее массу и кинематические уравнения движения.
Эта задача решается так.
1. Если движение материальной точки массой 

то дважды дифференцируя эти соотношения по времени, получим проекции ускорения
на оси координат, то есть:

Тогда на основании уравнения (13.11) определим проекции сил:

Следовательно, модуль равнодействующей силы:

Направление силы определим по направляющим косинусам:

2. Если движение материальной точки массой задано в натуральной форме, то по уравнениям (13.12) найдем проекции равнодействующей сил, действующих на материальную точку, на натуральные оси. Модуль силы и направление определим по формулам:

где 

3. Если движение материальной точки массой 

Обратная, или вторая, основная задача
Определить кинематические уравнения движения свободной материальной точки, если задано ее массу 




ибо порядок системы дифференциальных уравнений равен шести. Чтобы решить конкретную динамическую задачу, надо задать начальные условия движения для определения указанных постоянных интегрирования. Под начальными условиями движения материальной точки следует понимать значения координат точки и проекции ее скорости в начальный момент времени 

Аналогично начальные условия движения точки можно задать в векторной 


имеющие постоянные интегрирования. Если в (13.23) и в (13.25) подставить начальные условия движения точки (13.24), то получим систему из шести алгебраических уравнений с шестью неизвестными постоянными интегрирования, решая которую, найдем:

Наконец, подставив найденные значения постоянных интегрирования в соотношение (13.23),
выражающих общее решение системы дифференциальных уравнений (13.11), получим закон движения точки:

Рассматривая движение в натуральной форме, для решения обратной задачи динамики
применяют уравнения (13.12). Начальными условиями движения в этом случае имеет значение дуговой координаты при 
Общий интеграл первого из уравнений (13.12) имеет вид 
Вычисленную таким образом дуговую координату 
(13.12) и получим значение радиуса кривизны р траектории подвижной точки.
Итак, решение обратной задачи динамики материальной точки включает следующие операции:
1) составление динамических уравнения движения материальной точки согласно условию задачи;
2) интегрирование полученной системы дифференциальных уравнений, то есть нахождения общего решения этой системы;
3) определение соответствующих значений постоянных интегрирования;
4) нахождения закона движения.
Пример 1. Определить траекторию движения снаряда, выпущенного из ствола пушки с начальной скоростью 

Решение. В начальный момент 









Постоянные интегрирования 



Эти выражения являются также уравнением траектории в параметрическом виде. Изъяв время из этих уравнений, определим траекторию в явном виде:

Несложно увидеть, что траекторией снаряда является парабола, которая лежит в плоскости 




Поскольку 

Наибольшей высоты полета при заданном угле 

Очевидно, что наибольшее расстояние 


Пример 2. Найти закон свободного падения тел (задача Галилея).
Решение. Воспользуемся системой координат Oxyz (рис. 13.1). В этом случае 
При
При таких начальных условиях получим:
Поскольку тело падает вниз, то высоту падения нужно брать со знаком минус, то есть
Отсюда закон падения тел (по Галилею)
Время падения определяться по формуле
Задача решена.
Пример 3. Торпеда, которую выпустили с подводной лодки, которая находится на расстоянии h от морского дна, начинает двигаться со скоростью 
Решение. За координатную плоскость примем плоскость Oxyz (рис. 13.1). по условиям
задачи при
Силу сопротивления обозначим 


или
Система уравнений движения распадается на три независимых уравнения, общее решение которых будет:
Поскольку:
то, используя заданные начальные условия, получим:
и тогда решением будет:
Отметим, что из последних уравнений легко получить закон движения при отсутствии сопротивления среды (воды). Для этого нужно рассмотреть предел при 

Уравнения движения несвободной материальной точки
При формулировке основных задач динамики свободной точки считалось, что на движения
точкой не наложено никаких ограничений. Соответствующим выбором закона изменения силы 
Если на движение точки наложены определенные ограничения, то такое движение точки является несвободным. Например, если материальная точка (рис. 13.2) находится на конце недеформированного стержня длиной 

Вектор скорости точки всегда лежит в плоскости, касательной к сфере и построенной в
точке, которая совпадает в данный момент с материальной точкой.
Уравнение (13.28), таким образом, является уравнением сферической поверхности, которое образует связь. Итак, это уравнение связи.
Как уже отмечалось в начале курса в статике, ограничения, которые накладываются на
движение материальной точки, называют связями.
Ограничение движения точки может быть не только с помощью связи в форме поверхности,
но и в форме линий, с результатом пересечения двух поверхностей. Связи могут меняться
со временем, тогда их называют нестационарными. Можно привести примеры, когда ограничения заставляют точку двигаться только в определенной части пространства, тогда они будут записываться в форме неравенства. При наличии этих ограничений, которые называют связями на движение точки, независимо от действующих сил, координаты точки определенным образом связаны между собой и поэтому выбор начальных условиях не
может быть произвольным.
Итак, будем называть материальную точку несвободной, а ее движение — несвободным движением, если в результате тех или иных ограничений при воздействии на нее каких-либо сил она выполняет движение или по строго фиксированной линии, поверхности, или
находится в строго фиксированной части пространства.
При изучении несвободного движения точки применяют соответствующую аксиому об освобождении от связей, заменяя их действие соответствующими силами, называют реакциями связей. Тогда точку можно считать свободной, но такой, на которую действуют не только активные силы, но и пассивные — реакции связей.
Если обозначить через 
а через 

Векторном уравнению (13.29) можно поставить в соответствие три скалярных в проекциях на оси:

Особенностью этих уравнений является то, что в них реакции 
Рассмотрим методику решения задач динамики свободной точки в отдельных случаях, когда точка движется:
1) по идеально гладкой неподвижной поверхности;
2) по идеально гладкой неподвижной кривой.
Движение точки по гладкой неподвижной поверхности
Для изучения движения материальной точки по поверхности используем уравнение (13.30):

Эти уравнения включают шесть неизвестных: три координаты точки (x, y, z) и три неизвестные проекции 
Как уже отмечалось, координаты точки должны удовлетворять уравнению поверхности. это
дает четвёртое уравнения:

Конечно, четырех уравнений для определения шести неизвестных недостаточно. Для получения двух уравнений, которых не хватает, используем свойство связей и их идеальность.
Поскольку поверхность идеально гладкая, то это означает, что трение отсутствует, и реакция направлена по нормали n к поверхности.
Как известно, градиент функции

также является вектором, который направлен по нормали



Таким образом, уравнение (13.32) — (13.34) позволяют в принципе решить задачу о движении точки по гладкой поверхности. Заметим, что с уравнений (13.31) и (13.34) можно исключить реакции связей. для этого обозначим уровне отношение (13.34) через 

тогда:

и уравнение (13.31) будет выглядеть следующим образом:

Присоединяя к этим трем уравнениям четвёртое уравнения связи (13.32), получим систему четырех уравнений с четырьмя неизвестными

Вектор реакций связей 

Уравнение (13.37) называются уравнениями Лагранжа первого рода.
Движение точки по гладкой неподвижной кривой
Рассмотрим эффективность в этом случае уравнений Лагранжа первого рода и натуральных уравнений.
2.1. Уравнения Лагранжа первого рода. При движении точки по кривой уравнения связей имеют вид:

поскольку кривая образуется в следствии пересечения двух поверхностей, уравнения которых 


где 


Эти уравнения включают девять неизвестных: три координаты точки и шесть проекций
реакций связей.
Присоединяя к уравнениям (13.42) два уравнения связей (13.40) и условия идеальности
связей:

и

получим девять уравнений с девятью неизвестными. Из этих уравнений, как и в предыдущем случае, можно исключить проекции связей. Для этого отношения в выражениях (13.43) и (13.44) обозначим через 


Таким образом, уравнение (13.42) наберут вида:

Система (13.46) вместе с уравнениями связей (13.40) образует систему пяти уравнений с пятью неизвестными 



Модули этих реакций соответственно равны:

Пример 4. Рассмотреть движение тяжелой точки массой 

Решение. Совместим начало координат (Точку О) с любой точкой оси цилиндра, направим ось 


Примем, что в начальный момент (при 
то есть начальная скорость направлена параллельно оси Oz.
На материальную точку действуют сила тяжести 

откуда
Проекции сил определяются выражениями:
Подставив эти выражения для сил в уравнение (13.31), получим:

С третьего уравнения (1), после интегрирования при заданных начальных условиях, получим
то есть расстояние от начальной плоскости Оху возрастает пропорционально времени.
Умножив первое уравнение (1) на 

найдем:

Умножив первое уравнение (1) на 


Перейдем теперь к цилиндрическим координатам по формулам:
Поскольку
то уравнения (2) и (3) будут выглядеть так:
или

и

Перепишем уравнение (4) в форме:
тогда после интегрирования получим:
Поскольку при 


С этого уравнения видно, что при выбранных начальных условиях движение точки будет происходить в области, где 
Подставив выражение (6) в уравнение (5), получим:
В соответствии формуле (13.36), получим:
Модуль реакции:
Реакция равна нулю при 



Это будет сделано в следующем разделе.
Натуральные уравнения движения по кривой
Покажем, что применение натуральных уравнений при движении точки по кривой является значительно эффективным и не требует таких громоздких преобразований, которые имеют место при применении уравнений Лагранжа первого рода.
Действительно, уравнения движения точки по кривой является по определению несвободным и в проекциях на оси натурального трехгранника имеют вид:

Подставив в (13.49) выражения для проекций ускорения, получим:

Уравнение (13.50) называются натуральным уравнениями движения. С третьего уравнения следует, что бинормальная составляющая реакции 
При заданных активных силах и известных уравнениях связей (13.40) уравнение (13.49) позволяют определить закон движения точки и реакции связей. Заметим, что между проекциями реакции 
Так, при движении точки по шершавой кривой проекция 

где 
Сила трения скольжения всегда направлена противоположно скорости, поэтому:

Если движение точки происходит по идеально гладкой поверхности, то 

Как видно из уравнений (13.53), в этом случае первое уравнение служит для определения закона движения, а второе и третье — для определения реакции связи. При движении точки по плоской, неподвижной шероховатой кривой уравнения (13.50) записывается в форме:

Пример 5. Используя уравнения (13.53), исследовать движение математического маятника (рис. 13.5). (Математическим маятником называется материальная точка, которая движется под действием силы веса по гладкому кругу, расположенного в вертикальной плоскости).
Решение. Реализуем заданное движение точки по гладкому кругу, подвесив материальную
точку массой 
точке О (рис. 13.5) При этом начальная скорость подвешенной точки будет располагаться в
вертикальной плоскости Оху перпендикулярно радиусу. Такая конструкция маятника реализует движение точки по гладкому кругу (так как трение отсутствует).
Положение точки определяем углом 
масса точки 




точки будут:
Соответствующие проекции силы на направление нормали 

Реакция 
Радиус кривизны 

поскольку:
Перепишем последние уравнения в следующем виде:


Как видим, уравнение (1) служит для определения закона движения маятника, а уравнения (2) — для определение реакции нити. Пусть в начальный момент 



Согласно уравнению (2) для определения реакции 



запишем уравнение (1) в виде уравнения с раздельными переменными:
Учитывая начальные условия 
Отсюда получим:

Определив 
Если учесть, что 

Исследуем полученный решение (4). Найдем такие параметры движения, в частности угол 

Отсюда имеем:
Если поставить условие, чтобы связь была удерживающей при любом угле, даже при верхнем вертикальном положении нити 
при этом маятник выполнять круговое движение. В частности, при 
Если начальная скорость 


Следовательно , в течение всего движения должны выполняться неравенства 


Перейдем к определению закона движения маятника
Обозначив в уравнении (1) 



дифференциальными уравнениями свободных прямолинейных колебаний, которые мы рассматривали в кинематике простейших движений.
Следовательно, угол 

а амплитуда колебаний:
Как видим, при малых колебаниях период не зависит от начального отклонения 


В разделе нелинейных колебаний покажем, что на самом деле колебания математического маятника не есть изохронными, потому что их период зависит от амплитуды колебаний.
На этом завершим исследования математического маятника.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИЗУЧЕНИЕ ЗАКОНОВ КИНЕМАТИКИ И ДИНАМИКИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА НА МАШИНЕ АТВУДА
ЛАБОРАТОРНАЯ РАБОТА ПО МЕХАНИКЕ № 2
для студентов естественных факультетов и физико-технического института
Печатается по решению кафедры общей физики: протокол № 3 от 27 декабря 2012 г.
Составители: к.ф.-м.н., доц. Акманова Г.Р. асс. Шафеев Р.Р.
2
Лабораторная работа № 2 ИЗУЧЕНИЕ ЗАКОНОВ КИНЕМАТИКИ И ДИНАМИКИ
ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА НА МАШИНЕ АТВУДА
Приборы и принадлежности: установка ФМ 11 (машина Атвуда),
блок электронный, набор грузов. Цель работы: 1. Изучение законов кинематики и динамики
равноускоренного поступательного движения.
2.Экспериментальное определение ускорения движения.
3.Определение теоретического значения ускорения движения.
КРАТКАЯ ТЕОРИЯ
Механическое движение – простейшая форма материи, которое состоит в перемещении тел или их частей относительно друг друга в пространстве с течением времени. В общем случае движение тел или их частей может иметь довольно сложный характер. Для того, чтобы задать движение тела, нужно сначала изучить законы движения отдельных частиц тела. Любое тело можно представить как систему материальных точек. В механике применяется абстракция реального тела – абсолютно твердое тело (или просто твердое тело). Абсолютно твердым называется тело, в котором отдельные части не перемещаются друг относительно друга, т.е. абсолютно твердое тело можно рассматривать как систему материальных точек, расстояние между которыми неизменно (тело не деформируется).
Любое сложное движение твердого тела сводится к простым движениям: поступательному и вращательному. Поступательным называется такое движение тела, при котором любая прямая, проведенная в теле, сохраняет свое направление неизменным пространстве. При поступательном движении все точки твердого тела описывают одинаковые траектории и имеют одинаковые перемещения, скорости и ускорения. Поэтому для задания поступательного движения твердого тела достаточно знать законы движения одной его точки (центра масс).
3

x at2
2
Движение тела (точки) уравнениями. Кинематически
известен его радиус — вектор r
кинематическими динамическими движение тела будет задано, если
как функция от времени t:
либо декартовы координаты x, y, z как функция t:
Уравнения (1) и (2) называются кинематическими уравнениями движения тела (точки). В случае равнопеременного движения вдоль оси x (y=0,z=0) уравнение (2) для x имеет вид:
|
x 0t |
at2 |
|
|
(3) |
||
|
2 |
||
где 0 — начальная скорость тела,
а — ускорение.
Если 0 =0, то (3) переходит в
(4)
Уравнение динамики движения записывается на основании второго закона Ньютона: «Изменение импульса тела пропорциональна движущей силы и происходит по направлению той прямой, по которой эта сила действует»:
|
d Fdt |
(5) |
|
|
где m |
— импульс тела, |
|
|
F Fi |
— результирующая всех действующих сил, |
|
|
dt — время действия силы, |
Fdt — импульс силы. Из (5) получим
4
|
d |
||
|
F |
(6) |
|
|
dt |
В виде (5) и (6) второй закон Ньютона справедлив и в релятивистской механике. Если m=const, то (6) примет вид:
|
d(m ) |
d |
||||||
|
F |
m |
ma |
(7) |
||||
|
dt |
dt |
||||||
Для определения характера движения и изучения зависимости ускорения системы грузов от их масс используется машина Атвуда (рис. 1). Она состоит из укрепленного на штативе 1 шкива 2 радиуса R, через который перекинута нить с подвешенными на ней одинаковыми грузами 3 и 4. Масса этих грузов может быть увеличена добавочными небольшими грузами (перегрузками) 5.
Рис.1. Машина Атвуда
Система приводится в движение за счет добавочного груза 5 массой m0. Шкив 2 вращается вокруг оси с малым трением, т. е. можно считать, что движение грузов равнопеременное. Ускорение грузов определяют
5
по времени поворота шкива t на определенный угол . Угловое ускорениешкива:
2
t2
Ускорение грузов:
a R 2 R t2
Ускорение a, путь S и время движения t при равнопеременном движении связаны соотношением:
При таком движении ускорение постоянно a=const и не зависит от пути S. Таким образом, если при равнопеременном движении груза шкив совершает один полный оборот ( =2 ) за время t1, два полных оборота ( =4 ) за время t2, то из выражения (9) следует критерий равнопеременности движения:
|
t |
2 |
2 |
||
|
2 |
(11) |
|||
|
t |
||||
|
1 |
Найдем закон движения грузов. Обозначим через m — массу груза 3. Тогда масса груза 4 с добавочным грузом 5 есть величина, равная m + m0. На правый груз действуют две силы: сила тяжести (m +m0)g и сила натяжения нити T4. Их равнодействующая вызывает движение груза с ускорением а. По второму закону Ньютона сила F, действующая на правый груз, равна произведению массы m на ускорение а:
Результирующая сила равна векторной суммесил, действующих на
платформу: F Fi .
Проектируя вектор сил и вектор ускорения на осьОХ получаем:
m m0 a m m0 g T4 (13)
6
где g = 9,8 м/с2 – ускорение свободного падения тела.
Если предположить, что нить нерастяжима, то ускорение груза 3 равно (-a). Тогда для груза 3 получим:
|
ma mg T3 |
(14) |
||
|
Момент инерции шкива 2 мал (J = 0), тогда силы натяжения нити |
|||
|
равны |
|||
|
Т3 = Т4. Из (13) и (14) получаем выражение: |
|||
|
m m0 a m m0 g ma mg |
|||
|
или |
|||
|
m0 |
|||
|
a |
g |
(15) |
|
|
2m m0 |
Из второго закона Ньютона вытекают два следствия. Если на тело постоянной массы m действовать различными силами F1 и F2, то согласно второму закону Ньютона, тело будет двигаться с разными ускорениями a1 и a2, отношение которых равно отношению сил:
|
a1 |
F1 |
|||
|
a2 |
(16) |
|||
|
F2 |
при m=const.
Из уравнения (12) следует, что если к телам с различными массами m1 и m2 приложить равные силы, то тела будут двигаться с разными ускорениями a1 и a2, отношение, которых обратно пропорционально отношению масс:
|
a1 |
m2 |
||
|
a2 |
(17) |
||
|
m1 |
при F =const.
7
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
Экспериментальная установка — машина Атвуда представлена на рис.1.Основание снабжено тремя регулируемыми опорами и зажимом для фиксации вертикальной стойки. Вертикальная стойка выполнена из металлической трубы, на которую нанесена миллиметровая шкала, и имеет визир.
На верхнем кронштейне размещается узел подшипников с малоинерционным шкивом, через который перекинута капроновая нить с двумя основными грузами и набором разновесов, электромагнитный тормоз, предназначенный для фиксации исходного положения грузов. Нижний кронштейн имеет зажим для крепления на вертикальной стойке и элементы фиксации фотодатчика. Установка работает от блока электронного.
Для проведения измерений необходимо перекинуть через блок 2 нить с двумя грузами 3 и 4 и убедиться, что система находится в положении безразличного равновесия. Установить кронштейн с фотодатчиком 6 в нижней части шкалы вертикальной стойки, а фотодатчик расположить таким образом, чтобы правый груз при движении вниз проходил в центре рабочего окна фотодатчика (за нижнее положение груза берется риска шкалы, соответствующая риске на корпусе фотодатчика и являющаяся как бы продолжением оптической оси фотодатчика, которую пересекает движущийся груз).
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Упражнение 1.
Экспериментальное определение ускорения движения
1.Нажать кнопку «СЕТЬ», находящуюся на задней панели блока электронного.
2.Установить правый груз в крайнем верхнем положении.
3.Положить на правый груз один из добавочных грузов 5 массой
10 г.
4.Нажать на кнопку «ПУСК » блока. Происходит растормаживание электромагнита, правый груз начинает опускаться, и таймер блока
начинает отсчет времени. При пересечении правым грузом оптической оси фотодатчика отсчет времени прекратится.
8

Записать показания таймера, т. е. время движения грузов.
5.Определить по шкале пройденный грузом путь S, как расстояние от нижней плоскости груза (в верхнем положении) до оптической оси фотодатчика.
6.Не меняя первоначальной высоты груза, повторить опыт 5 раз. Найти среднее время движения t.
7.Определить значение ускорения движения груза по формуле:
2S
aэксп. t2 .
8. Определить ускорение свободного падения по формуле:
g aэксп. 2m m0 , m0
где m = 50 г – масса основного груза, m0 – масса добавочного груза.
9.Оценить относительные и абсолютные погрешности величин ускорения a и ускорения свободного падения g.
10.Повторить измерения и вычисления согласно пп. 3 – 9 с добавочным грузом массой 20 г.
Упражнение 2.
Определение теоретического значения ускорения
1.Определить теоретическое значение ускорения движения груза по формуле:
2.Сравнить теоретическое и экспериментальное значения ускорения движения груза.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Дайте определение механического движения. Какое движение называется поступательным? Вращательным?
2.Какое тело называется абсолютно твердым?
3.Дайте определения физических понятий: системы отсчёта,
9
радиусавектора, скорости, ускорения.
4.Какое движение называется равноускоренным? Каким образом связаны между собой путь, время и скорость прямолинейного равноускоренного движения?
5.Сформулируйте и запишите второй закон Ньютона. Какие следствия вытекают из второго закона Ньютона.
6.В каких системах отсчета справедливы законы Ньютона?
7.Что характеризует масса тела?
8.Каким образом из экспериментальных данных определяется ускорение движения грузов?
9.Как изменится ускорение системы, если увеличить массу основного груза m , не меняя массы перегрузка?
ЛИТЕРАТУРА
1.Стрелков С.П. Механика. — СПб: Изд-во «Лань», 2005, § 2-11, 16-21.
2.Сивухин Д.В. Общий курс физики. Т.1. Механика, — М: ФИЗМАТЛИТ; Изд-во МФТИ, 2006, § 2-4, 9-12.
3.Савельев И.В. Курс общей физики. Кн.1. Механика.- СПб: Изд-во
«Лань», 2007,§ 1.1-1.5, 2.2 – 2.6.
4.Иродов И.Е. Механика. Основныезаконы. – М.:БИНОМ.
ЛабораторияЗнаний, 2010, §1.1 -1.3, 2.1– 2.4.
10
Соседние файлы в папке Gmail
- #
- #
- #
- #
- #
- #
- #
- #
ГЛАВА1
КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ И
ПРОСТЕЙШИХ СИСТЕМ
1.1. Теоретический материал
Физическая величина – это количественная характеристика свойства материальных объектов или явлений (процессов). Каждая физическая величина устанавливается однозначным способом ее измерения – экспериментального определения или расчета. Определение физической величины указывает принципиальный способ ее измерения.
Физическое понятие (модель объекта или явления) – это абстракция (филос.), которая отражает только основные, наиболее существенные, свойства материальных объектов или явлений (процессов).
Критерий правильности выбора модели. Если в данной задаче физическая величина, описывающая неосновное свойство, от которого мы абстрагируемся, много меньше другой, характерной для этой задачи, величины той же размерности, то модель выбрана верно.
Заметим, что один и тот же материальный объект или одно и то же явление в различных условиях могут быть рассмотрены в рамках различных моделей, если они удовлетворяют критериям правильности выбора этих моделей.
Тело отсчета – тело, относительно которого рассматривается движение других тел.
Часы – неподвижный относительно тела отсчета прибор для измерения времени, принцип действия которого основан на сравнении длительности исследуемого временного интервала с длительностью выбранного за эталон периодического процесса.
Система отсчета – совокупность системы координат[1], связанной с телом отсчета, и набора синхронизированных часов, размещенных в разных точках координатной системы.
Условие синхронизации часов A и B, расположенных в разных точках системы отсчета (в предположении об изотропности пространства):
(1.1)
Здесь – момент времени излучения из точки A светового сигнала (кванта света) по часам в точке A, – момент времени регистрации этого сигнала в точке B по часам в точке B, – момент времени регистрации в точке A отраженного в точке B сигнала по часам в точке A.
Материальная точка – физическое понятие (модель, абстракция), представляющее тело, размерами (и формой) которого можно пренебречь в условиях данной задачи.
Положение материальной точки относительно данной системы отсчета (в данной системе отсчета) S задается ее координатами или радиус-вектором .
Радиус-вектор материальной точки относительно данной системы отсчета – вектор, начало которого находится в начале координат этой системы, а конец – в месте расположения материальной точки (см. рис. 1.1а):
, (1.2)
где , и – орты декартовой системы координат: , , ; x, y, z – координаты материальной точки.
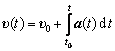 |
Закон движения материальной точки относительно данной системы отсчета – зависимость радиус-вектора или координат материальной точки от времени:
(1.3)
Траектория движения материальной точки – линия, описываемая в пространстве концом радиус-вектора материальной точки.
Уравнение траектории задается совокупностью двух уравнений
(1.4)
которые можно получить, исключая время из закона движения в координатной форме (1.3). Заметим, что сам закон движения в координатной форме представляет собой уравнение траектории, заданное в параметрическом виде.
Перемещение материальной точки – изменение радиус-вектора материальной точки за время Dt с момента времени t (рис. 1а):
. (1.5)
Скорость материальной точки относительно данной системы отсчета – физическая величина, равная производной радиус-вектора материальной точки по времени (производная берется при постоянных ортах системы координат, поскольку они жестко связаны с телом отсчета):
, (1.6)
где , , – проекции скорости на соответствующие оси системы координат. Скорость можно представить в виде суммы составляющих скорости вдоль осей системы координат:
. (1.7)
При этом модуль скорости равен
. (1.8)
В соответствии с определением скорость всегда направлена по касательной к траектории (см. рис. 1.1б).
Зная закон изменения скорости материальной точки , и радиус-вектор в начальный момент времени t0, можно найти закон движения:
. (1.9)
Путь s(t), пройденный материальной точкой вдоль траектории (длина траектории) за время t, равен
, (1.10)
при этом модуль скорости в любой момент времени равен
. (1.11)
Ускорение материальной точки относительно данной системы отсчета – физическая величина, равная производной скорости материальной точки по времени (при постоянных ортах системы координат):
, (1.12)
где ax, ay, az – проекции ускорения на соответствующие оси системы координат. Ускорение можно представить в виде суммы составляющих ускорения вдоль осей системы координат:
. (1.13)
При этом модуль ускорения равен
. (1.14)
Зная закон изменения ускорения материальной точки , а также скорость и радиус-вектор в начальный момент времени t0, можно найти закон изменения скорости и закон движения:
, (1.15)
. (1.16)
Начальные условия для материальной точки – значения радиус-вектора и скорости в начальный момент времени t0 относительно заданной системы отсчета:
(1.17)
Тангенциальное ускорение – составляющая ускорения вдоль направления скорости (см. рис. 1.2):
, , , (1.18)
, (1.19)
где – проекция ускорения на направление скорости .
Движение материальной точки при – ускоренное, при – замедленное, при – равномерное, а при – равнопеременное.
Нормальное ускорение – составляющая ускорения , перпендикулярная направлению скорости (рис. 1.2):
, , , (1.20)
где – проекция ускорения на направление , перпендикулярное скорости и направленное к центру кривизны траектории.
Нормальное ускорение всегда направлено к центру кривизны траектории – центру окружности максимального радиуса (радиуса кривизны траектории), касательной к траектории в данной точке, при этом
, (1.21)
где – радиус кривизны траектории в данной точке, а – угол между скоростями в моменты времени t и t + dt.
Ускорение можно представить в виде суммы нормального и тангенциального ускорений:
. (1.22)
При этом модуль ускорения равен
. (1.23)
В соответствии с (1.21) и (1.22) ускорение всегда отклонено от направления скорости в сторону центра кривизны траектории в данной точке, то есть внутрь траектории (см. рис. 1.2).
В частном случае движения материальной точки по окружности, т.е. движения в плоскости по траектории с постоянным радиусом кривизны – (рис. 1.3), можно ввести угловую скорость и угловое ускорение :
(1.24)
При этом:
(1.25)
Механическая система – совокупность материальных тел.
Система материальных точек – совокупность тел, каждое из которых можно считать материальной точкой. Далее будем считать, что всякую рассматриваемую нами механическую систему можно рассматривать как систему материальных точек.
Абсолютно твердое тело – тело (система материальных точек), расстояния между двумя любыми материальными точками которого не меняются в условиях данной задачи.
Поступательное движение абсолютно твердого тела – движение, при котором прямая, соединяющая любые две материальные точки тела, перемещается параллельно самой себе.
Принцип суперпозиции движений – в случае поступательного движения системы отсчета S¢ относительно системы S (рис. 1.4) радиус-вектор (скорость, ускорение) произвольной материальной точки относительно системы S равен сумме радиус-векторов (скоростей, ускорений) начала отсчета O’ системы S’ и той же материальной точки относительно системы S’:
(1.26)
Здесь и – переносные скорость и ускорение соответственно.
Уравнения кинематической связи – уравнения, связывающие кинематические характеристики различных тел системы:
(1.27)
Существуют два способа нахождения уравнений кинематической связи.
Способ 1. Принцип независимых перемещений. Перемещение какого-либо тела в системе связанных тел складывается из так называемых «независимых» перемещений, каждое из которых обусловлено (вызвано) перемещением соответствующего другого тела системы при покоящихся остальных телах:
. (1.28)
Способ 2. Записать величины постоянных кинематических характеристик элементов связей (нитей, штанг, блоков, поверхностей и т.д.) через координаты тел системы, используя свойства этих элементов (нерастяжимость, неподвижность, недеформированность), и продифференцировать эти величины по времени.
1.2. Основные типы задач и методы их решения
1.2.1. Классификация задач кинематики
Основной задачей кинематики является определение кинематических характеристик тел, движущихся относительно данной системы отсчета.
Большинство задач кинематики можно условно отнести к следующим типам задач или их комбинациям:
1) кинематика материальной точки,
2) принцип суперпозиции движений,
3) уравнения кинематической связи,
4) кинематика простейших механических систем.
Как правило, один из типов задач имеет основное, другие – подчиненное по отношению к условию задачи значение.
1.2.2. Общая схема решения задач кинематики
I. Определиться с моделями материальных объектов и явлений.
1. Нарисовать чертеж, на котором изобразить рассматриваемые тела.
2. Выбрать систему отсчета и изобразить на чертеже ее систему координат (из соображений удобства).
3. Изобразить и обозначить кинематические характеристики тел.
4. Выбрать модели тел и их движения (если это не сделано в условии задачи).
II. Записать полную систему уравнений для искомых величин.
1. Записать в проекциях на оси координат:
а) законы движения,
б) законы изменения скорости,
в) законы изменения ускорения.
2. Записать начальные условия.
3. Записать уравнения кинематических связей.
4. Использовать результаты ранее решенных задач и особые условия задачи (например, заданные соотношения между характеристиками системы).
III. Получить искомый результат в аналитическом и численном видах.
1. Решить систему полученных уравнений.
2. Провести анализ решения (проверить размерность и лишние корни, рассмотреть характерные случаи, установить область применимости).
3. Получить численный результат.
Примечания.
В случае решения задач на кинематику материальной точки в пп. I.3 – II.2 речь идет о кинематических характеристиках материальной точки, а п. II.3 надо опустить.
В случае решения задач на кинематику простейших механических систем в пп. I.3 – II.2 речь идет о кинематических характеристиках тел рассматриваемой системы.
Пункты II.1 – II.3 (в том числе II.2.a – II.2.в) можно выполнять в той или иной последовательности в зависимости от типа задачи.
1.3. Примеры решения задач
Задача 1.1
(Кинематика материальной точки)
Скорость материальной точки зависит от ее положения в декартовой системе координат следующим образом: , где c и b – положительные постоянные величины. В начальный момент времени радиус-вектор материальной точки равен нулю: . Определить:
а) законы движения , изменения скорости и ускорения , тангенциальную и нормальную проекции ускорения;
б) уравнение траектории y(x) материальной точки;
в) радиус кривизны траектории ;
г) угол между скоростью и ускорением .
Решение
Следуем общей схеме решения задач кинематики материальной точки и простейших систем.
I. По условию задачи движение происходит в плоскости XY, образованной координатными осями, направления которых заданы ортами и .
II. Запишем начальные условия и закон изменения скорости тела в проекциях на оси выбранной системы координат:
(1.29)
(1.30)
III. Записанные дифференциальные уравнения относительно координат материальной точки (1.29) с учетом начальных условий (1.29) позволяют найти закон движения материальной точки в проекциях на оси координат и зависимость от времени радиус-вектора :
(1.31)
. (1.32)
Используя найденную зависимость x(t) (1.31), определим закон изменения скорости и закон изменения ускорения :
, (1.33)
. (1.34)
Уравнение траектории находится из закона движения материальной точки путем исключения из (1.31) времени t:
. (1.35)
Остальные искомые величины определяются в соответствии с формулами, приведенными в п. 1 данной Главы.
Модуль скорости (1.7) равен:
. (1.36)
Проекции ускорения и (1.19, 1.23) получим в виде:
(1.37)
Радиус кривизны траектории (1.21) равен:
. (1.38)
Угол между скоростью и ускорением определяется соотношением:
. (1.39)
Заметим, что материальная точка движется по параболической траектории (1.35) с постоянным ускорением, направленным вдоль оси Y (1.34). На рис. 1.5 схематично изображена траектория движения материальной точки и изображены векторы ускорения и начальной скорости.
Нетрудно видеть, что при решения соответствуют начальным условиям задачи. При этом тангенциальное ускорение в указанный момент времени равно нулю, радиус кривизны траектории в данный момент времени , а угол между скоростью и ускорением .
При значения координат точки и модуль скорости, как и следовало ожидать, неограниченно возрастают, нормальное ускорение и угол между скоростью и ускорением стремятся к нулю, а радиус кривизны траектории – к бесконечности.
Задача 1.2
(Кинематика материальной точки)
Находящееся на высоте H над Землей тело бросили горизонтально с начальной скоростью . Найти закон движения тела, уравнение траектории, законы изменения скорости и ускорения, а также нормальную и тангенциальную проекции ускорения и радиус кривизны траектории в произвольный момент времени.
Решение
I. Нарисуем чертеж и изобразим на нем заданную в условии задачи скорость тела в начальный момент времени (t = 0) и предполагаемую траекторию движения тела (рис. 1.6).
Выберем систему отсчета, связанную с Землей. Ось X декартовой системы координат направим горизонтально вдоль поверхности Земли по направлению начальной скорости , а ось Y – вертикально вверх на положение тела в начальный момент времени. Будем считать, что тело является материальной точкой, а движение тела у поверхности Земли происходит с постоянным ускорением свободного падения .
II. В соответствии с выбранной системой отсчета и выбранными моделями тела и его движения запишем начальные условия и закон изменения ускорения тела в проекциях на оси координат:
(1.40)
(1.41)
III. Записанные дифференциальные уравнения относительно проекций скорости материальной точки с учетом начальных значений позволяют найти закон изменения скорости тела и закон его движения в проекциях на оси координат:
(1.42)
(1.43)
Уравнение траектории находится из закона движения тела в координатной форме (1.43) путем исключения времени t:
. (1.44)
Остальные искомые величины определяются в соответствии с формулами, приведенными в п. 1 данной Главы.
Модуль скорости (1.8) равен:
. (1.45)
Модуль ускорения (1.14) имеет вид:
. (1.46)
Проекции ускорения на направление скорости и перпендикулярное ему направление (1.19, 1.23) равны:
, . (1.47)
Радиус кривизны (1.21) определяется соотношением:
. (1.48)
Заметим, что в данной задаче все формулы для нахождения искомых величин справедливы с начального момента времени t0 = 0 до момента падения тела на Землю t0 £ t£ tпад. Этот момент времени легко найти из закона движения (1.43), приняв координату y равной нулю:
. (1.49)
Задача 1.3
(Кинематика материальной точки и принцип
суперпозиции движений)
Лодка пересекает реку с постоянной относительно воды скоростью , перпендикулярной направлению течения реки. Модуль скорости течения реки, ширина которой d, нарастает от берегов к середине реки по параболическому закону, изменяясь от 0 до um. Найти уравнение траектории лодки, время ее движения , а также снос лодки l вниз по течению от места ее отплытия до места причаливания на противоположном берегу реки.
Решение
I. Выберем декартову систему координат, жестко связанную с берегом реки, и с началом в месте отплытия лодки. Оси системы координат и скорость течения реки изображены на рис. 1.7.
При решении задачи лодку будем считать материальной точкой, а берега реки параллельными.
II. Запишем начальные условия для лодки в соответствии с условиями задачи:
(1.50)
где , – проекции скорости лодки на оси выбранной системы координат.
В соответствии с принципом суперпозиции движений (1.26) в любой момент времени или в проекциях на оси координат:
(1.51)
По условию задачи модуль скорости течения реки, ширина которой d, нарастает от берегов к середине реки по параболическому закону, поэтому можно записать:
, (1.52)
где и – постоянные величины. Для определения величины используем условие задачи:
. (1.53)
Используя начальные условия и соотношение (1.53), получим величину a:
. (1.54)
III. Система уравнений (1.51) с учетом (1.52) – (1.54) преобразуется к виду:
(1.55)
Интегрируя уравнения (1.55) с учетом начальных условий для координат лодки (1.50), находим закон движения:
, (1.56)
. (1.57)
Уравнение траектории получаем, исключая время t из закона движения в координатной форме (1.56) и (1.57):
. (1.58)
Поскольку в момент причаливания , время движения лодки равно:
. (1.59)
Следовательно, для искомого сноса лодки l получим (см. 1.58):
. (1.60)
Задача 1.4
(Принцип суперпозиции движений)
Определить форму траектории капель дождя на боковом стекле трамвая, движущегося горизонтально со скоростью , во время его торможения с ускорением . Капли дождя падают на землю вертикально вниз, и скорость их относительно земли постоянна и равна .
Решение
I. Нарисуем чертеж и изобразим на нем заданные в условии задачи кинематические характеристики капли дождя и трамвая в момент начала торможения трамвая (рис. 1.8).
Выберем систему координат XY, связанную с Землей, так, чтобы ось X была направлена горизонтально вдоль ускорения трамвая, а ось Y – вертикально вниз. Выберем также вторую систему координат X¢Y¢, связанную со стеклом трамвая, так, чтобы ее оси X¢ и Y¢ были сонаправлены с осями X и Y. Время в обеих системах отсчитываем от момента начала торможения трамвая.
Будем считать, что капля дождя является материальной точкой, положение которой в момент начала торможения трамвая совпадает с началом координат системы X¢Y¢.
II. Используя принцип суперпозиции движений (1.26), запишем скорость и ускорение капли дождя относительно стекла трамвая (системы координат X¢Y¢):
, (1.61)
. (1.62)
В соответствии с выбранной системой отсчета запишем начальные условия для капли дождя:
, (1.63)
, (1.64)
III. Записанные дифференциальные уравнения (1.61) и (1.62) с учетом начальных условий (1.63) и (1.64) позволяют найти закон движения капли в проекциях на оси координат:
(1.65)
Уравнение траектории находится из закона движения капли путем исключения из (1.65) времени t:
. (1.66)
Как видим, траектория в системе координат X¢Y¢, связанной со стеклом трамвая, является параболой (см. рис. 1.9) с вершиной в точке с координатами:
, . (1.67)
Задача 1.5
(Уравнения кинематической связи)
Концы твердого стержня MN могут свободно скользить по сторонам прямого угла MON (см. рис. 1.10). Найти уравнение траектории точки P стержня, которая делит его на части длиной а и b.
Решение
I. Выберем и изобразим декартову систему координат, оси которой совпадают со сторонами угла MON (см. рис. 1.10).
В соответствии с условием задачи будем считать стержень абсолютно твердым. Следовательно, его положение в любой момент времени t однозначно задается углом j(t) между осью OX и стержнем MN.
II. Запишем закон движения точки P стержня в координатной форме (см. рис. 1.10):
(1.68)
Искомое уравнение траектории точки P можно получить, исключив время из закона движения (1.68).
III. Преобразуя уравнения (1.68), получаем:
. (1.69)
Следовательно, искомое уравнение траектории принимает вид:
. (1.70)
Уравнение (1.70) является уравнением эллипса с полуосями, совпадающими по направлению с осями выбранной системы координат и равными a и b. В случае, когда a = b, эллипс вырождается в окружность.
Задача 1.6
(Уравнения кинематической связи)
На клине с углом при основании a, расположенном на горизонтальной поверхности, находится система двух тел 1 и 2 (см. рис. 1.11), связанных нерастяжимой нитью, перевешенной через маленький блок, ось которого закреплена в верхней точке клина. Записать уравнение кинематической связи для ускорений клина и двух тел, если тело 2 не отрывается от вертикальной поверхности клина в процессе движения.
Решение
I. Выберем систему отсчета, связанную с горизонтальной поверхностью. Ось X декартовой системы координат направим горизонтально, а ось Y вертикально вверх (см. рис. 1.11).
Будем считать тела 1 и 2 материальными точками, связанными нерастяжимой нитью, а клин – абсолютно твердым телом, которое может двигаться поступательно вдоль оси X. Обозначим координаты первого и второго тел в системе координат XY – (x1, y1) и (x2, y2), соответственно. Линейные размеры блока по условию задачи малы по сравнению с длиной нити, поэтому не будем учитывать их при записи уравнений кинематической связи для координат тел системы.
II. Выразим длину нити l через вертикальные координаты различных точек рассматриваемой системы тел:
, (1.71)
где – координата блока, не изменяющаяся в процессе движения.
Если длину наклонного участка нити выразить через горизонтальные координаты тел системы, то выражение для длины нити принимает вид:
. (1.72)
III. Дифференцируя (1.71) и (1.72) дважды по времени и учитывая, что и , получаем искомые уравнения кинематической связи для ускорений тел рассматриваемой системы:
(1.73)
Задача 1.7
(Уравнения кинематической связи)
Система тел состоит из двух блоков и двух подвешенных к ним тел (см. рис. 1.12). Один из блоков составлен из двух коаксиальных цилиндров с неподвижной относительно потолка осью, имеющих различные радиусы r и R. Первое тело подвешено на нити, намотанной на цилиндр радиуса r, второй – на нити, прикрепленной к оси другого блока. Найти ускорение второго тела, если известно, что ускорение первого тела равно a1. Нити считать нерастяжимыми.
Решение
I. Выберем систему отсчета, жестко связанную с потолком. Направление осей декартовой системы координат, связанной с телом отсчета, показано на рис. 1.12.
Считаем тела 1 и 2 материальными точками, нити – нерастяжимыми. Проскальзывания нитей относительно блоков нет.
II. Пусть за малый интервал времени Dt изменение координаты первого тела равно Dx1 (для определенности будем считать, что оно опускается). Поскольку нить нерастяжима, то угол поворота Dj цилиндра радиусом r связан с величиной Dx1 следующим соотношением:
. (1.74)
При этом второй цилиндр радиусом R повернется на тот же угол Dj, а длина нити, на которой лежит блок с подвешенным к нему телом 2, изменится на величину:
. (1.75)
Изменение координаты центра второго блока, а значит и второго тела, равно:
. (1.76)
III. Решая систему уравнений (1.74) – (1.76), получим уравнение, связывающее изменения координат двух тел:
. (1.77)
Поделив левую и правую части (1.77) на малый интервал времени, получим уравнение кинематической связи для скоростей тел:
. (1.78)
Дифференцируя полученное соотношение по времени, получаем искомую связь между ускорениями тел:
. (1.79)
Задача 1.8
(Кинематика простейших механических систем)
На вал радиуса R, закрепленный на оси, намотана веревка, на конце которой висит груз, опускающийся вниз (см. рис. 1.13). Закон движения груза: x = x0 + bt2, где x0 и b – постоянные положительные величины. Определить угловые скорость w и ускорение b произвольной точки обода вала, модуль ускорения a, его нормальную an и тангенциальную at проекции. Записать закон движения этой точки.
Решение
I. Нарисуем чертеж и изобразим на нем направление скорости движения груза. В соответствии с условием задачи направим ось X декартовой системы координат вертикально вниз (рис. 1.13). Для определения ускорения и закона движения произвольной точки A на ободе вала выберем полярную систему координат с полярной осью Y, в которой угол j однозначно определяет положение рассматриваемой точки A. Поскольку в условии задачи не оговаривается иное, веревку считаем нерастяжимой и что проскальзывания веревки относительно вала нет.
II. Запишем заданный в задаче закон движения груза в декартовой системе координат:
. (1.80)
Поскольку веревка нерастяжима, уравнение кинематической связи имеет вид:
. (1.81)
Для решения задачи записанные уравнения необходимо дополнить определениями (1.24) и выражениями (1.25) для интересующих нас величин, приведенными в п. 1.1.
III. Найдем законы изменения скорости груза и его ускорения в проекциях на оси декартовой системы координат, используя определения (1.6) и (1.12):
, ; (1.82)
, . (1.83)
Точки обода вала совершают неравномерное движение по окружности, причем модуль их скорости (поскольку нить нерастяжима и не проскальзывает по поверхности обода) в каждый момент времени равен модулю скорости груза, поэтому, используя (1.22) для угловой скорости w и углового ускорения b, получаем:
, (1.84)
. (1.85)
Поскольку проекция ускорения груза на ось X равна тангенциальной проекции ускорения точек обода, то:
. (1.86)
Нормальную проекцию ускорения определим, используя (1.22):
. (1.87)
Модуль полного ускорения произвольной точки A на ободе колеса найдем из соотношения (1.20):
. (1.88)
Закон движения произвольной точки A на ободе вала запишем в полярной системе координат:
, (1.89)
где j0 – начальное значение угловой координаты точки A в выбранной полярной системе координат.
Задача 1.9
(На кинематику материальной точки)
Закон движения движущейся в плоскости материальной точки, заданный в полярной системе координат, имеет следующий вид: r = r(t), φ = φ(t). Определить законы изменения проекций скорости и ускорения материальной точки на направления, задаваемые ортами декартовой и полярной систем координат, жестко связанных с телом отсчета. Начало декартовой системы координат совпадает с полюсом полярной системы, а ось X декартовой системы направлена вдоль полярной оси (см. рис. 1.14).
Решение
I. Выберем ось Y декартовой системы координат так, чтобы плоскость XY совпадала с плоскостью, в которой движется материальная точка M (рис. 1.14). Для решения задачи используем две системы координат – декартову систему координат XOY c ортами и , и полярную, орты которой и изображены на рис. 1.14. Заметим, что при движении материальной точки происходит изменение ориентации ортов полярной системы и , в то время как орты декартовой системы координат и не изменяют своего направления.
II, III. Закон движения материальной точки, заданный в полярной системе, запишем в декартовой системе координат XOY:
(1.90)
Дифференцируя закон движения (1.90) по времени, получаем искомые законы изменения проекций скорости материальной точки и ее ускорения в декартовой системе координат:
(1.91)
(1.92)
В формулах (1.92), (1.92) и далее для краткости опустим запись зависимости кинематических величин от времени.
Проекции скорости и ускорения материальной точки в полярной системе координат находим двумя способами.
1 способ. Скорость и ускорение материальной точки в полярной системе координат записываются в виде:
, (1.93)
. (1.94)
Следовательно, проекции скорости и ускорения материальной точки на направления, задаваемые ортами рассматриваемых систем координат, связаны соотношениями:
(1.95)
(1.96)
Сравнивая соотношения (1.90) и (1.95), а также (1.91) и (1.96), получим искомые проекции скорости и ускорения материальной точки в полярной системе координат:
(1.97)
(1.98)
2 способ. Запишем радиус-вектор материальной точки в полярной системе координат:
. (1.99)
Поскольку при движении материальной точки происходит изменение ориентации ортов полярной системы и , найдем скорость их изменения (см. рис. 1.15):
(1.100)
Теперь для нахождения скорости и ускорения точки в той же системе координат необходимо продифференцировать радиус-вектор (1.99) по времени с учетом (1.100):
, (1.101)
. (1.102)
В соответствии с (1.101) и (1.102) искомые проекции скорости и ускорения материальной точки в полярной системе координат равны:
(1.103)
(1.104)
Как видим, оба способа решения дают одинаковый результат.
Задача 1.10
(На кинематику материальной точки)
Движение материальной точки в полярной системе координат задается взаимосвязью полярных координат , при этом полярный угол возрастает линейно во времени . Определить зависимость модуля скорости и модуля ускорения материальной точки от времени.
Решение
I. Решаем задачу в заданной полярной системе координат. Заметим, что материальная точка M движется по замкнутой траектории, периодически, с периодом , возвращаясь в ту же точку пространства (см. рис. 1.16).
II. Определим закон изменения проекций скорости и ускорения материальной точки в полярной системе координат, воспользовавшись формулами (1.103) и (1.104), полученными в предыдущей задаче:
(1.105)
(1.106)
Тогда искомые модули скорости и ускорения материальной точки равны:
, (1.107)
(1.108)
Заметим, что материальная точка в моменты времени (где = 0, 1, 2, …) находится в начале (полюсе) полярной системы координат, имеет нулевую скорость, а ускорение, по модулю равное , направлено противоположно полярной оси.
Задача 1.11
(На кинематику материальной точки)
Планета движется вокруг Солнца в соответствии с законами Кеплера по эллиптической траектории . Параметр эллипса , эксцентриситет и секторную скорость считать заданными. Определить проекции ускорения планеты в зависимости от координат и полярной системы.
Решение
I. При решении задачи будем считать планету и Солнце материальными точками. Согласно первому закону Кеплера все планеты движутся по эллиптическим орбитам, причем Солнце находится в одном из фокусов эллипса O (см. рис. 1.17).
В соответствии с условием задачи введем полярную систему координат в плоскости движения планеты, полюс которой совпадает с Солнцем, а полярная ось совпадает с одной из осей эллипса.
Согласно второму закону Кеплера секторная скорость планеты, равная скорости изменения площади, описываемой радиус-вектором материальной точки, представляющим планету, постоянна при движении планеты вокруг Солнца.
II. Для нахождения проекций ускорения планеты в полярной системе координат воспользуемся формулами (1.104):
(1.109)
Поскольку в уравнения (1.109) входят производные полярных координат по времени, дополним эту систему уравнением траектории планеты и выражением для ее секторной скорости :
, (1.110)
. (1.111)
III. В соответствии с условием задачи секторная скорость постоянна при движении планеты по эллиптической траектории, поэтому ее производная по времени равна нулю:
. (1.112)
Сравнивая (1.112) с выражением (1.109) для проекции ускорения , видим, что . Следовательно, ускорение в любой момент времени имеет только проекцию , которая в соответствии с (1.109) является функцией производных полярных координат по времени.
Продифференцируем обе части уравнения траектории (1.110) по времени:
. (1.113)
Используя уравнение траектории (1.110) и выражение для секторной скорости (1.111), преобразуем (1.113) к виду:
. (1.114)
Продифференцируем теперь обе части уравнения (1.114) по времени
. (1.115)
Опять воспользуемся уравнением траектории (1.110) и выражением для секторной скорости (1.111) для исключения и из (1.115):
. (1.116)
В результате находим:
. (1.117)
Для нахождения искомой проекции ускорения планеты , как функции только координат полярной системы, подставим (1.116) и (см. (1.111)) в выражение (1.109):
. (1.118)
Таким образом, ускорение планеты, движущейся по эллиптической траектории, направлено к Солнцу, не зависит от полярного угла и обратно пропорционально квадрату расстояния до Солнца:
(1.119)
Задача 1.12
(На кинематику материальной точки)
Небольшое тело движется по гладкой внутренней поверхности полого вертикального цилиндра радиуса R. В начальный момент времени скорость тела направлена перпендикулярно оси цилиндра и равна . Определить законы изменения скорости и ускорения материальной точки в цилиндрической системе координат, а также угол между скоростью и ускорением.
Решение
I. Будем считать тело материальной точкой, которая движется по цилиндрической поверхности с постоянной вертикальной составляющей ускорения, равной ускорению свободного падения . Для решения задачи выберем цилиндрическую систему координат, ось Z которой совпадает с осью цилиндра, как показано на рис. 1.18. На том же рисунке изображены орты er, ej и ez цилиндрической системы. Ось, от которой отсчитывается угол системы координат, направим на положение тела в начальный момент времени.
II. В соответствии с условиями задачи и выбранной системой координат запишем начальные значения проекций скорости для рассматриваемого тела:
, , . (1.120)
Воспользуемся формулами (1.103) и (1.104) для проекций скорости и ускорения тела на направления, задаваемые ортами цилиндрической системы:
, , , (1.121)
, , . (1.122)
Кроме того, в соответствии с условиями задачи, запишем:
, , . (1.123)
III. Используя (1.121) – (1.123), получим законы изменения проекций скорости и ускорения:
, , ; (1.124)
, , . (1.125)
Таким образом, искомый закон изменения скорости и ускорения в цилиндрической системе координат имеет следующий вид:
, (1.126)
. (1.127)
Определим также искомый угол a между скоростью и ускорением тела:
. (1.128)
1.4. Задачи для самостоятельного решения
Задача 1
Из пушки, находящейся на самолете, летящем горизонтально со скоростью , выпущен снаряд в направлении движения самолета. Скорость снаряда относительно самолета равна . Пренебрегая сопротивлением воздуха, найти:
1) уравнение траектории снаряда относительно Земли ;
2) уравнение траектории снаряда относительно самолета ;
3) уравнение траектории самолета относительно снаряда .
Ответ: 1) , 2) ,
3) , . Оси X, X‘ и X» декартовой системы координат направлены горизонтально вдоль скорости самолета, а оси Y, Y‘ и Y» – вертикально вверх, при этом начало координат системы XY совпадает с положением самолета в момент выстрела пушки.
Задача 2
Лодка пересекает реку шириной d с постоянной относительно воды скоростью , перпендикулярной скорости течения реки, модуль которой нарастает от берегов к середине реки по линейному закону, меняясь от 0 до u. Найти траекторию лодки, а также снос лодки l вниз по течению от места ее отплытия до места причаливания на противоположном берегу реки.
Ответ: , при y < d/2; , при y > d/2; . Ось X декартовой системы координат XY направлена вдоль берега реки, а ось Y – поперек реки. Начало системы координат, жестко связанной с берегом реки, совпадает с местом отплытия лодки.
Задача 3
По движущемуся вниз эскалатору спускается пассажир со скоростью относительно эскалатора. Скорость эскалатора равна u. Спускаясь по неподвижному эскалатору пассажир проходит N ступеней. Сколько ступеней N‘ пройдет пассажир, спускаясь по движущемуся эскалатору?
Ответ: .
Задача 4
Два трактора, движущиеся со скоростями и , буксируют с помощью тросов автомобиль (см. рис.).
Определить модуль и направление скорости автомобиля в тот момент, когда тросы параллельны векторам и , а угол между ними равен a.
Ответ: ,
, где – угол между векторами и .
Задача 5
Тело А подвешено на нитях, перекинутых через блоки В и С малого диаметра так, что АВ = ВС (см. рис.).
Концы нитей тянут с одинаковыми скоростями . Расстояние между блоками В и С равно L. Найти модуль скорости тела А в тот момент, когда оно находится на расстоянии H от прямой ВС.
Ответ: .
Задача 6
Лодку подтягивают к пристани высотой Н с помощью веревки, наматываемой на вал лебедки. Радиус вала равен R << H. Вал вращается с постоянной угловой скоростью w. Определить зависимость модулей скорости и ускорения лодки от длины веревки L > Н. Движение лодки считается поступательным.
Ответ: , .
Задача 7.
Найти уравнение кинематической связи для ускорений тел, подвешенных на нерастяжимых нитях (см. рис.).
Ответ: , где , и – проекции ускорений тел на вертикальную ось декартовой системы координат.
Задача 8
Определить закон изменения модуля скорости материальной точки, движущейся в плоскости, если ее движение описывается в полярной системе координат следующим законом: , , где и – положительные постоянные величины.
Ответ: , при .
Задача 9
Четыре тела подвешены на нерастяжимых нитях (см. рис.). Найти ускорение тела 4, если известны ускорения остальных трех тел.
Ответ: , где , , и – проекции ускорений тел на вертикальную ось декартовой системы координат.
Задача 10
Найти уравнение кинематической связи для ускорений тел, подвешенных на нерастяжимых нитях так, как показано на рисунке.
Ответ: ,
где , , , и – проекции ускорений тел на вертикальную ось декартовой системы координат.
Задача 11
Два тела подвешены на нерастяжимых нитях, как показано на рисунке. Определить ускорение тела 2, если известно ускорение тела 1.
Ответ: , где и – проекции ускорений тел на вертикальную ось декартовой системы координат.
[1] Далее в тексте, если это не оговаривается особо, используется декартова система координат.
§ 1.2. Уравнение движения груза, подвешенного на пружине
Согласно второму закону Ньютона произведение массы тела m на ускорение 
m 
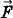
Второй закон Ньютона (1.2.1) непосредственно описывает движение тела, размеры которого не оказывают существенного влияния на характер движения. В таком случае тело можно считать материальной точкой.
Чтобы записать второй закон Ньютона для проекций на оси координат, надо выбрать подходящую систему отсчета, относительно которой уравнение движения выглядит особенно просто и потому удобно для решения. Далее надо выяснить, как модули и направления сил зависят от положения (координат) тела и его скорости. Если тело движется вдоль прямой, как в случае колебаний груза на пружине, то сделать это нетрудно.
Запишем уравнение движения для груза на пружине. На груз действует сила упругости 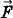
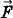

Начало отсчета (точку О) выберем на уровне положения равновесия. В положении равновесия пружина растянута на величину x0, значение которой определяется из закона Гука: kx0 = mg, где k — жесткость пружины, m — масса груза, a g — ускорение свободного падения. Отсюда

Проекция силы упругости
где x — координата груза относительно положения равновесия. Величина x0 + х представляет собой удлинение пружины (см. рис. 1.7).
Уравнение движения груза запишется так:
Подставляя в это уравнение значение x0 из выражения (1.2.2), получим окончательно:
Уравнение движения не содержит силы тяжести. Сила тяжести, действуя на груз, вызывает растяжение пружины на постоянную величину. Но это не влияет на характер движения груза. Просто колебания происходят относительно положения равновесия тела при растянутой на x0 пружине. В отсутствие тяготения уравнение движения (1.2.4) имело бы точно такую же форму, но только колебания происходили бы относительно конца нерастянутой пружины. Наличие силы тяжести несущественно для колебаний груза на пружине в отличие от колебаний маятника.
Масса m и жесткость пружины k — постоянные величины. Разделив левую и правую части уравнения (1.2.4) на m и введя новое обозначение
Это уравнение колебаний груза на пружине. Оно очень простое: ускорение груза прямо пропорционально его координате X, взятой с противоположным знаком. Самым замечательным является то, что такие же (с точностью до обозначений) уравнения описывают свободные колебания самых различных систем, в частности колебания математического маятника.
Постоянная ω0 имеет важный физический смысл. Как мы впоследствии увидим, — это циклическая частота колебаний груза. Она выражается в секундах в минус первой степени.
Колебания груза на пружине — формулы, уравнения и задачи
Общие сведения
Колебания — это изменения какой-либо величины в точности или приблизительно повторяющиеся во времени. Если рассматривать процесс, с точки зрения механики, то он описывается положением тела. Повторение в точности является периодическим. Математически это можно записать формулой: x (t + T) = x (t), где T — время, в течение которого совершается одно полное колебание (период). Число циклов принято обозначать буквой N. Его находят как отношение времени к периоду: N = t / T.
При исследовании процесса не всегда бывает удобно оперировать временем, поэтому часто используют число колебаний за единицу времени. Эта величина называется частотой. Находят её количество по формуле: f = 1 / T. Доказать справедливость приведённого равенства просто. Число колебаний зависит от времени и частоты: N = f * t. Отсюда: f = N / t = (t / T) / t = 1 / T.
Очень важно не только понимать суть характеристик колебания, но и знать единицы его измерения. Вот основные из них:
- период — секунды (с);
- частота — герцы (Гц);
- число колебаний — безразмерная величина.
Если в течение времени меняется и координата, то периодически будет изменяться и скорость. Значит: vx (t + T) = Vx (t).
Исходя из верности равенства, можно сказать, что условие периодичности будет справедливо и для проекции, то есть изменения ускорения. Отсюда следует, что сила действующая на тело тоже будет переменной: Fx (t + T) = Fx (t).
При процессе также происходит изменение потенциальной и кинетической энергий. Действительно, так как в процессе колебания скорость не является постоянной величиной, то соответственно будет меняться кинетическая работа. Потенциальная же энергия зависит от координат. Например, если рассмотреть период колебаний пружинного маятника, то за это время тело переместится из нижнего положения в верхнее и вернётся обратно. Значит, координата физического объекта изменится от нуля до какого-то граничного значения.
Следует отметить, что периодичные движения обязательно будут происходить в той системе, в которой есть положение равновесия. Причём оно должно быть устойчивым. То есть существует равнодействующая сила, стремящаяся привести объект в положение, соответствующее покою. Поэтому для поддержания отклонений нужна дополнительная сила. Колебательную систему (осциллятор) под действием вынужденной периодической силы называют вынужденной.
Пружинный маятник
Это устройство является простейшим примером свободных колебаний. В его состав входит кронштейн, пружина и груз. В качестве последнего может выступать любое физическое тело. Масса пружины по сравнению с грузом считается малой и при исследованиях не учитывается.
При изучении такой системы важной задачей является измерение периода движения тела, подвешенного к пружине. Определение понятию пружинного маятника, которое даётся в учебниках по физике довольно обобщённое. Считается, что это конструкция, в которой тело, имеющее массу m, подвешено на упругой пружине обладающей жёсткостью K. При этом из состояния равновесия систему может вывести упругая сила F = — k * x, где: x- расстояние от середины пружинного элемента до поверхности прикреплённого к нему груза.
Можно выделить два достаточных условия возникновения свободных колебаний:
- Во время отклонения тела от положения равновесия должна возникать возвращающая сила.
- Силы сопротивления (трения) должны быть малы по сравнению со стремящей вернуть энергией тело назад.
Суть изучения гармонических колебаний состоит в определении их частоты движения или периода. В пружинном маятнике, впрочем, как и в любой колебательной системе, параметры зависят от ряда характеристик. Из основных величин, описывающих процесс, можно выделить: массу груза и жёсткость. Поэтому задача и состоит в выяснении, как период зависит от этих двух параметров.
Во время экспериментов регулировать массу довольно легко. Для этого можно взять эталонные гири и, соединяя их, увеличивать вес. Жёсткость же пружины можно изменить, добавляя параллельно или последовательно к ней другое сжимающееся тело. Чтобы выяснить, как будет изменяться характеристика растягивающегося элемента, нужно знать, что же представляет собой параметр. Так, под жёсткостью тела понимают отношение силы упругости к удлинению: k0 = F / Δ L. Измеряется величина в ньютонах, делённых на метр (Н/м).
Исходя из правила, если соединить две пружины параллельно и деформировать их, то можно утверждать, что первый и второй элемент растянется на одинаковую длину ΔL. Значит, возникнет две одинаково направленных силы упругости. Отсюда равнодействующая будет равняться: K = 2F/ ΔL = 2k0. Для последовательного же соединения длина всей системы увеличится на 2 ΔL. Сила упругости будет равна F. Соответственно, жёсткость будет изменяться по формуле: K = F / 2ΔL = k0 / 2.
Зависимость периода
При проведении эксперимента можно исследовать пять различных комбинаций поведения груза на пружине — два варианта связаны с весом и три с жёсткостью. Чтобы выполнить опыт самостоятельно нужно будет взять вертикальный кронштейн, две одинаковые пружины и два равных по весу груза. Так как в реальности период будет довольно маленький, то для его измерения можно взять время, например, пятидесяти колебаний, а потом полученный результат разделить на это число. Подсчёт времени удобно выполнять с помощью секундомера.
Вычисленные результаты нужно занести в таблицу. Примерный порядок чисел должен получиться таким:
| k m | m0 | 2m0 |
| k0 / 2 | 0,68 | 0,93 |
| k0 | 0,46 | 0,64 |
| 2k0 | 0.34 | 0,47 |
Эти данные можно проанализировать. Выводы будут следующими:
- с ростом массы физического тела период цикличности увеличивается;
- по мере увеличения жёсткости период колебаний уменьшается.
Приведённые утверждения, возможно, описать и количественно. Исходя из результатов, величины, стоящие в ячейке m0k0 и 2m02ko почти совпадают. С точки зрения физики, так и должно быть. Если взять грузик на пружине и измерить характеристику, а потом добавить к нему точно такую же систему, то период не поменяется. Это и можно наблюдать во время опыта. Значит, период движения зависит от того каким будет отношение массы к жёсткости.
По аналогии можно рассмотреть, как влияет жёсткость. Из эксперимента, видно, что если её увеличить дважды на одну и ту же величину, то она возрастёт в четыре раза, а значение обратное частоте уменьшится на это же число. Отсюда можно предположить, что период будет обратно пропорционален корню квадратному из жёсткости.
Объединив эти две гипотезы можно сделать заключение. Что период амплитуды колебаний груза на пружине будет прямо пропорционален корню квадратного из отношения массы к жёсткости: T = √(m / k). Проверить это утверждение можно по теории размерности. Подставив в формулу единицы измерения, получим: √(m / k) = √(кг / (Н/м)) = √(кг * м / Н). Учитывая, что ньютон — это отношение метра к секунде в квадрате или килограмму, умноженному на метр и делённому на секунду, размерное равенство примет вид: √(кг * м/Н) = √(c 2 * м/м) = √с 2 = с.
Для написания полной формулы в равенство нужно вести ещё коэффициент. Он будет равняться 2p. Значит, период колебаний пружинного маятника количественно описывается выражением: T = 2p * √ (m / k).
Примеры решения задач
Практические задания помогают лучше разобраться в теоретическом материале и запомнить нужные для решения формулы. Существуют различные примеры, с помощью которых можно довольно быстро проработать весь изученный курс. Вот два задания с подробным описанием решения на вычисления параметров пружинных колебаний тела. Разобравшись в них, можно переходить к самостоятельному вычислению более сложных примеров.
Задание № 1. Груз, подвешенный к пружине, перемещается циклически по вертикальной оси. За восемь секунд он совершил тридцать два колебания. Определить частоту. Итак, по условию задания дано время t = 8 c и число полного перемещения тела N = 32. Чтобы решить эту задачу нужно воспользоваться формулой нахождения периода: T = t / N. Все величины для этого есть: T = 8 c / 32 = 1 / 4 = 0,25 секунды. Частота связана с периодом выражением: f = 1 / T. После подстановки чисел получится ответ равный четырём герцам.
Задание № 2. Грузик совершает колебания на пружине с жёсткостью сто ньютон на метр. При этом максимальная скорость движения составляет два метра в секунду. Вычислить массу тела учитывая, что максимальная амплитуда отклонения от точки покоя составляет десять сантиметров. Силой трения пренебречь.
При решении примера нужно рассуждать следующим образом. Когда будет максимальное растяжение пружины, то скорость груза равна нулю: V1 = 0. Значит, кинетическая энергия тоже будет нулевой: Ek1 = 0.
В этот момент останется только потенциальная энергия вытянутой пружины Ep1. В положении равновесия скорость тела максимальная и равняется V = 2 м/с. Так как пружина в этот момент нерастянута и несжатая, то Ep = 0.
По закону сохранения энергии: Ek1 + Ep1 = Ek + Ep. Кинетическая работа при растянутой пружине равняется нулю, так же как и потенциальная в состоянии покоя, значит, Ep1 = (k * L 2 ) / 2, где L — удлинение, а k — жёсткость. Энергию же можно найти так: Ek = mV 2 / 2. Так как тело совершает колебания около положения равновесия, то вытянутость пружины будет равняться амплитуде.
Перед тем как непосредственно переходить к составлению итоговой формулы и вычислениям необходимо все значения измерений привести в соответствии с СИ. Так, амплитуда указана в сантиметрах, поэтому её нужно перевести в метры. Теперь можно переходить к составлению отношения и подстановки данных: (k * L 2 ) / 2 = mV 2 / 2. Отсюда: m = (k * L) / V 2 = (100 Н/м * 0,1 2 м) / 2 2 м/с = 1 / 4 = 0,25 килограмма.
Динамические уравнения и законы движения груза на пружине
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.
Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению (см. §2.1):
В этом соотношении – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:
Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .
Таким образом, груз некоторой массы , прикрепленный к пружине жесткости , второй конец которой закреплен неподвижно (рис. 2.2.1), составляют систему, способную в отсутствие трения совершать свободные гармонические колебания. Груз на пружине называют линейным гармоническим осциллятором .
 |
||
| Рисунок 2.2.1.
Круговая частота свободных колебаний груза на пружине находится из второго закона Ньютона: откуда Частота называется собственной частотой колебательной системы. Период гармонических колебаний груза на пружине равен При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину , равную и колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты и периода колебаний справедливы и в этом случае. Строгое описание поведения колебательной системы может быть дано, если принять во внимание математическую связь между ускорением тела и координатой : ускорение является второй производной координаты тела по времени : Поэтому второй закон Ньютона для груза на пружине может быть записан в виде или
где Все физические системы (не только механические), описываемые уравнением (*), способны совершать свободные гармонические колебания, так как решением этого уравнения являются гармонические функции вида Уравнение (*) называется уравнением свободных колебаний . Следует обратить внимание на то, что физические свойства колебательной системы определяют только собственную частоту колебаний или период . Такие параметры колебательного процесса, как амплитуда m и начальная фаза , определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени. Если, например, груз был смещен из положения равновесия на расстояние и затем в момент времени отпущен без начальной скорости, то m = , . Если же грузу, находившемуся в положении равновесия, с помощью резкого толчка была сообщена начальная скорость Таким образом, амплитуда m свободных колебаний и его начальная фаза определяются начальными условиями . Существует много разновидностей механических колебательных систем, в которых используются силы упругих деформаций. На рис. 2.2.2 показан угловой аналог линейного гармонического осциллятора, совершающий крутильные колебания. Горизонтально расположенный диск висит на упругой нити, закрепленной в его центре масс. При повороте диска на угол возникает момент сил упругой деформации кручения: Это соотношение выражает закон Гука для деформации кручения. Величина аналогична жесткости пружины . Второй закон Ньютона для вращательного движения диска записывается в виде (см. §1.23) где – момент инерции диска относительно оси, проходящий через центр масс, – угловое ускорение. По аналогии с грузом на пружине можно получить: Крутильный маятник широко используется в механических часах. Его называют балансиром. В балансире момент упругих сил создается с помощью спиралевидной пружинки. источники: http://nauka.club/fizika/kolebaniya-gruza-na-pruzhine.html http://physics.ru/courses/op25part1/content/chapter2/section/paragraph2/theory.html |
Вообще, эта задача не из учебника по физике, а из учебника по математике. Я не думаю, что здесь делали упор на физические законы и явления. Скорей всего, здесь просто нужно было составить дифференциальное уравнение и решить его.
Если это задача из задачника по математике, то должно быть четкое, недвусмысленное указание в условиях, что колебания свободные. ИМХО. Ибо, с точки зрения математики Вы имеете диффур с хрен знает какой правой частью. Что-то должно указывать на то, что при 


— 26.12.2017, 22:33 —
А если таких указаний нет в задачнике по математике, то, ИМХО, Вы не имеете никаких прав исключать другие решения, математически
возможные. Впрочем, в этом случае, и физически возможные.
— 26.12.2017, 22:42 —
Боюсь, что это слишком хитро.
(про детей, розетку и провода)
недавно в курилке возник вопрос: «как объяснить ребенку 4-х лет, откуда берется электричество в розетке».
на попытки объяснить, что «из проводов», вспоминая некоторые темы тут…
сказал, что «электричество» передается не по проводам, а полем вокруг проводов. За что был заплеван жвачками.
Но возразил: «с малых лет надо прививать правильный взгляд на окружающий мир»






































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































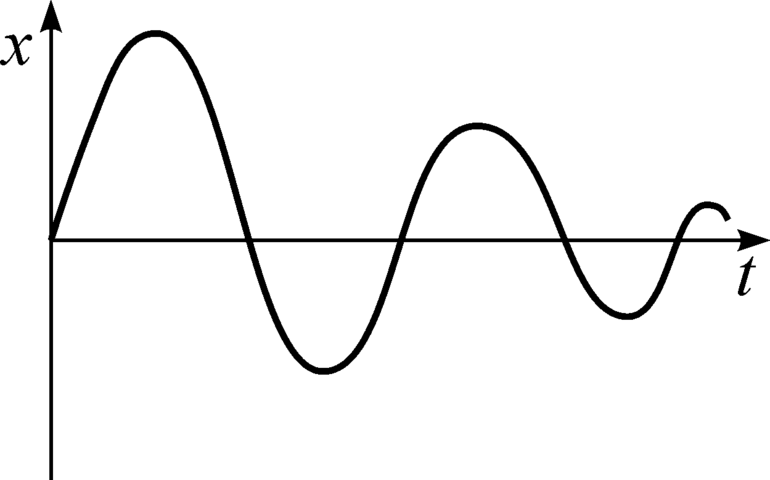


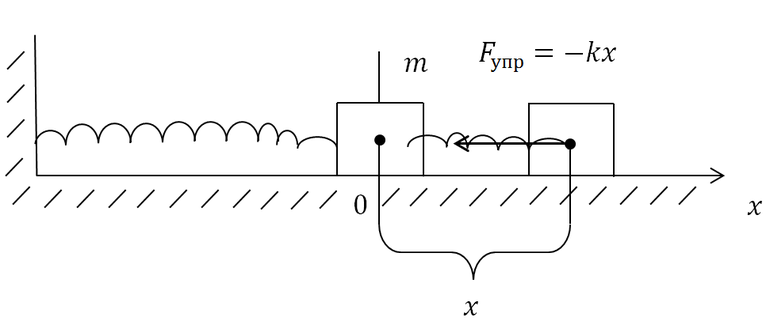
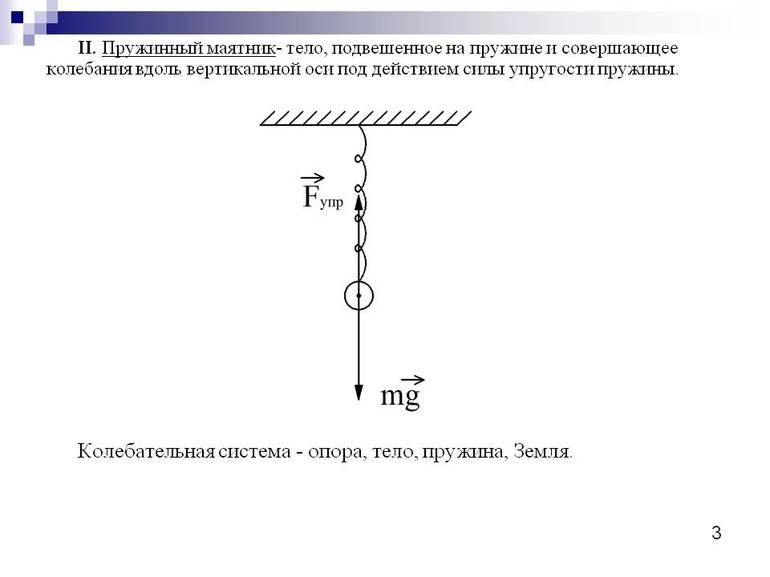
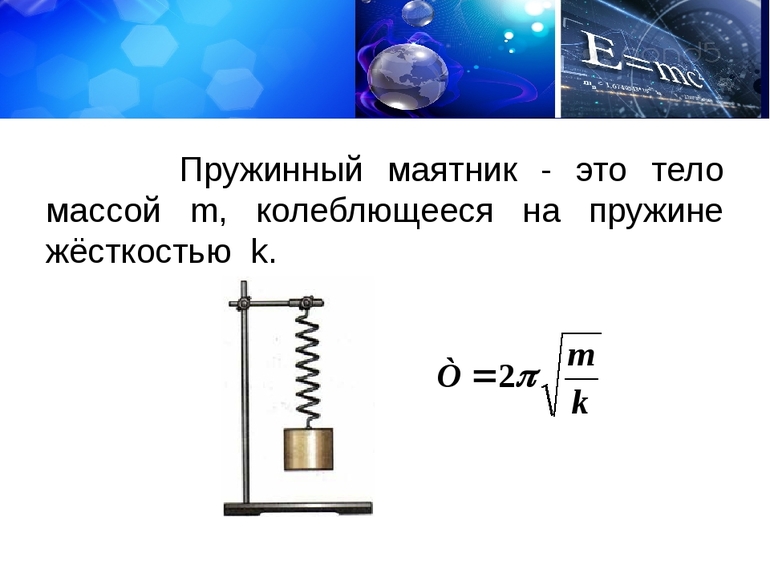
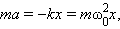
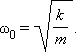
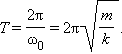
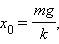
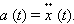
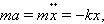
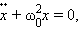
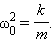
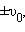 то
то