Закон стефана больцмана как найти температуру - Исправление недочетов и поиск решений вместе с Examum.ru

Graph of a function of total emitted energy of a black body $j^{star}$ proportional to its thermodynamic temperature . In blue is a total energy according to the Wien approximation, $j^{star}_{W} = j^{star} / zeta(4) approx 0.924 , sigma T^{4} !,$

The Stefan–Boltzmann law describes the power radiated from a black body in terms of its temperature. Specifically, the Stefan–Boltzmann law states that the total energy radiated per unit surface area of a black body across all wavelengths per unit time $j^{star}$ (also known as the black-body radiant emittance) is directly proportional to the fourth power of the black body’s thermodynamic temperature T:

$j^{star} = sigma T^{4}.$

The constant of proportionality σ, called the Stefan–Boltzmann constant, is derived from other known physical constants. Since 2019, the value of the constant is

${displaystyle sigma ={frac {2pi ^{5}k^{4}}{15c^{2}h^{3}}}=5.670 374 419...times 10^{-8},mathrm {W,m^{-2},K^{-4}} ,}$

where k is the Boltzmann constant, h is the Planck constant, and c is the speed of light in vacuum. The radiance from a specified angle of view (watts per square metre per steradian) is given by

$L = frac{j^{star}}pi = fracsigmapi T^{4}.$

A body that does not absorb all incident radiation (sometimes known as a grey body) emits less total energy than a black body and is characterized by an emissivity, :

$j^{star} = varepsilonsigma T^{4}.$

The radiant emittance $j^{star}$ has dimensions of energy flux (energy per unit time per unit area), and the SI units of measure are joules per second per square metre, or equivalently, watts per square metre. The SI unit for absolute temperature T is the kelvin. is the emissivity of the grey body; if it is a perfect blackbody, . In the still more general (and realistic) case, the emissivity depends on the wavelength, .

To find the total power radiated from an object, multiply by its surface area, :

$P= A j^{star} = A varepsilonsigma T^{4}.$

Wavelength- and subwavelength-scale particles,^[1] metamaterials,^[2] and other nanostructures are not subject to ray-optical limits and may be designed to exceed the Stefan–Boltzmann law.

History[edit]

In 1864, John Tyndall presented measurements of the infrared emission by a platinum filament and the corresponding color of the filament.^[3]
The proportionality to the fourth power of the absolute temperature was deduced by Josef Stefan (1835–1893) in 1877 on the basis of Tyndall’s experimental measurements, in the article Über die Beziehung zwischen der Wärmestrahlung und der Temperatur (On the relationship between thermal radiation and temperature) in the Bulletins from the sessions of the Vienna Academy of Sciences.^[4]^[5]

A derivation of the law from theoretical considerations was presented by Ludwig Boltzmann (1844–1906) in 1884, drawing upon the work of Adolfo Bartoli.^[6]
Bartoli in 1876 had derived the existence of radiation pressure from the principles of thermodynamics. Following Bartoli, Boltzmann considered an ideal heat engine using electromagnetic radiation instead of an ideal gas as working matter.

The law was almost immediately experimentally verified. Heinrich Weber in 1888 pointed out deviations at higher temperatures, but perfect accuracy within measurement uncertainties was confirmed up to temperatures of 1535 K by 1897.^[7]
The law, including the theoretical prediction of the Stefan–Boltzmann constant as a function of the speed of light, the Boltzmann constant and the Planck constant, is a direct consequence of Planck’s law as formulated in 1900.

As of the 2019 redefinition of SI base units, which fixes the values of the Boltzmann constant k, the Planck constant h, and the speed of light c, the Stefan–Boltzmann constant is exactly

${displaystyle sigma ={frac {2pi ^{5}k^{4}}{15c^{2}h^{3}}}={frac {2pi ^{5}left(1.380 649times 10^{-23}right)^{4}}{15left(2.997 924 58times 10^{8}right)^{2}left(6.626 070 15times 10^{-34}right)^{3}}}mathrm {frac {W}{m^{2}cdot K^{4}}} }$

σ = 5.670374419…×10⁻⁸ W/(m²K⁴).^[8]

Prior to this, the value of sigma was calculated from the measured value of the gas constant.^[9]

The numerical value of the Stefan–Boltzmann constant is different in other systems of units. For example, in thermochemistry it is often expressed in cal⋅cm⁻²⋅day⁻¹⋅K⁻⁴:

σ = 1.170937…×10⁻⁷ cal cm⁻²⋅day⁻¹⋅K⁻⁴.

Likewise, in US customary units the Stefan–Boltzmann constant is^[10]

σ = 1.713441…×10⁻⁹ BTU⋅hr⁻¹⋅ft⁻²⋅°R⁻⁴.

Examples[edit]

Temperature of the Sun[edit]

With his law, Stefan also determined the temperature of the Sun’s surface.^[11] He inferred from the data of Jacques-Louis Soret (1827–1890)^[12] that the energy flux density from the Sun is 29 times greater than the energy flux density of a certain warmed metal lamella (a thin plate). A round lamella was placed at such a distance from the measuring device that it would be seen at the same angular diameter as the Sun. Soret estimated the temperature of the lamella to be approximately 1900 °C to 2000 °C. Stefan surmised that ⅓ of the energy flux from the Sun is absorbed by the Earth’s atmosphere, so he took for the correct Sun’s energy flux a value 3/2 times greater than Soret’s value, namely 29 × 3/2 = 43.5.

Precise measurements of atmospheric absorption were not made until 1888 and 1904. The temperature Stefan obtained was a median value of previous ones, 1950 °C and the absolute thermodynamic one 2200 K. As 2.57⁴ = 43.5, it follows from the law that the temperature of the Sun is 2.57 times greater than the temperature of the lamella, so Stefan got a value of 5430 °C or 5700 K. This was the first sensible value for the temperature of the Sun. Before this, values ranging from as low as 1800 °C to as high as 13,000,000 °C^[13] were claimed. The lower value of 1800 °C was determined by Claude Pouillet (1790–1868) in 1838 using the Dulong–Petit law.^[14] Pouillet also took just half the value of the Sun’s correct energy flux.

Temperature of stars[edit]

The temperature of stars other than the Sun can be approximated using a similar means by treating the emitted energy as a black body radiation.^[15] So:

${displaystyle L=4pi R^{2}sigma T^{4}}$

where L is the luminosity, σ is the Stefan–Boltzmann constant, R is the stellar radius and T is the effective temperature. This formula can then be rearranged to calculate the temperature:

${displaystyle T={sqrt[{4}]{frac {L}{4pi R^{2}sigma }}}}$

or alternatively the radius:

${displaystyle R={sqrt {frac {L}{4pi sigma T^{4}}}}}$

The same formulae can also be simplified to compute the parameters relative to the Sun:

${displaystyle {frac {L}{L_{odot }}}=left({frac {R}{R_{odot }}}right)^{2}left({frac {T}{T_{odot }}}right)^{4}}$

${displaystyle {frac {T}{T_{odot }}}=left({frac {L}{L_{odot }}}right)^{1/4}{sqrt {frac {R_{odot }}{R}}}}$

${displaystyle {frac {R}{R_{odot }}}=left({frac {T_{odot }}{T}}right)^{2}{sqrt {frac {L}{L_{odot }}}}}$

where R_odot is the solar radius, and so forth. They can also be rewritten in terms of the surface area A and radiant emittance $j^{star}$ :

${displaystyle L=Aj^{star }}$

${displaystyle j^{star }={frac {L}{A}}}$

${displaystyle A={frac {L}{j^{star }}}}$

where ${displaystyle A=4pi R^{2}}$ and ${displaystyle j^{star }=sigma T^{4}.}$

With the Stefan–Boltzmann law, astronomers can easily infer the radii of stars. The law is also met in the thermodynamics of black holes in so-called Hawking radiation.

Effective temperature of the Earth[edit]

Similarly we can calculate the effective temperature of the Earth T_⊕ by equating the energy received from the Sun and the energy radiated by the Earth, under the black-body approximation (Earth’s own production of energy being small enough to be negligible). The luminosity of the Sun, L_⊙, is given by:

${displaystyle L_{odot }=4pi R_{odot }^{2}sigma T_{odot }^{4}}$

At Earth, this energy is passing through a sphere with a radius of a₀, the distance between the Earth and the Sun, and the irradiance (received power per unit area) is given by

${displaystyle E_{oplus }={frac {L_{odot }}{4pi a_{0}^{2}}}}$

The Earth has a radius of R_⊕, and therefore has a cross-section of ${displaystyle pi R_{oplus }^{2}}$ . The radiant flux (i.e. solar power) absorbed by the Earth is thus given by:

${displaystyle Phi _{text{abs}}=pi R_{oplus }^{2}times E_{oplus }:}$

Because the Stefan–Boltzmann law uses a fourth power, it has a stabilizing effect on the exchange and the flux emitted by Earth tends to be equal to the flux absorbed, close to the steady state where:

${displaystyle {begin{aligned}4pi R_{oplus }^{2}sigma T_{oplus }^{4}&=pi R_{oplus }^{2}times E_{oplus }\&=pi R_{oplus }^{2}times {frac {4pi R_{odot }^{2}sigma T_{odot }^{4}}{4pi a_{0}^{2}}}\end{aligned}}}$

T_⊕ can then be found:

${displaystyle {begin{aligned}T_{oplus }^{4}&={frac {R_{odot }^{2}T_{odot }^{4}}{4a_{0}^{2}}}\T_{oplus }&=T_{odot }times {sqrt {frac {R_{odot }}{2a_{0}}}}\&=5780;{rm {K}}times {sqrt {6.957times 10^{8};{rm {m}} over 2times 1.495 978 707times 10^{11};{rm {m}}}}\&approx 279;{rm {K}}end{aligned}}}$

where T_⊙ is the temperature of the Sun, R_⊙ the radius of the Sun, and a₀ is the distance between the Earth and the Sun. This gives an effective temperature of 6 °C on the surface of the Earth, assuming that it perfectly absorbs all emission falling on it and has no atmosphere.

The Earth has an albedo of 0.3, meaning that 30% of the solar radiation that hits the planet gets scattered back into space without absorption. The effect of albedo on temperature can be approximated by assuming that the energy absorbed is multiplied by 0.7, but that the planet still radiates as a black body (the latter by definition of effective temperature, which is what we are calculating). This approximation reduces the temperature by a factor of 0.7^1/4, giving 255 K (−18 °C).^[16]^[17]

The above temperature is Earth’s as seen from space, not ground temperature but an average over all emitting bodies of Earth from surface to high altitude. Because of the greenhouse effect, the Earth’s actual average surface temperature is about 288 K (15 °C), which is higher than the 255 K effective temperature, and even higher than the 279 K temperature that a black body would have.

In the above discussion, we have assumed that the whole surface of the earth is at one temperature. Another interesting question is to ask what the temperature of a blackbody surface on the earth would be assuming that it reaches equilibrium with the sunlight falling on it. This of course depends on the angle of the sun on the surface and on how much air the sunlight has gone through. When the sun is at the zenith and the surface is horizontal, the irradiance can be as high as 1120 W/m².^[18] The Stefan–Boltzmann law then gives a temperature of

${displaystyle T=left({frac {1120{text{ W/m}}^{2}}{sigma }}right)^{1/4}approx 375{text{ K}}}$

or 102 °C. (Above the atmosphere, the result is even higher: 394 K.) We can think of the earth’s surface as «trying» to reach equilibrium temperature during the day, but being cooled by the atmosphere, and «trying» to reach equilibrium with starlight and possibly moonlight at night, but being warmed by the atmosphere.

Origination[edit]

Thermodynamic derivation of the energy density[edit]

The fact that the energy density of the box containing radiation is proportional to $T^{4}$ can be derived using thermodynamics.^[19]^[20] This derivation uses the relation between the radiation pressure p and the internal energy density , a relation that can be shown using the form of the electromagnetic stress–energy tensor. This relation is:

${displaystyle p={frac {u}{3}}.}$

Now, from the fundamental thermodynamic relation

we obtain the following expression, after dividing by and fixing :

${displaystyle left({frac {partial U}{partial V}}right)_{T}=Tleft({frac {partial S}{partial V}}right)_{T}-p=Tleft({frac {partial p}{partial T}}right)_{V}-p.}$

The last equality comes from the following Maxwell relation:

${displaystyle left({frac {partial S}{partial V}}right)_{T}=left({frac {partial p}{partial T}}right)_{V}.}$

From the definition of energy density it follows that

where the energy density of radiation only depends on the temperature, therefore

${displaystyle left({frac {partial U}{partial V}}right)_{T}=uleft({frac {partial V}{partial V}}right)_{T}=u.}$

Now, the equality

${displaystyle left({frac {partial U}{partial V}}right)_{T}=Tleft({frac {partial p}{partial T}}right)_{V}-p,}$

after substitution of ${displaystyle left({frac {partial U}{partial V}}right)_{T}.}$ Meanwhile, the pressure is the rate of momentum change per unit area. Since the momentum of a photon is the same as the energy divided by the speed of light,

${displaystyle u={frac {T}{3}}left({frac {partial u}{partial T}}right)_{V}-{frac {u}{3}},}$

where the 1/3 factor comes from the projection of the momentum transfer onto the normal to the wall of the container.

Since the partial derivative ${displaystyle left({frac {partial u}{partial T}}right)_{V}}$ can be expressed as a relationship between only and (if one isolates it on one side of the equality), the partial derivative can be replaced by the ordinary derivative. After separating the differentials the equality becomes

${displaystyle {frac {du}{4u}}={frac {dT}{T}},}$

which leads immediately to , with as some constant of integration.

Derivation from Planck’s law[edit]

The law can be derived by considering a small flat black body surface radiating out into a half-sphere. This derivation uses spherical coordinates, with θ as the zenith angle and φ as the azimuthal angle; and the small flat blackbody surface lies on the xy-plane, where θ = ^π/₂.

The intensity of the light emitted from the blackbody surface is given by Planck’s law,

${displaystyle I(nu ,T)={frac {2hnu ^{3}}{c^{2}}}{frac {1}{e^{hnu /(kT)}-1}},}$

where

The quantity is the power radiated by a surface of area A through a solid angle dΩ in the frequency range between ν and ν + dν.

The Stefan–Boltzmann law gives the power emitted per unit area of the emitting body,

${displaystyle {frac {P}{A}}=int _{0}^{infty }I(nu ,T),dnu int cos theta ,dOmega }$

Note that the cosine appears because black bodies are Lambertian (i.e. they obey Lambert’s cosine law), meaning that the intensity observed along the sphere will be the actual intensity times the cosine of the zenith angle.
To derive the Stefan–Boltzmann law, we must integrate over the half-sphere and integrate from 0 to ∞.

${displaystyle {begin{aligned}{frac {P}{A}}&=int _{0}^{infty }I(nu ,T),dnu int _{0}^{2pi },dvarphi int _{0}^{pi /2}cos theta sin theta ,dtheta \&=pi int _{0}^{infty }I(nu ,T),dnu end{aligned}}}$

Then we plug in for I:

${displaystyle {frac {P}{A}}={frac {2pi h}{c^{2}}}int _{0}^{infty }{frac {nu ^{3}}{e^{frac {hnu }{kT}}-1}},dnu }$

To evaluate this integral, do a substitution,

${displaystyle {begin{aligned}u&={frac {hnu }{kT}}\[6pt]du&={frac {h}{kT}},dnu end{aligned}}}$

which gives:

${displaystyle {frac {P}{A}}={frac {2pi h}{c^{2}}}left({frac {kT}{h}}right)^{4}int _{0}^{infty }{frac {u^{3}}{e^{u}-1}},du.}$

The integral on the right is standard and goes by many names: it is a particular case of a Bose–Einstein integral, the polylogarithm, or the Riemann zeta function . The value of the integral is ${displaystyle Gamma (4)zeta (4)={frac {pi ^{4}}{15}}}$ (where is the Gamma function), giving the result that, for a perfect blackbody surface:

${displaystyle j^{star }=sigma T^{4}~,~~sigma ={frac {2pi ^{5}k^{4}}{15c^{2}h^{3}}}={frac {pi ^{2}k^{4}}{60hbar ^{3}c^{2}}}.}$

Finally, this proof started out only considering a small flat surface. However, any differentiable surface can be approximated by a collection of small flat surfaces. So long as the geometry of the surface does not cause the blackbody to reabsorb its own radiation, the total energy radiated is just the sum of the energies radiated by each surface; and the total surface area is just the sum of the areas of each surface—so this law holds for all convex blackbodies, too, so long as the surface has the same temperature throughout. The law extends to radiation from non-convex bodies by using the fact that the convex hull of a black body radiates as though it were itself a black body.

Energy density[edit]

The total energy density U can be similarly calculated, except the integration is over the whole sphere and there is no cosine, and the energy flux (U c) should be divided by the velocity c to give the energy density U:

${displaystyle U={frac {1}{c}}int _{0}^{infty }I(nu ,T),dnu int ,dOmega }$

Thus ${textstyle int _{0}^{pi /2}cos theta sin theta ,dtheta }$ is replaced by ${textstyle int _{0}^{pi }sin theta ,dtheta }$ , giving an extra factor of 4.

Thus, in total:

${displaystyle U={frac {4}{c}},sigma ,T^{4}}$

The product ${displaystyle {frac {4}{c}}sigma }$ is sometimes known as the radiation constant or radiation density constant.^[21]^[22]

Notes[edit]

^
Bohren, Craig F.; Huffman, Donald R. (1998). Absorption and scattering of light by small particles. Wiley. pp. 123–126. ISBN 978-0-471-29340-8.
^
Narimanov, Evgenii E.; Smolyaninov, Igor I. (2012). «Beyond Stefan–Boltzmann Law: Thermal Hyper-Conductivity». Conference on Lasers and Electro-Optics 2012. OSA Technical Digest. Optical Society of America. pp. QM2E.1. CiteSeerX 10.1.1.764.846. doi:10.1364/QELS.2012.QM2E.1. ISBN 978-1-55752-943-5. S2CID 36550833.
^
- Tyndall, John (1864). «On luminous [i.e., visible] and obscure [i.e., infrared] radiation». Philosophical Magazine. 4th series. 28: 329–341. ; see p. 333.
In his physics textbook of 1875, Adolph Wüllner quoted Tyndall’s results and then added estimates of the temperature that corresponded to the platinum filament’s color:
- Wüllner, Adolph (1875). Lehrbuch der Experimentalphysik [Textbook of experimental physics] (in German). Vol. 3. Leipzig, Germany: B.G. Teubner. p. 215.
From (Wüllner, 1875), p. 215: «Wie aus gleich zu besprechenden Versuchen von Draper hervorgeht, … also fast um das 12fache zu.» (As follows from the experiments of Draper, which will be discussed shortly, a temperature of about 525°[C] corresponds to the weak red glow; a [temperature] of about 1200°[C], to the full white glow. Thus, while the temperature climbed only somewhat more than double, the intensity of the radiation increased from 10.4 to 122; thus, almost 12-fold.)
See also:
- Wisniak, Jaime (November 2002). «Heat radiation law – from Newton to Stefan». Indian Journal of Chemical Technology. 9: 545–555. ; see pp. 551–552. Available at: National Institute of Science Communication and Information Resources (New Delhi, India)
^ Stefan, J. (1879). «Über die Beziehung zwischen der Wärmestrahlung und der Temperatur» [On the relation between heat radiation and temperature]. Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften: Mathematisch-Naturwissenschaftliche Classe (Proceedings of the Imperial Philosophical Academy [of Vienna]: Mathematical and Scientific Class) (in German). 79: 391–428.
^ Stefan stated (Stefan, 1879), p. 421: «Zuerst will ich hier die Bemerkung anführen, … die Wärmestrahlung der vierten Potenz der absoluten Temperatur proportional anzunehmen.» (First of all, I want to point out here the observation which Wüllner, in his textbook, added to the report of Tyndall’s experiments on the radiation of a platinum wire that was brought to glowing by an electric current, because this observation first caused me to suppose that thermal radiation is proportional to the fourth power of the absolute temperature.)
^ Boltzmann, Ludwig (1884). «Ableitung des Stefan’schen Gesetzes, betreffend die Abhängigkeit der Wärmestrahlung von der Temperatur aus der electromagnetischen Lichttheorie» [Derivation of Stefan’s law, concerning the dependency of heat radiation on temperature, from the electromagnetic theory of light]. Annalen der Physik und Chemie (in German). 258 (6): 291–294. Bibcode:1884AnP…258..291B. doi:10.1002/andp.18842580616.
^ Massimiliano Badino, The Bumpy Road: Max Planck from Radiation Theory to the Quantum (1896–1906) (2015), p. 31.
^ Sloane, N. J. A. (ed.). «Sequence A081820». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
^ Moldover, M. R.; Trusler, J. P. M.; Edwards, T. J.; Mehl, J. B.; Davis, R. S. (1988-01-25). «Measurement of the Universal Gas Constant R Using a Spherical Acoustic Resonator». Physical Review Letters. 60: 249. doi:10.1103/PhysRevLett.60.249.
^ Çengel, Yunus A. (2007). Heat and Mass Transfer: a Practical Approach (3rd ed.). McGraw Hill.
^ (Stefan, 1879), pp. 426–427.
^ Soret, J.L. (1872) «Comparaison des intensités calorifiques du rayonnement solaire et du rayonnement d’un corps chauffé à la lampe oxyhydrique» [Comparison of the heat intensities of solar radiation and of radiation from a body heated with an oxy-hydrogen torch], Archives des sciences physiques et naturelles (Geneva, Switzerland), 2nd series, 44: 220–229; 45: 252–256.
^ Waterston, John James (1862). «An account of observations on solar radiation». Philosophical Magazine. 4th series. 23 (2): 497–511. Bibcode:1861MNRAS..22…60W. doi:10.1093/mnras/22.2.60. On p. 505, the Scottish physicist John James Waterston estimated that the temperature of the sun’s surface could be 12,880,000°.
^
See:
- Pouillet (1838). «Mémoire sur la chaleur solaire, sur les pouvoirs rayonnants et absorbants de l’air atmosphérique, et sur la température de l’espace» [Memoir on solar heat, on the radiating and absorbing powers of the atmospheric air, and on the temperature of space]. Comptes Rendus (in French). 7 (2): 24–65. On p. 36, Pouillet estimates the sun’s temperature: » … cette température pourrait être de 1761° … « ( … this temperature [i.e., of the Sun] could be 1761° … )
- English translation: Pouillet (1838) «Memoir on the solar heat, on the radiating and absorbing powers of atmospheric air, and on the temperature of space» in: Taylor, Richard, ed. (1846) Scientific Memoirs, Selected from the Transactions of Foreign Academies of Science and Learned Societies, and from Foreign Journals. vol. 4. London, England: Richard and John E. Taylor. pp. 44–90; see pp. 55–56.
^ «Luminosity of Stars». Australian Telescope Outreach and Education. Retrieved 2006-08-13.
^ Intergovernmental Panel on Climate Change Fourth Assessment Report. Chapter 1: Historical overview of climate change science Archived 2018-11-26 at the Wayback Machine page 97
^ Solar Radiation and the Earth’s Energy Balance
^ «Introduction to Solar Radiation». Newport Corporation. Archived from the original on October 29, 2013.
^ Knizhnik, Kalman. «Derivation of the Stefan–Boltzmann Law» (PDF). Johns Hopkins University – Department of Physics & Astronomy. Archived from the original (PDF) on 2016-03-04. Retrieved 2018-09-03.
^ (Wisniak, 2002), p. 554.
^ Lemons, Don S.; Shanahan, William R.; Buchholtz, Louis J. (2022-09-13). On the Trail of Blackbody Radiation: Max Planck and the Physics of his Era. MIT Press. p. 38. ISBN 978-0-262-37038-7.
^ Campana, S.; Mangano, V.; Blustin, A. J.; Brown, P.; Burrows, D. N.; Chincarini, G.; Cummings, J. R.; Cusumano, G.; Valle, M. Della; Malesani, D.; Mészáros, P.; Nousek, J. A.; Page, M.; Sakamoto, T.; Waxman, E. (August 2006). «The association of GRB 060218 with a supernova and the evolution of the shock wave». Nature. 442 (7106): 1008–1010. doi:10.1038/nature04892. ISSN 0028-0836.

References[edit]

Stefan, J. (1879), «Über die Beziehung zwischen der Wärmestrahlung und der Temperatur» [On the relationship between heat radiation and temperature] (PDF), Sitzungsberichte der Mathematisch-naturwissenschaftlichen Classe der Kaiserlichen Akademie der Wissenschaften (in German), 79: 391–428
Boltzmann, L. (1884), «Ableitung des Stefan’schen Gesetzes, betreffend die Abhängigkeit der Wärmestrahlung von der Temperatur aus der electromagnetischen Lichttheorie» [Derivation of Stefan’s little law concerning the dependence of thermal radiation on the temperature of the electro-magnetic theory of light], Annalen der Physik und Chemie (in German), 258 (6): 291–294, Bibcode:1884AnP…258..291B, doi:10.1002/andp.18842580616

Источник

Действие закона Стефана-Больцмана

Закон Стефана-Больцмана: совместимость абсолютно черного тела пропорциональна четвертой степени его температуры.

Тела, нагретые до какой-то температуры, способны излучать энергию. Она состоит из электромагнитных волн с различной длиной. Выражение «раскален докрасна» означает, что температура объекта настолько велика, что тепловое излучение происходит в видимой, световой области спектра. При рассмотрении тел на атомарном уровне возбужденные атомы испускают фотоны, которые формируют излучение.

Действие закона Стефана-Больцмана можно объяснить с помощью рассмотрения атома, который излучает свет в недрах Солнца. Свет будет поглощен мгновенно другим атомом и излучен им повторно. Таким образом, потенциальный свет будет перемещаться между атомами по цепочке. Для такой системы характерно энергетическое равновесие.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Равновесному состоянию можно дать следующее обозначение:

Свет со строго определенной частотой будет поглощен одним атомом в одной точке.
Одновременно будет наблюдаться испускание света с такой же частотой другим атомом в другой точке.
Показатели интенсивности света каждой длины волны спектра остаются стабильными.

Внутри Солнца наблюдается падение температуры с удалением от центра звезды. Если двигаться на поверхность, то можно отметить более высокие температуры светового излучения по сравнению с температурой окружающей среды, соответствующие определенному спектру. В итоге, повторное излучение, исходя из закона Стефана-Больцмана, характеризуется более низкими энергиями и частотами.

Однако, согласно закону сохранения энергии, количество излучаемых фотонов будет увеличиваться. Таким образом, на момент достижения излучением поверхности звезды спектральное распределение будет определено в соответствии с температурой поверхности Солнца, то есть около 5 800 К, а не температурой центра Солнца, которая составляет примерно 15 000 000 К.

История открытия

Данная закономерность была сформулирована в 1879 году физиком из Австрии Йозефом Стефаном. Основанием для открытия послужили экспериментальные измерения. Непосредственно сами опыты были проведены ирландским физиком Джоном Тиндалем.

В 1884 году Людвиг Больцман проводил теоретические исследования с применением термодинамики. В результате ученый пришел к этому закону изучения черного тела. Рассуждения Больцмана были построены на изучении некого идеального двигателя, в качестве энергетического источника которого использовался свет. Экспериментально подтвержденный закон был опубликован Стефаном в статье с названием «Об отношении между излучением и абсолютной температурой», которая была включена в одну из брошюр Академии наук Вены.

Концепция черного тела

Черное тело — теоретический объект, обладающий способностью к поглощению абсолютно всей электромагнитной энергии, попадающей на его поверхность.

Закономерность Стефана-Больцмана справедлива при условии наблюдения за абсолютно черным телом, которое поглощает излучение, попадающее на поверхность, в полном объеме. В реальном мире физические объекты способны поглощать лишь какую-то часть лучевой энергии. Остальное излучение отражается от их поверхности.

Следует отметить, что закон, исходя из которого удельная мощность излучения с их поверхности пропорциональна Т4, работает и при реальных условиях. Только в данной ситуации необходимо постоянную Больцмана заменить на другой коэффициент, отражающий характеристики реального физического объекта. Определить такую константу можно с помощью эксперимента.

Математическая формула закона излучения

Энергия, поступая к поверхности Солнца или любого другого горячего объекта, отражается от него в виде излучения. Определить характер излученной энергии позволяет закон Стефана-Больцмана. В виде формулы закономерность записывают в следующем виде:

(E=sigma T^{4})

Где Т является температурой и измеряется в Кельвинах, σ представляет собой постоянную Больцмана.

Согласно уравнению, можно сделать вывод, что повышение температуры сопровождается увеличением светимости тела в значительно большей степени. При повышении температуры объекта в 2 раза, его светимость увеличится в 16 раз.

Использование закона Стефана-Больцмана

Йозеф Стефан применил самостоятельно открытый закон на практике. С помощью выведенной закономерности ученому удалось определить температуру, которой обладает поверхность Солнца. Стефан использовал данные Чарльза Сорета, в которых указано, что величина плотности потока солнечной энергии в 29 раз превышает аналогичные показатели электромагнитного излучения нагретой пластины из металла. Ученый разместил пластину от датчика электромагнитного излучения под тем же углом, под которым видно Солнце с нашей планеты. Результаты эксперимента Сорета оценивали температуру пластины в 1900-2000 градусов.

В опыте Йозефа Стефана было учтено, что солнечное излучение поглощается атмосферой на Земле. По его предположению, поток энергии от звезды в реальных условиях в 43,5 раз превышает аналогичные показатели нагретой пластины. Данное исследование послужило началом для ряда экспериментов по измерению точного атмосферного поглощения энергии от Солнца, которые проводились в период с 1888 по 1904 года.

Исходя из закона Стефана-Больцмана, достаточно просто прийти к выводу, что температура на поверхности нашей звезды превышает температуру металлической пластины в 2,57 раза. Расчет выполняется с помощью извлечения корня четвертой степени от отношения потоков энергии Солнца и пластины. По итогам эксперимента Стефан вычислил, что температура поверхности звезды составляет 5712 К. Стоит отметить, что по современным данным данный показатель равен 5780 К.

Источник

Как вы измеряете температуру своего тела? Самый простой ответ — «с помощью термометра». Но так ли это и со звездами? Ответ — большое НЕТ. Как известно, температура звезды может достигать нескольких тысяч Кельвинов. Но на сегодняшний день нет такого термометра, который выдерживал бы такие высокие температуры. Более того, даже если такой термометр со сверхмощными способностями существует, кто будет использовать его на звездах в миллионы световых лет от нас? Итак, как мы измеряем температуру звезд?

Здесь нам на помощь приходят косвенные методы. Чтобы преодолеть вышеупомянутые проблемы, астрофизики используют ряд косвенных методов измерения температуры. Давайте посмотрим на некоторые из них по очереди!

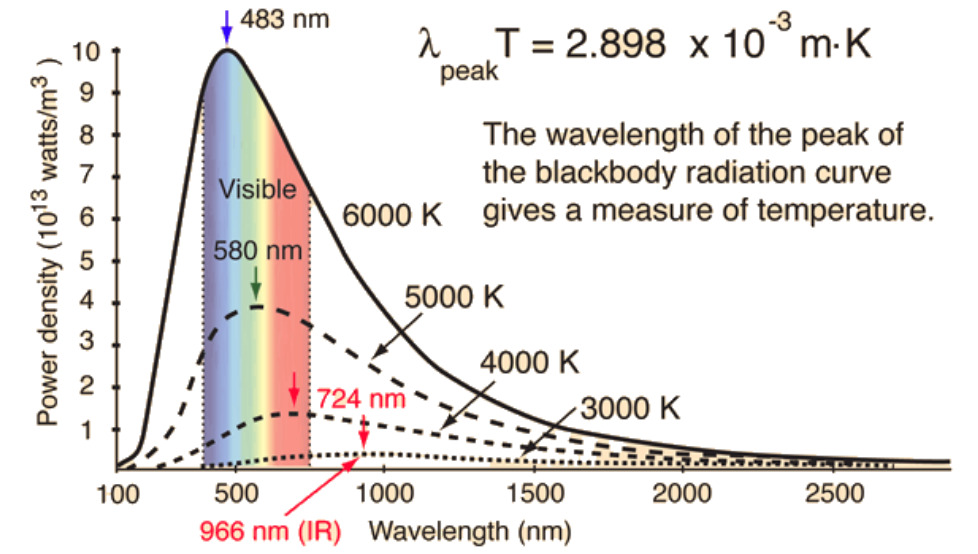
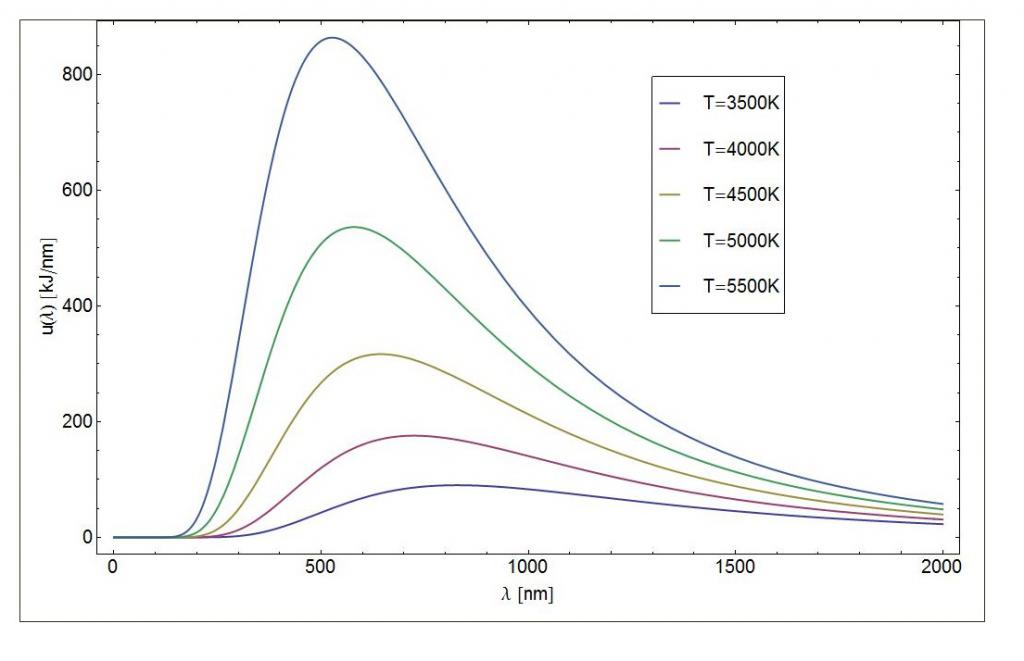
Закон смещения Вина

Закон смещения Вина касается спектра излучения черного тела. В соответствии с этим кривая излучения черного тела для разных температур будет иметь пик на разных длинах волн, которые обратно пропорциональны температуре. Используя эту обратную зависимость между длиной волны и температурой, можно оценить температуры звезд.

Однако это применимо только к звездам, у которых спектр очень близок к спектру черного тела. Более того, должны быть доступны также спектры, откалиброванные по потоку рассматриваемой звезды. Однако этот метод не дает очень точных результатов, поскольку звезды, как правило, не являются черными телами.

Закон Стефана — Больцмана

Еще один закон, который можно использовать для измерения температуры звезд, — это закон Стефана — Больцмана. Закон Стефана – Больцмана описывает мощность, излучаемую черным телом, с точки зрения его температуры. Согласно этому закону, общая лучистая тепловая мощность, излучаемая поверхностью, пропорциональна четвертой степени ее абсолютной температуры. L = 4πR² σT⁴. Здесь σ — постоянная Стефана-Больцмана, L — светимость, R и T — радиус и температура рассматриваемой звезды.

Сначала мы измеряем полный поток света, исходящего от звезды. Объединив эти факторы, ученые оценивают светимость. А с помощью интерферометров можно определить радиус звезды. В конце концов, температура измеряется путем включения всех этих членов в формулу Стефана — Больцмана. Ограничивающим фактором здесь является сложность измерения радиусов самых больших или ближайших звезд. Таким образом, измерения существуют только для нескольких гигантов и нескольких десятков ближайших звезд главной последовательности. Однако они действуют как фундаментальные калибраторы, с которыми астрофизики сравнивают и калибруют другие методы.

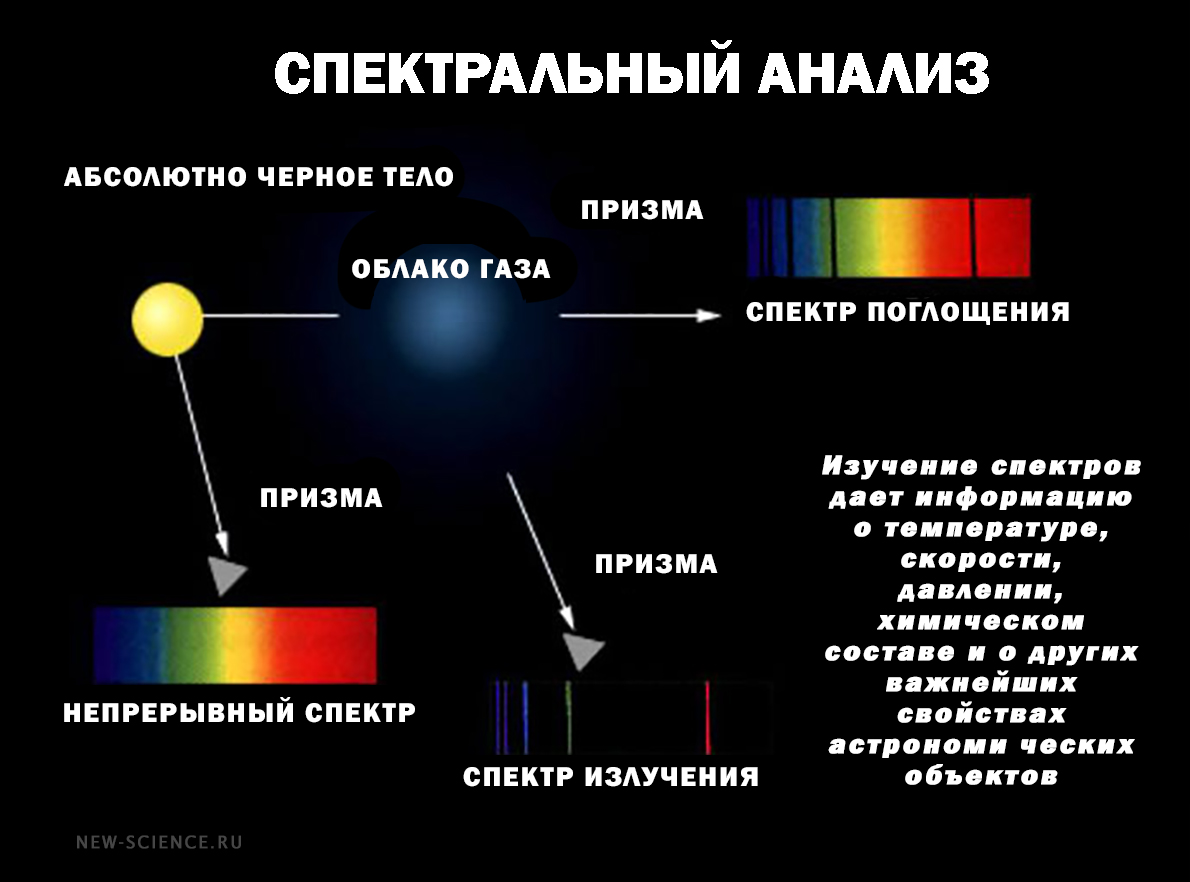
По спектральному анализу звезды

Мы знаем, что атомы/ионы имеют разные уровни энергии. И численность этих уровней зависит от температуры. И население этих уровней зависит от температуры. Более высокие уровни заняты при более высоких температурах и наоборот — при более низких. Переходы между уровнями могут привести к излучению или поглощению света на определенной длине волны в зависимости от разницы в энергии между соответствующими уровнями. Как правило, звезда горячее внутри и холоднее снаружи. Более холодные вышележащие слои поглощают излучение, исходящее из центра звезды. Это приводит к появлению линий поглощения в полученном нами спектре.

Спектральный анализ состоит из измерения силы этих линий поглощения для различных химических элементов и разных длин волн. Сила линии поглощения зависит в первую очередь от температуры звезды и количества конкретного химического элемента. Однако на нее могут влиять и некоторые другие параметры, такие как гравитация, турбулентность, структура атмосферы и т.д. Этот метод дает температурные измерения с точностью до +/-50 Кельвинов.

Взаимосвязь цвета и температуры

Еще один метод измерения температуры звезд — анализ их цвета. Хотя все звезды кажутся белыми, при внимательном рассмотрении они имеют разные цвета. Вариации являются результатом их температуры. Холодные звезды кажутся красными, а горячие — синими. Мы измеряем цвет звезды с помощью прибора, называемого фотоэлектрическим фотометром.

Это включает в себя пропускание света через различные фильтры и определение количества, которое проходит через каждый фильтр. Измерения фотометра преобразуются в температуру с использованием стандартных шкал. Этот метод очень полезен, когда хороший спектр звезды недоступен. Результаты, полученные этим методом, имеют точность до +/- 100-200 К. Однако этот метод дает плохие результаты для более холодных звезд.

Каждый из вышеупомянутых методов имеет свои преимущества и недостатки. Тем не менее астрофизики во всем мире широко используют эти методы, и в конечном итоге дают удовлетворительные результаты.

Источник

Закон Стефана-Больцмана связан с тепловыми явлениями и процессами излучения в физике. Согласно этому закону излучатель, который представляет собой абсолютно черное тело, испускает энергию в виде электромагнитного излучения, пропорциональную четвертой степени абсолютной температуры, за одну секунду с единицы площади своей поверхности.

Понятие о черном теле

Прежде чем описывать закон излучения Стефана-Больцмана, следует разобраться в вопросе о том, что представляет собой черное тело. Черное тело является теоретическим объектом, который способен поглощать абсолютно всю электромагнитную энергию, которая падает на него. То есть электромагнитное излучение не проходит через черное тело и не отражается от него. Не следует путать черное тело с темной материей в космосе, поскольку черное тело способно излучать электромагнитную энергию. Концепция черного тела введена в физику для упрощения изучения процессов излучения реальных тел. Сам термин «черное тело» был введен Густавом Кирхгофом в 1862 году.

Излучение тел

Каждое реальное тело излучает энергию в виде электромагнитных волн в окружающее пространство. При этом в соответствии с законом Стефана-Больцмана это излучение будет тем интенсивнее, чем выше температура тела. Если тело имеет невысокую температуру, например температуру окружающей среды, то излучаемая им энергия невелика и большая ее часть испускается в виде длинных электромагнитных волн (инфракрасное излучение). Увеличение температуры тела приводит не только к увеличению количества излучаемой энергии, но и к смещению спектра излучения в область более высоких частот. Именно поэтому цвет тела изменяется при его нагреве. Количество энергии, которое испускает тело, нагретое до некоторой конкретной температуры в определенном узком интервале частот, описывается законом Планка.

Количество и спектр излучаемой электромагнитной энергии зависят не только от температуры тела, но и от природы излучающей поверхности. Так, матовая или черная поверхность обладает большей излучающей способностью, чем светлая или блестящая. Это означает, что количество энергии, которое излучает раскаленная углеродная нить, больше, чем, например, нить из платины, нагретая до той же температуры. Закон Кирхгофа устанавливает, что если тело хорошо излучает энергию, значит, оно будет и хорошо ее поглощать. Таким образом, тела черного цвета являются хорошими поглотителями электромагнитного излучения.

Реальные объекты, близкие по своим характеристикам к черному телу

Излучательная и поглощательная способности черного тела являются идеализированным случаем, однако в природе существуют объекты, которые по этим характеристикам в первом приближении можно считать черным телом.

Самым простым объектом, который по своей способности поглощать видимый свет близок к черному телу, является изолированная емкость, имеющая небольшое отверстие в своем корпусе. Через это отверстие луч света попадает в полость объекта и испытывает многократное отражение от внутренних стенок емкости. При каждом отражении часть энергии луча поглощается, и этот процесс продолжается до тех пор, пока вся энергия не будет поглощена.

Еще одним объектом, который практически полностью поглощает падающий на него свет, является сплав никеля и фосфора. Получен этот сплав был в 1980 году индусами и американцами, а в 1990 году он был усовершенствован японскими учеными. Этот сплав отражает всего 0,16 % падающей на него световой энергии, что в 25 раз меньше, чем аналогичная величина для самой черной краски.

Реальным примером излучателя в космосе, который по своим свойствам близок к излучающей способности черного тела, являются звезды галактик.

Энергия излучения черного тела

В соответствии с определением закона Стефана-Больцмана энергия излучения черного тела с поверхности 1 м² за одну секунду определяется по формуле:

E = σ (T_э)⁴,

где T_э — эффективная температура излучения, то есть абсолютная температура поверхности тела, σ — постоянная Стефана-Больцмана, равная 5,67·10^-8 Вт/(м²·К⁴).

Чем ближе излучательные характеристики реальных тел к свойствам черного тела, тем ближе будет энергия, рассчитанная по указанной формуле, к излучаемой энергии реальных тел.

Энергия излучения реальных тел

Формула закона Стефана-Больцмана для излучения реальных тел имеет вид:

E = εσ (T_э)⁴,

где ε — коэффициент излучательной способности реального тела, который лежит в пределах 0<ε<1. Этот коэффициент не является постоянной величиной, а зависит от абсолютной температуры, частоты электромагнитного излучения и свойств поверхности реального тела.

История открытия закона Стефана-Больцмана

Этот закон был открыт в 1879 году австрийским физиком Йозефом Стефаном на основании экспериментальных измерений. Сами эксперименты были выполнены ирландским физиком Джоном Тиндалем. В 1884 году Людвиг Больцман в результате теоретических исследований с использованием термодинамики пришел также к этому закону излучения черного тела. В своих рассуждениях Больцман рассматривал некоторый идеальный двигатель, в котором источником энергии был свет.

Стефан опубликовал полученный им экспериментально закон в статье под названием «Об отношении между излучением и абсолютной температурой» в одной из брошюр Академии наук Вены.

Математический вывод формулы закона излучения

Вывод формулы закона Стефана-Больцмана достаточно прост, для этого нужно всего лишь проинтегрировать по всем частотам энергию, которая определяется законом Планка для излучения черного тела. В результате такого интегрирования можно показать, что константа Стефана-Больцмана определяется через другие фундаментальные физические постоянные:

σ = 2pi⁵k⁴/(15c²h³),

здесь pi = 3,14 (число пи), k = 1,38·10^–²³ Дж/К (постоянная Больцмана), c = 3·10⁸ м/с (скорость света в вакууме), h = 6,63·10^-34 Дж·с (постоянная Планка).

В результате вычислений получаем, что σ = 5,67·10^-8 Вт/(м²·К⁴), что точно соответствует экспериментально определенному значению.

Пример использования закона Стефана-Больцмана: температура поверхности Солнца

Используя самостоятельно открытый закон, Стефан определил температуру поверхности нашей звезды — Солнца. Для этого он использовал данные Чарльза Сорета, согласно которым плотность потока солнечной энергии в 29 раз больше, чем плотность электромагнитного излучения нагретой металлической пластины. Пластину ученый расположил от детектора электромагнитного потока под тем же углом, под которым видно Солнце с Земли. В результате Сорет оценил температуру пластины в 1900-2000 °C. Стефан, в свою очередь, также учел атмосферное поглощение солнечного излучения на Земле, предположив, что реальный поток энергии от Солнца в 43,5 раза больше такового от нагретой пластины. Отметим, что точные измерения атмосферного поглощения солнечной энергии были проведены в серии экспериментов с 1888 по 1904 год.

Далее, согласно закону Стефана-Больцмана можно легко показать, что температура поверхности Солнца должна быть больше температуры металлической пластины в 2,57 раза (для получения этой цифры необходимо взять корень четвертой степени от отношения энергетических потоков излучения Солнца и пластины). Таким образом, Стефан получил, что температура поверхности нашей звезды равна 5713 К (современное значение составляет 5780 К).

Полученное значение температуры поверхности Солнца являлось самым точным в XIX веке. До работ Стефана другие ученые получали как слишком низкие температуры для поверхности Солнца (1800 °C), так и слишком высокие ее значения (13 000 000 °C).

Источник

Светимость абсолютно черного тела пропорциональна четвертой степени его температуры.

Нагретые тела излучают энергию в виде электромагнитных волн различной длины. Когда мы говорим, что тело «раскалено докрасна», это значит, что его температура достаточно высока, чтобы тепловое излучение происходило в видимой, световой части спектра. На атомарном уровне излучение становится следствием испускания фотонов возбужденными атомами (см. Излучение черного тела). Закон, описывающий зависимость энергии теплового излучения от температуры, был получен на основе анализа экспериментальных данных австрийским физиком Йозефом Стефаном и теоретически обоснован также австрийцем Людвигом Больцманом (см. Постоянная Больцмана).

Чтобы понять, как действует этот закон, представьте себе атом, излучающий свет в недрах Солнца. Свет тут же поглощается другим атомом, излучается им повторно — и таким образом передается по цепочке от атома к атому, благодаря чему вся система находится в состоянии энергетического равновесия. В равновесном состоянии свет строго определенной частоты поглощается одним атомом в одном месте одновременно с испусканием света той же частоты другим атомом в другом месте. В результате интенсивность света каждой длины волны спектра остается неизменной.

Температура внутри Солнца падает по мере удаления от его центра. Поэтому, по мере движения по направлению к поверхности, спектр светового излучения оказывается соответствующим более высоким температурам, чем температура окружающий среды. В результате, при повторном излучении, согласно закону Стефана—Больцмана, оно будет происходить на более низких энергиях и частотах, но при этом, в силу закона сохранения энергии, будет излучаться большее число фотонов. Таким образом, к моменту достижения им поверхности спектральное распределение будет соответствовать температуре поверхности Солнца (около 5 800 К), а не температуре в центре Солнца (около 15 000 000 К).

Энергия, поступившая к поверхности Солнца (или к поверхности любого горячего объекта), покидает его в виде излучения. Закон Стефана—Больцмана как раз и говорит нам, какова излученная энергия. Этот закон записывается так:

E = σT ⁴

где Т — температура (в кельвинах), а σ — постоянная Больцмана. Из формулы видно, что при повышении температуры светимость тела не просто возрастает — она возрастает в значительно большей степени. Увеличьте температуру вдвое, и светимость возрастет в 16 раз!

Итак, согласно этому закону любое тело, имеющее температуру выше абсолютного нуля, излучает энергию. Так почему, спрашивается, все тела давно не остыли до абсолютного нуля? Почему, скажем, лично ваше тело, постоянно излучая тепловую энергию в инфракрасном диапазоне, характерном для температуры человеческого тела (чуть больше 300 К), не остывает?

Ответ на этот вопрос, на самом деле, состоит из двух частей. Во-первых, с пищей вы получаете энергию извне, которая в процессе метаболического усвоения пищевых калорий организмом преобразуется в тепловую энергию, восполняющую потери вашим телом энергии в силу закона Стефана—Больцмана. Умершее теплокровное весьма быстро остывает до температуры окружающей среды, поскольку энергетическая подпитка его тела прекращается.

Еще важнее, однако, тот факт, что закон распространяется на все без исключения тела с температурой выше абсолютного нуля. Поэтому, отдавая свою тепловую энергию окружающей среде, не забывайте, что и тела, которым вы отдаете энергию, — например, мебель, стены, воздух, — в свою очередь излучают тепловую энергию, и она передается вам. Если окружающая среда холоднее вашего тела (как чаще всего бывает), ее тепловое излучение компенсирует лишь часть тепловых потерь вашего организма, и он восполняет дефицит за счет внутренних ресурсов. Если же температура окружающей среды близка к температуре вашего тела или выше нее, вам не удастся избавиться от избытка энергии, выделяющейся в вашем организме в процессе метаболизма посредством излучения. И тут включается второй механизм. Вы начинаете потеть, и вместе с капельками пота через кожу покидают ваше тело излишки теплоты.

В вышеприведенной формулировке закон Стефана—Больцмана распространяется только на абсолютно черное тело, поглощающее всё попадающее на его поверхность излучение. Реальные физические тела поглощают лишь часть лучевой энергии, а оставшаяся часть ими отражается, однако закономерность, согласно которой удельная мощность излучения с их поверхности пропорциональна Т ⁴, как правило, сохраняется и в этом случае, однако постоянную Больцмана в этом случае приходится заменять на другой коэффициент, который будет отражать свойства реального физического тела. Такие константы обычно определяются экспериментальным путем.

Источник

History[edit]

Examples[edit]

Temperature of the Sun[edit]

Temperature of stars[edit]

Effective temperature of the Earth[edit]

Origination[edit]

Thermodynamic derivation of the energy density[edit]

Derivation from Planck’s law[edit]

Energy density[edit]

See also[edit]

Notes[edit]

References[edit]

Действие закона Стефана-Больцмана

История открытия

Концепция черного тела

Математическая формула закона излучения

Использование закона Стефана-Больцмана

Закон смещения Вина

Закон Стефана — Больцмана

По спектральному анализу звезды

Взаимосвязь цвета и температуры

Понятие о черном теле

Излучение тел

Реальные объекты, близкие по своим характеристикам к черному телу

Энергия излучения черного тела

Энергия излучения реальных тел

История открытия закона Стефана-Больцмана

Математический вывод формулы закона излучения

Пример использования закона Стефана-Больцмана: температура поверхности Солнца