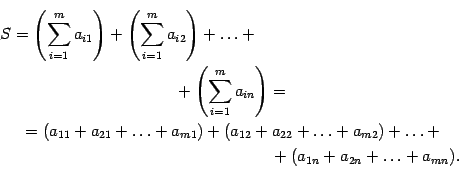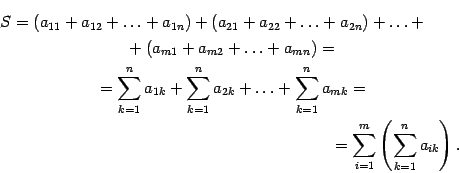Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.
Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.
Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.
Знак Σ — сумма
Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:
Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.
На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:
- Взять все числа от 5 до 15 (снизу и сверху знака Σ).
- С каждым из этих чисел сделать то, что написано справа от Σ, — то есть умножить на два.
- Сложить результаты этих операций.
Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».
Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:
Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Что дальше
Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.
Вёрстка:
Кирилл Климентьев
Решение высшей математики онлайн
‹— Назад
В математике для записи сумм, содержащих много слагаемых, или в случае, когда число слагаемых обозначено буквой, применяется следующая запись:
которая расшифровывается так
где — функция целочисленного аргумента. Здесь символ (большая греческая буква «сигма») означает суммирование. Запись внизу символа суммирования показывает, что переменная, которая меняет свои значения от слагаемого к слагаемому, обозначена буквой и что начальное значение этой переменной равно . Запись вверху обозначает последнее значение, которое принимает переменная .
Пример 14.2 Вычислим несколько сумм:
1) .
2) . Так как в правой части стоит сумма геометрической прогрессии с первым членом равным и знаменателем прогрессии равным , то эту сумму легко найти
3) .
4) .
5) .
В курсе линейной алгебры чаще всего будут встречаться суммы вида . Здесь переменная с индексом рассматривается как функция от своего индекса. Поэтому
С помощью знака суммы формулу (10.1) скалярного произведения векторов можно записать так:
где для трехмерного пространства , для плоскости .
Для единообразия будем считать, что
и говорить, что это сумма, содержащая одно слагаемое.
Замечание 14.1 Буква, стоящая внизу под знаком суммы (индекс суммирования), не влияет на результат суммирования. Важно лишь, как от этого индекса зависит суммируемая величина. Например,
Или
в правой части никакой буквы нет, значит, и результат от не зависит.
Предложение 14.1 Множитель, не зависящий от индекса суммирования, может быть вынесен за знак суммы:
Доказательство этого предложения предоставляется читателю.
Предложение 14.2
Это предложение является частным случаем следующего утверждения.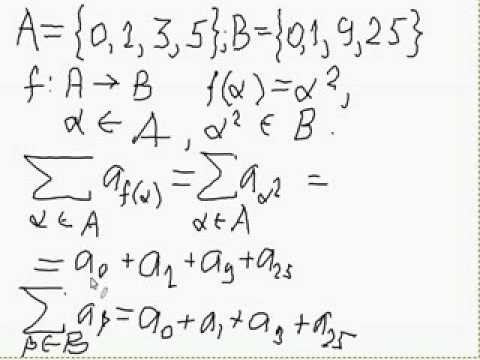
Предложение 14.3
Доказательство. Пусть
Тогда
Раскроем скобки в правой части этого равенства. Получим сумму элементов при всех допустимых значениях индексов суммирования. Слагаемые сгруппируем по-другому, а именно, сначала соберем все слагаемые, у которых первый индекс равен 1, потом, у которых первый индекс равен 2 и т.д. Получим
Заменив в этом равенстве в левой части его выражением через знаки суммирования, получим формулу (14.4).
Замечание 14.2 Двойные суммы из равенства (14.4) можно записывать и без использования скобок
Нужно помнить, что двойная сумма означает сумму элементов для всех допустимых значений индексов суммирования.
Если границы изменения всех индексов суммирования одинаковы, то можно для суммирования по нескольким индексам использовать запись вида
Иногда под символом суммы указывают дополнительные условия, налагаемые на индексы суммирования. Так запись
означает, что в сумму не включаются величины , ,…, , то есть с равными индексами.
Иногда в записи суммы не указываются границы изменения индексов, например,
Такая запись используется, когда значения, которые могут принимать индексы, очевидны из предыдущего текста или будут оговорены сразу после окончания формулы.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
определение и свойства.

ЛЕКЦИЯ № 1
1.
Символ
В
математике часто приходится рассматривать сумму большого числа слагаемых. Для
таких сумм введено следующее обозначение:
Индекс
называется индексом суммирования. В
качестве индекса суммирования может быть употреблена и любая другая буква.
Имеют
место следующие правила обращения со знаком суммы ,
1.
Обозначение индекса суммирования
может быть изменено
2.
Множитель, не зависящий от
индекса суммирования, может быть вынесен за знак суммы:
3.
Два знака суммы могут быть
переставлены
Доказательство
приведенных правил легко доказывается на основании введенного символа
суммирования. Для примера доказательства докажем правило 2.
Что и требовалось доказать.
2.
Детерминанты.
Определение и
свойства
Определение. Матрицей размеров называется
совокупность чисел, расположенных в виде таблицы из строк и столбцов:
Числа , составляющие матрицу, называются элементы
матрицы и
обозначаются буквами с двумя индексами,
первый из них обозначает номер строки,
а второй – номер столбца. Если число строк
в матрице равно числу столбцов, то матрица называется квадратной. Если же число
строк в матрице неравно числу столбцов, то матрица называется прямоугольной.
Детерминантом
(определителем) матрицы мы будем обозначать или,
Определение.
Детерминант квадратной матрицы – это
число, которое ставится в соответствие матрице и может быть вычислено по ее
элементам по формуле.
— элементы матрицы
— алгебраическое дополнение
соответствующего элемента матрицы, которое вычисляется по формуле
где —
минор соответствующего элемента
матрицы.
Определение.
Минор это детерминант матрицы
порядка , полученной из вычеркиванием
строки и -го
столбца.
Определение.
Матрица порядка 1 состоит из
одного числа, и ее детерминант по определению считают равным этому числу.
На
первый взгляд это определение может показаться не эффективным: детерминант
матрицы порядка определяется через детерминанты
матрицы порядка , а эти детерминанты сами не
определены. В действительности же в этом ничего, плохого нет. Для определения
чисел мы можем воспользоваться той же формулой,
поскольку она имеет место для матриц любого порядка. Тем самым мы выразим через детерминанты матриц порядка . Можно продолжать этот процесс, пока мы не
придем к матрицам первого порядка, а для них детерминант определен
непосредственно.
Применим
наше определение к матрицам 2 – го порядка.
Единичной
матрицей называется матрица.
Для
нее , так как, раскрывая определитель по определению,
мы получаем и так далее.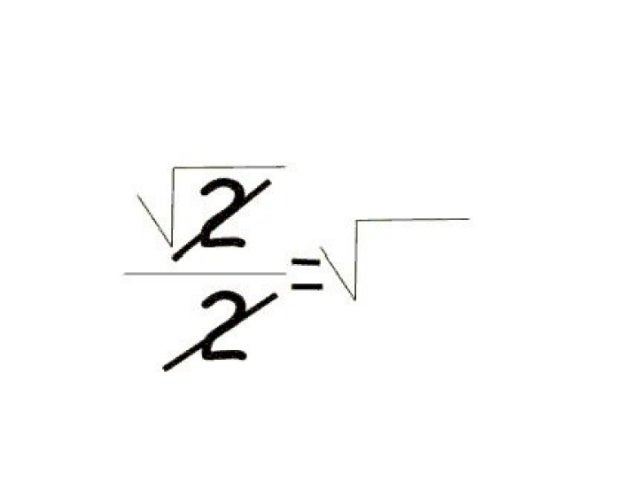
Определение.
Если в матрице поменять местами строки и столбцы, то
полученная матрица будет называться
транспонированной, а переход от к — транспонирование.
Матрицу,
полученную из матрицы транспонированием, обозначают .
Сформулируем
одну очень важную теорему в теории определителей.
Теорема. Для каждой квадратной матрицы
порядка имеет место формула
или
Эти
формулы называются формулами разложения детерминанта соответственно по
строке и по столбцу.
Доказательство:
Доказательство мы проведем методом полной индукции. Начнем с первой формулы.
Непосредственно очевидно, что для матриц второго порядка она справедлива
Допустим,
что формула верна для матриц порядка , и докажем ее для
матрицы порядка.
При
любом минор рассматриваемой
матрицы есть детерминант некоторой матрицы порядка , в которую входит (без своего элемента) -я строка матрицы .
Пользуясь предположением индукции, мы можем разложить по
этой строке.
Минор получен
из матрицы вычеркиванием 1-й и -й
строк и -го и -го
столбцов, таким образом у нас . И мы получим, поменяв
порядок суммирования
Что и требовалось доказать.
Доказательство
второй формулы теоремы совершенно аналогично проведенному доказательству и
провести его, мы предоставляем читателю.
Свойства
детерминантов.
Свойство
1. Для любой квадратной матрицы
Доказательство:
Доказательство мы проведем методом полной индукции. Начнем с первой формулы.
Непосредственно очевидно, что для матриц второго порядка она справедлива
Допустим,
что формула верна для матриц порядка , и докажем ее для
матрицы порядка.
Пусть
матрица, получаемая из вычеркиванием -й
строки и -го столбца, а матрица , получаемая из вычеркиванием
-й строки и -го
столбца. Легко видеть, что, . Поэтому из
предложения индукции следует, что , или, словами,
дополнительный минор элемента в матрице равен дополнительному минору элемента в матрице .
того, , и разложение по -й строке совпадает с разложением по -му столбцу.
Свойство доказано.
Символ суммы в ворде
Знак суммы один из востребованных элементов в математике, часто он и используется в программе ворд, для написания разнообразных формул в ТЗ, курсовых.
В программе ворд, можно поставить пять видов знаков суммы, рассмотрим подробную инструкцию, как их можно поставить:
Первый шаг. Откроем новую книгу, на верхней панели выберем закладку «Вставка», в которой ищем блок с настройками (находиться в самом правом углу) «Символы» и нажимаем на иконку с надписью «Формула». Чтобы на экране появилось специальное меню.
Второй шаг. Проваливаемся в это специальное меню, а в конструкторе формул находим иконку с подписью «Крупный оператор» и нажимаем на него. После чего на экране появиться выбор знаков суммы.
Для данного примера, я выбрал второй знак суммы, а вы можете поставить тот, который подходить для решения вашей конкретной задачи.
Как вы наверняка уже знаете, в Microsoft Word есть довольно-таки большой набор специальных знаков и символов, которые при необходимости можно добавить в документ через отдельное меню. О том, как это сделать, мы уже писали, и более подробно ознакомиться с данной темой вы можете в нашей статье.
Помимо всевозможных символов и знаков, в MS Word также можно вставлять различные уравнения и математические формулы, используя готовые шаблоны или создавая собственные. Об этом мы тоже писали ранее, а в данной статье хотим поговорить о том, что имеет отношение к каждой из вышеупомянутых тем: как вставить значок суммы в Ворде?
Действительно, когда необходимо добавить этот символ, становится непонятно, где его искать — в меню символов или в математических формулах. Ниже мы обо всем подробно расскажем.
Знак суммы — это математический знак, и в Ворде он расположен в разделе “Другие символы”, если точнее, в разделе “Математические операторы”.
1. Кликните в том месте, куда необходимо добавить знак суммы и перейдите во вкладку “Вставка”.
2. В группе “Символы” нажмите на кнопку “Символ”.
3. В окошке, которое появится после нажатия на кнопку, будут представлены некоторые символы, но знака суммы вы там не найдете (по крайней мере, если ранее его не использовали). Выберите раздел “Другие символы”.
4. В диалоговом окне “Символ”, которое перед вами появится, выберите из выпадающего меню набор “Математические операторы”.
5. Найдите среди открывшихся символов знак суммы и кликните по нему.
6. Нажмите “Вставить” и закройте диалоговое окно “Символ”, чтобы продолжить работу с документом.
7. Знак суммы будет добавлен в документ.
Использование кода для быстрой вставки знака суммы
У каждого символа, расположенного в разделе “Символы”, есть свой код.
Узнать код знака можно в диалоговом окне “Символ”, для этого достаточно кликнуть по необходимому знаку.
Здесь же вы найдете комбинацию клавиш, которую необходимо использовать для преобразования числового кода в необходимый символ.
1. Кликните в том месте документа, где требуется поставить знак суммы.
2. Введите код “2211” без кавычек.
3. Не перемещая курсор с этого места, нажмите клавиши “ALT+X”.
4. Введенный вами код будет заменен на знак суммы.
Вот так просто можно добавить знак суммы в Ворде. В этом же диалоговом окне вы найдете огромное количество всевозможных символов и специальных знаков, удобно отсортированных по тематическим наборам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Иногда у пользователя возникает необходимость написать в Microsoft Word математическую формулу, в которой присутствует специальный знак суммы.
1. Кликните левой кнопкой мыши в том месте, в которое собираетесь добавить знак суммы, затем перейдите во вкладку «Вставка».
2. Нажмите на иконку «Символы» в правом углу панели, затем в выпадающем списке выберите «Символ».
3. В данном окне предоставлено некоторое количество символов, отсутствующих на клавиатуре. Как видите, знака суммы тут нет, поэтому переходим в раздел «Другие символы».
4. В появившемся окне вам необходимо сменить набор символов, выбрав из выпадающего меню набор «Математические операции».
5. В появившейся коллекции определенно должен быть знак суммы — кликните по нему.
6. После выделения символа нажмите кнопку «Вставить», чтобы отразить его в нужном месте.
Использование горячих клавиш
Приятным дополнением Office Word является специальный код, присвоенный каждому символу.
Узнать данный код вы сможете в ранее открытом окне «Символ». Кликните по необходимому и увидите нужные вам данные в соответствующих полях.
1. Кликните в подходящем участке документа левом кнопкой мыши, чтобы выделить место для вставки символа.
2. Напечатайте код 2211.
3. Воспользуйтесь горячей клавишей Alt+X
4. Введенный код заменится на символ суммы.
С помощью вышеуказанных инструкций вы без проблем сможете поставить знак суммы в Ворде. Надеемся, вам помогла наша статья.
Урок математики по теме «Сумма и произведение. Знак умножения». 2-й класс
Ключевые слова:
математика,
начальная школа,
презентация,
знак умножения,
замена суммы умножением,
произведение
Цели:
- Провести исследовательскую работу с целью
знакомства с новым арифметическим действием,
выяснить приемы краткой рациональной записи
действия, отрабатывать умения делать выводы,
обобщения, раскрыть конкретный смысл действия
умножения, использовать соответствующую
терминологию, учить решать задачи при помощи
данных действий, самостоятельно выделять и
формулировать познавательную цель. - Создать условия для овладения соответствующим
вычислительным навыком; использовать фантазию,
воображение при выполнении учебных действий, а
также творческую самостоятельность, соединяя
игровую и обучающую форму деятельности,
Обеспечить выбор наиболее эффективных способов
решения задач в зависимости от конкретных
условий. - Формировать умение объяснять свой выбор,
строить фразы, отвечать на поставленный вопрос,
аргументировать. - Формировать желание выполнять учебные
действия; уверенность в своих возможностях,
аккуратность при выполнении заданий,
ответственность, любознательность, интерес к
предмету.
Планируемые результаты:
- Иметь представления о действии умножения как
сложении одинаковых слагаемых. - Знать смысл действий (операций) умножения над
целыми неотрицательными числами. -
Понимать и использовать сочетания слов «по … в
каждом…», «… раз по …», составлять числовые
выражения. Давать ответы в виде развернутых
предложений на вопросы учителя или сказочного
персонажа, уметь выполнять инструкции учителя. - Уметь в процессе учебной деятельности
контактировать с товарищами и вести диалоги.
Понимать и выполнять учебные требования,
предъявляемые со стороны учителя и
мультимедиа-персонажей.
Оборудование: смайлики для
осуществления обратной связи с учащимися,
конспект, презентация, мультимедийный проектор,
учебник, рабочая тетрадь, ТПО, черный фломастер,
карточки.
План урока:
I. Оргмомент.
II. Устный счет.
1. Карточки.
2. Задание «Бусы».
3. Группировка чисел.
4. Геометрический материал.
5. Итог устного счета.
6. Проверка индивидуальной работы.
III. Формулировка целей и задач урока.
IV. Создание проблемной ситуации.
V. Изучение нового.
VI. Закрепление.
Игра «Помоги приземлиться летчику».
VII. Физминутка.
VIII. Закрепление.
1. Работа в тетрадях (с. 92, 3).
2. Самопроверка.
3. Игра «Ёжики».
4. Задача.
5. Самопроверка.
6. Веселые задачи (устная работа).
7. Кроссворд.
IX. Итог.
X. Эмоциональный отклик.
ХОД УРОКА
Слайд 1
I. Оргмомент
Учитель.
Прозвенел, друзья, звонок.
Начинается урок.
Слайд 2
Учитель. Сегодня наш урок проводится в
необычном месте. Это кабинет информатики.
Информатика близка к математике. Она изучает не
только работу вычислительных систем, и в
частности компьютера, но и сведения из
окружающего мира.
А нам информатика поможет разобраться с
очередным секретом математики. И с нами вместе
будут проводники из мира информатики:
Слайд 3
Мышка и её друг Смайлик, который, несомненно,
вам знаком. Они помогут вам легко и быстро
познакомиться с новым материалом.
У вас на столах тоже есть Смайлик, посмотрите на
него, но он нам понадобится позже, поэтому
отложите пока его в сторону.
II. Устный счет
Учитель. Перед тем, как приступить к
изучению новой темы, нужно настроиться на
математический лад.
Отдохнуть вы все успели?
А теперь вперед – за дело.
Математика нас ждет.Начинаем устный счет.
– Пока мы будем выполнять устный счет,
некоторые ребята будут работать по карточкам
самостоятельно. Они расшифруют тему нашего
урока. Посмотрите, у кого на столах есть красные
конвертики, поднимите руку. Откройте конверт,
достаньте карточку. Вам нужно найти значение
выражений, а затем мы вместе откроем шифровку.
Задание понятно? Приступайте к выполнению.
1. Карточки.
| Ананьев | Несмашная | Стеблев | |||
|
40 – 30 |
С Е П З |
44 – 40 |
А У И Р |
66 – 6 |
Н М B О Д |
2.
Учитель. Первое задание устного счета
вам предлагает Мышка, а Смайлик будет ей
помогать.
Слайд 4
Из разных цифр собрали бусы
А в тех кружках, где чисел нет,
Поставьте минусы и плюсы,
Чтоб верный получить ответ.
– Дополняем первую ленточку бус.
Дети устно называют пример с вычислением.
– Кто не согласен с ответом, поднимите вверх
Смайлика, который лежит у вас на столах.
Дополняем вторую ленточку бус. Дополняем третью
ленточку бус. Дополняем четвертую ленточку бус.
(Проверка осуществляется с помощью
презентации)
3. Группировка чисел
Учитель. Мы посчитали, а теперь
вспомним, что мы знаем о числах.
Слайд 5
– Раздели числа на группы. Назовите группы.
– Как называются числа первой группы? (Двузначные
некруглые).
– Как называются числа второй группы? (Двузначные
круглые).
– В каком порядке стоят двузначные некруглые? (Возрастания).
– В каком порядке стоят двузначные круглые? (Убывания).
– Назовите число в котором цифра разряда
десятков на единицу больше цифры разряда единиц. (76).
– Что вы можете рассказать об этом числе? (Двузначное,
некруглое, сумма цифр 13, единиц – 6, десятков – 7,
предшествует число 75, последующее число 77).
4. Геометрический материал
Учитель. Хорошо. А теперь
геометрический материал.
Слайд 6
– Разделите все геометрические фигуры на две
группы. Фигуры с какими номерами входят в первую
группу? Во вторую группу?
– Что общего между фигурами каждой группы? (Есть
углы, нет углов).
– Назовите фигуры первой группы.
– Что вы помните о квадрате?
– Что вы помните о прямоугольнике?
5.
Учитель.Мышка довольна тем, как вы
быстро и правильно умеете считать и как много
знаете о числах и геометрических фигурах.
Слайд 7
6. Проверка индивидуальной работы
Учитель. А сейчас мы проверим ребят,
которые выполняли работу по карточкам.
Дети по очереди называют число и
соответствующую букву.
Слайд 8
III. Формулировка темы и целей урока
Учитель. Прочитайте тему нашего урока.
Какое слово вам знакомо? С помощью какого
арифметического действия находится сумма?
Значение какого вы еще не знаете? Сегодня мы
узнаем значение этого слова.
Слайд 9
– Посмотрите на доску. Что записано на ней? (Суммы).
– Какую сумму вычислить легче? (5 + 5) Чему равно
значение суммы?
– Можем ли мы сразу найти значение второй суммы? (Нет)
– Сегодня на уроке мы познакомимся с новым
действием, которое поможет нам легко и быстро
находить значение подобных выражений.
действие умножение и с результатом этого
действия – произведением. Мы познакомимся с
математическим знаком, который используется при
записи данного действия, попробуем решать задачи
с помощью умножения. Будем развивать
вычислительные навыки, память. Вы должны быть
внимательны и аккуратны.
IV. Создание проблемной ситуации
Учитель. Смайлик приготовил для вас
следующее задание.
Слайд 10
– Из следующих сумм назови только ту, в которой
все слагаемые одинаковые.
1 + 1 + 1 + 2
5 + 5 + 5 + 5 + 5 + 5
3 + 2 + 3 + 2
1 + 2 + 3 + 4 + 5
– Чему равно каждое слагаемое в сумме?
– Сколько раз повторяется слагаемое?
– Можем ли мы данное выражение записать
по-другому? (Пока не можем.)
Учитель. Мышка поможет нам в этом.
V. Изучение нового
Учитель.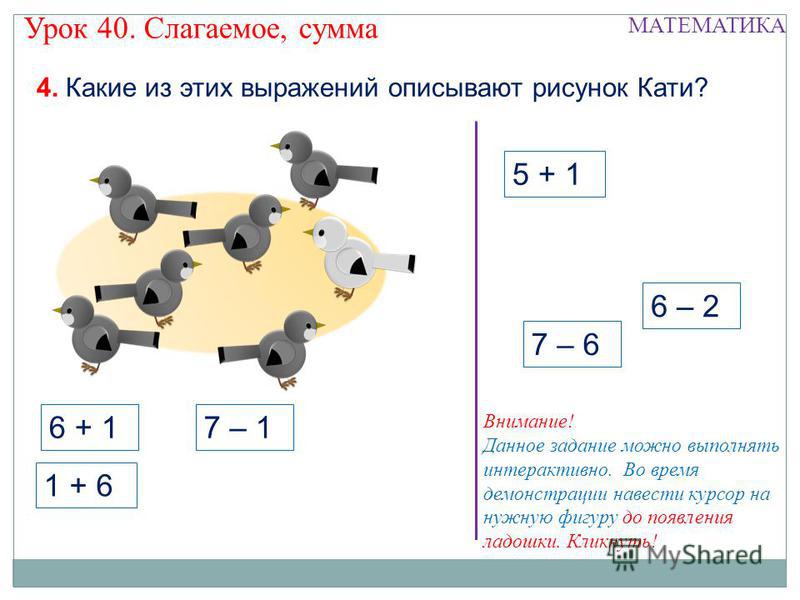
одинаковых слагаемых можно записать по-другому
– в виде ПРОИЗВЕДЕНИЯ.
5 + 5 + 5 + 5 + 5 + 5 = 5 • 6
– Для обозначения произведения используется
специальный знак в виде точки. Данное действие
называется действием умножения.
– Запись читается так: ПРОИЗВЕДЕНИЕ ЧИСЕЛ 5 И
6. (Повторить хором).
– Число 5 в произведении показывает, какое
слагаемое повторяется, и записывается на первом
месте. Число 6 показывает сколько раз оно
повторяется, записывается на втором месте.
– Откройте учебники на странице 91. Прочитайте
правило самостоятельно, постарайтесь запомнить
чтобы потом ответить на мои вопросы.
– Как можно записать сумму, состоящую из
одинаковых слагаемых?
– Скажите, что показывает число 5 в произведении?
На каком месте пишется?
– Что показывает число 6 в произведении? На каком
месте пишется?
Учитель.
правильность своих ответов.
Слайд 11
– Кто ответил так же, поднимите Смайлик.
– Вы были абсолютно правы.
VI. Закрепление
Игра «Помоги приземлиться летчику»
Учитель. Смайлик нашел ответ на свой
вопрос и предлагает вам игру.
Слайд 12
– Помоги приземлиться летчику.
– Найди для каждой суммы своё произведение,
прочитай правильно.
– Называем устно, проверяем на компьютере (2 + 2 +
2 произведение чисел 2 и 3)
– Я показываю сумму, вы находите произведение.
9 + 9 …
7 + 7 …
12 + 12 …
3 + 3 …
– Молодцы, вы хорошо справились с заданием.
Смайлик очень доволен. Кому было сложно,
поднимите Смайлика.
VII. Физминутка (Приложение
3)
Учитель. Вы хорошо потрудились, а
теперь отдохнём.
Попробуйте повторить движения за утенком.
Слайд 13
VIII. Закрепление
Учитель. Мы продолжаем свою работу.
Слайд 14
– Прочитайте произведения. Что обозначают
числа, образующие каждое произведение? (Первое
число показывает какое слагаемое использовали,
второе – сколько раз). Попробуйте заменить
суммой первое произведение.
– Мышка хочет проверить усвоение вами материала
и приготовила вам свое задание…
1. Работа в тетрадях
Учитель. Откройте тетради, запишите
число, классная работа. Прочитайте задание мышки.
Выполните его в тетрадях. Образец выполнения
перед вами. Выполните задание по образцу.
2. Самопроверка
Учитель. А теперь проверим выполнение
данной работы.
Слайд 15
– Кто выполнил задание безошибочно, поднимите
Смайлик.
– Кто сделал одну ошибку?
– Кто сделал 2 и более ошибок.
– Мышка говорит вам…
Слайд 16
4. Игра «Ёжики»
Учитель. Следующую игру вам
предлагает Смайлик.
Нужно подобрать к произведению сумму, вычислить
значение сумм. А потом мы сделаем вывод о том, как
связано значение суммы и соответствующего
произведения. (Произведение чисел 10 и 4 можно
заменить суммой 10 + 10 + 10 + 10, значение суммы равно
40)
– Кто не согласен, поднимите Смайлик.
Слайд 17
Вывод: Что вы можете сказать о
значении сумм и соответствующих произведений?
Значение сумм и соответствующих произведений
равны.
5. Задача
Учитель. Мышка любит решать разные
задачи. Одну из них она предлагает вам.
Слайд 18
– Прочитайте условие задачи.
– О чем говорится в задаче?
– Что известно?
– Что нужно найти?
– Какое действие будем использовать для
нахождения ответа задачи?
– Как сложение заменить умножением?
– Как будет звучать ответ задачи?
– Выполните задание мышки.
– Открыли тетради, записали слово задача. Не
записывая условия, пишем только решение и ответ.
В решении указываем, как найти ответ задачи при
помощи сложения, затем при помощи умножения, а
также находим значение выражения. И записываем
ответ задачи.
Слайд 19
6. Самопроверка
Учитель. Проверьте запись в тетрадях.
– Кто выполнил задание безошибочно, поднимите
Смайлик.
Слайд 20
– Мышка снова довольна вашей работой.
7. Веселые задачи
Учитель. Смайлик и Мышка довольны
вашей работой и у них есть для вас веселые задачи.
Сейчас мы решим некоторые из них.
Слайды 21-29
– Мы выбираем картинку. Слушаем задачу. Решаем
её сложением, а затем выполняем дополнительное
задание. Будьте внимательны.
Наша Маша рано встала,
Кукол всех она считала:
2 матрешки на окошке,
2 Аринки на перинке,
2 Танюшки на подушке.
Помоги нашей подружке
Посчитать её игрушки.
– Сколько кукол у Маши? Как нашли? Как сумму
заменить произведением?
Сбежала от Федоры посуда:
3 стакана, 3 чашки, 3 блюда.
Кто сосчитать готов,
Сколько всего беглецов?
У этого цветка 4 лепестка.
А сколько лепестков
У двух таких цветков?
Как-то раз в лесу густом,
Под березовым кустом,
Собрались грибы лесные,
Все красавцы удалые,
Ученик, ты не зевай
И грибы скорей считай.
5 груздей и 5 волнушек,
5 лисичек, 5 горькушек.
Кто ответить нам готов,
Сколько же всего грибов?
Насушила грибов
Белочка-хозяйка.
Справа – 6, слева – 6
Все пересчитай-ка.
3 зайчонка в час обеда
Захотели пообедать.
В огороде зайцы сели
И по семь морковок съели.
Кто считать, ребята, ловок
Сколько съедено морковок?
Какой шум и гам в лесу!
То кричат ребята.
И с испуга в 2 дупла
Спрятались бельчата.
Сколько маленьких бельчат
В дуплах проживает?
Там по 9 хвостиков
В темноте мелькают.
8. Кроссворд
– А теперь выполним задание Смайлика. Он стал
очень умным, многое узнал и хочет проверить вас.
Он предлагает вам решить кроссворд.
Каждый вопрос читает учитель. Дети отвечают.
Затем следует ответ – заполнение клеток.
- Как можно записать сумму одинаковых слагаемых? (В
виде произведения.) - Назовите арифметическое действие, результатом
которого является произведение? (Умножение.)
- Как выглядит знак, использующийся при записи
произведения? (Точка.) - В виде какого арифметического действия можно
представить произведение? (Сложения.)
– Посмотрите, в нашем кроссворде появилось еще
одно незнакомое слово. Прочитайте его. А вот что
обозначает это слово, мы узнаем на следующем
уроке математики.
– Подошел к завершению наш урок. Мышка и
Смайлик хотят проверить, что вы запомнили на
уроке.
Слайд 30
Учитель. А теперь мы проверим, как вы
усвоили материал урока. Откройте тетради на
печатной основе с. 39 найдите 2. Прочитайте
задание, выполните его самостоятельно в рабочих
тетрадях. Проверим устно.
– Кто согласен с ответом, поднимите Смайлик.
IX. Итог
– С какими новыми математическими терминами
познакомились на уроке? (Произведение,
умножение. )
– Какие слагаемые можно заменить произведением? (Одинаковые.)
– Как называется действие, результатом которого
является произведение? (Умножение.)
– Что вы можете сказать о значении произведения? (Равно
значению соответствующей суммы.)
X. Эмоциональный отклик
Учитель. А теперь я хочу узнать.
Понравился ли вам урок. На столах у вас есть
Смайлик, который помогал вам на уроке. Но у него
чего-то не хватает. Чего? Возьмите черный
фломастер или карандаш и нарисуйте Смайлику
ротик.
Слайд 31
– Если урок вам понравился, то улыбающийся.
Если нет, то грустный, как на экране.
– Покажите Смайликов. Я вижу, что урок вам
понравился. Вы тоже очень хорошо работали.
– Молодцы! Смайлик и Мышка считают, что за урок вы
заслужили оценку 5!
Слайд 32
– Урок окончен! Спасибо за урок!
Приложение 1
Приложение 2
Сумма (математика) — Википедия
У этого термина существуют и другие значения, см.
Су́мма (лат. summa — итог, общее количество) в математике — результат применения операции сложения величин (чисел, функций, векторов, матриц и т. д.), либо результат последовательного выполнения нескольких операций сложения (суммирования). Общими для всех случаев являются свойства коммутативности, ассоциативности, а также дистрибутивности по отношению к умножению (если для рассматриваемых величин умножение определено), то есть выполнение соотношений:
- a+b=b+a,{displaystyle a+b=b+a,}
- a+(b+c)=(a+b)+c,{displaystyle a+(b+c)=(a+b)+c,}
- (a+b)⋅c=a⋅c+b⋅c,{displaystyle (a+b)cdot c=acdot c+bcdot c,}
- c⋅(a+b)=c⋅a+c⋅b,{displaystyle ccdot (a+b)=ccdot a+ccdot b,}
В теории множеств суммой (или объединением) множеств называется множество, элементами которого являются все элементы объединяемых множеств, взятые без повторений.
Также сложение (нахождение суммы) может быть определено для более сложных алгебраических структур (сумма групп, сумма линейных пространств, сумма идеалов, и другие примеры).
Содержание
- 1 Сумма натуральных чисел
- 2 Алгебраическая сумма
- 2.1 Бесконечная сумма
- 2.2 Примеры последовательных сумм
- 2.3 Неопределённая сумма
- 2.4 «Дискретная» формула Ньютона — Лейбница
- 3 Этимология
- 4 Кодировка
- 5 См. также
- 6 Примечания
- 7 Литература
Сумма натуральных чиселПравить
Основная статья: Сложение (математика)
Пусть в множестве N{displaystyle mathbb {N} } находится a{displaystyle a} элементов, образующих подмножество A{displaystyle A} , и b{displaystyle b} элементов, образующих подмножество B{displaystyle B} (A⊂N,B⊂N{displaystyle Asubset mathbb {N} ,Bsubset mathbb {N} } , a и b — натуральные числа). Тогда арифметической суммой a+b{displaystyle a+b} будет количество элементов c{displaystyle c} , образующих подмножество C⊂N{displaystyle Csubset mathbb {N} } , полученное при дизъюнктном объединении двух исходных подмножеств C=A⊔B.
Итератор может быть выражением — тогда переменная оформляется со скобками как функция «f(){displaystyle f()} ». Например, сумма всех f(k){displaystyle f(k)} при натуральных числах k{displaystyle k} в определённом диапазоне:
- ∑0≤k<100f(k).{displaystyle sum _{0leq k<100}f(k).}
Сумма f(x){displaystyle f(x)} элементов x{displaystyle x} множества S{displaystyle S} :
- ∑x∈Sf(x).{displaystyle sum _{xmathop {in } S}f(x).}
Сумма μ(d){displaystyle mu (d)} всех положительных чисел d{displaystyle d} , являющихся делителями числа n{displaystyle n} :
- ∑d|nμ(d).{displaystyle sum _{d|n};mu (d).}
Под знаком итеративного суммирования может использоваться несколько индексов, например:
- ∑ℓ,ℓ′=∑ℓ∑ℓ′,{displaystyle sum _{ell ,ell ‘}=sum _{ell }sum _{ell ‘},}
причём набор из нескольких индексов можно сократить в виде так называемого мультииндекса.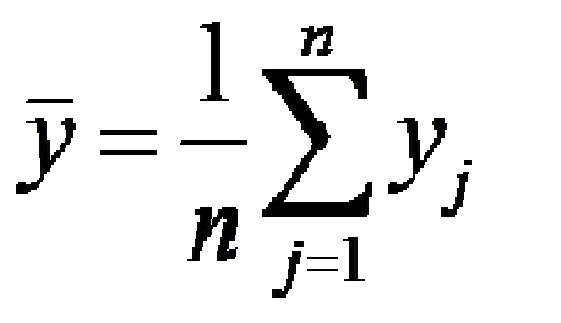
Латинское слово summa переводится как «главный пункт», «сущность», «итог». С XV века слово начинает употребляться в современном смысле, а также появляется глагол «суммировать» (1489 год).
Это слово проникло во многие современные языки: сумма в русском, sum в английском, somme во французском.
Специальный символ для обозначения суммы (Σ) первым ввёл Леонард Эйлер в 1755 году, его поддержал Лагранж, однако долгое время с этим символом конкурировал знак S. Окончательно обозначение Σ для суммы утвердили уже в XVIII веке Фурье и Якоби[2].
В Юникоде есть символ суммы U+2211 ∑ n-ary summation (HTML ∑ • ∑).
- Сложение
- Произведение
- ↑ Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren. Chapter 2: Sums // Concrete Mathematics: A Foundation for Computer Science (2nd Edition) (англ.
). — Addison-Wesley Professional, 1994. — ISBN 978-0201558029. (недоступная ссылка)
- ↑ Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. — 3-е изд. — СПб.: ЛКИ, 2008. — С. 175. — 248 с. — ISBN 978-5-382-00839-4.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — 7-е. — М.: Наука, 1969. — Т. 1. — 608 с. — 100 000 экз.
знак суммы в ворде как поставить
Как поставить знак суммы в ворде?
Знак суммы один из востребованных элементов в математике, часто он и используется в программе ворд, для написания разнообразных формул в ТЗ, курсовых.
В программе ворд, можно поставить пять видов знаков суммы, рассмотрим подробную инструкцию, как их можно поставить:
Первый шаг. Откроем новую книгу, на верхней панели выберем закладку «Вставка», в которой ищем блок с настройками (находиться в самом правом углу) «Символы» и нажимаем на иконку с надписью «Формула».
Второй шаг. Проваливаемся в это специальное меню, а в конструкторе формул находим иконку с подписью «Крупный оператор» и нажимаем на него. После чего на экране появиться выбор знаков суммы.
Для данного примера, я выбрал второй знак суммы, а вы можете поставить тот, который подходить для решения вашей конкретной задачи.
Ставим знак суммы в MS Word
Как вы наверняка уже знаете, в Microsoft Word есть довольно-таки большой набор специальных знаков и символов, которые при необходимости можно добавить в документ через отдельное меню. О том, как это сделать, мы уже писали, и более подробно ознакомиться с данной темой вы можете в нашей статье.
Помимо всевозможных символов и знаков, в MS Word также можно вставлять различные уравнения и математические формулы, используя готовые шаблоны или создавая собственные. Об этом мы тоже писали ранее, а в данной статье хотим поговорить о том, что имеет отношение к каждой из вышеупомянутых тем: как вставить значок суммы в Ворде?
Действительно, когда необходимо добавить этот символ, становится непонятно, где его искать — в меню символов или в математических формулах.
Знак суммы — это математический знак, и в Ворде он расположен в разделе “Другие символы”, если точнее, в разделе “Математические операторы”. Итак, чтобы его добавить, выполните следующие действия:
1. Кликните в том месте, куда необходимо добавить знак суммы и перейдите во вкладку “Вставка”.
2. В группе “Символы” нажмите на кнопку “Символ”.
3. В окошке, которое появится после нажатия на кнопку, будут представлены некоторые символы, но знака суммы вы там не найдете (по крайней мере, если ранее его не использовали). Выберите раздел “Другие символы”.
4. В диалоговом окне “Символ”, которое перед вами появится, выберите из выпадающего меню набор “Математические операторы”.
5. Найдите среди открывшихся символов знак суммы и кликните по нему.
6. Нажмите “Вставить” и закройте диалоговое окно “Символ”, чтобы продолжить работу с документом.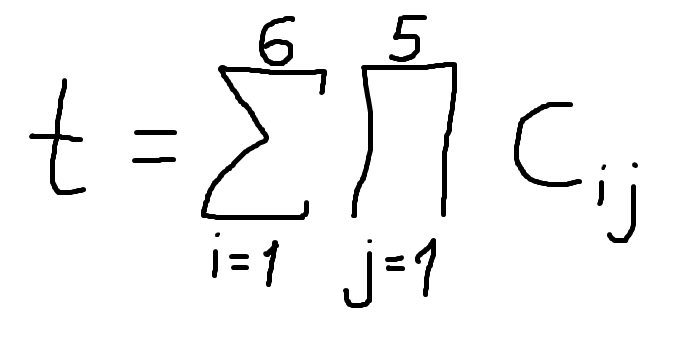
7. Знак суммы будет добавлен в документ.
Использование кода для быстрой вставки знака суммы
У каждого символа, расположенного в разделе “Символы”, есть свой код. Зная его, а также специальную комбинацию клавиш, вы можете добавлять любые символы, в том числе и значок суммы, значительно быстрее.
Узнать код знака можно в диалоговом окне “Символ”, для этого достаточно кликнуть по необходимому знаку.
Здесь же вы найдете комбинацию клавиш, которую необходимо использовать для преобразования числового кода в необходимый символ.
1. Кликните в том месте документа, где требуется поставить знак суммы.
2. Введите код “2211” без кавычек.
3. Не перемещая курсор с этого места, нажмите клавиши “ALT+X”.
4. Введенный вами код будет заменен на знак суммы.
Вот так просто можно добавить знак суммы в Ворде. В этом же диалоговом окне вы найдете огромное количество всевозможных символов и специальных знаков, удобно отсортированных по тематическим наборам.
Мы рады, что смогли помочь Вам в решении проблемы.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Как поставить знак суммы в Ворде?
Если знак суммы нужен не сам по себе, как греческая буква, а как элемент математической формулы суммирования, то простые способы не подойдут, надо будет честно вставлять формулу: Вставка — Объект — Формула (Insert — Object — Equation) для версия 2003 или Вставка — Формула (Insert — Equation) для более поздних версий. Там есть инструменты для создания полноценной формулы суммы, с обозначениями индекса суммирования и верхнего предела и с автоматической подгонкой знака суммы под размер общего члена суммируемого ряда.
Знак суммы в ворде
Сумма в математике обозначается греческой буквой «сигма».
Очень часто вверху и внизу сигмы пишутся границы суммирования (начальное и конечное значение), поэтому для вставки этого символа в документ Ворд правильнее всего использовать встроенный редактор формул.
1) Сначала откройте вкладку (панель инструментов) «Вставка» и нажмите на «Формула».
Другой способ вставить формулу — это комбинация клавиш «Alt» и «+».
2) Отобразится панель «Конструктор», на которой можно найти различные структуры.
В нашем случае нам будет нужна структура, которая называется «Крупный оператор».
3) Если щёлкнуть по этой структуре левой кнопкой мыши, то появится выпадающее меню, в котором будет несколько вариантов знака суммы.
Можно выбрать сумму как без границ суммирования, так и с границами суммирования.
4) Щёлкаем левой кнопкой мыши на нужной сумме, она отобразится в документе.
5) Теперь остаётся в специальных пунктирных квадратиках написать границы суммирования (если это нужно) и то, что суммируется.
Все, ну или почти все знаки математических действий, можно найти в Таблице символов. Если и тех не хватает можно пополнить с сайта производителя Ворда.
Открываем вкладку Символы и в таблице находим знак суммы, нажимаем его и вставляем.
Есть несколько способов поставить знак суммы — греческой буквы сигма.
- Не самый удобный, но работающий способ. Поскольку речь идет о греческой букве, то можно установить греческий алфавит и ввести букву просто с клавиатуры;
- Выбираем меню Вставка — Символ — Символы — Другие символы. В открывшемся окне ищем необходимый значок. Для этого стоит выбрать набор Математические операторы. Выбираем, копируем и вставляем — ∑.
- Нажимаем Пуск — Программы — Стандартные — Служебные — Таблица символов. Аналогично ищем там необходимый значок, нажимаем его, выбираем Копировать и вставляем в нужное место;
- Вводим с помощью Alt и цифр на дополнительной клавиатуре. Нажимаем и удерживаем Alt, набираем на клавиатуре код — 931;
- Вводим с помощью кода и Alt + X. Набираем кода — 2211. Затем, не перемещая курсом и находясь на английской раскладке клавиатуры, нажимаем Alt и удерживаем, а затем нажимаем X и отпускаем обе кнопки. Такой метод работает в программах Office, но редко — в браузерах.
- Вводим с помощью кода и Alt + X — способ 2. Набираем кода — 03A3. Затем, не перемещая курсом и находясь на английской раскладке клавиатуры, нажимаем Alt и удерживаем, а затем нажимаем X и отпускаем обе кнопки. Результат следующий — Σ. Как видите, он несколько отличается.
Для того, чтобы вставить знак суммы Σ в текстовом редакторе Microsoft word, существует 2 способа:
- Надо пойти по панелям: Вставка — Символ — Другие символы. Там есть знак суммы Σ, код знака — 2211. При использовании нового символа он попадает в категорию «Ранее используемые символы» в меню «Символ». Там тоже можно брать нужные символы.
- Нажать на: Пуск — Все программы — Стандартные — Служебные — Таблица символов. Выбрать знак суммы, его код: U+03A3. Затем нажать «Выбрать» и «Копировать». Далее нужно вставить его в нужную строку в тексте.
Знак суммы Σ — это большая буква «Сигма» в греческом алфавите (большие греческие буквы).
В программе Ворд есть несколько видов символов, которые обозначают «знак суммы».
А вот если знак суммы нужен для реально расчёта, то это уже другая история. Тогда обратился к формулам. Устанавливаем курсор в нужном месте при помощи мыши, ждём — Вставка — конструктор — выбираем формулу.
Обозначение суммирования
Обозначение суммирования
Часто математические формулы требуют добавления многих переменных Суммирование
или сигма-нотация — это удобная и простая форма сокращения, используемая для обозначения
краткое выражение для суммы значений переменной.
Пусть x 1 , x 2 , x 3 , …x n обозначают
набор из n чисел. x 1 — первое число в наборе.
представляет i-е число в наборе.
Обозначение суммирования включает:
Знак суммирования
Появляется в виде символа S, который является греческим
заглавная буква S. Знак суммирования S указывает нам суммировать элементы
последовательность. Появляется типичный элемент суммируемой последовательности.
справа от знака суммы.
Переменная суммирования, т.е. переменная, которая суммируется
Переменная суммирования представлена индексом, который помещается под
знак суммирования. Индекс часто обозначается буквой i. (Другие общие возможности
для представления индекса j и t.) Индекс появляется как выражение
i = 1. Индекс принимает значения, начиная со значения в правой части
уравнения и заканчивая значением над знаком суммы.
Начальная точка суммирования или нижняя граница суммирования
Точка остановки суммирования или верхний предел суммирования
Некоторые типичные примеры суммирования
| Это выражение означает суммирование значений x, начиная с в x 1 и заканчивая x n . |
| Это выражение означает суммирование значений x, начиная с в х 1 и заканчивая х 10 . |
| Это выражение означает сумму значений x, начиная с x 3 и заканчивающийся на х 10 . |
| Под пределами суммирования часто понимают i = от 1 до n. Тогда обозначения ниже и выше суммирования знак опущен. Следовательно, это выражение означает сумму значений х, начиная с х 1 и заканчивая x n . |
| Это выражение означает сумму квадратов значений x, начиная с x 1 и заканчивая x n .  |
Арифметические операции могут выполняться над переменными в рамках суммирования.
Например:
| Это выражение означает суммирование значений x, начиная с x 1 и заканчивая x n , а затем квадрат сумма. |
Арифметические операции могут выполняться над выражениями, содержащими более
чем одна переменная. Например:
| Это выражение означает форму продукта x умножается на y, начиная с x 1 и y 1 и окончание с x n и y n , а затем просуммируйте продукты. |
| В этом выражении с является константой, то есть элемент, который не включает в себя переменную суммирования и сумма включает n элементов.  |
Данные
Данные
и с, которое является константой = 11
|
3. |
Данные
|
и |
х i |
у я |
|
1 |
10 |
0 |
|
2 |
8 |
3 |
| 3 | 6 | 6 |
| 4 | 4 | 9 |
|
5 |
2 |
12 |
|
6. |
[Индекс]
Σ Символ суммы Sigma (копировать и вставить + знак суммы на клавиатуре)
Символ суммирования сигм известен большинству как математический символ, обозначающий сумму. Сигма Σ — один из самых популярных математических знаков, обозначающий сумму чего-либо. Нажмите на Символ сигмы ниже скопировать его в буфер обмена автоматически. Или посмотрите ниже, чтобы узнать, как набирать символ суммы с помощью клавиатуры, используя различные методы в зависимости от вашей системы.
| Математика | Σ | ∫ |
|---|---|---|
| ½ | π |
Текстовые символы
Что означает Sigma
Название сигмы, по одной из теорий, может продолжаться от финикийского Самеха. Согласно другой теории, его первоначальное название могло быть «Сан», тогда как «Сигма» было греческим нововведением, которое просто означало «шипение», основанное на номинализации глагола σίζω.
Sigma также используется для оператора суммирования, класса барионов в физике элементарных частиц, макроскопических сечений в физике ядра и элементарных частиц, собственной энергии в физике конденсированных сред, баланса классов счетов и общей суммы долгов и требований. в экономике набор символов, образующих алфавит, в лингвистике и информатике и т.д. Прочтите статью в Википедии о символе суммы, чтобы узнать больше о его значении.
Как ввести символ сигмы
Выберите свою систему и узнайте.
Окна
С клавиатуры
Альтернативные коды
Техника быстрого доступа, которая работает на настольных компьютерах и большинстве ноутбуков под управлением MS Windows.
| Альтернативный код | Символ |
|---|---|
| 0228 | Σ |
Состояния переключения
Настройте раскладку клавиатуры в Windows, чтобы вы могли вводить все дополнительные символы так же просто, как и любой другой текст. Настройка занимает около 5-10 минут, но вы будете печатать как босс.
С помощью этой техники вы можете назначить сигма-символ σ и любые другие текстовые символы на клавиатуру.
Карта символов
CharMap позволяет просматривать и использовать все символы и символы, доступные во всех шрифтах (некоторые примеры шрифтов: «Arial», «Times New Roman», «Webdings»), установленных на вашем компьютере.
Мак
Эмодзи на iOS (iPhone, iPad и iPod touch)
Текстовые символы с клавиатурой эмодзи iPhone 📲Простой и красивый способ узнать, как добавить виртуальную клавиатуру для символов эмодзи, видимых в виде маленьких картинок. Сама клавиатура предустановлена на вашем устройстве iOS, поэтому вам не нужно ничего скачивать или покупать.
Средство просмотра клавиатуры
Вы можете создавать часто используемые технические непричудливые символы, такие как «√ ∑ π ∞ ∆ ™ © æ £ ¢» и буквы с диакритическими знаками на Mac, используя клавишу [Option]. Я составил список горячих клавиш в своей статье и объяснил, как открыть программу просмотра клавиатуры. Вы также можете использовать средство просмотра клавиатуры в качестве альтернативы моему списку.
[Опция] + [W] дает знак сигма Σ.
Палитра персонажей
Палитра символов позволяет просматривать и использовать все буквы и символы, включая сигму, доступные во всех шрифтах (некоторые примеры шрифтов: «Arial», «Times New Roman», «Webdings»), установленных на вашем компьютере.
линукс
С клавиатуры
На самом деле существует 3 разных способа ввода символов в Linux с помощью клавиатуры. И все они могут создавать текстовый символ сигмы.
Карта символов
Карта символов позволяет просматривать и использовать все символы и символы, доступные во всех шрифтах (некоторые примеры шрифтов: «Arial», «Times New Roman», «Webdings»), установленных на вашем компьютере. Это также может помочь вам найти коды Unicode для ввода символов с клавиатуры.
HTML-код
Ниже приведен список объектов HTML и JavaScript для символа сигма. В Javascript вы должны писать как = «этот символ u2669», если вы хотите включить специальный символ в строку.
| HTML-объект | JS-сущность | Символ |
|---|---|---|
| &Сигма; | u03A3 | Σ |
Суммирование и обозначение произведения
Суммирование и обозначение произведения
Университет штата Иллинойс, математический факультет
MAT 305: Темы комбинаторики для K-8
Учителя
|
Суммирование и обозначение произведения |
|
| Обозначение суммирования | Обозначение продукта |
В этой заметке о содержании мы обсуждаем и иллюстрируем компактные
математические обозначения для выражения определенных типов сумм и
товары.
Обозначение суммирования
Временами, когда мы складываем, есть шаблон, по которому мы можем выразить
дополнения. Например, в сумме
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 +
10
наименьшее сложение равно 1, каждое последующее сложение на единицу больше
чем предыдущая, а самое большое слагаемое равно 10. Аналогично, в
сумма
2 + 6 + 10 + 14 + 18
наименьшее сложение равно 2, каждое последующее сложение на 4 больше, чем
предыдущее, а самое большое сложение — 18. Посмотрите, сможете ли вы
обнаруживать и описывать шаблоны слагаемых в следующих суммах.
| (1) |
3 + 6 + 9 + 12 + 15 + 18 + 21 |
| (2) |
5 + 10 + 20 + 40 + 80 + 160 |
| (3) |
2а + 4а + 6а + 8а + 10а + 12а + 14а |
| (4) |
1 + 4 + 9 + 16 + 25 + 36 + . . . . . |
| (5) |
3 + 6 + 9 + 12 + 15 + 18 + 21 + . . . |
| (6) |
10 — 16 + 22 — 28 + 34 — . . . |
Обозначение суммирования дает нам компактный способ представления
сложения в таких суммах. Вот, например, суммирование
обозначение для представления суммы первых 10 положительных целых чисел,
первая сумма, описанная на этой странице.
Приведенные ниже аннотированные символы обозначают важные элементы
используется в нотации суммирования (также называемой сигма-нотацией).
- Греческая буква сигма тесно связана с
слово «сумма». Буква сигма является сигналом того, что запись суммирования
используется. - Индекс суммирования , здесь буква i, является фиктивным
переменная, значение которой будет меняться при изменении слагаемых суммы.
Фиктивная переменная обычно появляется один или несколько раз в
выражение справа от греческой буквы сигма. - Нижний предел суммирования указывает наименьший
значение, которое примет индекс. Здесь наименьшее значение, которое я возьму
равно 1. Если не указано иное, мы увеличиваем это значение на 1
пока не достигнем верхнего предела суммирования. - Верхний предел суммирования указывает наибольший
значение, которое примет индекс. Здесь наибольшее значение я возьму
на 10. - Выражение справа от сигмы описывает или представляет
каждое слагаемое в терминах индексной переменной i. Вот, что
выражение — это просто индексная переменная. Часто гораздо больше
чем это.
Чтобы расширить это обозначение суммирования, то есть определить множество
слагаемых, которые мы должны суммировать, мы заменяем любое появление фиктивного
переменная в представлении слагаемого с нижним пределом
индексная переменная.
первое дополнение. Повторяем этот процесс со следующим значением индекса
переменной, используя это конкретное значение для переменной индекса в
добавление представления и упрощение по желанию или необходимости.
процесс замены и упрощения продолжается до тех пор, пока не будет достигнуто последнее значение индекса.
использоваться является верхним пределом суммирования.
Определите расширение этого обозначения суммирования:
Каждое слагаемое в сумме будет квадратом значения индекса.
значения индекса начинаются с 3 и увеличиваются на 1, пока не достигнут 7. Таким образом,
у нас есть значения индекса 3, 4, 5, 6 и 7, и квадраты этих
равны 9, 16, 25, 36 и 49. Таким образом, приведенные выше обозначения суммирования
представляет собой сумму 9 + 16 + 25 + 36 + 49.
В некоторых случаях мы можем не определить верхний предел суммирования
с определенным значением вместо использования переменной. Вот
пример.
Нижний предел суммирования равен 0, а верхний предел равен n.
слагаемое в сумме находится путем умножения значения индекса на 3 и
затем добавить 1 к этому. Когда j=0, сложение равно (3)(0)+1=1. Когда j=1,
сложение (3)(1)+1=4. Когда мы достигаем верхнего предела, слагаемое
равно (3)(n)+1. Поскольку мы не знаем конкретного значения n, мы используем
многоточие (…), чтобы сигнализировать о том, что шаблон сложения продолжается.
Вот расширение этой нотации суммирования. 93=27 и так далее. Последнего сложения нет, потому что верхний
предел суммирования равен бесконечности, что указывает на то, что мы просто продолжаем
создайте дополнения, следуя показанному шаблону. Вот расширение для
это бесконечное суммирование.
Обозначение продукта
Как только вы научитесь использовать нотацию суммирования для выражения
закономерности в суммах, нотация произведения имеет много сходных элементов, которые
сделать его простым, чтобы научиться использовать. Единственная разница в том, что
мы используем нотацию продукта, чтобы выразить закономерности в продуктах, то есть
когда факторы в продукте могут быть представлены некоторым шаблоном.
Вместо греческой буквы сигма мы используем греческую букву пи. Здесь
это обозначение произведения для представления произведения первых нескольких
квадратов:
| Учебный план |
Оценки и Оценка |
Контент Примечания |
Сессия Очертания |
Задания и Наборы задач |
Тесты и Викторины |
Исчисление I — Обозначение суммирования
Показать мобильное уведомление
Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т.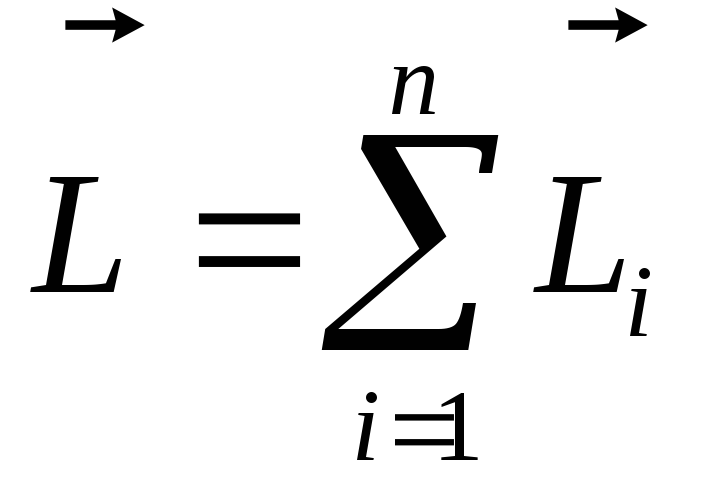
Раздел 7-8: Обозначение суммирования
В этом разделе нам нужно сделать краткий обзор нотации суммирования или сигма-нотации. Мы начнем с двух целых чисел, (n) и (m), где (n < m) и списка чисел, обозначенных следующим образом:
[{a_n},,,{a_{n + 1}},,,{a_{n + 2}},,, ldots ,,,{a_{m — 2} },,,{a_{m — 1}},,,{a_m}]
Мы хотим сложить их, другими словами, мы хотим,
[{a_n} + ,{a_{n + 1}} + ,,{a_{n + 2}} + ,, ldots + ,,{a_{m — 2}} + ,,{a_{m — 1}} + ,,{a_m}]
92}} & = 9 влево ( {100} вправо) — 12 влево ( { frac {{100 влево ( {101} вправо)}} {2}} вправо) + 4 влево ( { frac{{100left( {101} right)left( {201} right)}}{6}} right)\ & = 1293700end{align*}]
Выполнение этого вручную определенно заняло бы некоторое время, и есть большая вероятность, что мы могли бы сделать небольшую ошибку где-то на линии.
Как использовать суммирование (∑) в LaTeX?
LaTeX предоставляет нам значение по умолчанию или amsmath , который дает нам команды для красивого набора сумм. В этой статье мы рассмотрим различные команды для набора сумм с многочисленными примерами.
В математике суммирование обозначается заглавной греческой буквой сигма (∑). Команда для отображения знака суммы sum и Sigma . Хотя Sigma и sum возвращают один и тот же тип символа. В случае Sigma размер символа небольшой, но в случае sum размер символа и размер выражения настраиваются. 9{n}x_k = x_1 + x_2 + cdots + x_{n-1} + x_n
]
end{document}
Вывод:
Знак суммирования вместе с пределами отображаются по-разному в встроенном режиме и режиме отображения. Во встроенном режиме пределы отображаются рядом с символом, а в режиме отображения пределы отображаются ниже и выше знака суммирования.
hline
end{табличный}
конец{центр}
конец{документ} 9{i+j+k}}=?;mathit{if}|mathit{a}|>1
$$
end{document}
Вывод:
Используйте два или несколько нижних индексов под суммой
1. поверх : Эта команда позволяет вам написать две строки под обозначением суммы. Например:
documentclass{статья}
начать{документ}
[ sum_{ 1 leq i leq n поверх 1 leq j leq n }x_{i,j}]
end{document}
Вывод:
2. substack{аргумент} : Эта команда позволяет вам записать несколько строк в нотации суммы, взяв строки в качестве аргументов и разбив их с помощью команды новой строки \.
Например:
documentclass{статья}
usepackage{аммат}
начать{документ}
[ sum_{substack{ 1 leq i leq n \ 1 leq j leq n \ 1 leq i leq j leq n\ cdots}} ]
end{document}
Вывод:
3.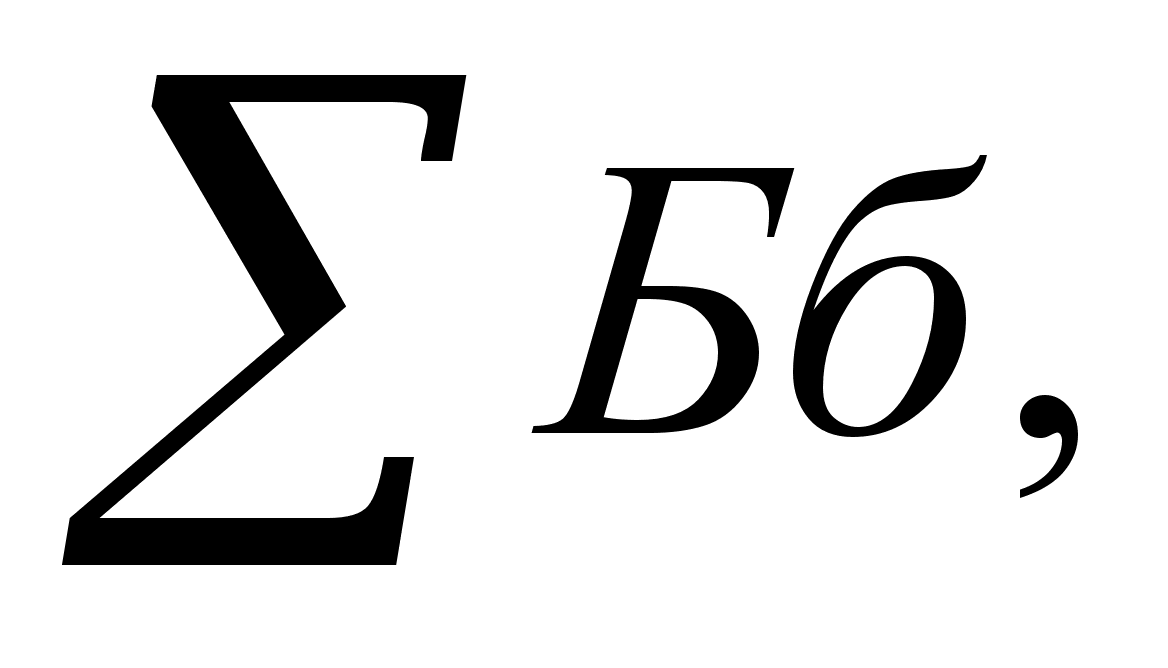
begin{subarray}{column_definition} cdots end{subarray} : Эта среда позволяет добиться того же эффекта, что и substack{argument} .
Например:
documentclass{статья}
usepackage{аммат}
начать{документ}
[ sum_{begin{подмассив}{c}
1 leq i leq n \
1 leq j leq n \
1 leq i leq j leq n\
cdots\
end{подмассив} } ]
end{document}
Вывод:
4. sideset{left}{right}{symbol} 9{sigma}}sum_{ 1 leq i leq n поверх 1 leq j leq n}x_{i,j}
]
добавление штриха к сумме
[
sideset{}{'}sum_{ 1 leq i leq n atop 1 leq j leq n }x_{i,j}
]
end{document}
Вывод:
Некоторые примеры
Как вы можете легко понять, символ суммы используется в следующих различных типах математических выражений.
documentclass{статья}
usepackage{amssymb}
начать{документ}
или все $ n in mathbb{N}^{ast} $ , имеем
[ sum_{k=1}^{n}k = frac{n(n+1)}{2}, quad sum_{k=1}^{n}k^2 = frac{n (n+1)(2n+1)}{6}, quad sum_{k=1}^{n}k^3 = left(frac{n(n+1)}{2}right )^2 ]
конец{документ} 9{n-j}a_{i+j,i}
]
end{document}
Вывод :
Заключение
Эта статья дает вам полное представление о том, как печатать суммирование в LaTeX, а также некоторые связанные команды.
Предстоящие учебные пособия
- Подчеркнуть
- Надпись
- Абзац Коробка
- Стол
- Пуля
- Выравнивание уравнения
- Новая команда
- Подзаголовок
- Пакет
- Использовать пакет
- Авторское право
- Рекомендация
Подписаться на учебные пособия
Распространенные математические символы и терминология
Математические символы и терминология могут сбивать с толку и создавать препятствия для изучения и понимания основ счета.
Эта страница дополняет наши страницы навыков счета и содержит краткий глоссарий общих математических символов и терминологии с краткими определениями.
Мы что-то упустили? Свяжитесь с нами, чтобы сообщить нам об этом.
Общие математические символы
+ Сложение, плюс, положительный
Символ сложения + обычно используется для обозначения того, что два или более числа должны быть сложены вместе, например, 2 + 2.
Символ + может также может использоваться для обозначения положительного числа, хотя это менее распространено, например, +2. Наша страница на Положительные и отрицательные числа объясняет, что число без знака считается положительным, поэтому плюс обычно не требуется.
Подробнее см. на нашей странице Дополнение .
− Вычитание, Минус, Отрицательное
Этот символ имеет два основных применения в математике:
- − используется, когда необходимо вычесть одно или несколько чисел, например, 2 − 2.
- Символ - также обычно используется для обозначения минуса или отрицательного числа, например -2.
Подробнее см. на нашей странице Вычитание .
× или * или . Умножение
Эти символы имеют одинаковое значение; обычно × используется для обозначения умножения, когда пишется от руки или используется на калькуляторе, например, 2 × 2.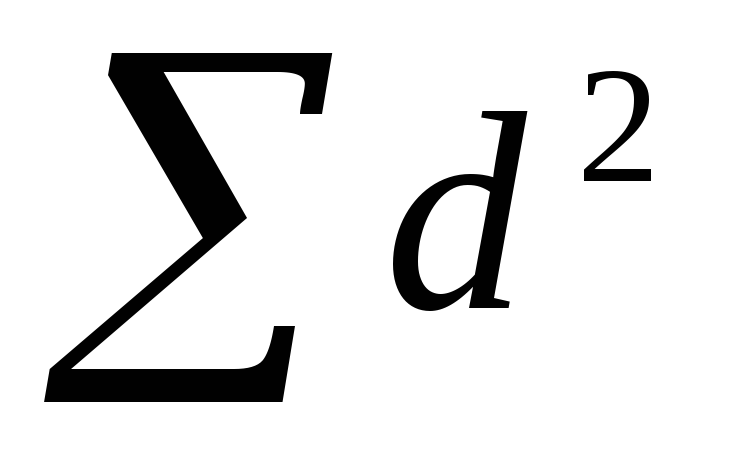
Символ * используется в электронных таблицах и других компьютерных приложениях для обозначения умножения, хотя в математике * имеет и другие, более сложные значения.
Реже умножение может обозначаться точкой . или вообще без символа. Например, если вы видите число, написанное вне скобок без оператора (символа или знака), то его следует умножить на содержимое скобок: 2(3+2) равно 2×(3+2).
Подробнее см. на нашей странице Умножение .
÷ или / Деление
Оба эти символа используются для обозначения деления в математике. ÷ обычно используется в рукописных вычислениях и на калькуляторах, например, 2 ÷ 2.
/ используется в электронных таблицах и других компьютерных приложениях.
Дополнительную информацию см. на нашей странице Division .
= равно
Символ = равно используется, чтобы показать, что значения по обе стороны от него одинаковы. Чаще всего он используется для отображения результата вычисления, например, 2 + 2 = 4, или в уравнениях, таких как 2 + 3 = 10 - 5,9.0021
Вы также можете встретить другие связанные символы, хотя они менее распространены:
- ≠ означает не равно. Например, 2 + 2 ≠ 5 - 2. В компьютерных приложениях (таких как Excel) символы <> означают не равно.
- ≡ означает идентично. Это похоже на equals, но не совсем то же самое. Поэтому, если сомневаетесь, придерживайтесь =.
- ≈ означает приблизительно равно или почти равно. Две стороны отношения, обозначенные этим символом, будут , а не быть достаточно точным для математической обработки.
< Меньше и > Больше
Этот символ < означает меньше, например, 2 < 4 означает, что 2 меньше 4.
Этот символ > означает больше, чем, например, 4 > 2
≤ ≥ Эти символы означают «меньше или равно» и «больше или равно» и обычно используются в алгебре. В компьютерных приложениях используются <= и >=.
≪ ≫ Эти символы менее распространены и означают намного меньше или намного больше.
± Плюс или минус
Этот символ ± означает «плюс или минус». Он используется для указания, например, доверительных интервалов вокруг числа.
Говорят, что ответ представляет собой «плюс-минус» другое число, или, другими словами, находится в диапазоне вокруг заданного ответа.
Например, 5 ± 2 на практике может быть любым числом от 3 до 7.
∑ Сумма
Символ ∑ означает сумму.
∑ — греческая заглавная сигма. Он обычно используется в алгебраических функциях, и вы также можете заметить его в Excel — значок кнопки «Автосумма» имеет сигму в качестве значка.
° Градусы
Градусы ° используются по-разному.
- Как мера поворота - угол между сторонами фигуры или поворот круга.
Круг равен 360°, а прямой угол равен 90°. Смотрите наш раздел на Геометрия подробнее.
- Измеритель температуры. Градус Цельсия или Цельсия используется в большинстве стран мира (за исключением США). Вода замерзает при 0°С, а кипит при 100°С. В США используется шкала Фаренгейта. По шкале Фаренгейта вода замерзает при 32°F и кипит при 212°F. См. нашу страницу: Системы измерения для получения дополнительной информации.
∠ Угол
Символ угла ∠ используется в качестве сокращения в геометрии (науке о формах) для описания угла.
Выражение ∠ABC используется для описания угла в точке B (между точками A и C). Точно так же ∠BAC будет использоваться для описания угла точки A (между точками B и C). Подробнее об углах и других геометрических терминах см. на наших страницах Геометрия .
√ Квадратный корень
√ — это символ квадратного корня.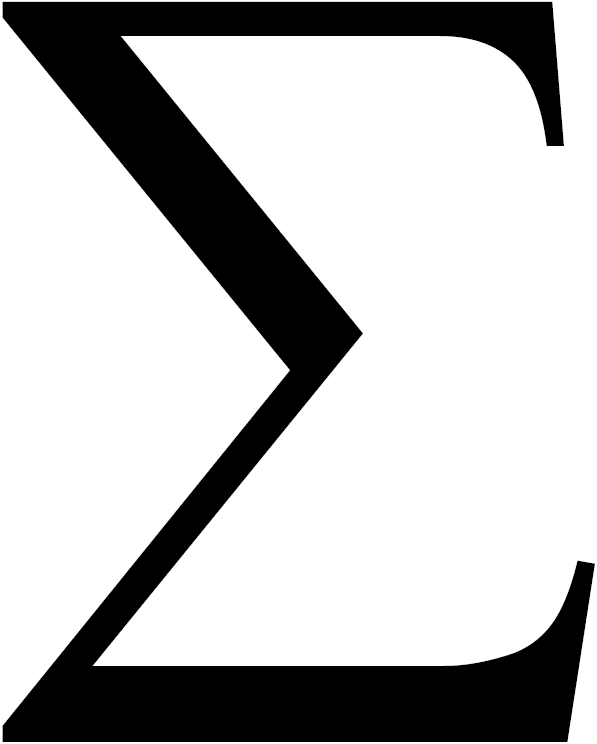
Например, квадратный корень из 4 равен 2, потому что 2 x 2 = 4. Квадратный корень из 9равно 3, потому что 3 x 3 = 9.
См. нашу страницу: Специальные числа и концепции , чтобы узнать больше о квадратных корнях.
n Степень
Целое число с надстрочным индексом (любое целое число n ) — это символ степени числа.
Например, 3 2 означает 3 в степени 2, что равно 3 в квадрате (3 x 3).
4 3 означает 4 в степени 3 или 4 в кубе, то есть 4 × 4 × 4.
См. наши страницы Вычисление площади и Вычисление объема , где приведены примеры использования чисел в квадрате и кубе .
Полномочия также используются для записи больших и малых чисел.
Большие числа
10 6 равно 1 000 000 (один миллион).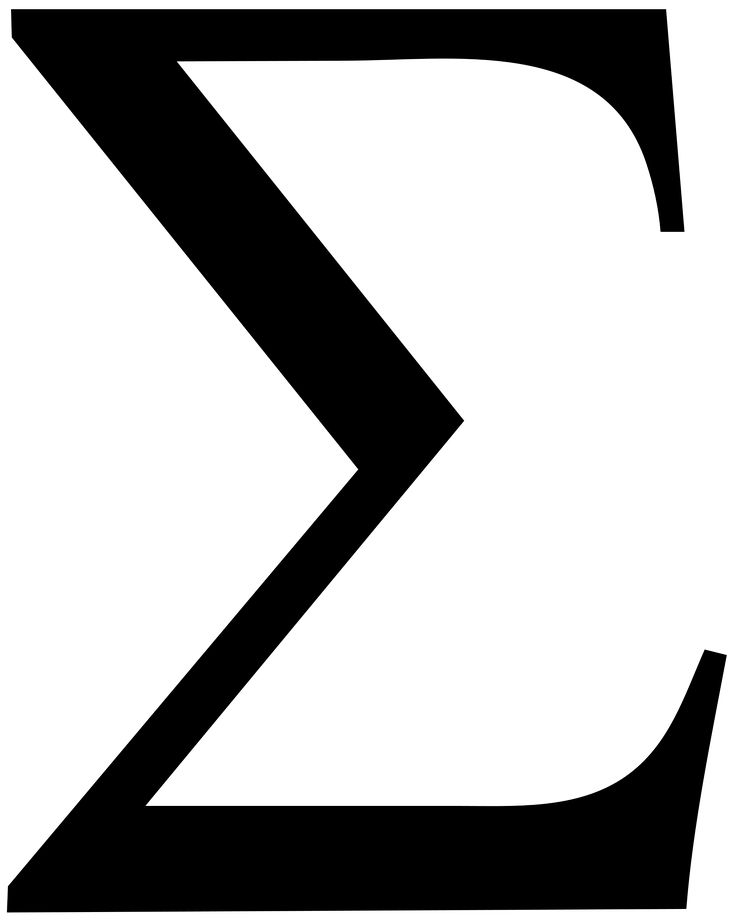
10 9 составляет 1 000 000 000 (один миллиард).
10 12 равно 1 000 000 000 000 (один триллион).
10 96 = 10 6 = 1 000 000 (один миллион).
. Десятичная точка
. — это десятичный символ точки, часто называемый просто «точкой». См. нашу страницу Decimals для примеров его использования.
, Разделитель тысяч
Запятая может использоваться для разделения больших чисел и облегчения их чтения.
Тысяча может быть записана как 1000, а также 1000, а миллион как 1000000 или 1000000. Запятая разбивает большие числа на блоки из трех цифр.
В большинстве англоязычных стран символ , не имеет никакой математической функции, он просто используется для облегчения чтения чисел.
В некоторых других странах, особенно в Европе, запятая может использоваться вместо десятичной точки, и действительно, десятичная точка может использоваться вместо запятой в качестве визуального разделителя.
[ ], ( ) Скобки, круглые скобки
Скобки ( ) используются для определения порядка вычислений в соответствии с правилом BODMAS.
Части расчета, заключенные в скобки, вычисляются первыми, например,
- 5 + 3 × 2 = 11
- (5 + 3) × 2 = 16
% Процент
Символ среднего символа %, или число из 100.
Изучите все около процентов на нашей странице: Введение в проценты
π PI
.
. греческий иероглиф для звука «п». Это часто встречается в математике и является математической константой. Пи — это длина окружности, деленная на ее диаметр, и имеет значение 3,14159.2653. Это иррациональное число, что означает, что его десятичные разряды продолжаются до бесконечности.

∞ Бесконечность
Символ ∞ означает бесконечность, понятие, что числа продолжаются вечно.
Каким бы большим ни было ваше число, вы всегда можете получить большее число, потому что вы всегда можете добавить к нему единицу.
Бесконечность — это не число, а идея чисел, продолжающихся вечно. Вы не можете добавить единицу к бесконечности, так же как вы не можете добавить единицу к человеку, любить или ненавидеть.
(bar x) (x-bar) Среднее
(bar x) является средним значением всех возможных значений x.
Этот символ чаще всего встречается в статистике.
Дополнительную информацию см. на нашей странице Averages .
! Факториал
! является символом факториала.
н! есть произведение (умножение) всех чисел от n до 1 включительно, т. е. n × (n−1) × (n−2) × … × 2 × 1,
Например:
5! = 5 × 4 × 3 × 2 × 1 = 120
10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3 628 800
| Труба
Труба '|' также упоминается как вертикальная полоса, vbar, пика и имеет множество применений в математике, физике и вычислительной технике.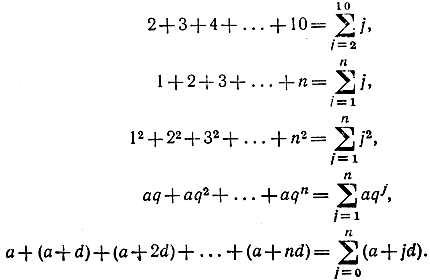
Чаще всего в базовой математике он используется для обозначения абсолютного значения или модуля действительного числа, где (vert x vert) является абсолютным значением или модулем (x) .
Математически это определяется как
$$vert x vert = biggl{begin{eqnarray} -x, x lt 0 \ x, x ge 0 end{eqnarray}$$
Проще говоря, (vert x vert) является неотрицательным значением (x). Например, модуль 6 равен 6, а модуль -6 также равен 6.
Он также используется в вероятности, где P(Z|Y) обозначает вероятность X при заданном Y.
∝ Пропорциональный
∝ означает «пропорционально » и используется, чтобы показать что-то, что изменяется по отношению к чему-то другому.
Например, если x = 2y, то x ∝ y.
∴ Поэтому
∴ — полезная сокращенная форма «следовательно», используемая в математике и естественных науках.
∵ Потому что
∵ — полезная сокращенная форма «потому что», не путать с «поэтому».
Математическая терминология (A-Z)
Амплитуда
Когда объект или точка движется циклически или подвергается вибрации или колебаниям (например, маятник), амплитуда - это максимальное расстояние, на которое он перемещается от своей центральной точки. См. введение в геометрию для получения дополнительной информации.
Апофема
Линия, соединяющая центр правильного многоугольника с одной из его сторон. Линия перпендикулярна (под прямым углом) к стороне.
Площадь
Геометрическая площадь определяется как пространство, занимаемое плоской формой или поверхностью объекта. Площадь измеряется в квадратных единицах, например, в квадратных метрах (м 2 ). Для получения дополнительной информации см. нашу страницу на площадь, площадь поверхности и объем .
Асимптота
Асимптота — это прямая линия или ось, которая конкретно связана с кривой линией. По мере того, как кривая линия простирается (стремится) к бесконечности, она приближается, но никогда не касается своей асимптоты (то есть расстояние между кривой и асимптотой стремится к нулю).
Ось
Линия отсчета, вокруг которой рисуется, вращается или измеряется объект, точка или линия. В симметричной форме ось обычно представляет собой линию симметрии.
Коэффициент
Коэффициент — это число или величина, умноженная на другую величину. Обычно он помещается перед переменной . В выражении 6 x 6 — коэффициент, а x — переменная.
Окружность
Окружность — это длина расстояния вокруг края круга. Это тип периметра , который уникален для круглых форм. Для получения дополнительной информации см. нашу страницу о изогнутых формах .
Данные
Данные представляют собой совокупность значений, информации или характеристик, которые часто имеют числовую природу. Их можно собрать с помощью научных экспериментов или других средств наблюдения. Они могут быть количественными или качественными переменными.
Диаметр
Диаметр — термин, используемый в геометрии для обозначения прямой линии, проходящей через центр круга или сферы и касающейся окружности или поверхности на обоих концах. Диаметр в два раза больше радиус .
Экстраполировать
Экстраполировать — это термин, используемый при анализе данных. Это относится к расширению графика, кривой или диапазона значений до диапазона, для которого не существует данных, с выводом значений неизвестных данных из тенденций в известных данных.
Фактор
Фактор — это число, которое мы умножаем на другое число. Множитель делится на другое число целое число раз. Большинство чисел имеют четное число множителей. Число в квадрате имеет нечетное количество делителей. А 9Простое число 0881 имеет два делителя — само себя и 1. Простой делитель — это делитель, который является простым числом.
Среднее, медиана и мода
среднее (среднее) набора данных вычисляется путем сложения всех чисел в наборе данных и последующего деления на количество значений в наборе. Когда набор данных упорядочен от наименьшего к наибольшему, медиана является средним значением. Мода — это число, которое встречается чаще всего.
Операция
Математическая операция — это шаг или этап вычисления или математическое «действие». К основным арифметическим действиям относятся сложение, вычитание, умножение и деление. Порядок, в котором выполняются операции при расчете, важен. Порядок операций известен как BODMAS .
Математические операции часто называют «суммами». Строго говоря, «сумма» — это операция сложения. В SYN мы говорим об операциях и вычислениях, но в повседневном языке часто можно услышать неверный общий термин «суммы».
Периметр
Периметр двумерной фигуры — это непрерывная линия (или длина линии), определяющая контур фигуры. Периметр круглой формы специально называется ее окружностью . Наша страница Периметр объясняет это более подробно.
Пропорция
Пропорция является относительным отношением. Отношения сравнивают одну часть с другой частью, а пропорции сравнивают одну часть с целым. Например, «3 из каждых 10 взрослых в Англии имеют избыточный вес». Пропорция связана с дроби .
Пифагор
Пифагор был греческим философом, которому приписывают ряд важных математических и научных открытий, возможно, самое значительное из которых стало известно как Теорема Пифагора .
Это важное правило применимо только к прямоугольным треугольникам. В нем говорится, что «квадрат гипотенузы равен сумме квадратов двух других сторон».
Количественный и качественный
Количественные данные — это числовые переменные или значения, которые могут быть выражены численно, т. е. сколько, сколько, как часто, и получены путем подсчета или измерения.
Качественные данные представляют собой переменные типа, которые не имеют числового значения и могут быть выражены описательно, т. е. с использованием имени или символа, и получены путем наблюдения.
Подробнее см. на нашей странице типов данных .
Радиан
Радиан — это единица измерения углов в системе СИ. Один радиан эквивалентен углу, образуемому в центре окружности дугой, длина которой равна радиусу. Один радиан чуть меньше 57,3 градуса. Полный оборот (360 градусов) составляет 2π радиан.
Радиус
Термин «радиус» используется в контексте кругов и других изогнутых форм. Это расстояние от центральной точки круга, сферы или дуги до их внешнего края, поверхности или окружности . Диаметр вдвое больше радиуса. Для получения дополнительной информации см. нашу страницу о изогнутых формах .
Диапазон
В статистике диапазон данного набора данных представляет собой разницу между наибольшим и наименьшим значениями.
Коэффициент
Соотношение — это математический термин, используемый для сравнения размера одной части с другой частью. Соотношения обычно отображаются в виде двух или более чисел, разделенных двоеточием, например, 7:5, 1:8 или 5:2:1.
Стандартное отклонение
Стандартное отклонение набора данных измеряет, насколько данные отличаются от среднего значения, т. е. это мера вариации или разброса набора значений. Там, где разброс данных низкий и все значения близки к среднему, стандартное отклонение будет низким. Высокое стандартное отклонение указывает на то, что данные разбросаны по более широкому диапазону
Термин
Термин — это отдельное математическое выражение. Это может быть одно число, одна переменная (например, x ) или несколько констант и переменных, перемноженных вместе (например, 3 x 2). Члены обычно разделяются операциями сложения или вычитания. Термин может включать операции сложения или вычитания, но только в скобках, например.
Переменная
Переменная фактор в математическом выражении, арифметическом соотношении или научном эксперименте, который может быть изменен. Эксперимент обычно имеет три типа переменных: независимые, зависимые и контролируемые. В выражении 6 x , 6 - это коэффициент , и x - это переменная.
Дисперсия
Дисперсия — это статистическое измерение, указывающее разброс между элементами в наборе данных. Он измеряет, насколько далеко каждый элемент в наборе от среднего и, следовательно, от каждого другого члена в наборе.
Вектор
Векторы описывают математические величины, которые имеют как величину, так и направление. Векторы встречаются во многих математических и физических приложениях, например. изучение движения, где скорость, ускорение, сила, перемещение и импульс являются векторными величинами.
Объем
Объем — это трехмерное пространство, занимаемое твердой или полой формой.
No related posts.
Как легко понять знаки Σ и П с помощью программирования
Для тех, кто подзабыл матешу
Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.
Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.
Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.
Знак Σ — сумма
Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:
Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.
На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:
- Взять все числа от 5 до 15 (снизу и сверху знака Σ).
- С каждым из этих чисел сделать то, что написано справа от Σ, — то есть умножить на два.
- Сложить результаты этих операций.
Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».
Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:
Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Что дальше
Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.
Как найти сумму числового и функционального ряда
Числовой ряд является некой последовательностью, которая рассматривается совместно с другой последовательностью (ее еще называют последовательностью частичных сумм). Подобные понятия применяются в математическом и комплексном анализе.
Сумму числового ряда можно легко вычислить в Excel с помощью функции РЯД.СУММ. Рассмотрим на примере, как работает данная функция, а после построим график функций. Научимся применять числовой ряд на практике при подсчете роста капитала. Но для начала немного теории.
Сумма числового ряда
Числовой ряд можно рассматривать как систему приближений к числам. Для его обозначения применяют формулу:
Здесь показана начальная последовательность чисел ряда и правило суммирования:
- ∑ — математический знак суммы;
- ai — общий аргумент;
- i — переменная, правило для изменения каждого последующего аргумента;
- ∞ — знак бесконечности, «предел», до которого проводится суммирование.
Запись 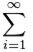
В соответствии с переменной i ряд можно записать развернуто:
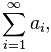
Определение суммы числового ряда дается через «частичные суммы». В математике они обозначаются Sn. Распишем наш числовой ряд в виде частичных сумм:
Сумма числового ряда – это предел частичных сумм Sn. Если предел конечен, говорят о «сходящемся» ряде. Бесконечен – о «расходящемся».
Сначала найдем сумму числового ряда:
Теперь построим в Excel таблицу значений членов ряда:
Общий первый аргумент берем из формулы: i=3.
Все следующие значения i находим по формуле: =B4+$B$1. Ставим курсор в нижний правый угол ячейки В5 и размножаем формулу.
Найдем значения. Делаем активной ячейку С4 и вводим формулу: =СУММ(2*B4+1). Копируем ячейку С4 на заданный диапазон.
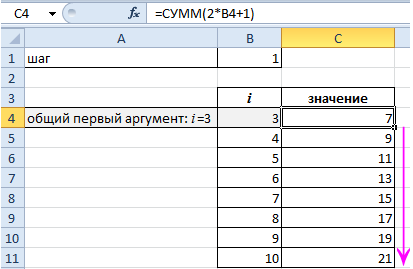
Значение суммы аргументов получаем с помощью функции: =СУММ(C4:C11). Комбинация горячих клавиш ALT+«+» (плюс на клавиатуре).
Функция РЯД.СУММ в Excel
Для нахождения суммы числового ряда в Excel применяется математическая функция РЯД.СУММ. Программой используется следующая формула:
- х – значение переменной;
- n – степень для первого аргумента;
- m – шаг, на который увеличивается степень для каждого последующего члена;
- а – коэффициенты при соответствующих степенях х.
Важные условия для работоспособности функции:
- все аргументы обязательные (то есть все должны быть заполнены);
- все аргументы – ЧИСЛОвые значения;
- вектор коэффициентов имеет фиксированную длину (предел в «бесконечность» не подойдет);
- количество «коэффициентов» = числу аргументов.
Вычисление суммы ряда в Excel
Та же функция РЯД.СУММ работает со степенными рядами (одним из вариантов функциональных рядов). В отличие от числовых, их аргументы являются функциями.
Функциональные ряды часто используются в финансово-экономической сфере. Можно сказать, это их прикладная область.
Например, положили в банк определенную сумму денег (а) на определенный период (n). Имеем ежегодную выплату х процентов. Для расчета наращенной суммы на конец первого периода используется формула:
На конец второго и последующих периодов – вид выражений следующий:
S2 = a (1 + x) 2 ; S3 = a (1 + x) 2 и т.д.
Чтобы найти общую сумму:
Sn = a (1 + x) + a (1 + x) 2 + a (1 + x) 3 + … + a (1 + x) n
Частичные суммы в Excel можно найти с помощью функции БС().
Исходные параметры для учебной задачи:
Используя стандартную математическую функцию, найдем накопленную сумму в конце срока сумму. Для этого в ячейке D2 используем формулу: =B2*СТЕПЕНЬ(1+B3;4)
Теперь в ячейке D3 решим эту же задачу с помощью встроенной функции Excel: =БС(B3;B1;;-B2)
Результаты одинаковые, как и должно быть.
Как заполнить аргументы функции БС():
- «Ставка» — процентная ставка, под которую оформлен вклад. Так как в ячейке В3 установлен процентный формат, мы в поле аргумента просто указали ссылку на эту ячейку. Если было бы указано число, то прописывали бы его сотую долю (20/100).
- «Кпер» — число периодов для выплат процентов. В нашем примере – 4 года.
- «Плт» — периодические выплаты. В нашем случае их нет. Поэтому поле аргумента не заполняем.
- «Пс» — «приведенная стоимость», сумма вклада. Так как мы на время расстаемся с этими деньгами, параметр указываем со знаком «-».
Таким образом, функция БС помогла найти нам сумму функционального ряда.
В Excel есть и другие встроенные функции для нахождения разных параметров. Обычно это функции для работы с инвестиционными проектами, ценными бумагами и амортизационными платежами.
Построение графика функций суммы числового ряда
Построим график функций, отражающий рост капитала. Для этого нам нужно построить график функции являющейся суммой построенного ряда. За пример, возьмем те же данные по вкладу:
Дальше нам нужна функция для начисления сложных процентов — БС(). Мы узнаем будущею стоимость инвестиций при условии равных платежей и постоянной процентной ставке. Используя функцию БС(), заполним таблицу:
В первой строке показана накопленная сумма через год. Во второй – через два. И так далее.
Сделаем еще один столбец, в котором отразим прибыль:
Как мы считали – в строке формул.
На основании полученных данных построим график функций.
Выделим 2 диапазона: A5:A9 и C5:C9. Переходим на вкладку «Вставка» — инструмент «Диаграммы». Выбираем первый график:
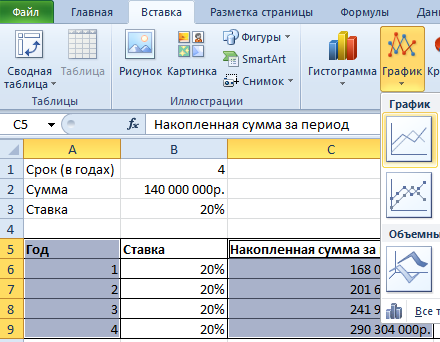
Сделаем задачу еще более «прикладной». В примере мы использовали сложные проценты. Они начисляются на наращенную в предыдущем периоде сумму.
Возьмем для сравнения простые проценты. Формула простых процентов в Excel: =$B$2*(1+A6*B6)
Добавим полученные значения в график «Рост капитала».
Какие именно выводы сделает инвестор – очевидно.
Математическая формула частичной суммы функционального ряда (с простыми процентами): Sn = a (1 + x*n), где а – первоначальная сумма вклада, х – проценты, n – период.
Сумма ряда
Содержание:
Понятие суммы ряда
Постановка задачи. Найти сумму ряда
где 
План решения. Суммой ряда 


где
1. По условию задачи
Если корни знаменателя различаются на целое число, т.е. 




По этой ссылке вы найдёте полный курс лекций по высшей математике:
2. Разлагаем общий член ряда на элементарные дроби:
и выписываем несколько членов ряда так, чтобы было видно, какие слагаемые сокращаются при вычислении частичных сумм ряда.
3. Находим 

сократив соответствующие слагаемые.
4. Вычисляем сумму ряда по формуле (1)
и записываем ответ.
Пример:
Найти сумму ряда
Решение:
1. Корни знаменателя 




2. Разлагаем общий член ряда на элементарные дроби
и выписываем несколько членов ряда:
3. Сокращая все слагаемые, какие возможно, находим 
4. Вычисляем сумму ряда по формуле (1):
Ответ:
Возможно вам будут полезны данные страницы:
Вычисление суммы ряда почленным интегрированием
Постановка задачи. Найти сумму функционального ряда вида
и указать область сходимости ряда к этой сумме.
План решения.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
Если 

2. Делаем в исходном ряде замену 
с областью сходимости 
3. Известна формула для вычисления суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке
, целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем
Заметим, что так как ряд (1) сходится в граничной точке 
6. Вычисляем интеграл, делаем замену 

Замечание. Если ряд имеет вид
то применяем теорему о почленном интегрировании степенного ряда дважды или разлагаем дробь на элементарные:
и вычисляем сумму каждого ряда почленным интегрированием.
Пример:
Найти сумму ряда
и указать область сходимости ряда к этой сумме.
Решение:
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
В граничных точках при 


Следовательно, данный ряд сходится при всех 
2. Сделаем замену 
3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке 
Заметим, что так как ряд (1) сходится в граничной точке 

6. Заменяя 

Ответ.
Вычисление суммы ряда почленным дифференцированием
Постановка задачи. Найти сумму функционального ряда вида
и указать область сходимости ряда к этой сумме.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
Если 

2. Делаем в исходном ряде замену 
Следовательно, достаточно найти суммы рядов

3. Известна формула для суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (1), получаем
6. Вычисляем производную и делаем замену 

Замечание. Если ряд имеет вид
то вычисляем сумму трех рядов, причем при вычислении суммы ряда
применяем теорему о почленном дифференцировании степенного ряда дважды.
Пример:
Найти сумму ряда
и указать область сходимости ряда к этой сумме.
Решение:
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством 



2. Делаем в исходном ряде замену 
Следовательно, достаточно найти суммы рядов
3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии:
Следовательно, 

4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (2), получаем
Заменяя 

Ответ.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
http://exceltable.com/funkcii-excel/nayti-summu-chislovogo-ryada
http://natalibrilenova.ru/summa-ryada/
‹— Назад
Символ суммирования
В математике для записи сумм, содержащих много слагаемых, или в случае, когда число слагаемых обозначено буквой, применяется следующая запись:
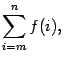
которая расшифровывается так
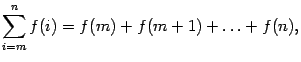 |
(14.1) |
где — функция целочисленного аргумента. Здесь символ
(большая греческая буква «сигма») означает суммирование. Запись
внизу символа суммирования показывает, что переменная, которая меняет свои значения от слагаемого к слагаемому, обозначена буквой
и что начальное значение этой переменной равно
. Запись вверху обозначает последнее значение, которое принимает переменная
.
Пример 14.2 Вычислим несколько сумм:
1) 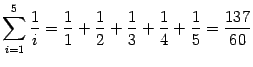
2) 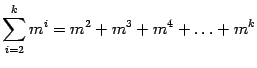
и знаменателем прогрессии равным
, то эту сумму легко найти
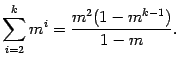
3) 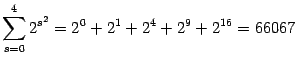
4) 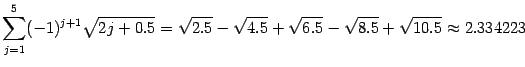
5) 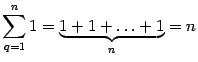
В курсе линейной алгебры чаще всего будут встречаться суммы вида . Здесь переменная с индексом рассматривается как функция от своего индекса. Поэтому
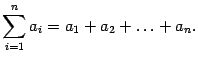
С помощью знака суммы формулу (10.1) скалярного произведения векторов можно записать так:
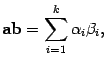 |
(14.2) |
где для трехмерного пространства , для плоскости
.
Для единообразия будем считать, что
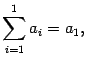
и говорить, что это сумма, содержащая одно слагаемое.
Замечание 14.1 Буква, стоящая внизу под знаком суммы (индекс суммирования), не влияет на результат суммирования. Важно лишь, как от этого индекса зависит суммируемая величина. Например,
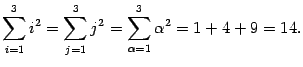
Или
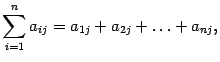
в правой части никакой буквы нет, значит, и результат от
не зависит.
Предложение 14.1 Множитель, не зависящий от индекса суммирования, может быть вынесен за знак суммы:
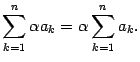
Доказательство этого предложения предоставляется читателю.
Предложение 14.2
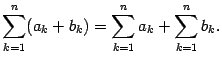 |
(14.3) |
Это предложение является частным случаем следующего утверждения.
Доказательство. Пусть
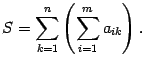
Тогда
Раскроем скобки в правой части этого равенства. Получим сумму элементов при всех допустимых значениях индексов суммирования. Слагаемые сгруппируем по-другому, а именно, сначала соберем все слагаемые, у которых первый индекс равен 1, потом, у которых первый индекс равен 2 и т.д. Получим
Заменив в этом равенстве в левой части его выражением через знаки суммирования, получим формулу (14.4).
Замечание 14.2 Двойные суммы из равенства (14.4) можно записывать и без использования скобок
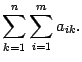
Нужно помнить, что двойная сумма означает сумму элементов для всех допустимых значений индексов суммирования. По этой же причине, если встречается запись, содержащая подряд три или более символов суммирования, то порядок расстановки этих символов можно менять произвольно.
Если границы изменения всех индексов суммирования одинаковы, то можно для суммирования по нескольким индексам использовать запись вида
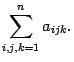
Иногда под символом суммы указывают дополнительные условия, налагаемые на индексы суммирования. Так запись
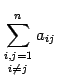
означает, что в сумму не включаются величины ,
,…,
, то есть
с равными индексами.
Иногда в записи суммы не указываются границы изменения индексов, например,
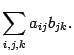
Такая запись используется, когда значения, которые могут принимать индексы, очевидны из предыдущего текста или будут оговорены сразу после окончания формулы.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
7.1. Свойства знака суммирования
Рассмотрим сумму
вида
.
В математике
принято следующее обозначение системы
.
Выражение ai,
стоящее под знаком ,
называется общим членом суммы. Под
знаком
записывается индекс суммирования i
и его начальное значение k,
а над знаком
– последнее значение i,
равное n.
Выражение
означает,
что в общем числе суммы надо последовательно
задаватьи получившиеся числа сложить.
Примеры:
1. Обозначение
индекса суммирования может быть изменено,
т.е.
.
2. Множитель, не
зависящий от индекса суммирования,
можно вынести за знак суммы
,
где
не зависит от
.
3.
.
Нередко знак
приходится употреблять несколько раз.
Рассмотрим, например, сумму всех элементов
матрицы
:
.
4. Два знака суммы
могут быть переставлены местами

При суммировании
по разным индексам скобки обычно опускают
и вместо

,
подразумевая, что слагаемоесначала суммируют по
при фиксированном
(внутренняя сумма), затем полученные
величины суммируют по(внешняя сумма).
5. При суммировании
по двум индексам можно выносить из-под
знака внутренней суммы множитель, не
зависящий от индекса внутреннего
суммирования:
.
7.2. Понятие квадратичной формы
Квадратичной
формой
отn
неизвестных
называется сумма, каждое слагаемое
которой является квадратом одного из
этих неизвестных или произведением
двух разных неизвестных
Пример.
является квадратичной формой от трех
неизвестных.
Каждую квадратичную форму можно записать
в стандартном виде. Для этого сначала
приведем подобные в квадратичной форме,
затем обозначим коэффициент причерез
,
а коэффициент при произведениичерез
,
причем.
Члензапишем в виде
.
Теперь квадратичную форму можно записать
в виде:
Матрица
называется матрицей квадратичной формы
.
Так как,
то– симметричная матрица.
Пример.
Запишем предложенную (рассмотренную
выше) квадратичную форму в стандартном
виде и найдем матрицу.
Матрица
квадратичной формы имеет вид:

Квадратичная
форма может быть представлена в
векторно-матричном виде
,
.
Действительно:
=
,
здесь
– этоi–й
столбец матрицы
.
Приведенные
выкладки показывают в частности, что
если А –
симметричная матрица, то выражение
является квадратичной формой от
неизвестных.
Если
– произвольный
-мерный
вектор, то, подставляя в квадратичную
форму
вместо x,
получим число
,
которое называют значением квадратичной
формына вектор.
7.3. Канонический базис квадратичной формы
Базис
пространства
называется каноническим базисом
квадратичной формы,
еслипри
.
Если– канонический базис
,
то выражение
,
где
называется каноническим видом
в базисе
,
где– новый набор неизвестных.
Теорема.
Если
– разложение вектора
по каноническому базису
квадратичной формы
,
то значениена векторе
вычисляется по формуле
,
.
Доказательство:
рассмотрим следующую цепочку равенств
Доказанная теорема
утверждает, что если известен канонический
базис
квадратичной формы
и ее канонический вид в этом базисе, то
для вычисления значенияквадратичной формы
на векторе
достаточно:
1. Разложить
по каноническому базису
.
2. Коэффициенты
разложения
подставить вместо неизвестных
в канонический вид.
Квадратичная форма
имеет много разных канонических базисов.
Процесс построения канонического базиса
называется приведением квадратичной
формы к сумме квадратов.
Теорема.
Ортонормированный базис пространства
,
состоящий из собственных векторовсимметрической матрицы
,
,
где– множество всех собственных векторов
матрицыпорядка
,
принадлежащих ее собственным значениям,
является каноническим базисом квадратичной
формы,
а выражение– ее каноническим видом в базисе
.
Доказательство:
Убедимся сначала, что– канонический базис
.
Имеем,
если,
так какортонормированная система векторов.
Вычислим
теперь коэффициенты ее в каноническом
виде:,
так как система векторовнормированная, то
,
.
Итак, доказано,
что если
– ортонормированный базис из собственных
векторов симметрической матрицы,
то в этом базисе квадратичная формаимеет вид
,
где– собственные значения матрицы
.
Пример 1. Найти
канонический вид и канонический базис
квадратичной формы
в ортонормированном базисе из собственных
векторов матрицы

.
Собственные
значения матрицы:
,
,
.
Найдем,
,
.
Составим систему уравнений:

Решение имеет вид
,
=
.
Также находим
,
решая систему
и
нормируя решение
.
Решая уравнение
,
получаем
=
.
Заметим, что эти
векторы ортогональны, так как матрица
симметрическая.
В базисе
форма имеет вид
.
Рассмотрим еще
один метод построения канонического
базиса и канонического вида квадратичной
формы (метод Якоби). Будем говорить, что
матрица
удовлетворяет условию Якоби, если
определители

,
называемые
угловыми минорами матрицы
,
не равны 0. Заметим, что,
.
Обозначим черезматрицу
.
Из условия
следует, что
.
Следовательно, каждая система уравнений
,
где
–k-й
вектор диагональной системы, – имеет
единственное решение,
.
Система векторов
называется системой векторов Якоби
матрицы,
которая удовлетворяет условию Якоби.
Пример 2. Найти
систему векторов Якоби для формы, которая
рассматривалась в примере 1.
Сначала
убедимся, что матрица удовлетворяет
условию Якоби
;
,
Вектор
является решением системы уравнений
Единственное ее
решение – вектор
.
Вектор
является решением системы

Методом Гаусса
находим ее решение:
.
Наконец, вектор
является решением системы
Преобразуем
эту систему уравнений методом Гаусса
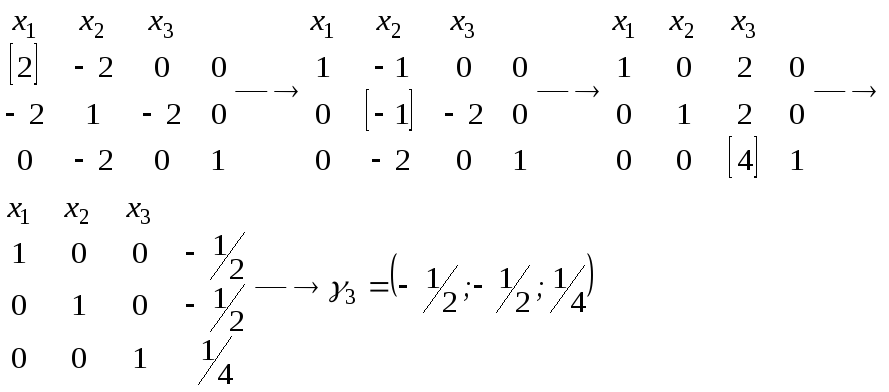
Если матрица
квадратичной формы
удовлетворяет условию Якоби, то система
векторов Якобиматрицы
является каноническим базисом квадратичной
формы,
а выражение
– ее
каноническим видом в базисе
.
Наша форма в базисе Якоби имеет вид.
Итак, в разных
канонических базисах квадратичная
форма имеет разный канонический вид,
однако, положительный индекс (число
положительных коэффициентов в каноническом
виде) и отрицательный индекс остаются
неизменными. У формы, рассмотренной в
примерах 1 и 2 положительный индекс равен
2, а отрицательный индекс равен 1.
Соседние файлы в папке Линейная и векторная алгебра
- #
- #
02.04.201584.68 Кб20лаба.xmcd
- #
02.04.201584.68 Кб22лаба1.xmcd
- #
02.04.2015205.1 Кб21лаба2.xmcd
- #
- #














 )
) ). — Addison-Wesley Professional, 1994. — ISBN 978-0201558029. (недоступная ссылка)
). — Addison-Wesley Professional, 1994. — ISBN 978-0201558029. (недоступная ссылка)





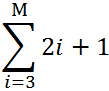
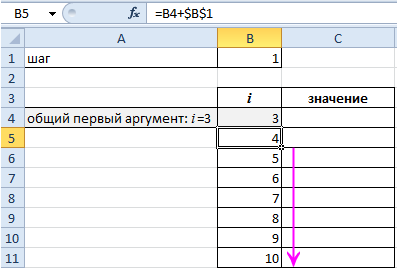
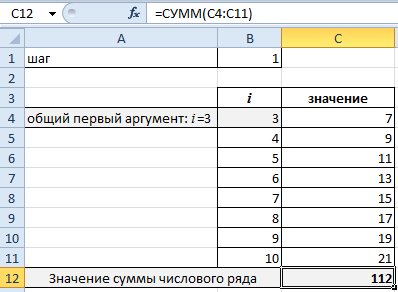
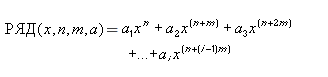
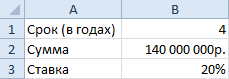
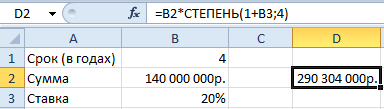
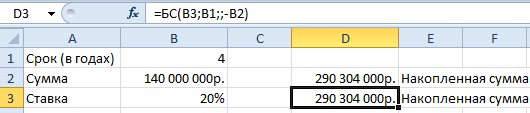
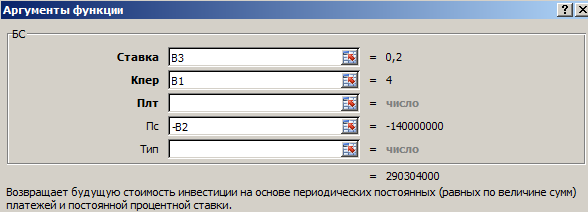
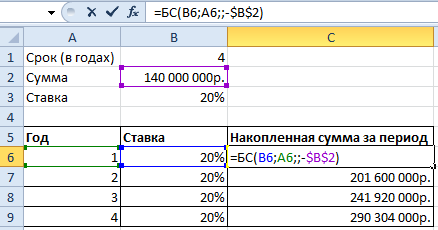
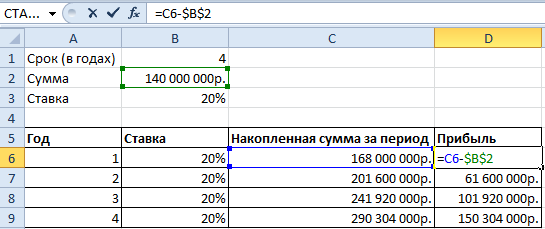
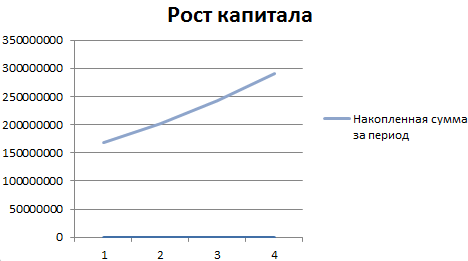
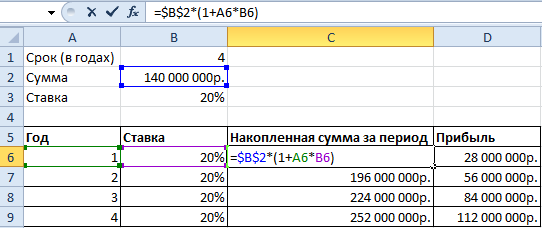
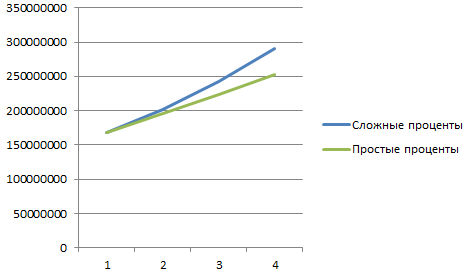




















 , целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем
, целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем