Слайд 1ГИА 2013
Модуль ГЕОМЕТРИЯ
№11
Автор презентации:
Гладунец Ирина Владимировна
учитель математики МБОУ гимназия №1
г.Лебедянь Липецкой области

Слайд 2Модуль «ГЕОМЕТРИЯ» №11
Ответ: 6.
Найти площадь треугольника.
В
С
А
8
3
30⁰

Слайд 3Повторение
Площадь треугольника равна половине произведения двух сторон на синус угла
между ними

Слайд 4Модуль «ГЕОМЕТРИЯ» №11
Ответ: 31,5.
Катет АС на 2 больше катета ВС.
Найти площадь треугольника
В
С
А
7
АС=ВС+2=7+2=9

Слайд 5Повторение
Площадь прямоугольного треугольника равна половине произведения катетов

Слайд 6Модуль «ГЕОМЕТРИЯ» №11
Ответ: .
Найти площадь треугольника
В
А
С
4

Слайд 7Повторение
Площадь треугольника равна половине произведения двух сторон на синус угла
между ними
Сумма квадратов синуса и косинуса одного и того же
угла равна единице

Слайд 8Модуль «ГЕОМЕТРИЯ» №11
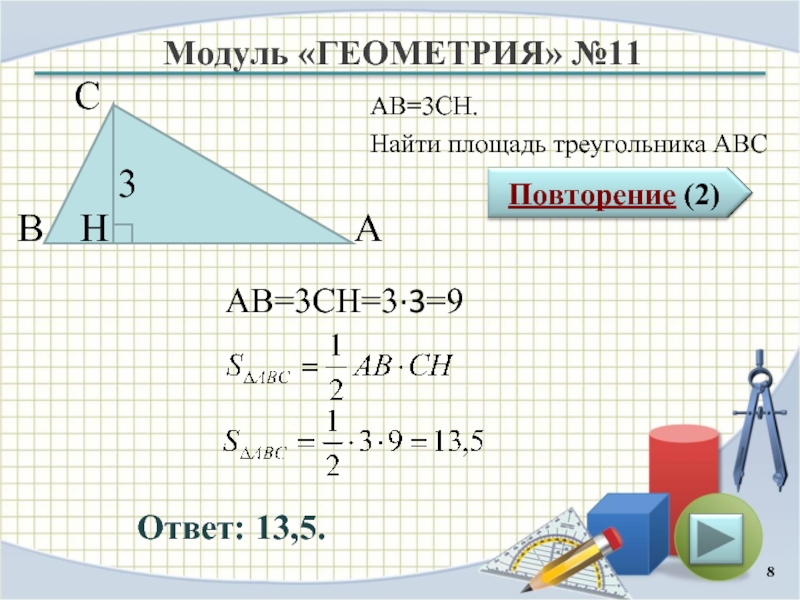
Ответ: 13,5.
АВ=3CH.
Найти площадь треугольника АВС
В
С
А
3
H
АВ=3CH=3∙3=9
Слайд 9Повторение
Высота треугольника – это отрезок, проведенный из вершины к противоположной
стороне под прямым углом
Площадь треугольника равна половине произведения основания на
высоту

Слайд 10Модуль «ГЕОМЕТРИЯ» №11
Ответ:1,5 .
P∆ABC =6. Найти S∆ABC
В
С
А
O

Слайд 11Повторение
Если в треугольник вписана окружность, то площадь треугольника равна произведению
полупериметра треугольника на радиус вписанной окружности
Вписанной в треугольник окружностью называется
окружность, которая касается всех сторон треугольника

Слайд 12Модуль «ГЕОМЕТРИЯ» №11
Ответ: .
Найти S∆ABC
В
А
D
С
8
5

Слайд 13Повторение
Площадь параллелограмма равна произведению двух сторон на синус угла между
ними
Сумма квадратов синуса и косинуса одного и того же угла
равна единице

Слайд 14Модуль «ГЕОМЕТРИЯ» №11
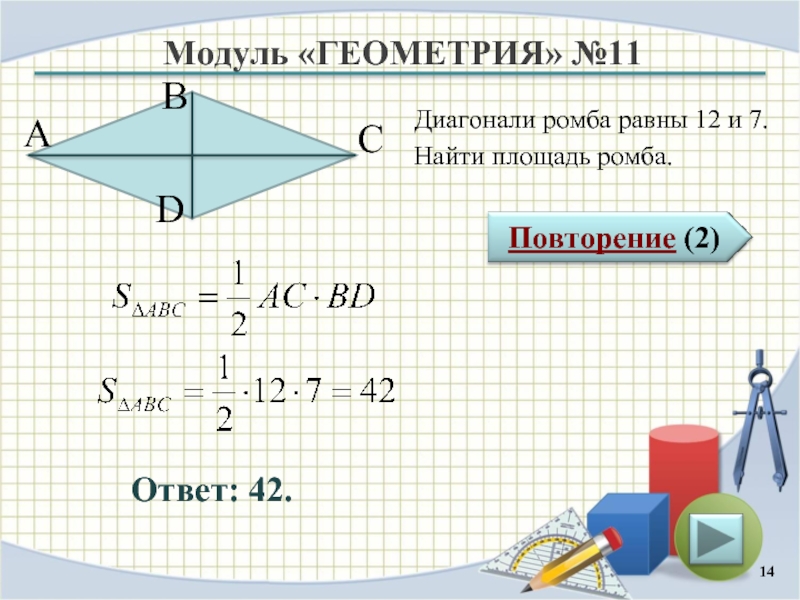
Ответ: 42.
Диагонали ромба равны 12 и 7.
Найти площадь
ромба.
В
А
D
С
Слайд 15Повторение
Площадь ромба равна половине произведения его диагоналей
Ромб – это параллелограмм
с равными сторонами

Слайд 16Модуль «ГЕОМЕТРИЯ» №11
Ответ: 73,5.
ABCD – трапеция. ВС в 2 раза
меньше AD. Найти площадь трапеции
В
А
D
С
14
H

Слайд 17Повторение
Площадь трапеции равна произведению полусуммы оснований на высоту
Трапеция – это
четырехугольник, две стороны которого параллельны

Слайд 18Модуль «ГЕОМЕТРИЯ» №11
Ответ: .
АС=10.
Найти площадь
прямоугольника
В
А
D
С
60⁰
О
АО=ВО=10:2=5
В ∆АОВ, где ∠ВАО=
∠АВО=(180⁰-60⁰):2=60⁰
⇒
По теореме Пифагора в ∆АВD

Слайд 19Повторение
Диагонали прямоугольника равны и делятся точкой пересечения пополам
В равнобедренном треугольнике
углы при основании равны
Если угол разбит на части, то его
градусная мера равна сумме его частей
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Площадь прямоугольника равна произведению соседних сторон

Слайд 20Модуль «ГЕОМЕТРИЯ» №11
Ответ: .
ABCD –
равнобедренная трапеция MK=8, боковая сторона равна 5.
Найти площадь трапеции.
В
А
D
С
8
135⁰
H
К
М
⇒
По теореме Пифагора в ∆АВH, где AH=BH=х
⇒
⇒

Слайд 21Повторение
Площадь трапеции равна произведению полусуммы оснований на высоту
Средняя линия трапеции
равна полусумме оснований
Если в прямоугольном треугольнике острый угол равен 45⁰,
то и другой острый угол равен 45⁰
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Слайд 22Модуль «ГЕОМЕТРИЯ» №11
Ответ: 168.
P∆ABC =98. Найти S∆ABC
В
С
А
25
H
АВ=P∆ABC –2ВС=98–2∙25=48
Т.к. ∆АВС равнобедренный, то
АH=HB=48:2=24
По теореме Пифагора в ∆АСH

Слайд 23Повторение
Периметр треугольника – это сумма длин сторон треугольника
Высота в равнобедренном
треугольнике, проведенная к основанию является медианой
В прямоугольном треугольнике квадрат гипотенузы
равен сумме квадратов катетов
Площадь треугольника равна половине произведения основания на высоту

Слайд 24Модуль «ГЕОМЕТРИЯ» №11
Ответ: 9.
В прямоугольном треугольнике высота, проведенная из вершины
прямого угла, равна медиане, проведенной из того же угла, АВ=6.
Найти S∆ABC
В
С
А
H
Если высота треугольника равна медиане, то ∆АВС – равнобедренный с основанием АВ
⇒
∠А=∠В=45⁰
∆HBC прямоугольный и равнобедренный, так как∠В=45⁰
⇒
CH=HВ=AB:2=3

Слайд 25Повторение
Если высота треугольника является и медианой, то такой треугольник равнобедренный
Если
прямоугольный треугольник равнобедренный, то его острые углы равны 45⁰
В прямоугольном
треугольнике квадрат гипотенузы равен сумме квадратов катетов
Площадь треугольника равна половине произведения основания на высоту

Слайд 26Модуль «ГЕОМЕТРИЯ» №11
Ответ: .
Найти S∆ABC
В
С
А
6
H
⇒
⇒
Т.к.∆АBC равнобедренный, то AH
– медиана
⇒
BC=2BH=
По теореме Пифагора в ∆АВH

Слайд 27Повторение
Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к
гипотенузе
Высота прямоугольного треугольника, проведенная к основанию, является медианой
В прямоугольном треугольнике
квадрат гипотенузы равен сумме квадратов катетов
Площадь треугольника равна половине произведения основания на высоту

Слайд 28Модуль «ГЕОМЕТРИЯ» №11
Ответ: 90.
Четырехугольник АВСD описан около четырехугольника, радиуса 4,5.
Найти S∆ABCD.
В
А
D
С
5
15
4,5
О
Соединим центр окружности с вершинами четырехугольника
Получим треугольники, высоты которых равны радиусу окружности
AB+DC=AD+BC
⇒
S∆AОB +S∆BOC =S∆COD +S∆AOD
⇒

Слайд 29Повторение
Если в четырехугольник можно вписать окружность, то суммы противоположных сторон
четырехугольника равны
Если фигура разбита на части, то площадь фигуры равна
сумме площадей ее частей
Радиус, проведенный в точку касания перпендикулярен касательной
Площадь треугольника равна половине произведения основания на высоту

Слайд 30Модуль «ГЕОМЕТРИЯ» №11
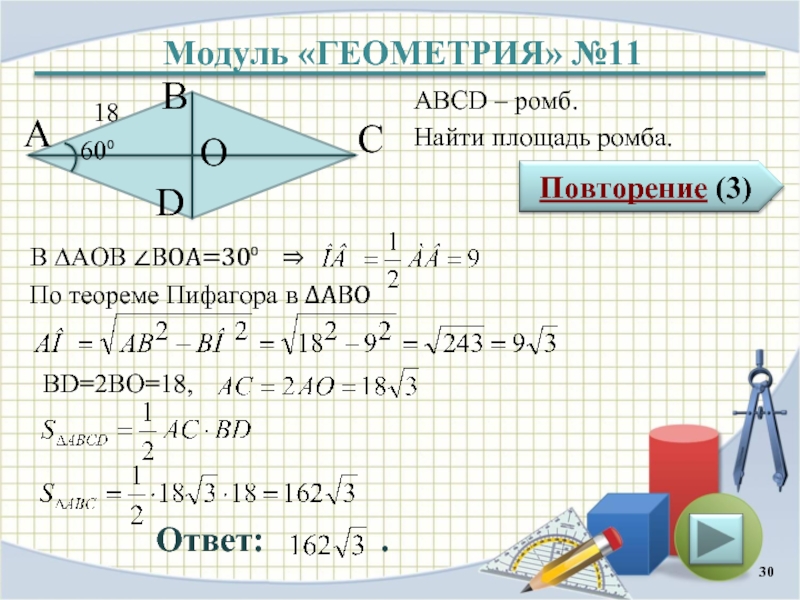
Ответ: .
ABCD
– ромб.
Найти площадь ромба.
В
А
D
С
60⁰
18
O
В ∆АОB ∠ВОА=30⁰
⇒
По теореме Пифагора в ∆АВО
BD=2BO=18,
Слайд 31Повторение
Диагонали ромба перпендикулярны и делят углы ромба пополам
В прямоугольном треугольнике
квадрат гипотенузы равен сумме квадратов катетов
Площадь ромба равна половине произведения
его диагоналей

Слайд 32Модуль «ГЕОМЕТРИЯ» №11
Ответ: 12.
Найти площадь параллелограмма
В
А
D
С
5
4
3
В
А
D
С
5
4
3
Так как ∆АВС – прямоугольный, то параллелограмм трансформируется в прямоугольник

Слайд 33Повторение
Треугольник, в котором стороны равны 3,4,5 называется Пифагоровым (т.е. треугольник
является прямоугольным)
Площадь прямоугольника равна произведению его измерений

Слайд 34Модуль «ГЕОМЕТРИЯ» №11
Ответ: 192π .
Дуга сектора равна 8π. Найти площадь
сектора.
30⁰
O
А
В
Сокр.=360⁰:30⁰∙ 8π=96π
Сокр.=2πr
⇒

Слайд 35Повторение
Длина окружности равна удвоенному произведению числа π на радиус окружности
Площадь
кругового сектора
вычисляется по формуле

Слайд 36Модуль «ГЕОМЕТРИЯ» №11
Ответ: .
Найти площадь кольца
3
5
⇒

Слайд 37Повторение
Площадь круга равна произведению числа π на квадрат радиуса круга
Если
фигура разделена на части, то его площадь равна сумме площадей
его частей

Слайд 38Модуль «ГЕОМЕТРИЯ» №11
Ответ: .
Найти площадь круга,
вписанного в равносторонний треугольник
В
С
А
⇒
⇒

Слайд 39Повторение
Сторона правильного треугольника, в который вписана окружность, равна
Радиусы вписанной
и описанной окружности около правильного многоугольника связаны
формулой
Площадь круга равна
произведению числа π на квадрат радиуса круга

Слайд 40Модуль «ГЕОМЕТРИЯ» №11
Ответ: .
Найти площадь круга, вписанного
в квадрат со стороной 18.
18
⇒
⇒

Слайд 41Повторение
Сторона правильного четырехугольника, в который вписана окружность, равна
Радиусы вписанной
и описанной окружности около правильного многоугольника связаны
формулой
Площадь круга равна
произведению числа π на квадрат радиуса круга

Слайд 42Использованные ресурсы
Автор шаблона: Ранько Елена Алексеевна учитель начальных классов МАОУ
лицей №21 г.Иваново http://www.uchportal.ru/load/160-1-0-31926http://www.uchportal.ru/load/160-1-0-31926е
«ГИА-2013. Математика: типовые экзаменационные варианты:
30 вариантов» под редакцией А. Л. Семенова, И. В. Ященко. – М.: Изд. «Национальное образование», 2013.

Площадь треугольника
Задача
1. В
треугольнике одна из сторон равна 27, а опущенная на нее высота – 11. Найдите
площадь треугольника.
Решение: Площадь треугольника = ½
основания*высоту
Пл.треугольника
= ½*27*11=148,5
Ответ:
148,5
Задача
2. Два
катета прямоугольного треугольника равны 4 и 9. Найдите площадь этого
треугольника.
Решение:
Пл.прямоугольного
треуг. = половине произведения катетов.
Пл.прямоуг.треуг.=(4*9):2=36:2=18
Ответ: 18
Задача
3. Периметр
равнобедренного треугольника равен 144, а основание – 64. Найдите площадь
треугольника.
Решение:
1) Т.к.
Треугольник равнобедренный, из этого следует, что две стороны равны АС=СВ,
найдем длину этих 
АС=СВ=(144-64):2=40.
2)
Формула Герона:
Найдем
полупериметр, т.к. периметр = 144, то полупериметр = 144:2=72.
Ответ: 768
Задача
4. Найдите
площадь треугольника.
Решение: Для формулы нам необходимо
знать основание и высоту
Основание=32+11=43.
Высота
= 60.
S треуг.= ½*60*43=1290
Ответ: 1290
32+11=43
Задача
5.
 |
6
3
Решение:
Задачу
можно решить по формуле Пика, можно по формуле площади треугольника.
Считаем
по клеточкам основание =3, высота = 6.
S=1/2*3*6= 9
Ответ: 9
Задачи
для самостоятельного решения:
1)
В
треугольнике одна из сторон равна 14, а опущенная на нее высота – 31. Найдите
площадь треугольника.
2)
Сторона
треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите
площадь этого треугольника.
3)
Два катета прямоугольного треугольника равны 7 и 12. Найдите площадь этого
треугольника.
4) Два катета
прямоугольного треугольника равны 18 и 7. Найдите площадь этого треугольника.
5) Периметр
равнобедренного треугольника равен 162, а основание – 72. Найдите площадь
треугольника.
6) Найдите площадь
треугольника
7) Найдите площадь
треугольника

9) Найдите площадь треугольника
10)
11) 
12)
13)
14)
16)
Проверить решение можно по ссылке:
https://onlinetestpad.com/hnl6ukjjcnpgo
Площадь треугольника требуется уметь находить, чтобы успешно решить модуль “Геометрия” в ОГЭ. Умение находить площадь треугольника является одним из основополагающих умений в геометрии. Для того, чтобы находить площадь треугольника в заданиях ОГЭ – нужно иметь представления о том, по каким формулам вообще находится площадь треугольника. Ниже мы приводим их все, а также даем анализ того, как часто встретятся вам эти формулы при выполнении заданий по геометрии в ОГЭ.
Задачи самые разнообразные, как и треугольники, как и методы их решения. Однако, для того, чтобы решать такие задачи, нам понадобятся формулы и общие сведения.
Площадь треугольника. Формулы. Задачи.
1. Формула нахождения площади треугольника по двум сторонам и углу между ними
Эта формула считается общей, ее очень часто используют, особенно если в треугольнике известен какой-либо угол. Ее кратко называют так “площадь треугольника через синус”. Итак, посмотрите на чертеж – нам дан треугольник ABC, известны две его стороны и угол между ними. Тогда площадь треугольника находится по формуле:
 Задачи на определение площади треугольника при заданных сторонах треугольника и углу между ними.
Задачи на определение площади треугольника при заданных сторонах треугольника и углу между ними.
Задача 1. Найдите площадь треугольника, две стороны которого равны 19 и 18, а угол между ними равен 300. Решение. Используем формулу площади треугольника через синус: Ответ: 85,5 Задача 2. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150 0 . Боковая сторона треугольника равна 2. Найдите площадь этого треугольника. Решение. Нарисуем треугольник. Обозначим его вершины – A, B, C. Значит, нам дано: <ABC=1500. AB=BC=2. Тогда для того, чтобы найти площадь треугольника, воспользуемся формулой нахождения площади треугольника по двум сторонам и углу между ними:

Ответ: 1.
2. Площадь треугольника через высоту.
Самая любимая школьниками формула определения площади треугольника – определение площади через высоту. В этой формуле всего нужно знать две величины – основание треугольника и высоту проведенную из вершины треугольника к этому основанию – смотрите рисунок.
Очень удобная формула для определения любого треугольника, если известны любые три его размера.
3. Площадь равнобедренного треугольника.
Равнобедренным называется треугольник, у которого две стороны равны. Нахождение площади равнобедренного треугольника ничем не отличается от нахождения площади обыкновенного треугольника, разве что формула площади равнобедренного треугольника несколько упрощается. Например, если дана боковая сторона треугольника и угол при вершине, то формула нахождения площади будет выглядеть так:
Вообще говоря, нет необходимости выводить и тем более запоминать некую мифическую формулу площади равнобедренного треугольника. Нужно просто помнить, что равнобедренный треугольник всего лишь частный случай общего, обыкновенного треугольника и все те формулы, которые применимы для нахождения площади треугольника, будут применимы и для равнобедренного треугольника.
Гораздо важнее не забыть свойства равнобедренного треугольника – высота (перпендикуляр), проведенная к основанию равнобедренного треугольника, есть медиана (делит основание пополам), биссектриса (делит угол напротив основания пополам). Углы при основании равнобедренного треугольника равны.
4. Площадь треугольника по координатам вершин
Никакой волшебной формулы тут нет – вы просто, используя координаты вершин, находите длины сторон треугольника, а затем подставляете их в формулу Герона.
5. Формула Герона для нахождения площади треугольника
,
где p – полупериметр треугольника, который находится по формуле:
а, b и c – стороны треугольника.
Таким образом, зная формулы, найти площадь треугольника не составит никакого труда.
Как находить площадь треугольника в заданиях ОГЭ.
В заданиях ОГЭ обычно площадь треугольника просят найти с помощью самой простой формулы – через основание и высоту.
Очень и очень редко встречается задача нахождения площади треугольника через две стороны и синус угла между ними, а уж формула Герона вообще не встречается, разве что вы можете ее использовать, если она вам очень нравится, да и то – в задачах второй части ОГЭ.
Площадь треугольника в заданиях ОГЭ
Площадь треугольника требуется уметь находить, чтобы успешно решить модуль «Геометрия» в ОГЭ. Умение находить площадь треугольника является одним из основополагающих умений в геометрии. Для того, чтобы находить площадь треугольника в заданиях ОГЭ — нужно иметь представления о том, по каким формулам вообще находится площадь треугольника. Ниже мы приводим их все, а также даем анализ того, как часто встретятся вам эти формулы при выполнении заданий по геометрии в ОГЭ.
Задачи самые разнообразные, как и треугольники, как и методы их решения. Однако, для того, чтобы решать такие задачи, нам понадобятся формулы и общие сведения.
Площадь треугольника. Формулы. Задачи.
1. Формула нахождения площади треугольника по двум сторонам и углу между ними
Эта формула считается общей, ее очень часто используют, особенно если в треугольнике известен какой-либо угол. Ее кратко называют так «площадь треугольника через синус». Итак, посмотрите на чертеж — нам дан треугольник ABC, известны две его стороны и угол между ними. Тогда площадь треугольника находится по формуле:
Задачи на определение площади треугольника при заданных сторонах треугольника и углу между ними.
Задача 1. Найдите площадь треугольника, две стороны которого равны 19 и 18, а угол между ними равен 30 0 . Решение. Используем формулу площади треугольника через синус: Ответ: 85,5 Задача 2. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150 0 . Боковая сторона треугольника равна 2. Найдите площадь этого треугольника. Решение. Нарисуем треугольник. Обозначим его вершины — A, B, C. Значит, нам дано: 0 . AB=BC=2. Тогда для того, чтобы найти площадь треугольника, воспользуемся формулой нахождения площади треугольника по двум сторонам и углу между ними:
В этой задаче мы применили метод приведения для тригонометрических функций.
2. Площадь треугольника через высоту.
Самая любимая школьниками формула определения площади треугольника — определение площади через высоту. В этой формуле всего нужно знать две величины — основание треугольника и высоту проведенную из вершины треугольника к этому основанию — смотрите рисунок.
Очень удобная формула для определения любого треугольника, если известны любые три его размера.
3. Площадь равнобедренного треугольника.
Равнобедренным называется треугольник, у которого две стороны равны. Нахождение площади равнобедренного треугольника ничем не отличается от нахождения площади обыкновенного треугольника, разве что формула площади равнобедренного треугольника несколько упрощается. Например, если дана боковая сторона треугольника и угол при вершине, то формула нахождения площади будет выглядеть так:
Вообще говоря, нет необходимости выводить и тем более запоминать некую мифическую формулу площади равнобедренного треугольника. Нужно просто помнить, что равнобедренный треугольник всего лишь частный случай общего, обыкновенного треугольника и все те формулы, которые применимы для нахождения площади треугольника, будут применимы и для равнобедренного треугольника.
Гораздо важнее не забыть свойства равнобедренного треугольника — высота (перпендикуляр), проведенная к основанию равнобедренного треугольника, есть медиана (делит основание пополам), биссектриса (делит угол напротив основания пополам). Углы при основании равнобедренного треугольника равны.
4. Площадь треугольника по координатам вершин
Никакой волшебной формулы тут нет — вы просто, используя координаты вершин, находите длины сторон треугольника, а затем подставляете их в формулу Герона.
5. Формула Герона для нахождения площади треугольника
Таким образом, зная формулы, найти площадь треугольника не составит никакого труда.
Как находить площадь треугольника в заданиях ОГЭ.
В заданиях ОГЭ обычно площадь треугольника просят найти с помощью самой простой формулы — через основание и высоту.
Очень и очень редко встречается задача нахождения площади треугольника через две стороны и синус угла между ними, а уж формула Герона вообще не встречается, разве что вы можете ее использовать, если она вам очень нравится, да и то — в задачах второй части ОГЭ.
Найти площадь треугольника гиа
В треугольнике одна из сторон равна 10, а опущенная на нее высота — 5. Найдите площадь треугольника.
Площадь треугольника равна половине произведения высоты на основание. Таким образом:
В треугольнике одна из сторон равна 10, другая равна , а угол между ними равен 60°. Найдите площадь треугольника.
Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:
Найдите площадь треугольника, изображённого на рисунке.
Заметим, что треугольник со сторонами 24, 32 и 40 подобен египетскому треугольнику со сторонами 3, 4, 5 с коэффициентом 8. Следовательно, этот треугольник прямоугольный, а отрезок длины 24 — высота изображенного на рисунке треугольника. Тогда его площадь можно найти как половину произведения основания на высоту:
В треугольнике ABC отрезок DE — средняя линия. Площадь треугольника CDE равна 97. Найдите площадь треугольника ABC.
Треугольники ABC и DEC подобны по двум углам. Коэффициент подобия k = 2, так как Значит,
На стороне AC треугольника ABC отмечена точка D так, что AD = 3, DC = 7. Площадь треугольника ABC равна 20. Найдите площадь треугольника BCD.
Площадь треугольника равняется половине произведения сторон на синус угла между ними: так как значит, поэтому
Выразим через площадь треугольника BCD:
Приведем другое решение.
Площадь треугольника равна половине произведения основания на высоту, следовательно, можно найти высоту треугольника ABC:
тогда
Треугольник BCD имеет такую же высоту, что и треугольник ABC, следовательно,
Приведем еще одно решение.
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
тогда
Материал для подготовки к ОГЭ по математике «Площадь треугольника»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Задача 1. В треугольнике одна из сторон равна 27, а опущенная на нее высота – 11. Найдите площадь треугольника.
Решение: Площадь треугольника = ½ основания*высоту
Задача 2. Два катета прямоугольного треугольника равны 4 и 9. Найдите площадь этого треугольника.
Решение: Пл.прямоугольного треуг. = половине произведения катетов.
Задача 3. Периметр равнобедренного треугольника равен 144, а основание – 64. Найдите площадь треугольника.
1) Т.к. Треугольник равнобедренный, из этого следует, что две стороны равны АС=СВ, найдем длину этих сторон:
2) Формула Герона:
Найдем полупериметр, т.к. периметр = 144, то полупериметр = 144:2=72.
Задача 4. Найдите площадь треугольника.
Решение: Для формулы нам необходимо знать основание и высоту
S треуг.= ½*60*43=1290
Задачу можно решить по формуле Пика, можно по формуле площади треугольника.
Считаем по клеточкам основание =3, высота = 6.
Задачи для самостоятельного решения:
1) В треугольнике одна из сторон равна 14, а опущенная на нее высота – 31. Найдите площадь треугольника.
2) Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника.
3) Два катета прямоугольного треугольника равны 7 и 12. Найдите площадь этого треугольника.
4) Два катета прямоугольного треугольника равны 18 и 7. Найдите площадь этого треугольника.
5) Периметр равнобедренного треугольника равен 162, а основание – 72. Найдите площадь треугольника.
6) Найдите площадь треугольника
7) Найдите площадь треугольника

9) Найдите площадь треугольника
10)
11)
12)
13)
14)
16)
Проверить решение можно по ссылке:
Краткое описание документа:
Цель: систематизировать знания учащихся по ключевым разделам планиметрии; создать содержательные и организационные условия для применения школьниками комплекса знаний для решения задач, включаемых в материалы ОГЭ.
В материале по подготовке к ОГЭ приведены алгоритмы решения задач на тему «Площадь треугольника», основные формулы нахождения площади треугольника, задачи для самостоятельного решения, возможность проверки заданий он-лайн.
Курс повышения квалификации
Охрана труда
- Сейчас обучается 98 человек из 44 регионов
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
- Сейчас обучается 349 человек из 64 регионов
Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 216 человек из 53 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 536 328 материалов в базе
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 08.08.2019
- 269
- 0
- 08.08.2019
- 396
- 1
- 08.08.2019
- 217
- 0
- 08.08.2019
- 120
- 0
- 08.08.2019
- 212
- 0
- 08.08.2019
- 259
- 4
- 08.08.2019
- 163
- 0
- 08.08.2019
- 2935
- 11
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 08.08.2019 4163
- DOCX 1.1 мбайт
- 300 скачиваний
- Рейтинг: 4 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Бутусина Галина Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 3 месяца
- Подписчики: 0
- Всего просмотров: 8752
- Всего материалов: 6
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид
Время чтения: 1 минута
Ученики 5-11 классов Воронежа перейдут на дистанционное обучение с 3 февраля
Время чтения: 1 минута
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
В Самаре и Тольятти часть школьников перевели на дистанционное обучение
Время чтения: 1 минута
Путин поручил обучать педагогов работе с девиантным поведением
Время чтения: 1 минута
Минобрнауки учредит стипендию для студентов — победителей международных олимпиад
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
http://math-oge.sdamgia.ru/test?theme=40
http://infourok.ru/material-dlya-podgotovki-k-oge-po-matematike-ploschad-treugolnika-3806698.html
Задания на нахождение площади треугольника встречаются в основном среди задач с кратким ответом и не требуют подробного решения. Опять же, есть и задачи супер-простые, есть и довольно сложные.
Вспомним, что площадь треугольника можно найти несколькими способами.
1) S = 1/2 ahа, где а — сторона, hа — высота к этой стороне. Высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону. В прямоугольном треугольнике катеты являются высотами друг к другу.
2) S = 1/2 ab sinγ , a и b — стороны, γ — угол между ними.
Эти формулы будут у вас в справочных материалах на ОГЭ. Но есть такие, которых в справочнике не будет, а через них решать подобные задания проще и быстрее. Поэтому, повторите тему о подобии треугольников (признаки подобия; площади подобных треугольников относятся как квадраты их соответственных сторон). Еще нужно вспомнить, что если треугольники имеют общую вершину, а их основания лежат на одной прямой, то отношение их площадей равно отношению их оснований.
Открытый банк заданий ФИПИ располагает следующими заданиями, которые могут попасться вам на реальном экзамене в этом году.
Реальные задания по геометрии из банка ФИПИ
На стороне AC треугольника ABC отмечена точка D так, что AD=3, DC=7. Площадь треугольника ABC равна 20. Найдите площадь треугольника BCD.
Решение:
Для вычисления площади треугольника существует несколько формул. Ни для одной из них у нас не хватает данных. Значит недостающие данные надо получить.
1 способ
Посмотрим, что общее есть у треугольников ABC и BCD:
1. Сторона BC
2. Угол BCD.
Воспользуемся формулой «через две стороны и угол между ними».Площадь треугольника ABC равняется половине произведения сторон на синус угла между ними:
SABC=1/2*AC*BC*sinC
Так как АС = АD + DС, то
SABC=1/2*(AD+DC)*BC*sinC, поэтому
BC*sinC=$frac{S_{ABC}}{displaystylefrac12ast(AD+DC)}=frac{20}{{displaystylefrac12}ast(3+7)}=4$Выразим площадь треугольника BCD через sinC:
SBCD=1/2*DC*BC*sinC
Подставляем значение BC*sinC, полученное ранее, и значение DC, известное из условия:
SBCD=1/2*7*4
SBCD=14Ответ: 14
2 способ
Площадь треугольника равна половине произведения основания на высоту, следовательно, можно найти высоту треугольника ABC:
SАВС=1/2 АС*h
а так как АС = АD + DС, то
SАВС=1/2 (АD + DС)*h
$h=frac{2S_{АВС}}{АD+DС}=frac{2ast20}{3+7}=4$Треугольник BCD имеет такую же высоту, что и треугольник ABC, значит,
SВСD=1/2 DС*h = 1/2 * 7 * 4 = 14
Ответ: 14
3 способ (самый короткий)
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 3 + 7 = 10
SВСD = 20 * 7 / 10 = 14Ответ: 14
4F1471
На стороне AC треугольника ABC отмечена точка D так, что AD=6, DC=10. Площадь треугольника ABC равна 48. Найдите площадь треугольника BCD.
Решение:
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 6 + 10 = 16
SВСD = 48 * 10 / 16 = 30Ответ: 30
214ED6
На стороне AC треугольника ABC отмечена точка D так, что AD=4, DC=8. Площадь треугольника ABC равна 36. Найдите площадь треугольника BCD.
Решение:
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 4 + 8 = 12
SВСD = 36 * 8 / 12 = 24Ответ: 24
E88B4B
На стороне AC треугольника ABC отмечена точка D так, что AD=2, DC=7. Площадь треугольника ABC равна 27. Найдите площадь треугольника BCD.
Решение:
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 2 + 7 = 9
SВСD = 27 * 7 / 9 = 21Ответ: 21
972236
На стороне AC треугольника ABC отмечена точка D так, что AD=5, DC=9. Площадь треугольника ABC равна 56. Найдите площадь треугольника BCD.
Решение:
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 5 + 9 = 14
SВСD = 56 * 9 / 14 = 36Ответ: 36
BC4593
На стороне AC треугольника ABC отмечена точка D так, что AD=4, DC=7. Площадь треугольника ABC равна 55. Найдите площадь треугольника ABD.
Решение:
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 4 + 7 = 11
SВСD = 55 * 7 / 11 = 35Ответ: 35
258E9A
На стороне AC треугольника ABC отмечена точка D так, что AD=3, DC=10. Площадь треугольника ABC равна 39. Найдите площадь треугольника ABD.
Решение:
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 3 + 10 = 13
SВСD = 39 * 10 / 13 = 30Ответ: 30
4065B0
На стороне AC треугольника ABC отмечена точка D так, что AD=6, DC=8. Площадь треугольника ABC равна 42. Найдите площадь треугольника ABD.
Решение:
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 6 + 8 = 14
SВСD = 42 * 8 / 14 = 24Ответ: 24
B4CAE7
На стороне AC треугольника ABC отмечена точка D так, что AD=5, DC=7. Площадь треугольника ABC равна 60. Найдите площадь треугольника ABD.
Решение:
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 5 + 7 = 12
SВСD = 60 * 7 / 12 = 35Ответ: 35
F63DA7
На стороне AC треугольника ABC отмечена точка D так, что AD=2, DC=13. Площадь треугольника ABC равна 75. Найдите площадь треугольника ABD.
Решение:
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 2 + 13 = 15
SВСD = 75 * 13 / 15 = 65Ответ: 65
0D7C95
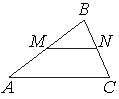
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=18, MN=8. Площадь треугольника ABC равна 81. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$frac{S_{MNB}}{S_{ABC}}=left(frac{MN}{AC}right)^2$ , ⇒
$S_{MNB}=left(frac{MN}{AC}right)^2ast S_{ABC}$
SMNB = (8/18)2 * 81 = 64 * 81 /324 = 16
Ответ: 16
8EBCEB
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=21, MN=14. Площадь треугольника ABC равна 27. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$frac{S_{MNB}}{S_{ABC}}=left(frac{MN}{AC}right)^2$ , поэтому
$S_{MNB}=left(frac{MN}{AC}right)^2ast S_{ABC}$
SMNB = (14/21)2 * 27 = 12
Ответ: 12
DABB4F
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=24, MN=18. Площадь треугольника ABC равна 48. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$frac{S_{MNB}}{S_{ABC}}=left(frac{MN}{AC}right)^2$ , поэтому
$S_{MNB}=left(frac{MN}{AC}right)^2ast S_{ABC}$
SMNB = (18/24)2 * 48 = 27
Ответ: 27
F8DE6C
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=27, MN=18. Площадь треугольника ABC равна 63. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$frac{S_{MNB}}{S_{ABC}}=left(frac{MN}{AC}right)^2$ , поэтому
$S_{MNB}=left(frac{MN}{AC}right)^2ast S_{ABC}$
SMNB = (18/27)2 * 63 = 28
Ответ: 28
BB979E
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=30, MN=12. Площадь треугольника ABC равна 25. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$frac{S_{MNB}}{S_{ABC}}=left(frac{MN}{AC}right)^2$ , поэтому
$S_{MNB}=left(frac{MN}{AC}right)^2ast S_{ABC}$
SMNB = (12/30)2 * 25 = 4
Ответ: 4
4CC815
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=16, MN=12. Площадь треугольника ABC равна 80. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$frac{S_{MNB}}{S_{ABC}}=left(frac{MN}{AC}right)^2$ , поэтому
$S_{MNB}=left(frac{MN}{AC}right)^2ast S_{ABC}$
SMNB = (12/16)2 * 80 = 45
Ответ: 45
9ACF8B
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=27. Площадь треугольника ABC равна 96. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$frac{S_{MNB}}{S_{ABC}}=left(frac{MN}{AC}right)^2$ , поэтому
$S_{MNB}=left(frac{MN}{AC}right)^2ast S_{ABC}$
SMNB = (27/36)2 * 96 = 54
Ответ: 54
9C5C4D
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=48, MN=40. Площадь треугольника ABC равна 72. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$frac{S_{MNB}}{S_{ABC}}=left(frac{MN}{AC}right)^2$ , поэтому
$S_{MNB}=left(frac{MN}{AC}right)^2ast S_{ABC}$
SMNB = (40/48)2 * 72 = 50
Ответ: 50
51F110
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=44, MN=24. Площадь треугольника ABC равна 121. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$frac{S_{MNB}}{S_{ABC}}=left(frac{MN}{AC}right)^2$ , поэтому
$S_{MNB}=left(frac{MN}{AC}right)^2ast S_{ABC}$
SMNB = (24/44)2 * 121 = 36
Ответ: 36
A1451C
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=28. Площадь треугольника ABC равна 162. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$frac{S_{MNB}}{S_{ABC}}=left(frac{MN}{AC}right)^2$ , поэтому
$S_{MNB}=left(frac{MN}{AC}right)^2ast S_{ABC}$
SMNB = (28/36)2 * 162 = 98
Ответ: 98
22636E
Два катета прямоугольного треугольника равны 6 и 7. Найдите площадь этого треугольника.
Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 6 * 7 = 21Ответ: 21
F594AC
Два катета прямоугольного треугольника равны 9 и 6. Найдите площадь этого треугольника.
Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 9 * 6 = 27Ответ: 27
0DA313
Два катета прямоугольного треугольника равны 4 и 11. Найдите площадь этого треугольника.
Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 4 * 11 = 22Ответ: 22
1E12D2
Два катета прямоугольного треугольника равны 14 и 5. Найдите площадь этого треугольника.
Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 14 * 5 = 35Ответ: 35
201E89
Два катета прямоугольного треугольника равны 6 и 13. Найдите площадь этого треугольника.
Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 6 * 13 = 39Ответ: 39
9C5CE2
Два катета прямоугольного треугольника равны 4 и 9. Найдите площадь этого треугольника.
Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 4 * 9 = 18Ответ: 18
916443
Два катета прямоугольного треугольника равны 11 и 6. Найдите площадь этого треугольника.
Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 11 * 6 = 33Ответ: 33
1276A8
Два катета прямоугольного треугольника равны 4 и 10. Найдите площадь этого треугольника.
Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 4 * 10 = 20Ответ: 20
F6B402
Два катета прямоугольного треугольника равны 13 и 4. Найдите площадь этого треугольника.
Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 13 * 4 = 26Ответ: 26
5F6CB3
Два катета прямоугольного треугольника равны 7 и 12. Найдите площадь этого треугольника.
Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 7 * 12 = 42Ответ: 42
C10B89
Два катета прямоугольного треугольника равны 12 и 5. Найдите площадь этого треугольника.
Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 12 * 5 = 30Ответ: 30
160CE6
Два катета прямоугольного треугольника равны 18 и 7. Найдите площадь этого треугольника.
Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 18 * 7 = 63Ответ: 63
5E7907
Сторона треугольника равна 14, а высота, проведённая к этой стороне, равна 31. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 14 *31 = 217
Ответ: 217
8582E2
Сторона треугольника равна 24, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 24 * 19 = 228
Ответ: 228
43135F
Сторона треугольника равна 18, а высота, проведённая к этой стороне, равна 17. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 18 * 17 = 153
Ответ: 153
33F315
Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 16 * 19 = 152
Ответ: 152
7A4858
Сторона треугольника равна 14, а высота, проведённая к этой стороне, равна 23. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 14 * 23 = 161
Ответ: 161
CB2956
Сторона треугольника равна 29, а высота, проведённая к этой стороне, равна 12. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 29 * 12 = 174
Ответ: 174
8993A6
Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 27. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 16 * 27 = 216
Ответ: 216
DC9E1D
Сторона треугольника равна 12, а высота, проведённая к этой стороне, равна 33. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 12 * 33 = 198
Ответ: 198
22C21A
Сторона треугольника равна 18, а высота, проведённая к этой стороне, равна 22. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 18 * 22 = 198
Ответ: 198
B45622
Сторона треугольника равна 8, а высота, проведённая к этой стороне, равна 31. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 8 * 31 = 124
Ответ: 124
C15599
Периметр треугольника равен 50, одна из сторон равна 20, а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 50/2 * 4 = 100
Длина одной из сторон — лишние данные, игнорируем их.
Ответ: 100
099B7F
Периметр треугольника равен 48, одна из сторон равна 18, а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 48/2 * 3 = 72
Длина одной из сторон — лишние данные, игнорируем их.
Ответ: 72
691110
Периметр треугольника равен 71, одна из сторон равна 21, а радиус вписанной в него окружности равен 6. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 71/2 * 6 = 213
Длина одной из сторон — лишние данные, игнорируем их.
Ответ: 213
F93971
Периметр треугольника равен 56, одна из сторон равна 19, а радиус вписанной в него окружности равен 5. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 56/2 * 5 = 140
Длина одной из сторон — лишние данные, игнорируем их.
Ответ: 140
2E895A
Периметр треугольника равен 110, одна из сторон равна 38, а радиус вписанной в него окружности равен 10. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 110/2 * 10 = 550
Длина одной из сторон — лишние данные, игнорируем их.
Ответ: 550
A70D9B
Периметр треугольника равен 120, одна из сторон равна 40, а радиус вписанной в него окружности равен 7. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 120/2 * 7 = 420
Длина одной из сторон — лишние данные, игнорируем их.
Ответ: 420
569EAC
Периметр треугольника равен 140, одна из сторон равна 56, а радиус вписанной в него окружности равен 9. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 140/2 * 9 = 630
Длина одной из сторон — лишние данные, игнорируем их.
Ответ: 630
17E9C9
Периметр треугольника равен 60, одна из сторон равна 12, а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 60/2 * 3 = 90
Длина одной из сторон — лишние данные, игнорируем их.
Ответ: 90
B0D10B
Периметр треугольника равен 33, одна из сторон равна 7, а радиус вписанной в него окружности равен 2. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 33/2 * 2 = 33
Длина одной из сторон — лишние данные, игнорируем их.
Ответ: 33
65845E
Периметр треугольника равен 54, одна из сторон равна 15, а радиус вписанной в него окружности равен 1. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 54/2 * 1 = 27
Длина одной из сторон — лишние данные, игнорируем их.
Ответ: 27
239EF1
Площадь параллелограмма ABCD равна 68. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SABС = 68/2 = 34
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SEBC = 1/2 SABC = 1/2 * 34 = 17
Ответ: 17
795F61
Площадь параллелограмма ABCD равна 44. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SABС = 44/2 = 22
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SEBC = 1/2 SABC = 1/2 * 22 = 11
Ответ: 11
1ABE2A
Площадь параллелограмма ABCD равна 84. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SABС = 84/2 = 42
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SEBC = 1/2 SABC = 1/2 * 42 = 21
Ответ: 21
A6BEE2
Площадь параллелограмма ABCD равна 196. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SABС = 196/2 = 98
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SEBC = 1/2 SABC = 1/2 * 98 = 49
Ответ: 49
ADA977
Площадь параллелограмма ABCD равна 112. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SABС = 112/2 = 56
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SEBC = 1/2 SABC = 1/2 * 56 = 28
Ответ: 28
4DB6C1
Площадь параллелограмма ABCD равна 104. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SABС = 104/2 = 52
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SEBC = 1/2 SABC = 1/2 * 52 = 26
Ответ: 26
CDB192
Площадь параллелограмма ABCD равна 148. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SABС = 148/2 = 74
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SEBC = 1/2 SABC = 1/2 * 74 = 37
Ответ: 37
E2BFC0
Площадь параллелограмма ABCD равна 140. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SABС = 140/2 = 70
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SEBC = 1/2 SABC = 1/2 * 70 = 35
Ответ: 35
20E710
Площадь параллелограмма ABCD равна 136. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SABС = 136/2 = 68
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SEBC = 1/2 SABC = 1/2 * 68 = 34
Ответ: 34
2373D8















 Задачи на определение площади треугольника при заданных сторонах треугольника и углу между ними.
Задачи на определение площади треугольника при заданных сторонах треугольника и углу между ними.